 مشاهده در TensorFlow.org مشاهده در TensorFlow.org |  در Google Colab اجرا شود در Google Colab اجرا شود |  مشاهده منبع در GitHub مشاهده منبع در GitHub |  دانلود دفترچه یادداشت دانلود دفترچه یادداشت |
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
A [مفصل] (https://en.wikipedia.org/wiki/Copula_ (probability_theory 29٪) یک رویکرد کلاسیک برای گرفتن وابستگی بین متغیرهای تصادفی است. بیشتر به طور رسمی، یک مفصل یک توزیع چند متغیره است \(C(U_1, U_2, ...., U_n)\) به طوری که به حاشیه راندن می دهد \(U_i \sim \text{Uniform}(0, 1)\).
کوپولاها جالب هستند زیرا می توانیم از آنها برای ایجاد توزیع های چند متغیره با حاشیه های دلخواه استفاده کنیم. این دستور پخت است:
- با استفاده از انتگرال احتمال تبدیل نوبت خودسرانه RV مستمر \(X\) به لباس یک \(F_X(X)\)، که در آن \(F_X\) CDF است \(X\).
- با توجه به مفصل (مثلا دو متغیره) \(C(U, V)\)، ما که \(U\) و \(V\) دارای توزیع حاشیه ای یکنواخت.
- حالا با توجه به RV ما از علاقه \(X, Y\)، ایجاد یک جدید توزیع \(C'(X, Y) = C(F_X(X), F_Y(Y))\). حاشیه برای \(X\) و \(Y\) آنهایی را که ما مورد نظر است.
حاشیه ها تک متغیره هستند و بنابراین ممکن است اندازه گیری و/یا مدل سازی آسان تر باشد. یک کوپول شروع از حاشیه ها را امکان پذیر می کند و در عین حال به همبستگی دلخواه بین ابعاد نیز دست می یابد.
کوپولای گاوسی
برای نشان دادن نحوه ساخت کوپولا، موردی را در نظر بگیرید که وابستگی را با توجه به همبستگیهای گاوسی چند متغیره در نظر بگیرید. یک Gaussian مفصل است داده شده توسط \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) که در آن \(\Phi_\Sigma\) نشان دهنده CDF یک MultivariateNormal با کوواریانس \(\Sigma\) و متوسط 0، و \(\Phi^{-1}\) CDF معکوس برای استاندارد نرمال است.
اعمال CDF معکوس معمولی، ابعاد یکنواختی را که به طور معمول توزیع می شود، منحرف می کند. سپس با اعمال CDF نرمال چند متغیره، توزیع به صورت حاشیه ای یکنواخت و با همبستگی های گاوسی له می شود.
بنابراین، آنچه ما این است که گاوسی مفصل توزیع بیش واحد مربع است \([0, 1]^n\) با حاشیه یکنواخت.
تعریف به عنوان مثل، گاوسی مفصل را می توان با اجرا tfd.TransformedDistribution و مناسب Bijector . این است که، ما در حال تبدیل یک MultivariateNormal، از طریق استفاده از توزیع نرمال را معکوس CDF، اجرا شده توسط tfb.NormalCDF bijector.
در زیر، ما یک Gaussian مفصل پیاده سازی با یک فرض ساده: که کوواریانس است توسط یک عامل Cholesky (از این رو کوواریانس برای پارامتر MultivariateNormalTriL ). (یک نفر می تواند دیگر استفاده کنید tf.linalg.LinearOperators به رمز فرضیات رایگان ماتریس متفاوت است.).
class GaussianCopulaTriL(tfd.TransformedDistribution):
"""Takes a location, and lower triangular matrix for the Cholesky factor."""
def __init__(self, loc, scale_tril):
super(GaussianCopulaTriL, self).__init__(
distribution=tfd.MultivariateNormalTriL(
loc=loc,
scale_tril=scale_tril),
bijector=tfb.NormalCDF(),
validate_args=False,
name="GaussianCopulaTriLUniform")
# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
[x_grid[..., np.newaxis],
y_grid[..., np.newaxis]], axis=-1)
pdf = GaussianCopulaTriL(
loc=[0., 0.],
scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)
# Plot its density.
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
با این حال، قدرت چنین مدلی استفاده از تبدیل انتگرال احتمال، برای استفاده از کوپول در RV های دلخواه است. به این ترتیب، می توانیم حاشیه های دلخواه را مشخص کنیم و از کوپولا برای دوختن آنها به یکدیگر استفاده کنیم.
ما با یک مدل شروع می کنیم:
\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]
و با استفاده از مفصل به دست آوردن یک دو متغیره RV \(Z\)، که دارای حاشیه Kumaraswamy و گامبل .
ما با ترسیم توزیع محصول تولید شده توسط آن دو RV شروع خواهیم کرد.
a = 2.0
b = 2.0
gloc = 0.
gscale = 1.
x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)
# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)
pdf = x.prob(x_grid) * y.prob(y_grid)
# Plot its density
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
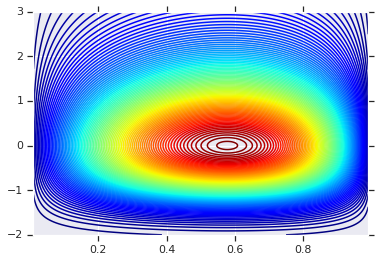
توزیع مشترک با حاشیه های مختلف
اکنون از یک کوپول گاوسی برای جفت کردن توزیع ها با هم استفاده می کنیم و آن را رسم می کنیم. دوباره ابزار ما را از انتخاب است TransformedDistribution استفاده از مناسب Bijector برای به دست آوردن حاشیه انتخاب شده است.
به طور خاص، ما یک با استفاده از Blockwise bijector که در بخش های مختلف بردار اعمال bijectors مختلف (که هنوز هم یک تغییر و تحول دوسویی).
حالا می توانیم Copula مورد نظر خود را تعریف کنیم. با توجه به لیستی از حاشیه های هدف (که به صورت بیژکتور کدگذاری می شوند)، می توانیم به راحتی توزیع جدیدی بسازیم که از کوپولا استفاده می کند و حاشیه های مشخص شده را دارد.
class WarpedGaussianCopula(tfd.TransformedDistribution):
"""Application of a Gaussian Copula on a list of target marginals.
This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
which are distributed marginally (with CDF) [F_0, ... F_n],
`GaussianCopula` represents an application of the Copula, such that the
resulting multivariate distribution has the above specified marginals.
The marginals are specified by `marginal_bijectors`: These are
bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.
block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
length should be same as length of `marginal_bijectors`.
See tfb.Blockwise for details
"""
def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
super(WarpedGaussianCopula, self).__init__(
distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
bijector=tfb.Blockwise(bijectors=marginal_bijectors,
block_sizes=block_sizes),
validate_args=False,
name="GaussianCopula")
در نهایت، اجازه دهید در واقع از این کوپولای گاوسی استفاده کنیم. ما یک Cholesky از استفاده \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\)، که به واریانس 1 مطابقت دارد، و ارتباط \(\rho\) برای چند متغیره طبیعی است.
چند مورد را بررسی می کنیم:
# Create our coordinates:
coordinates = np.concatenate(
[x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)
def create_gaussian_copula(correlation):
# Use Gaussian Copula to add dependence.
return WarpedGaussianCopula(
loc=[0., 0.],
scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
# These encode the marginals we want. In this case we want X_0 has
# Kumaraswamy marginal, and X_1 has Gumbel marginal.
marginal_bijectors=[
tfb.Invert(tfb.KumaraswamyCDF(a, b)),
tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])
# Note that the zero case will correspond to independent marginals!
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
copula = create_gaussian_copula(correlation)
copulas.append(copula)
probs.append(copula.prob(coordinates))
# Plot it's density
for correlation, copula_prob in zip(correlations, probs):
plt.figure()
plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
plt.title('Correlation {}'.format(correlation))
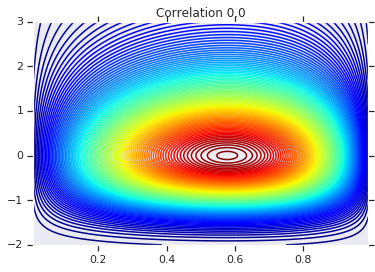
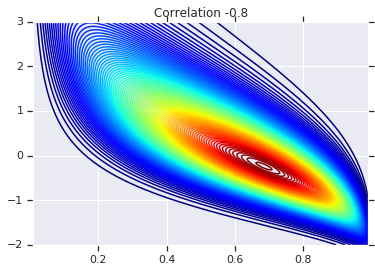
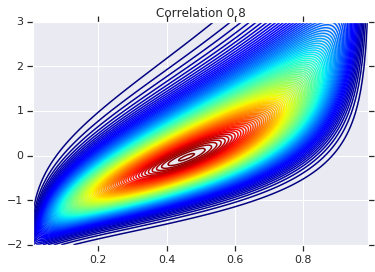
در نهایت، اجازه دهید بررسی کنیم که ما واقعاً حاشیههایی را که میخواهیم دریافت میکنیم.
def kumaraswamy_pdf(x):
return tfd.Kumaraswamy(a, b).prob(np.float32(x))
def gumbel_pdf(x):
return tfd.Gumbel(gloc, gscale).prob(np.float32(x))
copula_samples = []
for copula in copulas:
copula_samples.append(copula.sample(10000))
plot_rows = len(correlations)
plot_cols = 2 # for 2 densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))
# Let's marginalize out on each, and plot the samples.
for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
k = copula_sample[..., 0].numpy()
g = copula_sample[..., 1].numpy()
_, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))
_, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))
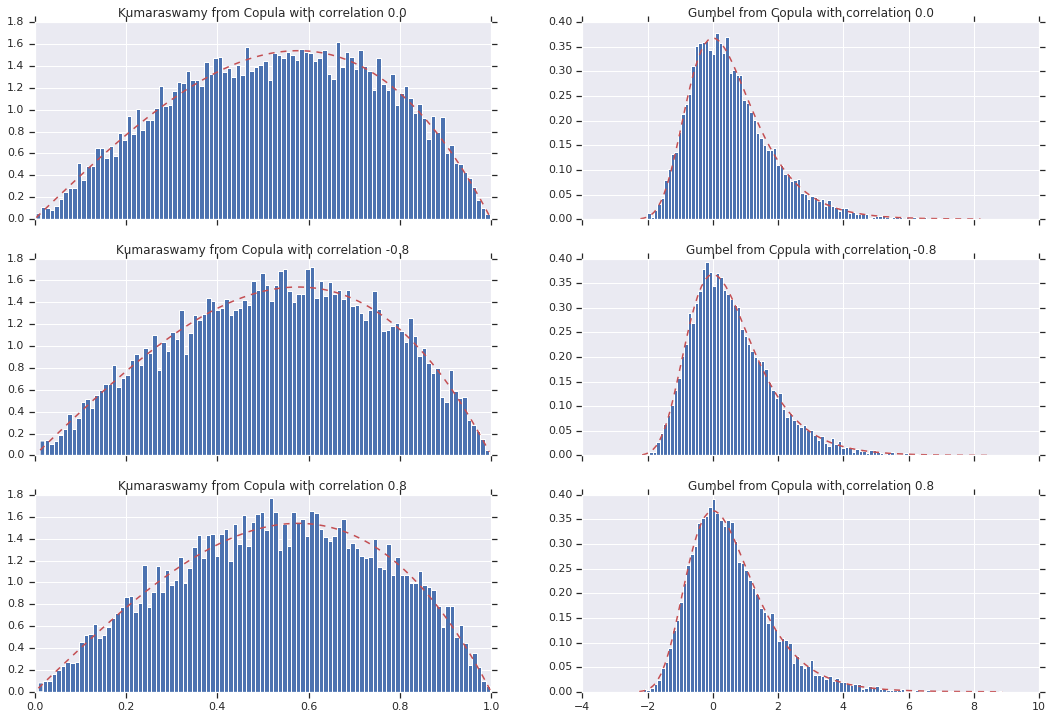
نتیجه
و ما به آنجا می رویم! ما نشان داده ایم که ما می توانیم گاوسی مفصل با استفاده از ساخت Bijector API.
به طور کلی، نوشتن bijectors با استفاده از Bijector API و آهنگسازی آنها را با یک توزیع، می توانید خانواده های ثروتمند توزیع برای مدل سازی انعطاف پذیر ایجاد کنید.
