 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
A [cópula] (https://en.wikipedia.org/wiki/Copula_ (% probability_theory 29) es un enfoque clásico para la captura de la dependencia entre variables aleatorias. Más formalmente, una cópula es una distribución multivariante \(C(U_1, U_2, ...., U_n)\) tal que marginación da \(U_i \sim \text{Uniform}(0, 1)\).
Las cópulas son interesantes porque las podemos usar para crear distribuciones multivariadas con marginales arbitrarias. Esta es la receta:
- Usando la Integral Probabilidad Transform vueltas una arbitraria RV continua \(X\) en un uniforme uno \(F_X(X)\), donde \(F_X\) es la CDF de \(X\).
- Dada una cópula (por ejemplo de dos variables) \(C(U, V)\), tenemos que \(U\) y \(V\) tienen distribuciones marginales uniformes.
- Ahora da nuestro RV es de interés \(X, Y\), crear una nueva distribución \(C'(X, Y) = C(F_X(X), F_Y(Y))\). Los marginales para \(X\) y \(Y\) son los que se desea.
Los marginales son univariantes y, por lo tanto, pueden ser más fáciles de medir y / o modelar. Una cópula permite partir de marginales pero también lograr correlaciones arbitrarias entre dimensiones.
Cópula gaussiana
Para ilustrar cómo se construyen las cópulas, considérese el caso de capturar la dependencia según correlaciones gaussianas multivariadas. A Gaussian Cópula es una propuesta por \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) donde \(\Phi_\Sigma\) representa la CDF de un MultivariateNormal, con covarianza \(\Sigma\) y media 0, y \(\Phi^{-1}\) es el CDF inversa para la normal estándar.
La aplicación de la CDF inversa de la normal deforma las dimensiones uniformes para que se distribuyan normalmente. La aplicación de la CDF de la normal multivariada luego aplasta la distribución para que sea marginalmente uniforme y con correlaciones gaussianas.
Por lo tanto, lo que tenemos es que la cópula gaussiana es una distribución en la unidad hipercubo \([0, 1]^n\) con marginales uniformes.
Definido como tal, el Gaussian Cópula puede implementarse con tfd.TransformedDistribution y apropiado Bijector . Es decir, estamos transformando un MultivariateNormal, a través del uso de la distribución normal de CDF inversa, implementado por el tfb.NormalCDF bijector.
A continuación, se implementa un Gauss cópula con una suposición simplificadora: que la covarianza es parametrizado por un factor de Cholesky (de ahí una covarianza para MultivariateNormalTriL ). (Se podría utilizar otros tf.linalg.LinearOperators para codificar diferentes supuestos sin matriz.).
class GaussianCopulaTriL(tfd.TransformedDistribution):
"""Takes a location, and lower triangular matrix for the Cholesky factor."""
def __init__(self, loc, scale_tril):
super(GaussianCopulaTriL, self).__init__(
distribution=tfd.MultivariateNormalTriL(
loc=loc,
scale_tril=scale_tril),
bijector=tfb.NormalCDF(),
validate_args=False,
name="GaussianCopulaTriLUniform")
# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
[x_grid[..., np.newaxis],
y_grid[..., np.newaxis]], axis=-1)
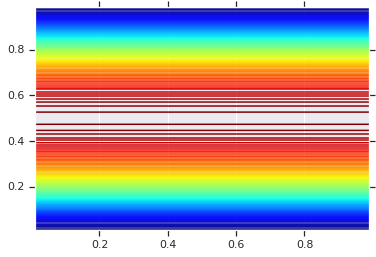
pdf = GaussianCopulaTriL(
loc=[0., 0.],
scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)
# Plot its density.
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
Sin embargo, el poder de tal modelo es usar la Transformada Integral de Probabilidad para usar la cópula en RV arbitrarios. De esta manera, podemos especificar marginales arbitrarias y usar la cópula para unirlas.
Empezamos con un modelo:
\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]
y el uso de la cópula de dos variables para obtener un RV \(Z\), que tiene marginales Kumaraswamy y Gumbel .
Comenzaremos trazando la distribución del producto generada por esos dos vehículos recreativos. Esto es solo para servir como un punto de comparación cuando aplicamos la cópula.
a = 2.0
b = 2.0
gloc = 0.
gscale = 1.
x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)
# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)
pdf = x.prob(x_grid) * y.prob(y_grid)
# Plot its density
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
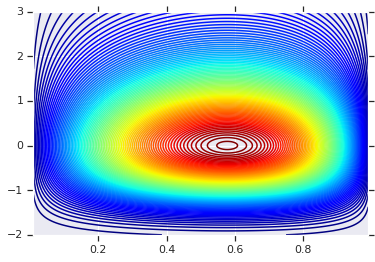
Distribución conjunta con diferentes marginales
Ahora usamos una cópula gaussiana para acoplar las distribuciones y graficar eso. Una vez más nuestra herramienta de elección se TransformedDistribution aplicando el apropiado Bijector para obtener los marginales elegidos.
Específicamente, se utiliza una Blockwise bijector que se aplica diferentes bijectors en diferentes partes del vector (que todavía es una transformación biyectiva).
Ahora podemos definir la Cópula que queremos. Dada una lista de los marginales objetivo (codificados como biyectores), podemos construir fácilmente una nueva distribución que use la cópula y tenga los marginales especificados.
class WarpedGaussianCopula(tfd.TransformedDistribution):
"""Application of a Gaussian Copula on a list of target marginals.
This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
which are distributed marginally (with CDF) [F_0, ... F_n],
`GaussianCopula` represents an application of the Copula, such that the
resulting multivariate distribution has the above specified marginals.
The marginals are specified by `marginal_bijectors`: These are
bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.
block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
length should be same as length of `marginal_bijectors`.
See tfb.Blockwise for details
"""
def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
super(WarpedGaussianCopula, self).__init__(
distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
bijector=tfb.Blockwise(bijectors=marginal_bijectors,
block_sizes=block_sizes),
validate_args=False,
name="GaussianCopula")
Finalmente, usemos esta cópula gaussiana. Usaremos un Cholesky de \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\), que corresponderá a las diferencias 1, y la correlación \(\rho\) para el normal multivariante.
Veremos algunos casos:
# Create our coordinates:
coordinates = np.concatenate(
[x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)
def create_gaussian_copula(correlation):
# Use Gaussian Copula to add dependence.
return WarpedGaussianCopula(
loc=[0., 0.],
scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
# These encode the marginals we want. In this case we want X_0 has
# Kumaraswamy marginal, and X_1 has Gumbel marginal.
marginal_bijectors=[
tfb.Invert(tfb.KumaraswamyCDF(a, b)),
tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])
# Note that the zero case will correspond to independent marginals!
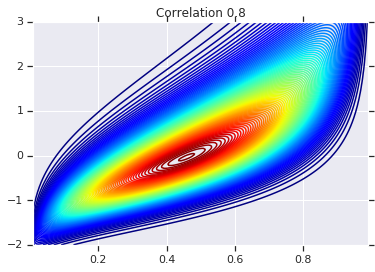
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
copula = create_gaussian_copula(correlation)
copulas.append(copula)
probs.append(copula.prob(coordinates))
# Plot it's density
for correlation, copula_prob in zip(correlations, probs):
plt.figure()
plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
plt.title('Correlation {}'.format(correlation))
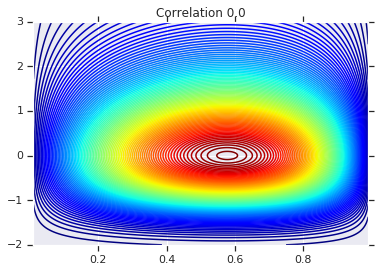
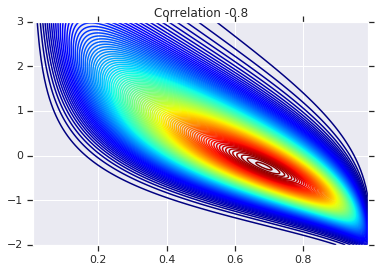
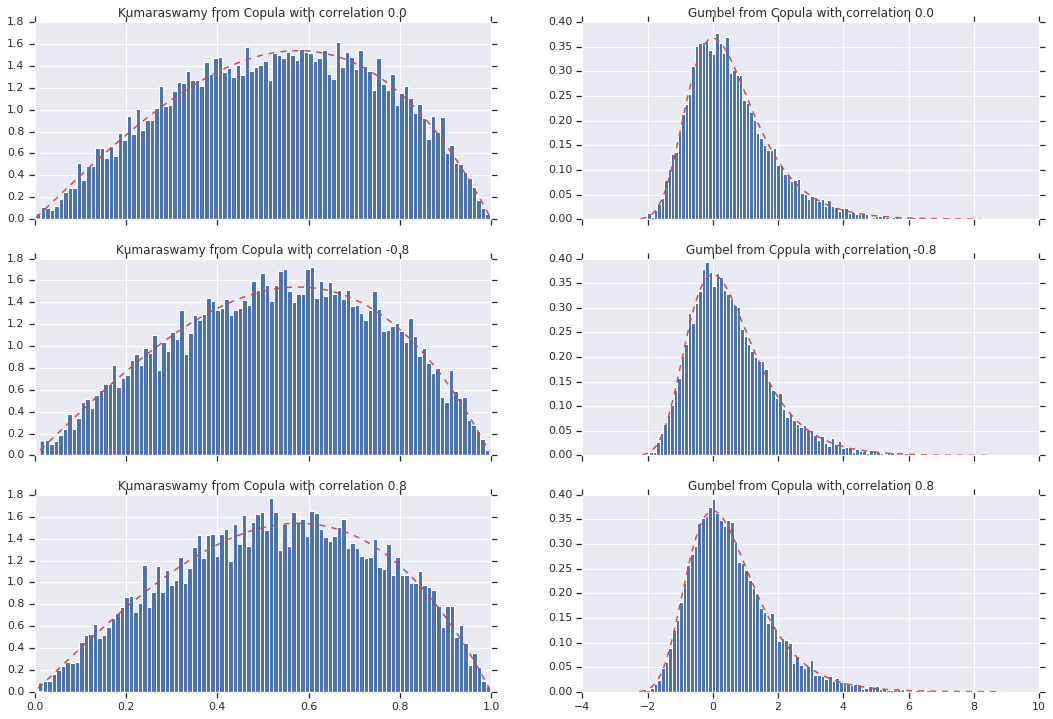
Finalmente, verifiquemos que realmente obtenemos los marginales que queremos.
def kumaraswamy_pdf(x):
return tfd.Kumaraswamy(a, b).prob(np.float32(x))
def gumbel_pdf(x):
return tfd.Gumbel(gloc, gscale).prob(np.float32(x))
copula_samples = []
for copula in copulas:
copula_samples.append(copula.sample(10000))
plot_rows = len(correlations)
plot_cols = 2 # for 2 densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))
# Let's marginalize out on each, and plot the samples.
for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
k = copula_sample[..., 0].numpy()
g = copula_sample[..., 1].numpy()
_, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))
_, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))
Conclusión
¡Y ahí vamos! Hemos demostrado que podemos construir Gauss cópulas con el Bijector API.
De manera más general, la escritura bijectors utilizando el Bijector activos y de los componen con una distribución, puede crear familias ricas de las distribuciones para el modelado flexible.
