Hỗn hợp giai thừa

Xem trên TensorFlow.org Chạy trong Google Colab Xem nguồn trên GitHub Tải xuống sổ ghi chép

Trong máy tính xách tay này, chúng ta thấy làm thế nào để sử dụng TensorFlow Xác suất (TFP) để lấy mẫu từ một hỗn hợp thừa của phân phối Gaussian định nghĩa là:\(p(x_1, ..., x_n) = \prod_i p_i(x_i)\) nơi: \(\begin{align*} p_i &\equiv \frac{1}{K}\sum_{k=1}^K \pi_{ik}\,\text{Normal}\left(\text{loc}=\mu_{ik},\, \text{scale}=\sigma_{ik}\right)\\1&=\sum_{k=1}^K\pi_{ik}, \forall i.\hphantom{MMMMMMMMMMM}\end{align*}\)

Mỗi biến \(x_i\) được mô phỏng như một hỗn hợp của Gaussian, và phân phối của doanh khắp \(n\) biến là sản phẩm của những mật độ.

Với một tập dữ liệu \(x^{(1)}, ..., x^{(T)}\), chúng tôi mô hình mỗi dataponit \(x^{(j)}\) như một hỗn hợp thừa của Gaussian:

\[p(x^{(j)}) = \prod_i p_i (x_i^{(j)})\]

Hỗn hợp giai thừa là một cách đơn giản để tạo phân phối với một số lượng nhỏ các tham số và một số lượng lớn các chế độ.

import tensorflow as tf
import numpy as np
import tensorflow_probability as tfp
import matplotlib.pyplot as plt
import seaborn as sns
tfd = tfp.distributions

# Use try/except so we can easily re-execute the whole notebook.
try:
  tf.enable_eager_execution()
except:
  pass

Xây dựng hỗn hợp giai thừa của người Gaussian bằng TFP

num_vars = 2        # Number of variables (`n` in formula).
var_dim = 1         # Dimensionality of each variable `x[i]`.
num_components = 3  # Number of components for each mixture (`K` in formula).
sigma = 5e-2        # Fixed standard deviation of each component.

# Choose some random (component) modes.
component_mean = tfd.Uniform().sample([num_vars, num_components, var_dim])

factorial_mog = tfd.Independent(
   tfd.MixtureSameFamily(
       # Assume uniform weight on each component.
       mixture_distribution=tfd.Categorical(
           logits=tf.zeros([num_vars, num_components])),
       components_distribution=tfd.MultivariateNormalDiag(
           loc=component_mean, scale_diag=[sigma])),
   reinterpreted_batch_ndims=1)

Chú ý sử dụng của chúng ta về tfd.Independent . Này "meta-phân phối" áp dụng một reduce_sum trong log_prob tính trên bìa phải reinterpreted_batch_ndims kích thước hàng loạt. Trong trường hợp của chúng tôi, số tiền này ra các biến DIMENSION chỉ để lại kích thước hàng loạt khi chúng tôi tính log_prob . Lưu ý rằng điều này không ảnh hưởng đến việc lấy mẫu.

Vẽ đồ thị mật độ

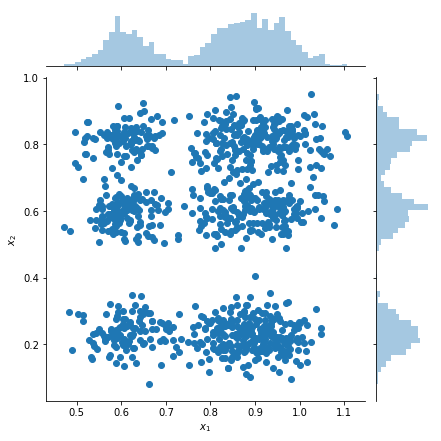
Tính toán mật độ trên một lưới các điểm và hiển thị vị trí của các chế độ bằng các ngôi sao màu đỏ. Mỗi chế độ trong hỗn hợp giai thừa tương ứng với một cặp phương thức từ hỗn hợp biến riêng cơ bản của Gaussian. Chúng ta có thể thấy 9 chế độ trong cốt truyện dưới đây, nhưng chúng ta chỉ cần 6 tham số (3 để xác định vị trí của các phương thức trong \(x_1\), và 3 để xác định vị trí của các phương thức trong \(x_2\)). Ngược lại, một hỗn hợp của phân phối Gaussian trong không gian 2d \((x_1, x_2)\) sẽ yêu cầu 2 * 9 = 18 thông số để xác định 9 chế độ.

plt.figure(figsize=(6,5))

# Compute density.
nx = 250 # Number of bins per dimension.
x = np.linspace(-3 * sigma, 1 + 3 * sigma, nx).astype('float32')
vals = tf.reshape(tf.stack(np.meshgrid(x, x), axis=2), (-1, num_vars, var_dim))
probs = factorial_mog.prob(vals).numpy().reshape(nx, nx)

# Display as image.
from matplotlib.colors import ListedColormap
cmap = ListedColormap(sns.color_palette("Blues", 256))
p = plt.pcolor(x, x, probs, cmap=cmap)
ax = plt.axis('tight');

# Plot locations of means.
means_np = component_mean.numpy().squeeze()
for mu_x in means_np[0]:
  for mu_y in means_np[1]:
    plt.scatter(mu_x, mu_y, s=150, marker='*', c='r', edgecolor='none');
plt.axis(ax);

plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.title('Density of factorial mixture of Gaussians');

png

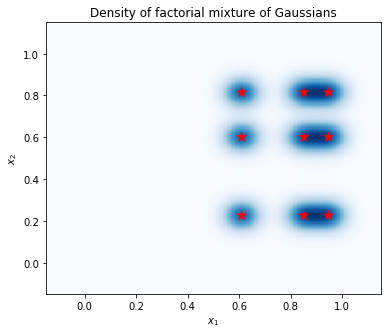
Mẫu đồ thị và ước tính mật độ cận biên

samples = factorial_mog.sample(1000).numpy()

g = sns.jointplot(
    x=samples[:, 0, 0],
    y=samples[:, 1, 0],
    kind="scatter",
    marginal_kws=dict(bins=50))
g.set_axis_labels("$x_1$", "$x_2$");

png