Mieszanka czynnikowa

Zobacz na TensorFlow.org

Uruchom w Google Colab

Wyświetl źródło na GitHub

Pobierz notatnik

W tym notesie pokażemy jak używać TensorFlow Prawdopodobieństwo (TFP) do próbki z silni Mieszanina dystrybucji Gaussians zdefiniowany jako:\(p(x_1, ..., x_n) = \prod_i p_i(x_i)\) gdzie: \(\begin{align*} p_i &\equiv \frac{1}{K}\sum_{k=1}^K \pi_{ik}\,\text{Normal}\left(\text{loc}=\mu_{ik},\, \text{scale}=\sigma_{ik}\right)\\1&=\sum_{k=1}^K\pi_{ik}, \forall i.\hphantom{MMMMMMMMMMM}\end{align*}\)

Każda zmienna \(x_i\) jest modelowany w postaci mieszaniny Gaussians i łącznego rozkładu na wszystkich \(n\) zmiennych jest produktem tych gęstościach.

Biorąc pod uwagę zestaw danych \(x^{(1)}, ..., x^{(T)}\), możemy modelować każdy dataponit \(x^{(j)}\) jako silni mieszaniny Gaussians:

\[p(x^{(j)}) = \prod_i p_i (x_i^{(j)})\]

Mieszaniny czynnikowe to prosty sposób tworzenia rozkładów o małej liczbie parametrów i dużej liczbie modów.

import tensorflow as tf
import numpy as np
import tensorflow_probability as tfp
import matplotlib.pyplot as plt
import seaborn as sns
tfd = tfp.distributions

# Use try/except so we can easily re-execute the whole notebook.
try:
  tf.enable_eager_execution()
except:
  pass

Zbuduj czynnikową mieszankę Gaussów za pomocą TFP

num_vars = 2        # Number of variables (`n` in formula).
var_dim = 1         # Dimensionality of each variable `x[i]`.
num_components = 3  # Number of components for each mixture (`K` in formula).
sigma = 5e-2        # Fixed standard deviation of each component.

# Choose some random (component) modes.
component_mean = tfd.Uniform().sample([num_vars, num_components, var_dim])

factorial_mog = tfd.Independent(
   tfd.MixtureSameFamily(
       # Assume uniform weight on each component.
       mixture_distribution=tfd.Categorical(
           logits=tf.zeros([num_vars, num_components])),
       components_distribution=tfd.MultivariateNormalDiag(
           loc=component_mean, scale_diag=[sigma])),
   reinterpreted_batch_ndims=1)

Zauważ nasze wykorzystanie tfd.Independent . Ten „meta-dystrybucją” stosuje reduce_sum w log_prob obliczania nad skrajnie prawych reinterpreted_batch_ndims wymiarach wsadowych. W naszym przypadku, to sumy spośród zmiennych wymiar pozostawiając jedynie wymiar wsadowy gdy obliczamy log_prob . Pamiętaj, że nie ma to wpływu na próbkowanie.

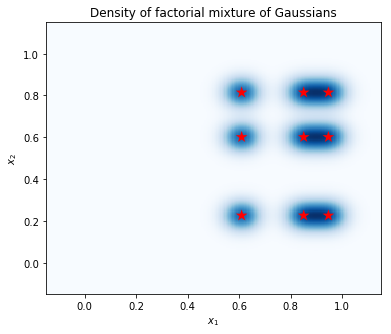
Wykreśl gęstość

Oblicz gęstość na siatce punktów i pokaż położenie modów z czerwonymi gwiazdami. Każdy mod w mieszaninie czynnikowej odpowiada parze modów z leżącej pod spodem mieszaniny gaussowskich zmiennych indywidualnych. Widzimy 9 trybów w poniższym wykresie, ale tylko potrzebne parametry 6 (3, aby określić rozmieszczenie sił w \(x_1\)i 3, aby określić rozmieszczenie sił w \(x_2\)). W przeciwieństwie do tego, mieszanina dystrybucji Gaussians w 2d przestrzeni \((x_1, x_2)\) wymagałoby 2 * 9 = 18, aby określić parametry trybów 9.

plt.figure(figsize=(6,5))

# Compute density.
nx = 250 # Number of bins per dimension.
x = np.linspace(-3 * sigma, 1 + 3 * sigma, nx).astype('float32')
vals = tf.reshape(tf.stack(np.meshgrid(x, x), axis=2), (-1, num_vars, var_dim))
probs = factorial_mog.prob(vals).numpy().reshape(nx, nx)

# Display as image.
from matplotlib.colors import ListedColormap
cmap = ListedColormap(sns.color_palette("Blues", 256))
p = plt.pcolor(x, x, probs, cmap=cmap)
ax = plt.axis('tight');

# Plot locations of means.
means_np = component_mean.numpy().squeeze()
for mu_x in means_np[0]:
  for mu_y in means_np[1]:
    plt.scatter(mu_x, mu_y, s=150, marker='*', c='r', edgecolor='none');
plt.axis(ax);

plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.title('Density of factorial mixture of Gaussians');

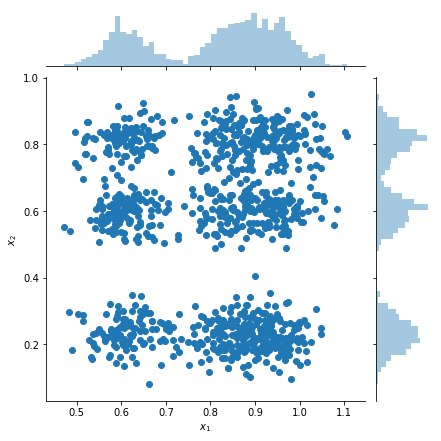
Próbki działkowe i oszacowania gęstości brzegowej

samples = factorial_mog.sample(1000).numpy()

g = sns.jointplot(
    x=samples[:, 0, 0],
    y=samples[:, 1, 0],
    kind="scatter",
    marginal_kws=dict(bins=50))
g.set_axis_labels("$x_1$", "$x_2$");