Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza la fonte su GitHub Visualizza la fonte su GitHub |  Scarica taccuino Scarica taccuino |
In questo notebook si mostra come utilizzare tensorflow Probabilità (TFP) per esempio da una miscela fattoriale di distribuzione gaussiane definito come:\(p(x_1, ..., x_n) = \prod_i p_i(x_i)\) dove: \(\begin{align*} p_i &\equiv \frac{1}{K}\sum_{k=1}^K \pi_{ik}\,\text{Normal}\left(\text{loc}=\mu_{ik},\, \text{scale}=\sigma_{ik}\right)\\1&=\sum_{k=1}^K\pi_{ik}, \forall i.\hphantom{MMMMMMMMMMM}\end{align*}\)
Ogni variabile \(x_i\) è modellato come una miscela di gaussiane, e la distribuzione congiunta su tutti \(n\) variabili è un prodotto di queste densità.
Dato un insieme di dati \(x^{(1)}, ..., x^{(T)}\), modelliamo ogni dataponit \(x^{(j)}\) come miscela fattoriale di gaussiane:
\[p(x^{(j)}) = \prod_i p_i (x_i^{(j)})\]
Le miscele fattoriali sono un modo semplice per creare distribuzioni con un numero limitato di parametri e un numero elevato di modalità.
import tensorflow as tf
import numpy as np
import tensorflow_probability as tfp
import matplotlib.pyplot as plt
import seaborn as sns
tfd = tfp.distributions
# Use try/except so we can easily re-execute the whole notebook.
try:
tf.enable_eager_execution()
except:
pass
Costruisci la miscela fattoriale di gaussiane usando TFP
num_vars = 2 # Number of variables (`n` in formula).
var_dim = 1 # Dimensionality of each variable `x[i]`.
num_components = 3 # Number of components for each mixture (`K` in formula).
sigma = 5e-2 # Fixed standard deviation of each component.
# Choose some random (component) modes.
component_mean = tfd.Uniform().sample([num_vars, num_components, var_dim])
factorial_mog = tfd.Independent(
tfd.MixtureSameFamily(
# Assume uniform weight on each component.
mixture_distribution=tfd.Categorical(
logits=tf.zeros([num_vars, num_components])),
components_distribution=tfd.MultivariateNormalDiag(
loc=component_mean, scale_diag=[sigma])),
reinterpreted_batch_ndims=1)
Si noti il nostro uso di tfd.Independent . Questo "meta-distribuzione" applica una reduce_sum nel log_prob calcolo sui più a destra reinterpreted_batch_ndims dimensioni batch. Nel nostro caso, questo somme le variabili di quota lasciando solo la dimensione batch quando calcoliamo log_prob . Si noti che ciò non influisce sul campionamento.
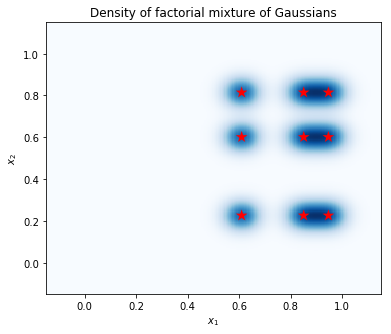
Traccia la densità
Calcola la densità su una griglia di punti e mostra le posizioni dei modi con le stelle rosse. Ciascun modo nella miscela fattoriale corrisponde a una coppia di modi della miscela gaussiana di variabili individuali sottostante. Possiamo vedere 9 modalità nella trama di sotto, ma abbiamo solo bisogno di 6 parametri (3 per specificare le posizioni dei modi in \(x_1\), e 3 per specificare le posizioni dei modi in \(x_2\)). Al contrario, una miscela di distribuzione gaussiane nello spazio 2d \((x_1, x_2)\) richiederebbe 2 * 9 = 18 parametri per specificare le modalità 9.
plt.figure(figsize=(6,5))
# Compute density.
nx = 250 # Number of bins per dimension.
x = np.linspace(-3 * sigma, 1 + 3 * sigma, nx).astype('float32')
vals = tf.reshape(tf.stack(np.meshgrid(x, x), axis=2), (-1, num_vars, var_dim))
probs = factorial_mog.prob(vals).numpy().reshape(nx, nx)
# Display as image.
from matplotlib.colors import ListedColormap
cmap = ListedColormap(sns.color_palette("Blues", 256))
p = plt.pcolor(x, x, probs, cmap=cmap)
ax = plt.axis('tight');
# Plot locations of means.
means_np = component_mean.numpy().squeeze()
for mu_x in means_np[0]:
for mu_y in means_np[1]:
plt.scatter(mu_x, mu_y, s=150, marker='*', c='r', edgecolor='none');
plt.axis(ax);
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.title('Density of factorial mixture of Gaussians');
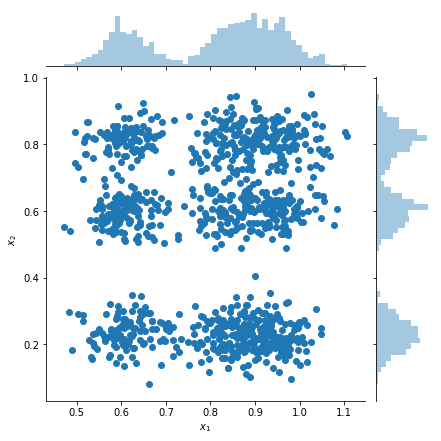
Campioni di grafici e stime della densità marginale
samples = factorial_mog.sample(1000).numpy()
g = sns.jointplot(
x=samples[:, 0, 0],
y=samples[:, 1, 0],
kind="scatter",
marginal_kws=dict(bins=50))
g.set_axis_labels("$x_1$", "$x_2$");