Campuran Faktorial

Lihat di TensorFlow.org

Jalankan di Google Colab

Lihat sumber di GitHub

Unduh buku catatan

Dalam notebook ini kita menunjukkan bagaimana menggunakan TensorFlow Probabilitas (TFP) untuk sampel dari Campuran faktorial distribusi Gaussians didefinisikan sebagai:\(p(x_1, ..., x_n) = \prod_i p_i(x_i)\) mana: \(\begin{align*} p_i &\equiv \frac{1}{K}\sum_{k=1}^K \pi_{ik}\,\text{Normal}\left(\text{loc}=\mu_{ik},\, \text{scale}=\sigma_{ik}\right)\\1&=\sum_{k=1}^K\pi_{ik}, \forall i.\hphantom{MMMMMMMMMMM}\end{align*}\)

Masing-masing variabel \(x_i\) dimodelkan sebagai campuran Gaussians, dan distribusi gabungan atas semua \(n\) variabel merupakan produk kepadatan tersebut.

Mengingat dataset \(x^{(1)}, ..., x^{(T)}\), kita model masing-masing dataponit \(x^{(j)}\) sebagai campuran faktorial Gaussians:

\[p(x^{(j)}) = \prod_i p_i (x_i^{(j)})\]

Campuran faktorial adalah cara sederhana untuk membuat distribusi dengan sejumlah kecil parameter dan sejumlah besar mode.

import tensorflow as tf
import numpy as np
import tensorflow_probability as tfp
import matplotlib.pyplot as plt
import seaborn as sns
tfd = tfp.distributions

# Use try/except so we can easily re-execute the whole notebook.
try:
  tf.enable_eager_execution()
except:
  pass

Bangun Campuran Faktorial Gauss menggunakan TFP

num_vars = 2        # Number of variables (`n` in formula).
var_dim = 1         # Dimensionality of each variable `x[i]`.
num_components = 3  # Number of components for each mixture (`K` in formula).
sigma = 5e-2        # Fixed standard deviation of each component.

# Choose some random (component) modes.
component_mean = tfd.Uniform().sample([num_vars, num_components, var_dim])

factorial_mog = tfd.Independent(
   tfd.MixtureSameFamily(
       # Assume uniform weight on each component.
       mixture_distribution=tfd.Categorical(
           logits=tf.zeros([num_vars, num_components])),
       components_distribution=tfd.MultivariateNormalDiag(
           loc=component_mean, scale_diag=[sigma])),
   reinterpreted_batch_ndims=1)

Perhatikan penggunaan kami tfd.Independent . Ini "meta-distribusi" menerapkan reduce_sum di log_prob perhitungan di atas paling kanan reinterpreted_batch_ndims dimensi batch. Dalam kasus kami, jumlah ini keluar variabel dimensi hanya menyisakan dimensi bets ketika kita menghitung log_prob . Perhatikan bahwa ini tidak memengaruhi pengambilan sampel.

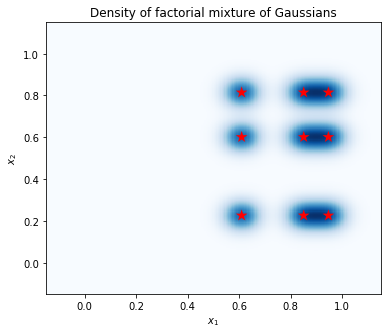
Gambarkan Kepadatannya

Hitung kerapatan pada kisi titik, dan tunjukkan lokasi mode dengan bintang merah. Setiap mode dalam campuran faktorial sesuai dengan sepasang mode dari campuran individu-variabel Gauss yang mendasarinya. Kita bisa melihat 9 mode di plot di bawah ini, tapi kami hanya membutuhkan 6 parameter (3 untuk menentukan lokasi dari mode di \(x_1\), dan 3 untuk menentukan lokasi dari mode di \(x_2\)). Sebaliknya, campuran distribusi Gaussians di 2d ruang \((x_1, x_2)\) akan membutuhkan 2 * 9 = 18 parameter untuk menentukan 9 mode.

plt.figure(figsize=(6,5))

# Compute density.
nx = 250 # Number of bins per dimension.
x = np.linspace(-3 * sigma, 1 + 3 * sigma, nx).astype('float32')
vals = tf.reshape(tf.stack(np.meshgrid(x, x), axis=2), (-1, num_vars, var_dim))
probs = factorial_mog.prob(vals).numpy().reshape(nx, nx)

# Display as image.
from matplotlib.colors import ListedColormap
cmap = ListedColormap(sns.color_palette("Blues", 256))
p = plt.pcolor(x, x, probs, cmap=cmap)
ax = plt.axis('tight');

# Plot locations of means.
means_np = component_mean.numpy().squeeze()
for mu_x in means_np[0]:
  for mu_y in means_np[1]:
    plt.scatter(mu_x, mu_y, s=150, marker='*', c='r', edgecolor='none');
plt.axis(ax);

plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.title('Density of factorial mixture of Gaussians');

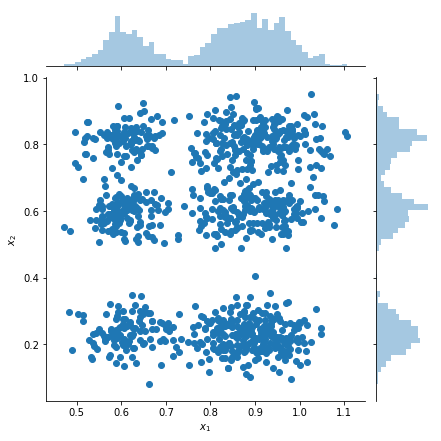
Plot sampel dan perkiraan kepadatan marjinal

samples = factorial_mog.sample(1000).numpy()

g = sns.jointplot(
    x=samples[:, 0, 0],
    y=samples[:, 1, 0],
    kind="scatter",
    marginal_kws=dict(bins=50))
g.set_axis_labels("$x_1$", "$x_2$");