مخلوط فاکتوریل

مشاهده در TensorFlow.org

در Google Colab اجرا شود

مشاهده منبع در GitHub

دانلود دفترچه یادداشت

در این نوت بوک ما نشان می دهد که چگونه به استفاده TensorFlow احتمال (TFP) به نمونه از یک مخلوط فاکتوریل توزیع Gaussians تعریف می شود:\(p(x_1, ..., x_n) = \prod_i p_i(x_i)\) که در آن: \(\begin{align*} p_i &\equiv \frac{1}{K}\sum_{k=1}^K \pi_{ik}\,\text{Normal}\left(\text{loc}=\mu_{ik},\, \text{scale}=\sigma_{ik}\right)\\1&=\sum_{k=1}^K\pi_{ik}, \forall i.\hphantom{MMMMMMMMMMM}\end{align*}\)

هر متغیر \(x_i\) به عنوان یک مخلوطی از Gaussians و توزیع مشترک بیش از همه مدل \(n\) متغیرهای یک محصول از این میزان تراکم است.

با توجه به یک مجموعه داده \(x^{(1)}, ..., x^{(T)}\)، ما مدل هر dataponit \(x^{(j)}\) به عنوان یک مخلوط فاکتوریل Gaussians:

\[p(x^{(j)}) = \prod_i p_i (x_i^{(j)})\]

مخلوط های فاکتوریال یک راه ساده برای ایجاد توزیع با تعداد کمی پارامتر و تعداد زیادی حالت هستند.

import tensorflow as tf
import numpy as np
import tensorflow_probability as tfp
import matplotlib.pyplot as plt
import seaborn as sns
tfd = tfp.distributions

# Use try/except so we can easily re-execute the whole notebook.
try:
  tf.enable_eager_execution()
except:
  pass

مخلوط فاکتوریال گاوسیان را با استفاده از TFP بسازید

num_vars = 2        # Number of variables (`n` in formula).
var_dim = 1         # Dimensionality of each variable `x[i]`.
num_components = 3  # Number of components for each mixture (`K` in formula).
sigma = 5e-2        # Fixed standard deviation of each component.

# Choose some random (component) modes.
component_mean = tfd.Uniform().sample([num_vars, num_components, var_dim])

factorial_mog = tfd.Independent(
   tfd.MixtureSameFamily(
       # Assume uniform weight on each component.
       mixture_distribution=tfd.Categorical(
           logits=tf.zeros([num_vars, num_components])),
       components_distribution=tfd.MultivariateNormalDiag(
           loc=component_mean, scale_diag=[sigma])),
   reinterpreted_batch_ndims=1)

توجه داشته باشید استفاده ما از tfd.Independent . این "متا توزیع" یک امر reduce_sum در log_prob محاسبه بیش از سمت راست reinterpreted_batch_ndims ابعاد دسته ای. در مورد ما، این مبالغ از متغیرهای ابعاد روم تنها بعد دسته ای هنگامی که ما محاسبه log_prob . توجه داشته باشید که این روی نمونه گیری تاثیری ندارد.

چگالی را ترسیم کنید

چگالی را روی شبکه ای از نقاط محاسبه کنید و مکان حالت ها را با ستاره های قرمز نشان دهید. هر حالت در مخلوط فاکتوریل مربوط به یک جفت حالت از مخلوط فردی-متغیر زیرین گاوسیان است. ما می توانیم 9 حالت در طرح زیر را ببینید، اما ما تنها نیاز 6 پارامتر (3 برای مشخص کردن مکان از حالت در \(x_1\)و 3 برای مشخص کردن مکان از حالت در \(x_2\)). در مقابل، مخلوطی از توزیع Gaussians در فضای 2D \((x_1, x_2)\) نیاز 2 * 9 = 18 پارامتر برای مشخص کردن 9 حالت.

plt.figure(figsize=(6,5))

# Compute density.
nx = 250 # Number of bins per dimension.
x = np.linspace(-3 * sigma, 1 + 3 * sigma, nx).astype('float32')
vals = tf.reshape(tf.stack(np.meshgrid(x, x), axis=2), (-1, num_vars, var_dim))
probs = factorial_mog.prob(vals).numpy().reshape(nx, nx)

# Display as image.
from matplotlib.colors import ListedColormap
cmap = ListedColormap(sns.color_palette("Blues", 256))
p = plt.pcolor(x, x, probs, cmap=cmap)
ax = plt.axis('tight');

# Plot locations of means.
means_np = component_mean.numpy().squeeze()
for mu_x in means_np[0]:
  for mu_y in means_np[1]:
    plt.scatter(mu_x, mu_y, s=150, marker='*', c='r', edgecolor='none');
plt.axis(ax);

plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.title('Density of factorial mixture of Gaussians');

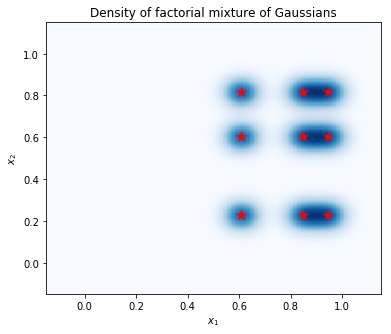
نمونه های پلات و برآورد تراکم حاشیه ای

samples = factorial_mog.sample(1000).numpy()

g = sns.jointplot(
    x=samples[:, 0, 0],
    y=samples[:, 1, 0],
    kind="scatter",
    marginal_kws=dict(bins=50))
g.set_axis_labels("$x_1$", "$x_2$");