ফ্যাক্টরিয়াল মিশ্রণ

TensorFlow.org এ দেখুন

Google Colab-এ চালান

GitHub-এ উৎস দেখুন

নোটবুক ডাউনলোড করুন

এই নোটবুক আমরা কিভাবে ব্যবহার করতে দেন TensorFlow সম্ভাব্যতা : হিসাবে সংজ্ঞায়িত করা Gaussians বিতরণের একটি গৌণিক মিশ্রণ থেকে নমুনা (TFP)\(p(x_1, ..., x_n) = \prod_i p_i(x_i)\) যেখানে: \(\begin{align*} p_i &\equiv \frac{1}{K}\sum_{k=1}^K \pi_{ik}\,\text{Normal}\left(\text{loc}=\mu_{ik},\, \text{scale}=\sigma_{ik}\right)\\1&=\sum_{k=1}^K\pi_{ik}, \forall i.\hphantom{MMMMMMMMMMM}\end{align*}\)

প্রতিটি পরিবর্তনশীল \(x_i\) Gaussians মিশ্রণ, এবং সর্বাঙ্গে যৌথ ডিস্ট্রিবিউশন হিসেবে স্থাপিত হয় \(n\) ভেরিয়েবল এই ঘনত্বের একটি পণ্য।

একটি ডেটাসেটের প্রদত্ত \(x^{(1)}, ..., x^{(T)}\), আমরা প্রতিটি dataponit মডেল \(x^{(j)}\) Gaussians একটি গৌণিক মিশ্রণ হিসাবে:

\[p(x^{(j)}) = \prod_i p_i (x_i^{(j)})\]

ফ্যাক্টরিয়াল মিশ্রণ হল অল্প সংখ্যক পরামিতি এবং প্রচুর সংখ্যক মোড সহ বিতরণ তৈরি করার একটি সহজ উপায়।

import tensorflow as tf
import numpy as np
import tensorflow_probability as tfp
import matplotlib.pyplot as plt
import seaborn as sns
tfd = tfp.distributions

# Use try/except so we can easily re-execute the whole notebook.
try:
  tf.enable_eager_execution()
except:
  pass

TFP ব্যবহার করে গাউসিয়ানদের ফ্যাক্টরিয়াল মিশ্রণ তৈরি করুন

num_vars = 2        # Number of variables (`n` in formula).
var_dim = 1         # Dimensionality of each variable `x[i]`.
num_components = 3  # Number of components for each mixture (`K` in formula).
sigma = 5e-2        # Fixed standard deviation of each component.

# Choose some random (component) modes.
component_mean = tfd.Uniform().sample([num_vars, num_components, var_dim])

factorial_mog = tfd.Independent(
   tfd.MixtureSameFamily(
       # Assume uniform weight on each component.
       mixture_distribution=tfd.Categorical(
           logits=tf.zeros([num_vars, num_components])),
       components_distribution=tfd.MultivariateNormalDiag(
           loc=component_mean, scale_diag=[sigma])),
   reinterpreted_batch_ndims=1)

আমাদের ব্যবহার লক্ষ্য করুন tfd.Independent । এই "মেটা-বন্টন" একটি প্রযোজ্য reduce_sum মধ্যে log_prob ডানদিকের উপর হিসাব reinterpreted_batch_ndims ব্যাচ মাত্রা। আমাদের ক্ষেত্রে, আউট ভেরিয়েবল এই অঙ্কের শুধুমাত্র ব্যাচ মাত্রা রেখে মাত্রা যখন আমরা গনা log_prob । মনে রাখবেন যে এটি নমুনাকে প্রভাবিত করে না।

ঘনত্ব প্লট

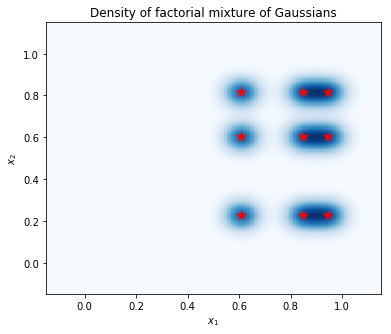
পয়েন্টগুলির একটি গ্রিডে ঘনত্ব গণনা করুন এবং লাল তারা দিয়ে মোডগুলির অবস্থানগুলি দেখান৷ ফ্যাক্টোরিয়াল মিশ্রণের প্রতিটি মোড গাউসিয়ানদের অন্তর্নিহিত স্বতন্ত্র-পরিবর্তনশীল মিশ্রণ থেকে এক জোড়া মোডের সাথে মিলে যায়। আমরা নিচের চক্রান্ত 9 মোড দেখতে পারেন, কিন্তু আমরা মাত্র 6 পরামিতি প্রয়োজন (3 মোড অবস্থানে নির্দিষ্ট করার \(x_1\), এবং 3 মোড অবস্থানে নির্দিষ্ট করার \(x_2\))। এর বিপরীতে, 2d স্থান Gaussians বন্টন মিশ্রণ \((x_1, x_2)\) 9 মোড উল্লেখ করার 2 * 9 = 18 পরামিতি প্রয়োজন।

plt.figure(figsize=(6,5))

# Compute density.
nx = 250 # Number of bins per dimension.
x = np.linspace(-3 * sigma, 1 + 3 * sigma, nx).astype('float32')
vals = tf.reshape(tf.stack(np.meshgrid(x, x), axis=2), (-1, num_vars, var_dim))
probs = factorial_mog.prob(vals).numpy().reshape(nx, nx)

# Display as image.
from matplotlib.colors import ListedColormap
cmap = ListedColormap(sns.color_palette("Blues", 256))
p = plt.pcolor(x, x, probs, cmap=cmap)
ax = plt.axis('tight');

# Plot locations of means.
means_np = component_mean.numpy().squeeze()
for mu_x in means_np[0]:
  for mu_y in means_np[1]:
    plt.scatter(mu_x, mu_y, s=150, marker='*', c='r', edgecolor='none');
plt.axis(ax);

plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.title('Density of factorial mixture of Gaussians');

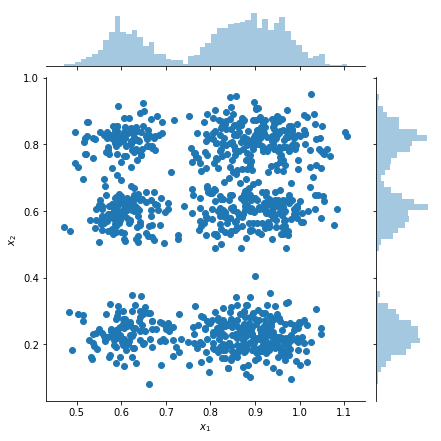
প্লট নমুনা এবং প্রান্তিক ঘনত্ব অনুমান

samples = factorial_mog.sample(1000).numpy()

g = sns.jointplot(
    x=samples[:, 0, 0],
    y=samples[:, 1, 0],
    kind="scatter",
    marginal_kws=dict(bins=50))
g.set_axis_labels("$x_1$", "$x_2$");