FFJORD

Visualizza su TensorFlow.org Esegui in Google Colab Visualizza la fonte su GitHub Scarica taccuino

Impostare

Prima installa i pacchetti utilizzati in questa demo.

pip install -q dm-sonnet

Importazioni (tf, tfp con trucco aggiunto, ecc.)

import numpy as np
import tqdm as tqdm
import sklearn.datasets as skd

# visualization
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import kde

# tf and friends
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
import sonnet as snt
tf.enable_v2_behavior()

tfb = tfp.bijectors
tfd = tfp.distributions

def make_grid(xmin, xmax, ymin, ymax, gridlines, pts):
  xpts = np.linspace(xmin, xmax, pts)
  ypts = np.linspace(ymin, ymax, pts)
  xgrid = np.linspace(xmin, xmax, gridlines)
  ygrid = np.linspace(ymin, ymax, gridlines)
  xlines = np.stack([a.ravel() for a in np.meshgrid(xpts, ygrid)])
  ylines = np.stack([a.ravel() for a in np.meshgrid(xgrid, ypts)])
  return np.concatenate([xlines, ylines], 1).T

grid = make_grid(-3, 3, -3, 3, 4, 100)

/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.
  import pandas.util.testing as tm

Funzioni di supporto per la visualizzazione

Biettore FFJORD

In questa collaborazione dimostriamo FFJORD bijector, originariamente proposto nell'articolo di Grathwohl, Will, et al. arXiv di collegamento .

In sintesi l'idea dietro questo approccio è quello di stabilire una corrispondenza tra una distribuzione di base nota e la distribuzione dei dati.

Per stabilire questa connessione, dobbiamo

  1. Definire una mappa biunivoca \(\mathcal{T}_{\theta}:\mathbf{x} \rightarrow \mathbf{y}\), \(\mathcal{T}_{\theta}^{1}:\mathbf{y} \rightarrow \mathbf{x}\) tra lo spazio \(\mathcal{Y}\) su cui è definita la distribuzione di base e lo spazio \(\mathcal{X}\) del dominio di dati.
  2. In modo efficiente tenere traccia delle deformazioni che compiamo per trasferire la nozione di probabilità su \(\mathcal{X}\).

La seconda condizione è formalizzata nella seguente espressione per la distribuzione di probabilità definita su \(\mathcal{X}\):

\[ \log p_{\mathbf{x} }(\mathbf{x})=\log p_{\mathbf{y} }(\mathbf{y})-\log \operatorname{det}\left|\frac{\partial \mathcal{T}_{\theta}(\mathbf{y})}{\partial \mathbf{y} }\right| \]

FFJORD bijector realizza questo definendo una trasformazione

\[ \mathcal{T_{\theta} }: \mathbf{x} = \mathbf{z}(t_{0}) \rightarrow \mathbf{y} = \mathbf{z}(t_{1}) \quad : \quad \frac{d \mathbf{z} }{dt} = \mathbf{f}(t, \mathbf{z}, \theta) \]

Questa trasformazione è invertibile, purché funzione \(\mathbf{f}\) che descrive l'evoluzione dello stato \(\mathbf{z}\) è ben comportata e il log_det_jacobian può essere calcolata integrando la seguente espressione.

\[ \log \operatorname{det}\left|\frac{\partial \mathcal{T}_{\theta}(\mathbf{y})}{\partial \mathbf{y} }\right| = -\int_{t_{0} }^{t_{1} } \operatorname{Tr}\left(\frac{\partial \mathbf{f}(t, \mathbf{z}, \theta)}{\partial \mathbf{z}(t)}\right) d t \]

In questa demo formeremo un bijector FFJORD per deformare una distribuzione gaussiana sulla distribuzione definita da moons set di dati. Questo sarà fatto in 3 passaggi:

  • Definire distribuzione di base
  • Definisci il biettore FFJORD
  • Riduci al minimo l'esatta probabilità di log del set di dati

Per prima cosa, carichiamo i dati

set di dati

png

Successivamente, istanziamo una distribuzione di base

base_loc = np.array([0.0, 0.0]).astype(np.float32)
base_sigma = np.array([0.8, 0.8]).astype(np.float32)
base_distribution = tfd.MultivariateNormalDiag(base_loc, base_sigma)

Usiamo un multi-layer Perceptron a modello state_derivative_fn .

Anche se non è necessario per questo insieme di dati, è spesso benefitial fare state_derivative_fn dipendente dal tempo. Qui raggiungiamo questo concatenando t agli ingressi della nostra rete.

class MLP_ODE(snt.Module):
  """Multi-layer NN ode_fn."""
  def __init__(self, num_hidden, num_layers, num_output, name='mlp_ode'):
    super(MLP_ODE, self).__init__(name=name)
    self._num_hidden = num_hidden
    self._num_output = num_output
    self._num_layers = num_layers
    self._modules = []
    for _ in range(self._num_layers - 1):
      self._modules.append(snt.Linear(self._num_hidden))
      self._modules.append(tf.math.tanh)
    self._modules.append(snt.Linear(self._num_output))
    self._model = snt.Sequential(self._modules)

  def __call__(self, t, inputs):
    inputs = tf.concat([tf.broadcast_to(t, inputs.shape), inputs], -1)
    return self._model(inputs)

Modello e parametri di allenamento

Ora costruiamo una pila di biiettori FFJORD. Ogni bijector è provvista ode_solve_fn e trace_augmentation_fn ed è proprio state_derivative_fn modello, in modo che essi rappresentano una sequenza di trasformazioni diverse.

Biettore da costruzione

Ora possiamo usare TransformedDistribution che è il risultato di orditura base_distribution con stacked_ffjord bijector.

transformed_distribution = tfd.TransformedDistribution(
    distribution=base_distribution, bijector=stacked_ffjord)

Ora definiamo la nostra procedura di addestramento. Riduciamo semplicemente al minimo la probabilità di log negativa dei dati.

Formazione

Campioni

Tracciare campioni da distribuzioni base e trasformate.

evaluation_samples = []
base_samples, transformed_samples = get_samples()
transformed_grid = get_transformed_grid()
evaluation_samples.append((base_samples, transformed_samples, transformed_grid))

WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/ops/resource_variable_ops.py:1817: calling BaseResourceVariable.__init__ (from tensorflow.python.ops.resource_variable_ops) with constraint is deprecated and will be removed in a future version.
Instructions for updating:
If using Keras pass *_constraint arguments to layers.

panel_id = 0
panel_data = evaluation_samples[panel_id]
fig, axarray = plt.subplots(
  1, 4, figsize=(16, 6))
plot_panel(
    grid, panel_data[0], panel_data[2], panel_data[1], moons, axarray, False)
plt.tight_layout()

png

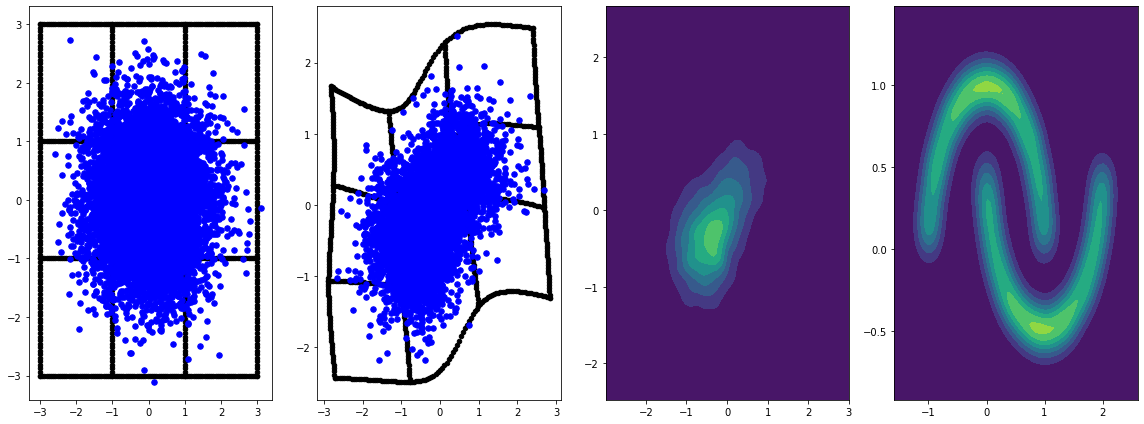
learning_rate = tf.Variable(LR, trainable=False)
optimizer = snt.optimizers.Adam(learning_rate)

for epoch in tqdm.trange(NUM_EPOCHS // 2):
  base_samples, transformed_samples = get_samples()
  transformed_grid = get_transformed_grid()
  evaluation_samples.append(
      (base_samples, transformed_samples, transformed_grid))
  for batch in moons_ds:
    _ = train_step(optimizer, batch)

0%|          | 0/40 [00:00<?, ?it/s]
WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow_probability/python/math/ode/base.py:350: calling while_loop_v2 (from tensorflow.python.ops.control_flow_ops) with back_prop=False is deprecated and will be removed in a future version.
Instructions for updating:
back_prop=False is deprecated. Consider using tf.stop_gradient instead.
Instead of:
results = tf.while_loop(c, b, vars, back_prop=False)
Use:
results = tf.nest.map_structure(tf.stop_gradient, tf.while_loop(c, b, vars))
100%|██████████| 40/40 [07:00<00:00, 10.52s/it]

panel_id = -1
panel_data = evaluation_samples[panel_id]
fig, axarray = plt.subplots(
  1, 4, figsize=(16, 6))
plot_panel(grid, panel_data[0], panel_data[2], panel_data[1], moons, axarray)
plt.tight_layout()

png

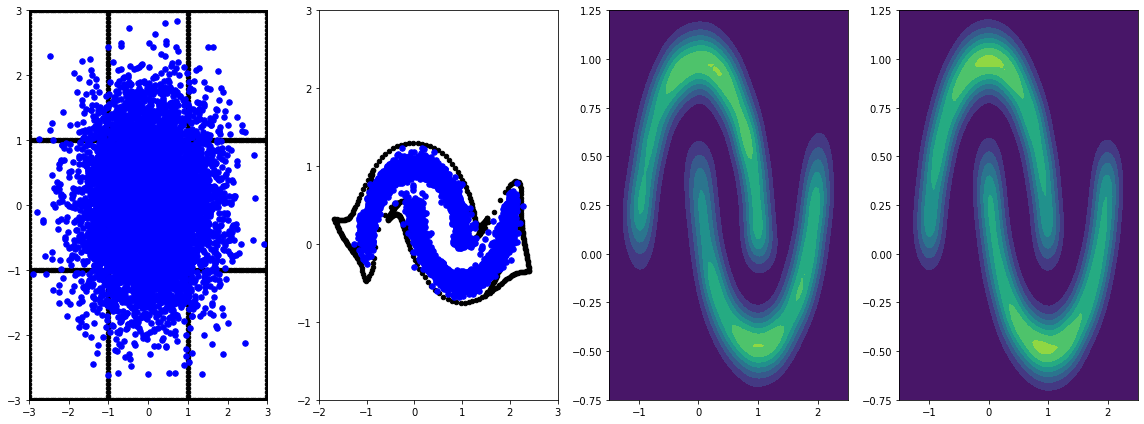
Allenarlo più a lungo con il tasso di apprendimento si traduce in ulteriori miglioramenti.

Non convertito in questo esempio, FFJORD bijector supporta la stima della traccia stocastica di hutchinson. La particolare stimatore può essere fornito tramite trace_augmentation_fn . Allo stesso modo gli integratori alternativi possono essere utilizzati definendo personalizzato ode_solve_fn .