मॉडलिंग COVID-19 यूरोप में फैल गया और हस्तक्षेपों का प्रभाव

एमआईटी लाइसेंस के तहत लाइसेंस प्राप्त

TensorFlow.org पर देखें Google Colab में चलाएं GitHub पर स्रोत देखें नोटबुक डाउनलोड करें

2020 की शुरुआत में COVID-19 के प्रसार को धीमा करने के लिए, यूरोपीय देशों ने गैर-फार्मास्युटिकल हस्तक्षेपों को अपनाया जैसे कि गैर-आवश्यक व्यवसायों को बंद करना, व्यक्तिगत मामलों को अलग करना, यात्रा प्रतिबंध, और सामाजिक दूरी को प्रोत्साहित करने के लिए अन्य उपाय। इंपीरियल कॉलेज COVID -19 रिस्पांस टीम उनके समाचार पत्र में इन उपायों की प्रभावशीलता का विश्लेषण किया "संक्रमण की संख्या और 11 यूरोपीय देशों में COVID -19 पर गैर दवा हस्तक्षेप के प्रभाव का आकलन" , एक यंत्रवत के साथ संयुक्त एक बायेसियन श्रेणीबद्ध मॉडल का उपयोग महामारी विज्ञान मॉडल।

इस Colab में उस विश्लेषण का एक TensorFlow Probability (TFP) कार्यान्वयन शामिल है, जिसे निम्नानुसार व्यवस्थित किया गया है:

  • "मॉडल सेटअप" रोग संचरण और परिणामी मौतों के लिए महामारी विज्ञान मॉडल को परिभाषित करता है, मॉडल मापदंडों पर बायेसियन पूर्व वितरण, और पैरामीटर मानों पर सशर्त मौतों की संख्या का वितरण।
  • "डेटा प्रीप्रोसेसिंग" प्रत्येक देश में समय और हस्तक्षेप के प्रकार, समय के साथ मौतों की संख्या और संक्रमित लोगों के लिए अनुमानित मृत्यु दर पर डेटा में लोड होता है।
  • "मॉडल अनुमान" एक बायेसियन पदानुक्रमित मॉडल बनाता है और हेमिल्टनियन मोंटे कार्लो (एचएमसी) को पैरामीटर पर पश्च वितरण से नमूना लेने के लिए चलाता है।
  • "परिणाम" ब्याज की मात्रा जैसे पूर्वानुमानित मौतों और हस्तक्षेपों के अभाव में प्रतितथ्यात्मक मौतों के लिए पश्च-पूर्वानुमान वितरण को दर्शाता है।

कागज सबूत है कि देशों प्रत्येक संक्रमित व्यक्ति (द्वारा प्रेषित नए संक्रमणों की संख्या को कम करने में कामयाब था पाया\(R_t\)), लेकिन यह विश्वसनीय अंतराल निहित \(R_t=1\) (मूल्य जो ऊपर महामारी फैल जारी है) और यह समय से पहले किया गया है कि हस्तक्षेपों की प्रभावशीलता पर मजबूत निष्कर्ष निकालने के लिए। कागज के लिए स्टेन कोड लेखकों में है Github भंडार है, और इस Colab reproduces संस्करण 2 ।

pip3 install -q git+git://github.com/arviz-devs/arviz.git
pip3 install -q tf-nightly tfp-nightly

आयात

1 मॉडल सेटअप

1.1 संक्रमण और मौतों के लिए यंत्रवत मॉडल

संक्रमण मॉडल समय के साथ प्रत्येक देश में संक्रमणों की संख्या का अनुकरण करता है। इनपुट डेटा समय और हस्तक्षेप का प्रकार, जनसंख्या का आकार और प्रारंभिक मामले हैं। पैरामीटर हस्तक्षेप की प्रभावशीलता और रोग संचरण की दर को नियंत्रित करते हैं। मौतों की अपेक्षित संख्या के लिए मॉडल अनुमानित संक्रमणों के लिए एक घातक दर लागू करता है।

संक्रमण मॉडल सीरियल अंतराल वितरण (संक्रमित होने और किसी और को संक्रमित करने के बीच दिनों की संख्या पर वितरण) के साथ पिछले दैनिक संक्रमणों का एक दृढ़ संकल्प करता है। हर बार कदम पर, समय में नए संक्रमणों की संख्या \(t\), \(n_t\), के रूप में गणना की जाती है

\शुरू {समीकरण} \sum_{i=0}^{t-1} n_i \mu_t \text{p} (\text{किसी संक्रमित व्यक्ति से पकड़ा गया} i | \text{नया संक्रमित } t) \end{ समीकरण} जहां \(\mu_t=R_t\) और सशर्त संभावना में संग्रहित है conv_serial_interval , नीचे परिभाषित।

अपेक्षित मौतों का मॉडल दैनिक संक्रमणों और संक्रमण और मृत्यु के बीच के दिनों के वितरण को दर्शाता है। यही कारण है, दिन पर उम्मीद से होने वाली मौतों है \(t\) के रूप में गणना की जाती है

\ begin {समीकरण} \ sum_ {i = 0} ^ {टी 1} n_i \ text {पी (दिन पर मृत्यु \(t\)| दिन पर संक्रमण \(i\))} \ अंत {समीकरण} जहां सशर्त संभावना संग्रहीत किया जाता है में conv_fatality_rate , नीचे परिभाषित।

from tensorflow_probability.python.internal import broadcast_util as bu

def predict_infections(
    intervention_indicators, population, initial_cases, mu, alpha_hier,
    conv_serial_interval, initial_days, total_days):
  """Predict the number of infections by forward-simulation.

  Args:
    intervention_indicators: Binary array of shape
      `[num_countries, total_days, num_interventions]`, in which `1` indicates
      the intervention is active in that country at that time and `0` indicates
      otherwise.
    population: Vector of length `num_countries`. Population of each country.
    initial_cases: Array of shape `[batch_size, num_countries]`. Number of cases
      in each country at the start of the simulation.
    mu: Array of shape `[batch_size, num_countries]`. Initial reproduction rate
      (R_0) by country.
    alpha_hier: Array of shape `[batch_size, num_interventions]` representing
      the effectiveness of interventions.
    conv_serial_interval: Array of shape
      `[total_days - initial_days, total_days]` output from
      `make_conv_serial_interval`. Convolution kernel for serial interval
      distribution.
    initial_days: Integer, number of sequential days to seed infections after
      the 10th death in a country. (N0 in the authors' Stan code.)
    total_days: Integer, number of days of observed data plus days to forecast.
      (N2 in the authors' Stan code.)
  Returns:
    predicted_infections: Array of shape
      `[total_days, batch_size, num_countries]`. (Batched) predicted number of
      infections over time and by country.
  """
  alpha = alpha_hier - tf.cast(np.log(1.05) / 6.0, DTYPE)

  # Multiply the effectiveness of each intervention in each country (alpha)
  # by the indicator variable for whether the intervention was active and sum
  # over interventions, yielding an array of shape
  # [total_days, batch_size, num_countries] that represents the total effectiveness of
  # all interventions in each country on each day (for a batch of data).
  linear_prediction = tf.einsum(
      'ijk,...k->j...i', intervention_indicators, alpha)

  # Adjust the reproduction rate per country downward, according to the
  # effectiveness of the interventions.
  rt = mu * tf.exp(-linear_prediction, name='reproduction_rate')

  # Initialize storage array for daily infections and seed it with initial
  # cases.
  daily_infections = tf.TensorArray(
      dtype=DTYPE, size=total_days, element_shape=initial_cases.shape)
  for i in range(initial_days):
    daily_infections = daily_infections.write(i, initial_cases)

  # Initialize cumulative cases.
  init_cumulative_infections = initial_cases * initial_days

  # Simulate forward for total_days days.
  cond = lambda i, *_: i < total_days
  def body(i, prev_daily_infections, prev_cumulative_infections):
    # The probability distribution over days j that someone infected on day i
    # caught the virus from someone infected on day j.
    p_infected_on_day = tf.gather(
        conv_serial_interval, i - initial_days, axis=0)

    # Multiply p_infected_on_day by the number previous infections each day and
    # by mu, and sum to obtain new infections on day i. Mu is adjusted by
    # the fraction of the population already infected, so that the population
    # size is the upper limit on the number of infections.
    prev_daily_infections_array = prev_daily_infections.stack()
    to_sum = prev_daily_infections_array * bu.left_justified_expand_dims_like(
        p_infected_on_day, prev_daily_infections_array)
    convolution = tf.reduce_sum(to_sum, axis=0)
    rt_adj = (
        (population - prev_cumulative_infections) / population
        ) * tf.gather(rt, i)
    new_infections = rt_adj * convolution

    # Update the prediction array and the cumulative number of infections.
    daily_infections = prev_daily_infections.write(i, new_infections)
    cumulative_infections = prev_cumulative_infections + new_infections
    return i + 1, daily_infections, cumulative_infections

  _, daily_infections_final, last_cumm_sum = tf.while_loop(
      cond, body,
      (initial_days, daily_infections, init_cumulative_infections),
      maximum_iterations=(total_days - initial_days))
  return daily_infections_final.stack()

def predict_deaths(predicted_infections, ifr_noise, conv_fatality_rate):
  """Expected number of reported deaths by country, by day.

  Args:
    predicted_infections: Array of shape
      `[total_days, batch_size, num_countries]` output from
      `predict_infections`.
    ifr_noise: Array of shape `[batch_size, num_countries]`. Noise in Infection
      Fatality Rate (IFR).
    conv_fatality_rate: Array of shape
      `[total_days - 1, total_days, num_countries]`. Convolutional kernel for
      calculating fatalities, output from `make_conv_fatality_rate`.
  Returns:
    predicted_deaths: Array of shape `[total_days, batch_size, num_countries]`.
      (Batched) predicted number of deaths over time and by country.
  """
  # Multiply the number of infections on day j by the probability of death
  # on day i given infection on day j, and sum over j. This yields the expected
  result_remainder = tf.einsum(
      'i...j,kij->k...j', predicted_infections, conv_fatality_rate) * ifr_noise

  # Concatenate the result with a vector of zeros so that the first day is
  # included.
  result_temp = 1e-15 * predicted_infections[:1]
  return tf.concat([result_temp, result_remainder], axis=0)

1.2 पैरामीटर मान से पहले

यहां हम मॉडल मापदंडों पर संयुक्त पूर्व वितरण को परिभाषित करते हैं। कई पैरामीटर मानों को स्वतंत्र माना जाता है, जैसे कि पूर्व को इस प्रकार व्यक्त किया जा सकता है:

\(\text p(\tau, y, \psi, \kappa, \mu, \alpha) = \text p(\tau)\text p(y|\tau)\text p(\psi)\text p(\kappa)\text p(\mu|\kappa)\text p(\alpha)\text p(\epsilon)\)

जिसमें:

  • \(\tau\) प्रति देश, प्रारंभिक मामलों की संख्या से अधिक घातीय वितरण के साझा दर पैरामीटर है \(y = y_1, ... y_{\text{num_countries} }\)।
  • \(\psi\) मौतों की संख्या के लिए नकारात्मक द्विपद वितरण में एक पैरामीटर है।
  • \(\kappa\) प्रत्येक देश, में प्रारंभिक प्रजनन नंबर पर HalfNormal वितरण का साझा पैमाने पैरामीटर है \(\mu = \mu_1, ..., \mu_{\text{num_countries} }\) (प्रत्येक संक्रमित व्यक्ति द्वारा प्रेषित अतिरिक्त मामलों की संख्या का संकेत है)।
  • \(\alpha = \alpha_1, ..., \alpha_6\) छह हस्तक्षेप से प्रत्येक की प्रभावशीलता है।
  • \(\epsilon\) (बुलाया ifr_noise कोड में, लेखकों 'स्टेन कोड के बाद) संक्रमण मृत्यु दर (आईएफआर) में शोर है।

हम इस मॉडल को एक टीएफपी संयुक्त वितरण के रूप में व्यक्त करते हैं, एक प्रकार का टीएफपी वितरण जो संभाव्य ग्राफिकल मॉडल की अभिव्यक्ति को सक्षम बनाता है।

def make_jd_prior(num_countries, num_interventions):
  return tfd.JointDistributionSequentialAutoBatched([
      # Rate parameter for the distribution of initial cases (tau).
      tfd.Exponential(rate=tf.cast(0.03, DTYPE)),

      # Initial cases for each country.
      lambda tau: tfd.Sample(
          tfd.Exponential(rate=tf.cast(1, DTYPE) / tau),
          sample_shape=num_countries),

      # Parameter in Negative Binomial model for deaths (psi).
      tfd.HalfNormal(scale=tf.cast(5, DTYPE)),

      # Parameter in the distribution over the initial reproduction number, R_0
      # (kappa).
      tfd.HalfNormal(scale=tf.cast(0.5, DTYPE)),

      # Initial reproduction number, R_0, for each country (mu).
      lambda kappa: tfd.Sample(
          tfd.TruncatedNormal(loc=3.28, scale=kappa, low=1e-5, high=1e5),
          sample_shape=num_countries),

      # Impact of interventions (alpha; shared for all countries).
      tfd.Sample(
          tfd.Gamma(tf.cast(0.1667, DTYPE), 1), sample_shape=num_interventions),

      # Multiplicative noise in Infection Fatality Rate.
      tfd.Sample(
          tfd.TruncatedNormal(
              loc=tf.cast(1., DTYPE), scale=0.1, low=1e-5, high=1e5),
              sample_shape=num_countries)
  ])

1.3 पैरामीटर मानों पर सशर्त मनाई गई मौतों की संभावना

संभावना मॉडल व्यक्त \(p(\text{deaths} | \tau, y, \psi, \kappa, \mu, \alpha, \epsilon)\)। यह मापदंडों पर सशर्त संक्रमणों और अपेक्षित मौतों की संख्या के लिए मॉडल लागू करता है, और मानता है कि वास्तविक मौतें एक नकारात्मक द्विपद वितरण का पालन करती हैं।

def make_likelihood_fn(
    intervention_indicators, population, deaths,
    infection_fatality_rate, initial_days, total_days):

  # Create a mask for the initial days of simulated data, as they are not
  # counted in the likelihood.
  observed_deaths = tf.constant(deaths.T[np.newaxis, ...], dtype=DTYPE)
  mask_temp = deaths != -1
  mask_temp[:, :START_DAYS] = False
  observed_deaths_mask = tf.constant(mask_temp.T[np.newaxis, ...])

  conv_serial_interval = make_conv_serial_interval(initial_days, total_days)
  conv_fatality_rate = make_conv_fatality_rate(
      infection_fatality_rate, total_days)

  def likelihood_fn(tau, initial_cases, psi, kappa, mu, alpha_hier, ifr_noise):
    # Run models for infections and expected deaths
    predicted_infections = predict_infections(
        intervention_indicators, population, initial_cases, mu, alpha_hier,
        conv_serial_interval, initial_days, total_days)
    e_deaths_all_countries = predict_deaths(
        predicted_infections, ifr_noise, conv_fatality_rate)

    # Construct the Negative Binomial distribution for deaths by country.
    mu_m = tf.transpose(e_deaths_all_countries, [1, 0, 2])
    psi_m = psi[..., tf.newaxis, tf.newaxis]
    probs = tf.clip_by_value(mu_m / (mu_m + psi_m), 1e-9, 1.)
    likelihood_elementwise = tfd.NegativeBinomial(
        total_count=psi_m, probs=probs).log_prob(observed_deaths)
    return tf.reduce_sum(
        tf.where(observed_deaths_mask,
                likelihood_elementwise,
                tf.zeros_like(likelihood_elementwise)),
        axis=[-2, -1])

  return likelihood_fn

1.4 संक्रमण से मौत की संभावना

यह खंड संक्रमण के बाद के दिनों में होने वाली मौतों के वितरण की गणना करता है। यह मानता है कि संक्रमण से मृत्यु तक का समय दो गामा-भिन्न मात्राओं का योग है, जो संक्रमण से बीमारी की शुरुआत और शुरुआत से मृत्यु तक के समय का प्रतिनिधित्व करता है। समय-मौत वितरण से संक्रमण मृत्यु दर डेटा के साथ संयुक्त है वेरिटी एट अल। (2020) संक्रमण के बाद के दिनों में मौत की संभावना की गणना करने के।

def daily_fatality_probability(infection_fatality_rate, total_days):
  """Computes the probability of death `d` days after infection."""

  # Convert from alternative Gamma parametrization and construct distributions
  # for number of days from infection to onset and onset to death.
  concentration1 = tf.cast((1. / 0.86)**2, DTYPE)
  rate1 = concentration1 / 5.1
  concentration2 = tf.cast((1. / 0.45)**2, DTYPE)
  rate2 = concentration2 / 18.8
  infection_to_onset = tfd.Gamma(concentration=concentration1, rate=rate1)
  onset_to_death = tfd.Gamma(concentration=concentration2, rate=rate2)

  # Create empirical distribution for number of days from infection to death.
  inf_to_death_dist = tfd.Empirical(
      infection_to_onset.sample([5e6]) + onset_to_death.sample([5e6]))

  # Subtract the CDF value at day i from the value at day i + 1 to compute the
  # probability of death on day i given infection on day 0, and given that
  # death (not recovery) is the outcome.
  times = np.arange(total_days + 1., dtype=DTYPE) + 0.5
  cdf = inf_to_death_dist.cdf(times).numpy()
  f_before_ifr = cdf[1:] - cdf[:-1]
  # Explicitly set the zeroth value to the empirical cdf at time 1.5, to include
  # the mass between time 0 and time .5.
  f_before_ifr[0] = cdf[1]

  # Multiply the daily fatality rates conditional on infection and eventual
  # death (f_before_ifr) by the infection fatality rates (probability of death
  # given intection) to obtain the probability of death on day i conditional
  # on infection on day 0.
  return infection_fatality_rate[..., np.newaxis] * f_before_ifr

def make_conv_fatality_rate(infection_fatality_rate, total_days):
  """Computes the probability of death on day `i` given infection on day `j`."""
  p_fatal_all_countries = daily_fatality_probability(
      infection_fatality_rate, total_days)

  # Use the probability of death d days after infection in each country
  # to build an array of shape [total_days - 1, total_days, num_countries],
  # where the element [i, j, c] is the probability of death on day i+1 given
  # infection on day j in country c.
  conv_fatality_rate = np.zeros(
      [total_days - 1, total_days, p_fatal_all_countries.shape[0]])
  for n in range(1, total_days):
    conv_fatality_rate[n - 1, 0:n, :] = (
        p_fatal_all_countries[:, n - 1::-1]).T
  return tf.constant(conv_fatality_rate, dtype=DTYPE)

1.5 सीरियल अंतराल

सीरियल अंतराल रोग संचरण की एक श्रृंखला में लगातार मामलों के बीच का समय है, और माना जाता है कि गामा वितरित किया जाता है। हम धारावाहिक अंतराल वितरण का उपयोग संभावना है कि दिन पर संक्रमित व्यक्ति की गणना करने के \(i\) पहले दिन पर संक्रमित व्यक्ति से वायरस पकड़ा \(j\) ( conv_serial_interval को तर्क predict_infections )।

def make_conv_serial_interval(initial_days, total_days):
  """Construct the convolutional kernel for infection timing."""

  g = tfd.Gamma(tf.cast(1. / (0.62**2), DTYPE), 1./(6.5*0.62**2))
  g_cdf = g.cdf(np.arange(total_days, dtype=DTYPE))

  # Approximate the probability mass function for the number of days between
  # successive infections.
  serial_interval = g_cdf[1:] - g_cdf[:-1]

  # `conv_serial_interval` is an array of shape
  # [total_days - initial_days, total_days] in which entry [i, j] contains the
  # probability that an individual infected on day i + initial_days caught the
  # virus from someone infected on day j.
  conv_serial_interval = np.zeros([total_days - initial_days, total_days])
  for n in range(initial_days, total_days):
    conv_serial_interval[n - initial_days, 0:n] = serial_interval[n - 1::-1]
  return tf.constant(conv_serial_interval, dtype=DTYPE)

2 डेटा प्रीप्रोसेसिंग

COUNTRIES = [
    'Austria',
    'Belgium',
    'Denmark',
    'France',
    'Germany',
    'Italy',
    'Norway',
    'Spain',
    'Sweden',
    'Switzerland',
    'United_Kingdom'
]

2.1 हस्तक्षेप डेटा प्राप्त करें और प्रीप्रोसेस करें

2.2 केस/मृत्यु डेटा प्राप्त करें और हस्तक्षेपों में शामिल हों

2.3 संक्रमित मृत्यु अनुपात और जनसंख्या डेटा प्राप्त करें और संसाधित करें

2.4 देश-विशिष्ट डेटा प्रीप्रोसेस करें

# Model up to 75 days of data for each country, starting 30 days before the
# tenth cumulative death.
START_DAYS = 30
MAX_DAYS = 102
COVARIATE_COLUMNS = any_intervention_list + ['any_intervention']

# Initialize an array for number of deaths.
deaths = -np.ones((num_countries, MAX_DAYS), dtype=DTYPE)

# Assuming every intervention is still inplace in the unobserved future
num_interventions = len(COVARIATE_COLUMNS)
intervention_indicators = np.ones((num_countries, MAX_DAYS, num_interventions))

first_days = {}
for i, c in enumerate(COUNTRIES):
  c_data = data.loc[c]

  # Include data only after 10th death in a country.
  mask = c_data['deaths'].cumsum() >= 10

  # Get the date that the epidemic starts in a country.
  first_day = c_data.index[mask][0] - pd.to_timedelta(START_DAYS, 'days')
  c_data = c_data.truncate(before=first_day)

  # Truncate the data after 28 March 2020 for comparison with Flaxman et al.
  c_data = c_data.truncate(after='2020-03-28')

  c_data = c_data.iloc[:MAX_DAYS]
  days_of_data = c_data.shape[0]
  deaths[i, :days_of_data] = c_data['deaths']
  intervention_indicators[i, :days_of_data] = c_data[
    COVARIATE_COLUMNS].to_numpy()
  first_days[c] = first_day

# Number of sequential days to seed infections after the 10th death in a
# country. (N0 in authors' Stan code.)
INITIAL_DAYS = 6

# Number of days of observed data plus days to forecast. (N2 in authors' Stan
# code.)
TOTAL_DAYS = deaths.shape[1]

3 मॉडल अनुमान

फ्लैक्समैन एट अल। (2020) का इस्तेमाल किया स्टेन Hamiltonian मोंटे कार्लो (एचएमसी) और नो-यू-टर्न नमूना (पागल) के साथ पैरामीटर पीछे से नमूना करने के लिए।

यहां, हम एचएमसी को दोहरे औसत चरण आकार अनुकूलन के साथ लागू करते हैं। हम पूर्व शर्त और आरंभीकरण के लिए एचएमसी के एक पायलट रन का उपयोग करते हैं।

GPU पर कुछ ही मिनटों में अनुमान चलता है।

3.1 मॉडल के लिए पूर्व और संभावना का निर्माण करें

jd_prior = make_jd_prior(num_countries, num_interventions)
likelihood_fn = make_likelihood_fn(
    intervention_indicators, population_value, deaths,
    infection_fatality_rate, INITIAL_DAYS, TOTAL_DAYS)

3.2 उपयोगिताएँ

def get_bijectors_from_samples(samples, unconstraining_bijectors, batch_axes):
  """Fit bijectors to the samples of a distribution.

  This fits a diagonal covariance multivariate Gaussian transformed by the
  `unconstraining_bijectors` to the provided samples. The resultant
  transformation can be used to precondition MCMC and other inference methods.
  """
  state_std = [    
      tf.math.reduce_std(bij.inverse(x), axis=batch_axes)
      for x, bij in zip(samples, unconstraining_bijectors)
  ]
  state_mu = [
      tf.math.reduce_mean(bij.inverse(x), axis=batch_axes)
      for x, bij in zip(samples, unconstraining_bijectors)
  ]
  return [tfb.Chain([cb, tfb.Shift(sh), tfb.Scale(sc)])
          for cb, sh, sc in zip(unconstraining_bijectors, state_mu, state_std)]

def generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors):
  """Creates an initial MCMC state, and bijectors from the prior."""
  prior_samples = jd_prior.sample(4096)

  bijectors = get_bijectors_from_samples(
      prior_samples, unconstraining_bijectors, batch_axes=0)

  init_state = [
    bij(tf.zeros([nchain] + list(s), DTYPE))
    for s, bij in zip(jd_prior.event_shape, bijectors)
  ]

  return init_state, bijectors

@tf.function(autograph=False, experimental_compile=True)
def sample_hmc(
    init_state,
    step_size,
    target_log_prob_fn,
    unconstraining_bijectors,
    num_steps=500,
    burnin=50,
    num_leapfrog_steps=10):

    def trace_fn(_, pkr):
        return {
            'target_log_prob': pkr.inner_results.inner_results.accepted_results.target_log_prob,
            'diverging': ~(pkr.inner_results.inner_results.log_accept_ratio > -1000.),
            'is_accepted': pkr.inner_results.inner_results.is_accepted,
            'step_size': [tf.exp(s) for s in pkr.log_averaging_step],
        }

    hmc = tfp.mcmc.HamiltonianMonteCarlo(
        target_log_prob_fn,
        step_size=step_size,
        num_leapfrog_steps=num_leapfrog_steps)

    hmc = tfp.mcmc.TransformedTransitionKernel(
        inner_kernel=hmc,
        bijector=unconstraining_bijectors)

    hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
        hmc,
        num_adaptation_steps=int(burnin * 0.8),
        target_accept_prob=0.8,
        decay_rate=0.5)

    # Sampling from the chain.
    return tfp.mcmc.sample_chain(
        num_results=burnin + num_steps,
        current_state=init_state,
        kernel=hmc,
        trace_fn=trace_fn)

3.3 इवेंट स्पेस बायजेक्टर को परिभाषित करें

एचएमसी सबसे कुशल जब एक समदैशिक मल्टीवेरिएट गाऊसी वितरण से नमूना है ( Mangoubi और स्मिथ (2017) ), इसलिए पहला कदम है कि संभव के रूप में की तरह जितना देखो करने के लिए लक्ष्य घनत्व पूर्व शर्त है।

सबसे पहले और सबसे महत्वपूर्ण, हम विवश (जैसे, गैर-नकारात्मक) चर को एक अप्रतिबंधित स्थान में बदलते हैं, जिसकी एचएमसी को आवश्यकता होती है। इसके अतिरिक्त, हम परिवर्तित लक्ष्य घनत्व की पूंछ के भारीपन में हेरफेर करने के लिए सिंहआर्कसिंह बिजेक्टर को नियोजित करते हैं; हम इन के रूप में मोटे तौर पर गिर करना चाहते हैं \(e^{-x^2}\)।

unconstraining_bijectors = [
    tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # tau
    tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # initial_cases
    tfb.Softplus(), # psi
    tfb.Softplus(), # kappa
    tfb.Softplus(), # mu
    tfb.Chain([tfb.Scale(tf.constant(0.4, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(skewness=tf.constant(-0.2, DTYPE), tailweight=tf.constant(2., DTYPE))]), # alpha
    tfb.Softplus(), # ifr_noise
]

3.4 एचएमसी पायलट रन

हम पहले एचएमसी को पूर्व शर्त से चलाते हैं, जिसे 0 से शुरू किया गया है। हम चेन को इनिशियलाइज़ करने के लिए पहले के नमूनों का उपयोग नहीं करते हैं क्योंकि व्यवहार में वे अक्सर खराब संख्या के कारण अटकी हुई जंजीरों में परिणत होते हैं।

%%time

nchain = 32

target_log_prob_fn = lambda *x: jd_prior.log_prob(*x) + likelihood_fn(*x)
init_state, bijectors = generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors)

# Each chain gets its own step size.
step_size = [tf.fill([nchain] + [1] * (len(s.shape) - 1), tf.constant(0.01, DTYPE)) for s in init_state]

burnin = 200
num_steps = 100

pilot_samples, pilot_sampler_stat = sample_hmc(
    init_state,
    step_size,
    target_log_prob_fn,
    bijectors,
    num_steps=num_steps,
    burnin=burnin,
    num_leapfrog_steps=10)

CPU times: user 56.8 s, sys: 2.34 s, total: 59.1 s
Wall time: 1min 1s

3.5 पायलट नमूनों की कल्पना करें

हम अटकी हुई जंजीरों और नेत्रगोलक अभिसरण की तलाश कर रहे हैं। हम यहां औपचारिक निदान कर सकते हैं, लेकिन यह अति आवश्यक नहीं है क्योंकि यह सिर्फ एक पायलट रन है।

import arviz as az
az.style.use('arviz-darkgrid')

var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']

pilot_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
                     for k, v in zip(var_name, pilot_samples)}

हम वार्मअप के दौरान विचलन का निरीक्षण करते हैं, मुख्यतः क्योंकि दोहरे औसत चरण आकार अनुकूलन इष्टतम चरण आकार के लिए एक बहुत ही आक्रामक खोज का उपयोग करता है। एक बार अनुकूलन बंद हो जाने पर, विचलन भी गायब हो जाते हैं।

az_trace = az.from_dict(posterior=pilot_with_warmup,
                        sample_stats={'diverging': np.swapaxes(pilot_sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));

पीएनजी

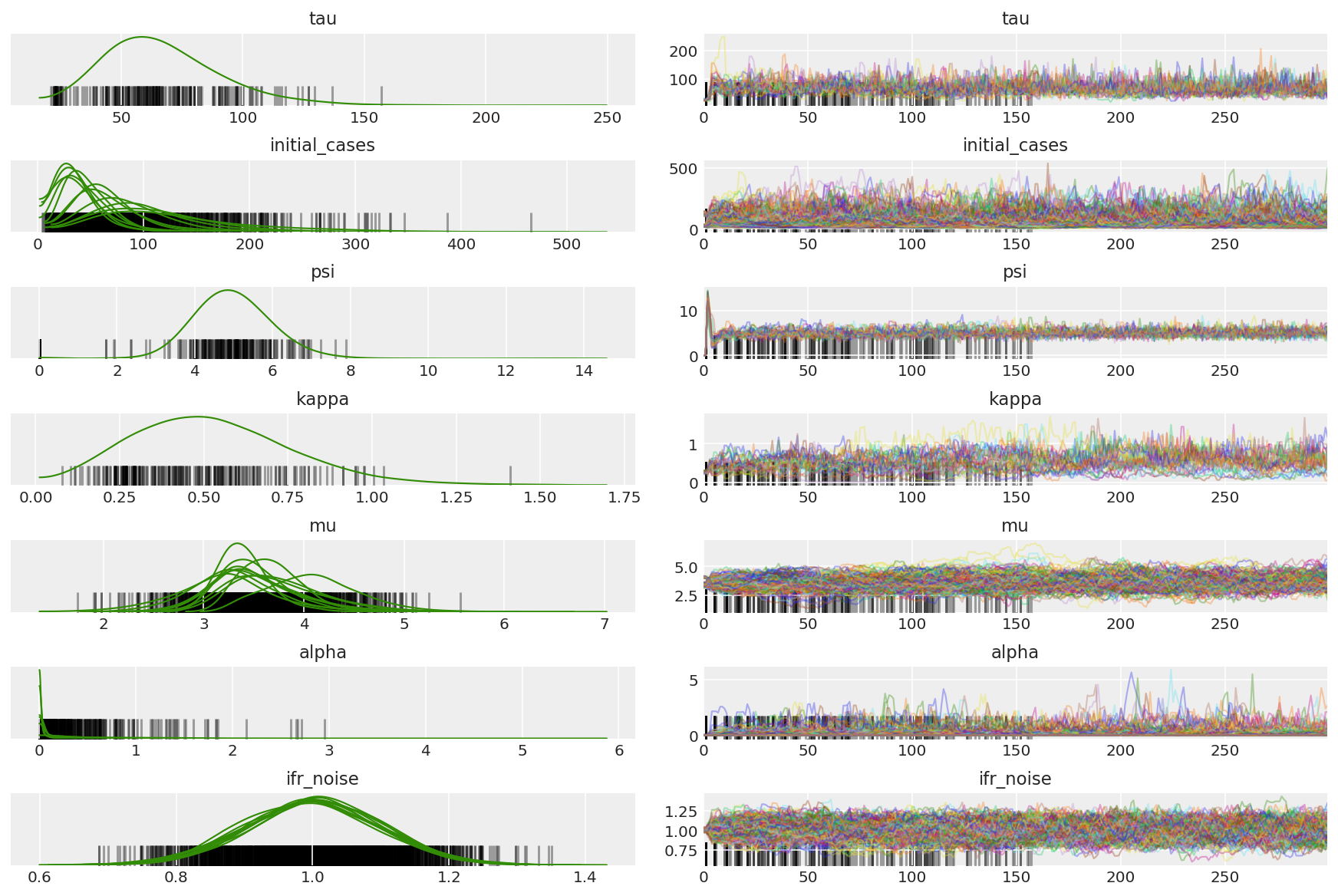
plt.plot(pilot_sampler_stat['step_size'][0]);

पीएनजी

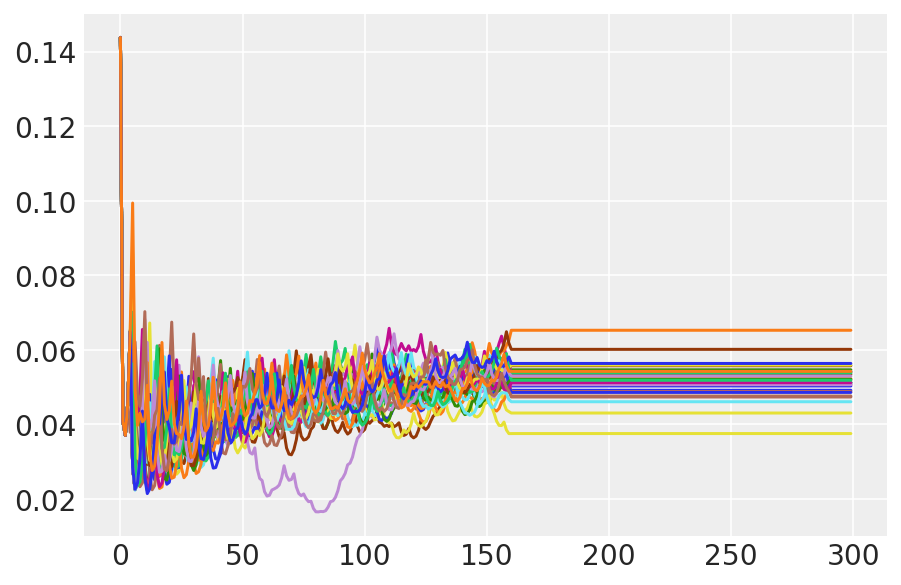
3.6 एचएमसी चलाएं

सिद्धांत रूप में हम अंतिम विश्लेषण के लिए पायलट नमूनों का उपयोग कर सकते हैं (यदि हम इसे अभिसरण प्राप्त करने के लिए अधिक समय तक चलाते हैं), लेकिन यह एक और एचएमसी रन शुरू करने के लिए थोड़ा अधिक कुशल है, इस बार पायलट नमूनों द्वारा पूर्व शर्त और प्रारंभ किया गया है।

%%time

burnin = 50
num_steps = 200

bijectors = get_bijectors_from_samples([s[burnin:] for s in pilot_samples],
                                       unconstraining_bijectors=unconstraining_bijectors,
                                       batch_axes=(0, 1))

samples, sampler_stat = sample_hmc(
    [s[-1] for s in pilot_samples],
    [s[-1] for s in pilot_sampler_stat['step_size']],
    target_log_prob_fn,
    bijectors,
    num_steps=num_steps,
    burnin=burnin,
    num_leapfrog_steps=20)

CPU times: user 1min 26s, sys: 3.88 s, total: 1min 30s
Wall time: 1min 32s

plt.plot(sampler_stat['step_size'][0]);

पीएनजी

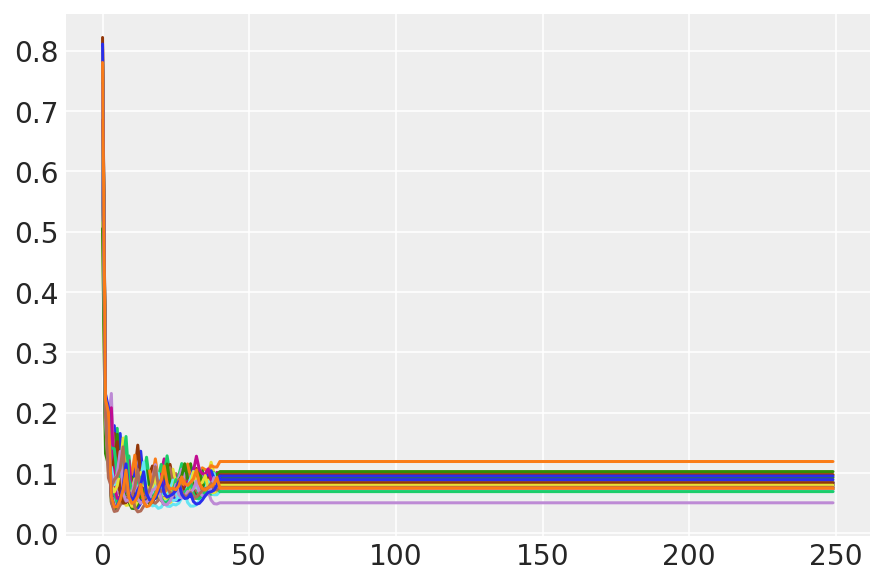
3.7 नमूनों की कल्पना करें

import arviz as az
az.style.use('arviz-darkgrid')

var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']

posterior = {k: np.swapaxes(v.numpy()[burnin:], 1, 0)
             for k, v in zip(var_name, samples)}
posterior_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
             for k, v in zip(var_name, samples)}

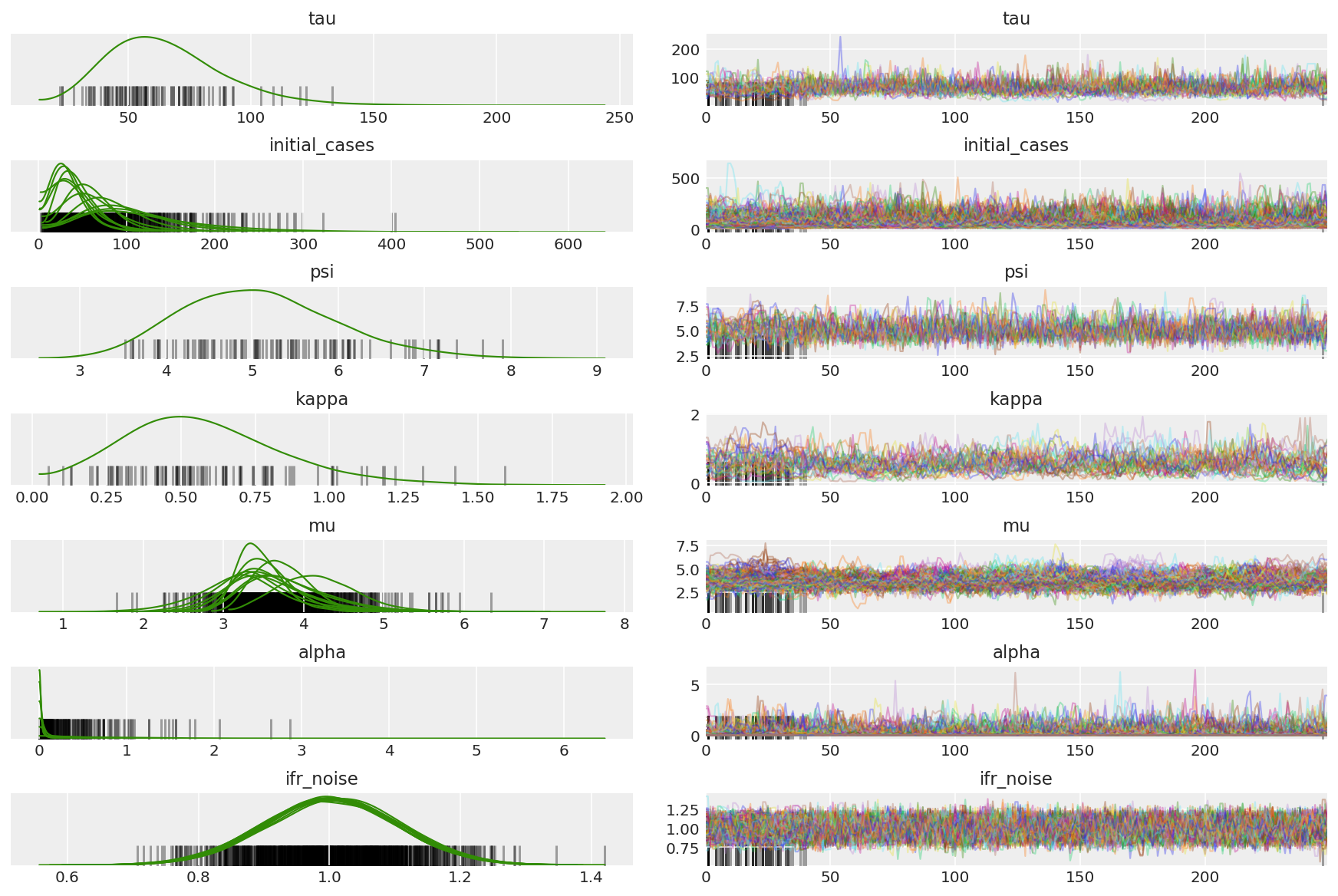
जंजीरों के सारांश की गणना करें। हम 1 के करीब उच्च ESS और r_hat की तलाश कर रहे हैं।

az.summary(posterior)

az_trace = az.from_dict(posterior=posterior_with_warmup,
                        sample_stats={'diverging': np.swapaxes(sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));

पीएनजी

सभी आयामों में ऑटो-सहसंबंध कार्यों को देखना शिक्षाप्रद है। हम ऐसे कार्यों की तलाश कर रहे हैं जो जल्दी से नीचे जाते हैं, लेकिन इतना नहीं कि वे नकारात्मक में चले जाते हैं (जो कि एचएमसी के प्रतिध्वनि से टकराने का संकेत है, जो कि एर्गोडिसिटी के लिए बुरा है और पूर्वाग्रह का परिचय दे सकता है)।

with az.rc_context(rc={'plot.max_subplots': None}):
  az.plot_autocorr(posterior, combined=True, figsize=(12, 16), textsize=12);

पीएनजी

4 परिणाम

निम्नलिखित भूखंडों से अधिक पीछे भविष्य कहनेवाला वितरण का विश्लेषण \(R_t\), मौतों की संख्या, और संक्रमण, Flaxman एट अल में विश्लेषण के लिए इसी तरह की संख्या। (2020)।

total_num_samples = np.prod(posterior['mu'].shape[:2])

# Calculate R_t given parameter estimates.
def rt_samples_batched(mu, intervention_indicators, alpha):
  linear_prediction = tf.reduce_sum(
      intervention_indicators * alpha[..., np.newaxis, np.newaxis, :], axis=-1)
  rt_hat = mu[..., tf.newaxis] * tf.exp(-linear_prediction, name='rt')
  return rt_hat

alpha_hat = tf.convert_to_tensor(
    posterior['alpha'].reshape(total_num_samples, posterior['alpha'].shape[-1]))
mu_hat = tf.convert_to_tensor(
    posterior['mu'].reshape(total_num_samples, num_countries))
rt_hat = rt_samples_batched(mu_hat, intervention_indicators, alpha_hat)
sampled_initial_cases = posterior['initial_cases'].reshape(
    total_num_samples, num_countries)
sampled_ifr_noise = posterior['ifr_noise'].reshape(
    total_num_samples, num_countries)
psi_hat = posterior['psi'].reshape([total_num_samples])

conv_serial_interval = make_conv_serial_interval(INITIAL_DAYS, TOTAL_DAYS)
conv_fatality_rate = make_conv_fatality_rate(infection_fatality_rate, TOTAL_DAYS)
pred_hat = predict_infections(
    intervention_indicators, population_value, sampled_initial_cases, mu_hat,
    alpha_hat, conv_serial_interval, INITIAL_DAYS, TOTAL_DAYS)
expected_deaths = predict_deaths(pred_hat, sampled_ifr_noise, conv_fatality_rate)

psi_m = psi_hat[np.newaxis, ..., np.newaxis]
probs = tf.clip_by_value(expected_deaths / (expected_deaths + psi_m), 1e-9, 1.)
predicted_deaths = tfd.NegativeBinomial(
    total_count=psi_m, probs=probs).sample()

# Predict counterfactual infections/deaths in the absence of interventions
no_intervention_infections = predict_infections(
    intervention_indicators,
    population_value,
    sampled_initial_cases,
    mu_hat,
    tf.zeros_like(alpha_hat),
    conv_serial_interval,
    INITIAL_DAYS, TOTAL_DAYS)

no_intervention_expected_deaths = predict_deaths(
    no_intervention_infections, sampled_ifr_noise, conv_fatality_rate)
probs = tf.clip_by_value(
    no_intervention_expected_deaths / (no_intervention_expected_deaths + psi_m),
    1e-9, 1.)
no_intervention_predicted_deaths = tfd.NegativeBinomial(
    total_count=psi_m, probs=probs).sample()

4.1 हस्तक्षेपों की प्रभावशीलता

फ्लैक्समैन एट अल के चित्र 4 के समान। (2020)।

def intervention_effectiveness(alpha):

  alpha_adj = 1. - np.exp(-alpha + np.log(1.05) / 6.)
  alpha_adj_first = (
      1. - np.exp(-alpha - alpha[..., -1:] + np.log(1.05) / 6.))

  fig, ax = plt.subplots(1, 1, figsize=[12, 6])
  intervention_perm = [2, 1, 3, 4, 0]
  percentile_vals = [2.5, 97.5]
  jitter = .2

  for ind in range(5):
    first_low, first_high = tfp.stats.percentile(
        alpha_adj_first[..., ind], percentile_vals)
    low, high = tfp.stats.percentile(
        alpha_adj[..., ind], percentile_vals)

    p_ind = intervention_perm[ind]
    ax.hlines(p_ind, low, high, label='Later Intervention', colors='g')
    ax.scatter(alpha_adj[..., ind].mean(), p_ind, color='g')
    ax.hlines(p_ind + jitter, first_low, first_high,
              label='First Intervention', colors='r')
    ax.scatter(alpha_adj_first[..., ind].mean(), p_ind + jitter, color='r')

    if ind == 0:
      plt.legend(loc='lower right')
  ax.set_yticks(range(5))
  ax.set_yticklabels(
      [any_intervention_list[intervention_perm.index(p)] for p in range(5)])
  ax.set_xlim([-0.01, 1.])
  r = fig.patch
  r.set_facecolor('white') 

intervention_effectiveness(alpha_hat)

पीएनजी

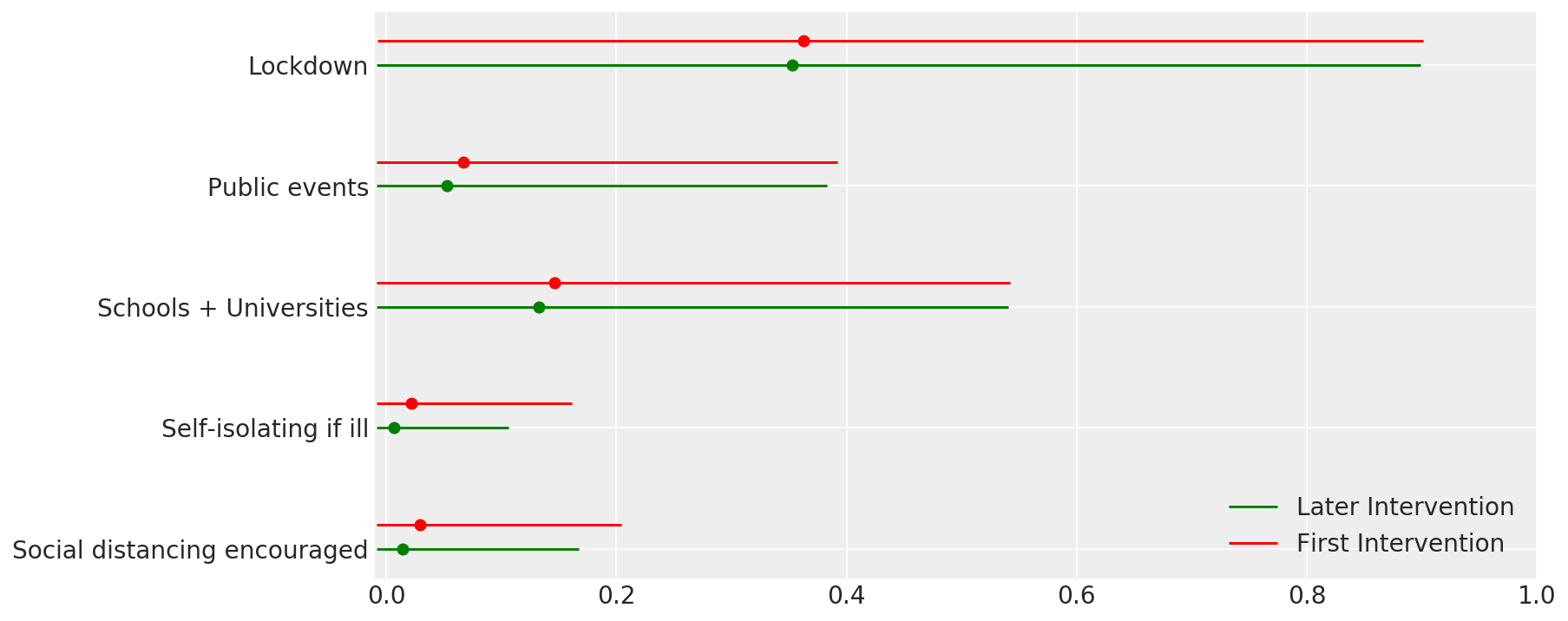
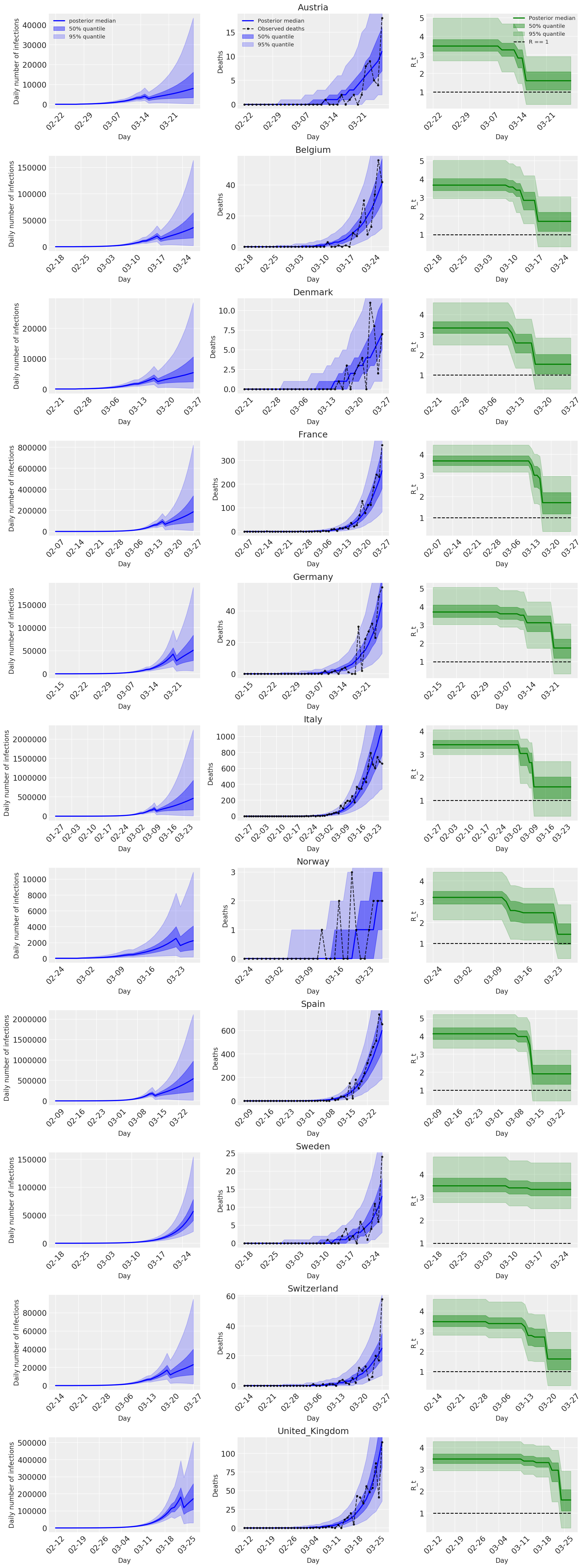
4.2 संक्रमण, मृत्यु, और देश के अनुसार R_t

फ्लैक्समैन एट अल के चित्र 2 के समान। (2020)।

पीएनजी

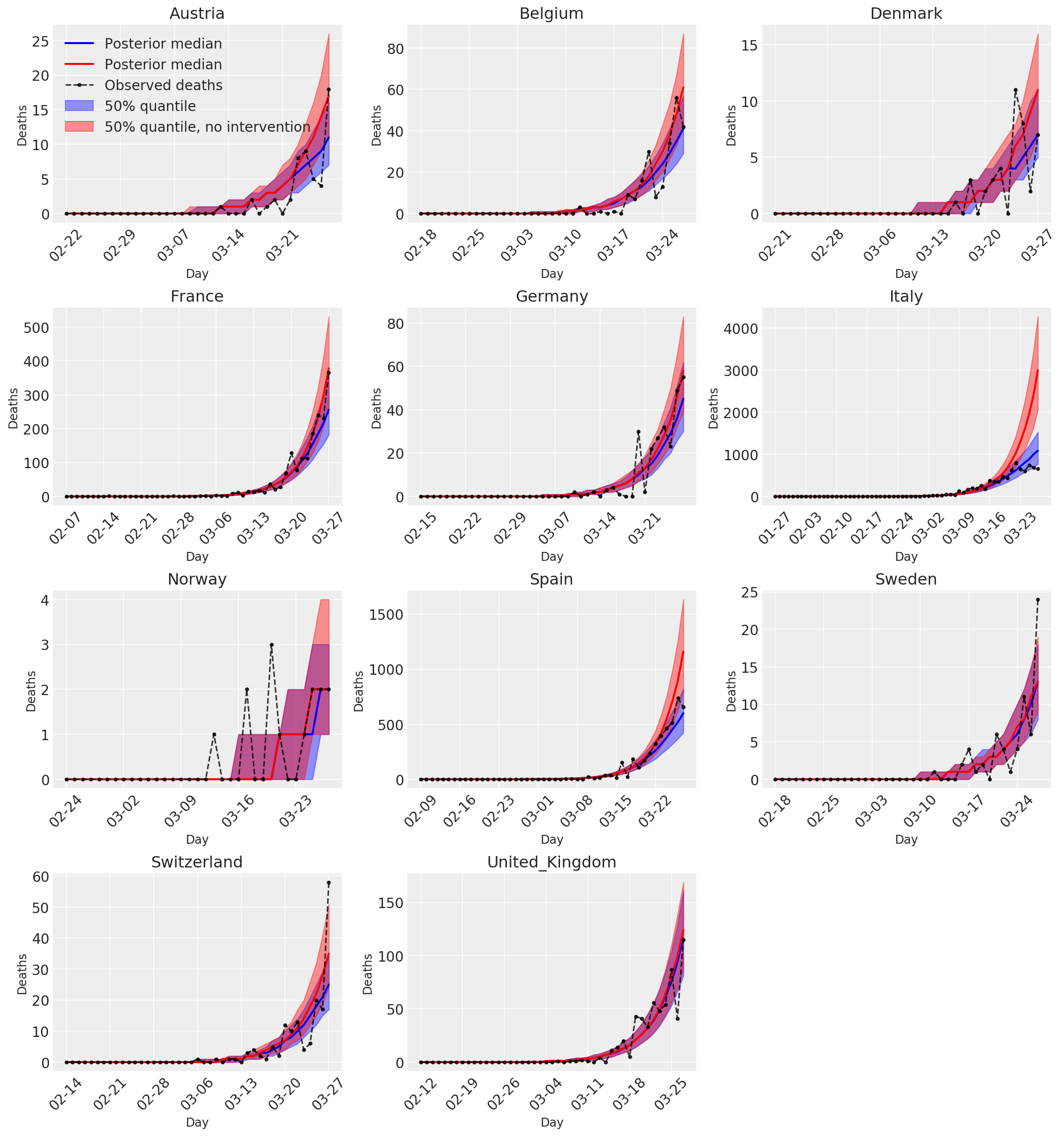
4.3 हस्तक्षेप के साथ और बिना पूर्वानुमानित/पूर्वानुमानित मौतों की दैनिक संख्या

पीएनजी