انتشار نمذجة COVID-19 في أوروبا وتأثير التدخلات

مرخصة بموجب ترخيص معهد ماساتشوستس للتكنولوجيا

عرض على TensorFlow.org تشغيل في Google Colab عرض المصدر على جيثب تحميل دفتر

لإبطاء انتشار COVID-19 في أوائل عام 2020 ، تبنت الدول الأوروبية تدخلات غير صيدلانية مثل إغلاق الشركات غير الأساسية ، وعزل الحالات الفردية ، وحظر السفر ، وغيرها من التدابير لتشجيع التباعد الاجتماعي. حلل فريق الاستجابة الكلية الملكية COVID 19 فعالية هذه التدابير في ورقتهم "تقدير عدد الإصابات وتأثير التدخلات غير الدوائية على COVID-19 في 11 بلدا أوروبيا" ، وذلك باستخدام نموذج النظرية الافتراضية الهرمية جنبا إلى جنب مع ميكانيكي نموذج وبائي.

يحتوي هذا Colab على تنفيذ احتمالية TensorFlow (TFP) لهذا التحليل ، منظم على النحو التالي:

  • يحدد "إعداد النموذج" النموذج الوبائي لانتقال المرض والوفيات الناتجة ، والتوزيع البايزي المسبق على معلمات النموذج ، وتوزيع عدد الوفيات المشروطة بقيم المعلمات.
  • تحمل "المعالجة المسبقة للبيانات" البيانات المتعلقة بتوقيت ونوع التدخلات في كل بلد ، وتعداد الوفيات بمرور الوقت ، ومعدلات الوفيات المقدرة للمصابين.
  • "الاستدلال النموذجي" يبني نموذجًا هرميًا بايزي ويدير هاميلتونيان مونت كارلو (HMC) لأخذ عينات من التوزيع اللاحق عبر المعلمات.
  • تُظهر "النتائج" التوزيعات التنبؤية اللاحقة لكميات الاهتمام مثل الوفيات المتوقعة والوفيات الواقعية في غياب التدخلات.

ووجدت ورقة أدلة على أن البلدان قد تمكنت من خفض عدد الإصابات الجديدة تنتقل عن طريق كل شخص مصاب (\(R_t\))، ولكن أن فترات موثوقة الواردة \(R_t=1\) (القيمة أعلاه والتي استمر الوباء في الانتشار) وأنه من السابق لأوانه لاستخلاص استنتاجات قوية حول فعالية التدخلات. رمز ستان للورقة في المؤلفين جيثب مستودع، وهذا Colab يستنسخ الإصدار 2 .

pip3 install -q git+git://github.com/arviz-devs/arviz.git
pip3 install -q tf-nightly tfp-nightly

الواردات

1 إعداد النموذج

1.1 نموذج آلي للعدوى والوفيات

نموذج العدوى يحاكي عدد الإصابات في كل بلد بمرور الوقت. بيانات المدخلات هي توقيت ونوع التدخلات وحجم السكان والحالات الأولية. تتحكم المعلمات في فعالية التدخلات ومعدل انتقال المرض. يطبق نموذج العدد المتوقع للوفيات معدل الوفيات على الإصابات المتوقعة.

يقوم نموذج الإصابة بإجراء التفاف للعدوى اليومية السابقة بالتوزيع المتسلسل للفاصل الزمني (التوزيع على عدد الأيام بين الإصابة وإصابة شخص آخر). في كل خطوة الوقت، وعدد الإصابات الجديدة في وقت \(t\)، \(n_t\)، تحسب على النحو

\ ابدأ {المعادلة} \ sum_ {i = 0} ^ {t-1} n_i \ mu_t \ text {p} (\ text {تم التقاطه من شخص مصاب في} i | \ text {مصاب حديثًا في} t) \ end { المعادلة} حيث \(\mu_t=R_t\) يتم تخزين والاحتمال الشرطي في conv_serial_interval ، هو موضح أدناه.

يقوم نموذج الوفيات المتوقعة بعمل التفاف للعدوى اليومية وتوزيع الأيام بين العدوى والوفاة. و، أن الوفيات المتوقع في يوم \(t\) تحسب على النحو

\ تبدأ {المعادلة} \ sum_ {ط = 0} ^ {ر 1} n_i \ النص {ص (الموت في يوم \(t\)| العدوى في يوم \(i\))} \ نهاية {المعادلة} حيث يتم تخزين الاحتمال الشرطي في conv_fatality_rate ، هو موضح أدناه.

from tensorflow_probability.python.internal import broadcast_util as bu

def predict_infections(
    intervention_indicators, population, initial_cases, mu, alpha_hier,
    conv_serial_interval, initial_days, total_days):
  """Predict the number of infections by forward-simulation.

  Args:
    intervention_indicators: Binary array of shape
      `[num_countries, total_days, num_interventions]`, in which `1` indicates
      the intervention is active in that country at that time and `0` indicates
      otherwise.
    population: Vector of length `num_countries`. Population of each country.
    initial_cases: Array of shape `[batch_size, num_countries]`. Number of cases
      in each country at the start of the simulation.
    mu: Array of shape `[batch_size, num_countries]`. Initial reproduction rate
      (R_0) by country.
    alpha_hier: Array of shape `[batch_size, num_interventions]` representing
      the effectiveness of interventions.
    conv_serial_interval: Array of shape
      `[total_days - initial_days, total_days]` output from
      `make_conv_serial_interval`. Convolution kernel for serial interval
      distribution.
    initial_days: Integer, number of sequential days to seed infections after
      the 10th death in a country. (N0 in the authors' Stan code.)
    total_days: Integer, number of days of observed data plus days to forecast.
      (N2 in the authors' Stan code.)
  Returns:
    predicted_infections: Array of shape
      `[total_days, batch_size, num_countries]`. (Batched) predicted number of
      infections over time and by country.
  """
  alpha = alpha_hier - tf.cast(np.log(1.05) / 6.0, DTYPE)

  # Multiply the effectiveness of each intervention in each country (alpha)
  # by the indicator variable for whether the intervention was active and sum
  # over interventions, yielding an array of shape
  # [total_days, batch_size, num_countries] that represents the total effectiveness of
  # all interventions in each country on each day (for a batch of data).
  linear_prediction = tf.einsum(
      'ijk,...k->j...i', intervention_indicators, alpha)

  # Adjust the reproduction rate per country downward, according to the
  # effectiveness of the interventions.
  rt = mu * tf.exp(-linear_prediction, name='reproduction_rate')

  # Initialize storage array for daily infections and seed it with initial
  # cases.
  daily_infections = tf.TensorArray(
      dtype=DTYPE, size=total_days, element_shape=initial_cases.shape)
  for i in range(initial_days):
    daily_infections = daily_infections.write(i, initial_cases)

  # Initialize cumulative cases.
  init_cumulative_infections = initial_cases * initial_days

  # Simulate forward for total_days days.
  cond = lambda i, *_: i < total_days
  def body(i, prev_daily_infections, prev_cumulative_infections):
    # The probability distribution over days j that someone infected on day i
    # caught the virus from someone infected on day j.
    p_infected_on_day = tf.gather(
        conv_serial_interval, i - initial_days, axis=0)

    # Multiply p_infected_on_day by the number previous infections each day and
    # by mu, and sum to obtain new infections on day i. Mu is adjusted by
    # the fraction of the population already infected, so that the population
    # size is the upper limit on the number of infections.
    prev_daily_infections_array = prev_daily_infections.stack()
    to_sum = prev_daily_infections_array * bu.left_justified_expand_dims_like(
        p_infected_on_day, prev_daily_infections_array)
    convolution = tf.reduce_sum(to_sum, axis=0)
    rt_adj = (
        (population - prev_cumulative_infections) / population
        ) * tf.gather(rt, i)
    new_infections = rt_adj * convolution

    # Update the prediction array and the cumulative number of infections.
    daily_infections = prev_daily_infections.write(i, new_infections)
    cumulative_infections = prev_cumulative_infections + new_infections
    return i + 1, daily_infections, cumulative_infections

  _, daily_infections_final, last_cumm_sum = tf.while_loop(
      cond, body,
      (initial_days, daily_infections, init_cumulative_infections),
      maximum_iterations=(total_days - initial_days))
  return daily_infections_final.stack()

def predict_deaths(predicted_infections, ifr_noise, conv_fatality_rate):
  """Expected number of reported deaths by country, by day.

  Args:
    predicted_infections: Array of shape
      `[total_days, batch_size, num_countries]` output from
      `predict_infections`.
    ifr_noise: Array of shape `[batch_size, num_countries]`. Noise in Infection
      Fatality Rate (IFR).
    conv_fatality_rate: Array of shape
      `[total_days - 1, total_days, num_countries]`. Convolutional kernel for
      calculating fatalities, output from `make_conv_fatality_rate`.
  Returns:
    predicted_deaths: Array of shape `[total_days, batch_size, num_countries]`.
      (Batched) predicted number of deaths over time and by country.
  """
  # Multiply the number of infections on day j by the probability of death
  # on day i given infection on day j, and sum over j. This yields the expected
  result_remainder = tf.einsum(
      'i...j,kij->k...j', predicted_infections, conv_fatality_rate) * ifr_noise

  # Concatenate the result with a vector of zeros so that the first day is
  # included.
  result_temp = 1e-15 * predicted_infections[:1]
  return tf.concat([result_temp, result_remainder], axis=0)

1.2 قبل قيم المعلمات

نحدد هنا التوزيع المسبق المشترك على معلمات النموذج. يُفترض أن تكون العديد من قيم المعلمات مستقلة ، بحيث يمكن التعبير عن السابقة على النحو التالي:

\(\text p(\tau, y, \psi, \kappa, \mu, \alpha) = \text p(\tau)\text p(y|\tau)\text p(\psi)\text p(\kappa)\text p(\mu|\kappa)\text p(\alpha)\text p(\epsilon)\)

بحيث:

  • \(\tau\) هي المعلمة معدل المشتركة للتوزيع الأسي على مدى عدد من الحالات الأولية لكل بلد، \(y = y_1, ... y_{\text{num_countries} }\).
  • \(\psi\) معلمة في توزيع ذي الحدين السلبي لعدد من الوفيات.
  • \(\kappa\) هي المعلمة نطاق المشتركة للتوزيع HalfNormal على عدد التكاثر الأولي في كل بلد، \(\mu = \mu_1, ..., \mu_{\text{num_countries} }\) (تشير إلى أن عدد حالات إضافية تنتقل عن طريق كل شخص مصاب).
  • \(\alpha = \alpha_1, ..., \alpha_6\) هو فعالية كل من التدخلات ستة.
  • \(\epsilon\) (وتسمى ifr_noise في رمز، بعد كود ستان المؤلفين) هو الضوضاء في العدوى الوفيات معدل (IFR).

نعبر عن هذا النموذج باعتباره TFP JointDistribution ، وهو نوع من توزيع TFP يتيح التعبير عن النماذج الرسومية الاحتمالية.

def make_jd_prior(num_countries, num_interventions):
  return tfd.JointDistributionSequentialAutoBatched([
      # Rate parameter for the distribution of initial cases (tau).
      tfd.Exponential(rate=tf.cast(0.03, DTYPE)),

      # Initial cases for each country.
      lambda tau: tfd.Sample(
          tfd.Exponential(rate=tf.cast(1, DTYPE) / tau),
          sample_shape=num_countries),

      # Parameter in Negative Binomial model for deaths (psi).
      tfd.HalfNormal(scale=tf.cast(5, DTYPE)),

      # Parameter in the distribution over the initial reproduction number, R_0
      # (kappa).
      tfd.HalfNormal(scale=tf.cast(0.5, DTYPE)),

      # Initial reproduction number, R_0, for each country (mu).
      lambda kappa: tfd.Sample(
          tfd.TruncatedNormal(loc=3.28, scale=kappa, low=1e-5, high=1e5),
          sample_shape=num_countries),

      # Impact of interventions (alpha; shared for all countries).
      tfd.Sample(
          tfd.Gamma(tf.cast(0.1667, DTYPE), 1), sample_shape=num_interventions),

      # Multiplicative noise in Infection Fatality Rate.
      tfd.Sample(
          tfd.TruncatedNormal(
              loc=tf.cast(1., DTYPE), scale=0.1, low=1e-5, high=1e5),
              sample_shape=num_countries)
  ])

1.3 احتمالية الوفيات المرصودة مشروطة بقيم المعلمات

ويعبر عن نموذج احتمال \(p(\text{deaths} | \tau, y, \psi, \kappa, \mu, \alpha, \epsilon)\). يطبق النماذج الخاصة بعدد الإصابات والوفيات المتوقعة المشروطة بالمعلمات ، ويفترض أن الوفيات الفعلية تتبع التوزيع السلبي ذي الحدين.

def make_likelihood_fn(
    intervention_indicators, population, deaths,
    infection_fatality_rate, initial_days, total_days):

  # Create a mask for the initial days of simulated data, as they are not
  # counted in the likelihood.
  observed_deaths = tf.constant(deaths.T[np.newaxis, ...], dtype=DTYPE)
  mask_temp = deaths != -1
  mask_temp[:, :START_DAYS] = False
  observed_deaths_mask = tf.constant(mask_temp.T[np.newaxis, ...])

  conv_serial_interval = make_conv_serial_interval(initial_days, total_days)
  conv_fatality_rate = make_conv_fatality_rate(
      infection_fatality_rate, total_days)

  def likelihood_fn(tau, initial_cases, psi, kappa, mu, alpha_hier, ifr_noise):
    # Run models for infections and expected deaths
    predicted_infections = predict_infections(
        intervention_indicators, population, initial_cases, mu, alpha_hier,
        conv_serial_interval, initial_days, total_days)
    e_deaths_all_countries = predict_deaths(
        predicted_infections, ifr_noise, conv_fatality_rate)

    # Construct the Negative Binomial distribution for deaths by country.
    mu_m = tf.transpose(e_deaths_all_countries, [1, 0, 2])
    psi_m = psi[..., tf.newaxis, tf.newaxis]
    probs = tf.clip_by_value(mu_m / (mu_m + psi_m), 1e-9, 1.)
    likelihood_elementwise = tfd.NegativeBinomial(
        total_count=psi_m, probs=probs).log_prob(observed_deaths)
    return tf.reduce_sum(
        tf.where(observed_deaths_mask,
                likelihood_elementwise,
                tf.zeros_like(likelihood_elementwise)),
        axis=[-2, -1])

  return likelihood_fn

1.4 احتمال الوفاة نظرا للعدوى

يحسب هذا القسم توزيع الوفيات في الأيام التي تلي الإصابة. يفترض أن الوقت من الإصابة إلى الوفاة هو مجموع كميتين متفاوتتين جاما ، يمثلان الوقت من الإصابة إلى ظهور المرض والوقت من البداية إلى الوفاة. يتم الجمع بين توزيع الوقت للوصول الى الموت مع العدوى بيانات الوفيات تقييم من فيرتي وآخرون. (2020) لحساب احتمال الموت في أيام بعد الإصابة.

def daily_fatality_probability(infection_fatality_rate, total_days):
  """Computes the probability of death `d` days after infection."""

  # Convert from alternative Gamma parametrization and construct distributions
  # for number of days from infection to onset and onset to death.
  concentration1 = tf.cast((1. / 0.86)**2, DTYPE)
  rate1 = concentration1 / 5.1
  concentration2 = tf.cast((1. / 0.45)**2, DTYPE)
  rate2 = concentration2 / 18.8
  infection_to_onset = tfd.Gamma(concentration=concentration1, rate=rate1)
  onset_to_death = tfd.Gamma(concentration=concentration2, rate=rate2)

  # Create empirical distribution for number of days from infection to death.
  inf_to_death_dist = tfd.Empirical(
      infection_to_onset.sample([5e6]) + onset_to_death.sample([5e6]))

  # Subtract the CDF value at day i from the value at day i + 1 to compute the
  # probability of death on day i given infection on day 0, and given that
  # death (not recovery) is the outcome.
  times = np.arange(total_days + 1., dtype=DTYPE) + 0.5
  cdf = inf_to_death_dist.cdf(times).numpy()
  f_before_ifr = cdf[1:] - cdf[:-1]
  # Explicitly set the zeroth value to the empirical cdf at time 1.5, to include
  # the mass between time 0 and time .5.
  f_before_ifr[0] = cdf[1]

  # Multiply the daily fatality rates conditional on infection and eventual
  # death (f_before_ifr) by the infection fatality rates (probability of death
  # given intection) to obtain the probability of death on day i conditional
  # on infection on day 0.
  return infection_fatality_rate[..., np.newaxis] * f_before_ifr

def make_conv_fatality_rate(infection_fatality_rate, total_days):
  """Computes the probability of death on day `i` given infection on day `j`."""
  p_fatal_all_countries = daily_fatality_probability(
      infection_fatality_rate, total_days)

  # Use the probability of death d days after infection in each country
  # to build an array of shape [total_days - 1, total_days, num_countries],
  # where the element [i, j, c] is the probability of death on day i+1 given
  # infection on day j in country c.
  conv_fatality_rate = np.zeros(
      [total_days - 1, total_days, p_fatal_all_countries.shape[0]])
  for n in range(1, total_days):
    conv_fatality_rate[n - 1, 0:n, :] = (
        p_fatal_all_countries[:, n - 1::-1]).T
  return tf.constant(conv_fatality_rate, dtype=DTYPE)

1.5 الفاصل التسلسلي

الفاصل الزمني التسلسلي هو الوقت بين الحالات المتتالية في سلسلة انتقال المرض ، ويفترض أن يكون توزيع غاما. نحن نستخدم التوزيع الزمني المتسلسل لحساب احتمال أن الشخص المصاب في يوم \(i\) القبض على الفيروس من شخص مصاب سابقا في يوم \(j\) (و conv_serial_interval حجة ل predict_infections ).

def make_conv_serial_interval(initial_days, total_days):
  """Construct the convolutional kernel for infection timing."""

  g = tfd.Gamma(tf.cast(1. / (0.62**2), DTYPE), 1./(6.5*0.62**2))
  g_cdf = g.cdf(np.arange(total_days, dtype=DTYPE))

  # Approximate the probability mass function for the number of days between
  # successive infections.
  serial_interval = g_cdf[1:] - g_cdf[:-1]

  # `conv_serial_interval` is an array of shape
  # [total_days - initial_days, total_days] in which entry [i, j] contains the
  # probability that an individual infected on day i + initial_days caught the
  # virus from someone infected on day j.
  conv_serial_interval = np.zeros([total_days - initial_days, total_days])
  for n in range(initial_days, total_days):
    conv_serial_interval[n - initial_days, 0:n] = serial_interval[n - 1::-1]
  return tf.constant(conv_serial_interval, dtype=DTYPE)

2 المعالجة المسبقة للبيانات

COUNTRIES = [
    'Austria',
    'Belgium',
    'Denmark',
    'France',
    'Germany',
    'Italy',
    'Norway',
    'Spain',
    'Sweden',
    'Switzerland',
    'United_Kingdom'
]

2.1 بيانات تدخلات الجلب والمعالجة المسبقة

2.2 إحضار بيانات الحالة / الوفاة والانضمام إلى التدخلات

2.3 جلب ومعالجة نسبة الوفيات المصابة وبيانات السكان

2.4 المعالجة المسبقة للبيانات الخاصة بالبلد

# Model up to 75 days of data for each country, starting 30 days before the
# tenth cumulative death.
START_DAYS = 30
MAX_DAYS = 102
COVARIATE_COLUMNS = any_intervention_list + ['any_intervention']

# Initialize an array for number of deaths.
deaths = -np.ones((num_countries, MAX_DAYS), dtype=DTYPE)

# Assuming every intervention is still inplace in the unobserved future
num_interventions = len(COVARIATE_COLUMNS)
intervention_indicators = np.ones((num_countries, MAX_DAYS, num_interventions))

first_days = {}
for i, c in enumerate(COUNTRIES):
  c_data = data.loc[c]

  # Include data only after 10th death in a country.
  mask = c_data['deaths'].cumsum() >= 10

  # Get the date that the epidemic starts in a country.
  first_day = c_data.index[mask][0] - pd.to_timedelta(START_DAYS, 'days')
  c_data = c_data.truncate(before=first_day)

  # Truncate the data after 28 March 2020 for comparison with Flaxman et al.
  c_data = c_data.truncate(after='2020-03-28')

  c_data = c_data.iloc[:MAX_DAYS]
  days_of_data = c_data.shape[0]
  deaths[i, :days_of_data] = c_data['deaths']
  intervention_indicators[i, :days_of_data] = c_data[
    COVARIATE_COLUMNS].to_numpy()
  first_days[c] = first_day

# Number of sequential days to seed infections after the 10th death in a
# country. (N0 in authors' Stan code.)
INITIAL_DAYS = 6

# Number of days of observed data plus days to forecast. (N2 in authors' Stan
# code.)
TOTAL_DAYS = deaths.shape[1]

3 نموذج الاستدلال

Flaxman et al. (2020) المستخدمة ستان لعينة من الخلفية المعلمة مع هاملتون مونت كارلو (HMC) ولا-U-تشغيل عينات (المكسرات).

هنا ، نقوم بتطبيق HMC مع تكيف مزدوج متوسط ​​حجم الخطوة. نحن نستخدم تشغيلًا تجريبيًا لـ HMC للشروط المسبقة والتهيئة.

يعمل الاستنتاج في بضع دقائق على وحدة معالجة الرسومات.

3.1 بناء مسبق واحتمالية النموذج

jd_prior = make_jd_prior(num_countries, num_interventions)
likelihood_fn = make_likelihood_fn(
    intervention_indicators, population_value, deaths,
    infection_fatality_rate, INITIAL_DAYS, TOTAL_DAYS)

3.2 المرافق

def get_bijectors_from_samples(samples, unconstraining_bijectors, batch_axes):
  """Fit bijectors to the samples of a distribution.

  This fits a diagonal covariance multivariate Gaussian transformed by the
  `unconstraining_bijectors` to the provided samples. The resultant
  transformation can be used to precondition MCMC and other inference methods.
  """
  state_std = [    
      tf.math.reduce_std(bij.inverse(x), axis=batch_axes)
      for x, bij in zip(samples, unconstraining_bijectors)
  ]
  state_mu = [
      tf.math.reduce_mean(bij.inverse(x), axis=batch_axes)
      for x, bij in zip(samples, unconstraining_bijectors)
  ]
  return [tfb.Chain([cb, tfb.Shift(sh), tfb.Scale(sc)])
          for cb, sh, sc in zip(unconstraining_bijectors, state_mu, state_std)]

def generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors):
  """Creates an initial MCMC state, and bijectors from the prior."""
  prior_samples = jd_prior.sample(4096)

  bijectors = get_bijectors_from_samples(
      prior_samples, unconstraining_bijectors, batch_axes=0)

  init_state = [
    bij(tf.zeros([nchain] + list(s), DTYPE))
    for s, bij in zip(jd_prior.event_shape, bijectors)
  ]

  return init_state, bijectors

@tf.function(autograph=False, experimental_compile=True)
def sample_hmc(
    init_state,
    step_size,
    target_log_prob_fn,
    unconstraining_bijectors,
    num_steps=500,
    burnin=50,
    num_leapfrog_steps=10):

    def trace_fn(_, pkr):
        return {
            'target_log_prob': pkr.inner_results.inner_results.accepted_results.target_log_prob,
            'diverging': ~(pkr.inner_results.inner_results.log_accept_ratio > -1000.),
            'is_accepted': pkr.inner_results.inner_results.is_accepted,
            'step_size': [tf.exp(s) for s in pkr.log_averaging_step],
        }

    hmc = tfp.mcmc.HamiltonianMonteCarlo(
        target_log_prob_fn,
        step_size=step_size,
        num_leapfrog_steps=num_leapfrog_steps)

    hmc = tfp.mcmc.TransformedTransitionKernel(
        inner_kernel=hmc,
        bijector=unconstraining_bijectors)

    hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
        hmc,
        num_adaptation_steps=int(burnin * 0.8),
        target_accept_prob=0.8,
        decay_rate=0.5)

    # Sampling from the chain.
    return tfp.mcmc.sample_chain(
        num_results=burnin + num_steps,
        current_state=init_state,
        kernel=hmc,
        trace_fn=trace_fn)

3.3 تحديد أدوات قياس مساحة الحدث

مؤسسة حمد الطبية هي الأكثر فعالية عندما أخذ عينات من توزيع جاوس المتعدد الخواص ( Mangoubi وسميث (2017) )، وبالتالي فإن الخطوة الأولى هي شرط مسبق كثافة الهدف لنظرة قدر من هذا القبيل ممكن.

أولاً وقبل كل شيء ، نقوم بتحويل المتغيرات المقيدة (على سبيل المثال ، غير السلبية) إلى مساحة غير مقيدة ، والتي تتطلبها HMC. بالإضافة إلى ذلك ، نحن نستخدم bijector SinhArcsinh للتلاعب بثقل ذيول كثافة الهدف المحولة ؛ نحن نريد هذه لتسقط تقريبا كما \(e^{-x^2}\).

unconstraining_bijectors = [
    tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # tau
    tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # initial_cases
    tfb.Softplus(), # psi
    tfb.Softplus(), # kappa
    tfb.Softplus(), # mu
    tfb.Chain([tfb.Scale(tf.constant(0.4, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(skewness=tf.constant(-0.2, DTYPE), tailweight=tf.constant(2., DTYPE))]), # alpha
    tfb.Softplus(), # ifr_noise
]

3.4 التشغيل التجريبي لمؤسسة حمد الطبية

نقوم أولاً بتشغيل HMC بشرط مسبق من قبل ، مهيأ من 0 في الفضاء المحول. لا نستخدم العينات السابقة لتهيئة السلسلة كما هو الحال في الممارسة العملية التي تؤدي غالبًا إلى سلاسل متوقفة بسبب ضعف الأرقام.

%%time

nchain = 32

target_log_prob_fn = lambda *x: jd_prior.log_prob(*x) + likelihood_fn(*x)
init_state, bijectors = generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors)

# Each chain gets its own step size.
step_size = [tf.fill([nchain] + [1] * (len(s.shape) - 1), tf.constant(0.01, DTYPE)) for s in init_state]

burnin = 200
num_steps = 100

pilot_samples, pilot_sampler_stat = sample_hmc(
    init_state,
    step_size,
    target_log_prob_fn,
    bijectors,
    num_steps=num_steps,
    burnin=burnin,
    num_leapfrog_steps=10)

CPU times: user 56.8 s, sys: 2.34 s, total: 59.1 s
Wall time: 1min 1s

3.5 تصور العينات التجريبية

نحن نبحث عن سلاسل عالقة وتقارب مقلة العين. يمكننا إجراء تشخيص رسمي هنا ، لكن هذا ليس ضروريًا للغاية نظرًا لأنه مجرد تشغيل تجريبي.

import arviz as az
az.style.use('arviz-darkgrid')

var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']

pilot_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
                     for k, v in zip(var_name, pilot_samples)}

نلاحظ الاختلافات أثناء الإحماء ، ويرجع ذلك أساسًا إلى أن التكيف المزدوج لحجم الخطوة المتوسطة يستخدم بحثًا قويًا للغاية عن حجم الخطوة الأمثل. بمجرد إيقاف التكيف ، تختفي الاختلافات أيضًا.

az_trace = az.from_dict(posterior=pilot_with_warmup,
                        sample_stats={'diverging': np.swapaxes(pilot_sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));

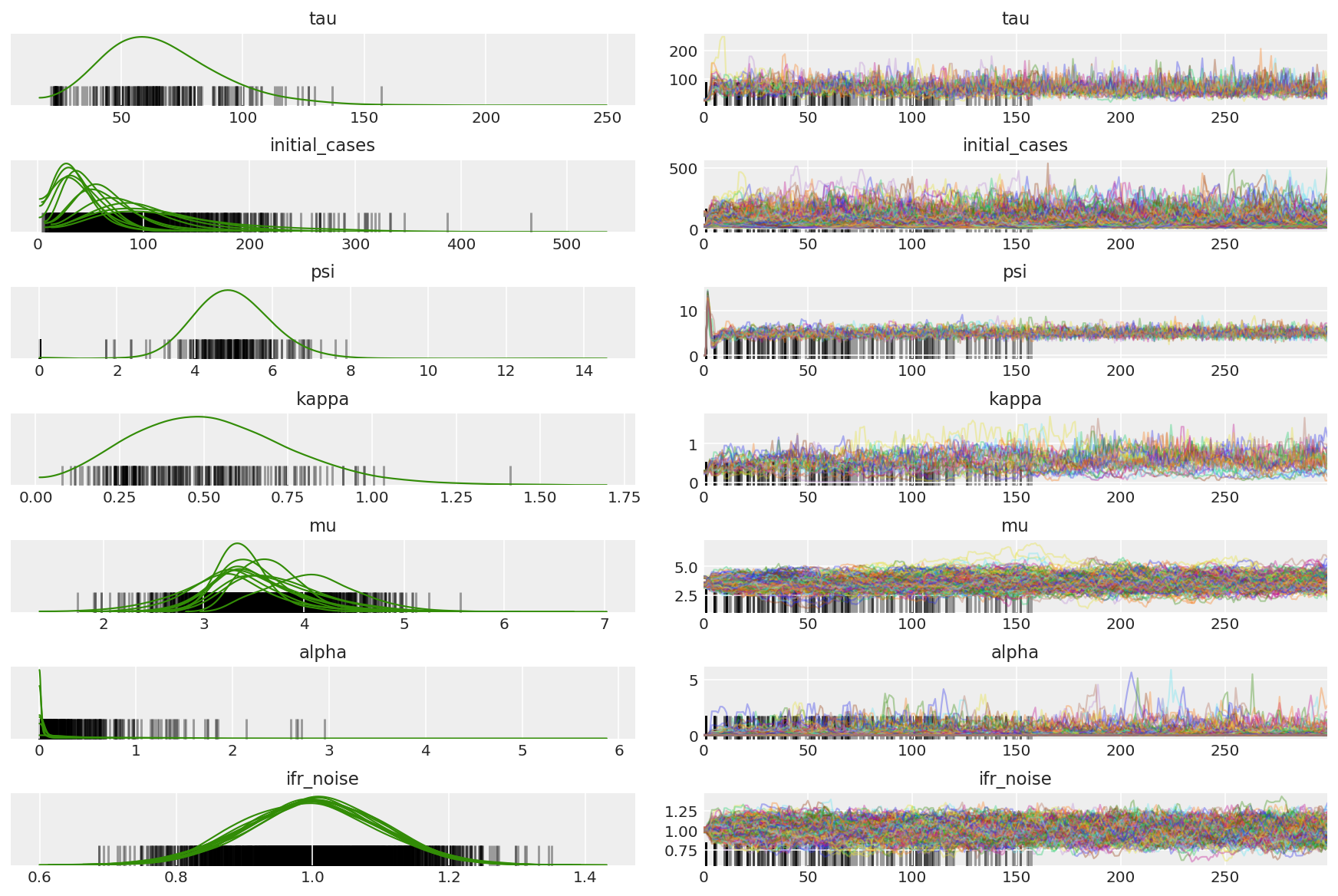
بي إن جي

plt.plot(pilot_sampler_stat['step_size'][0]);

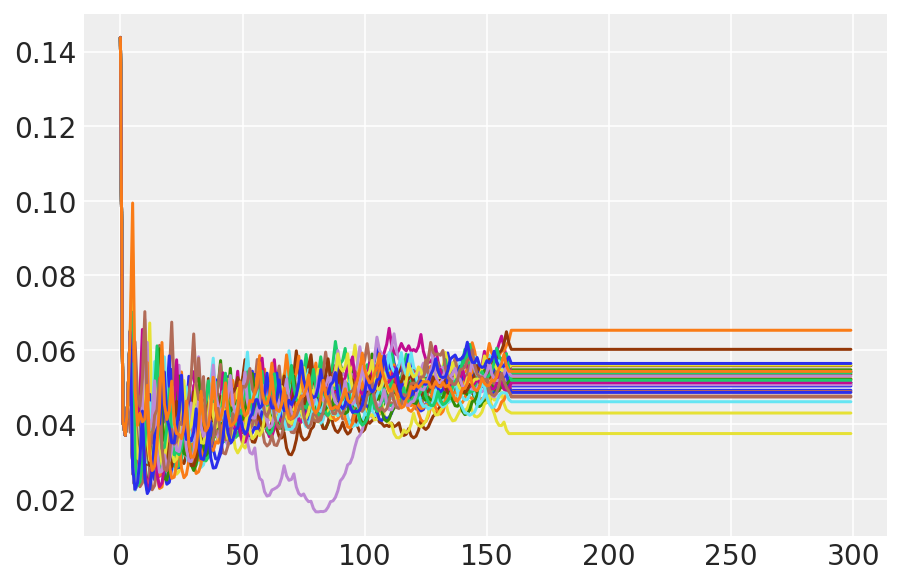
بي إن جي

3.6 قم بتشغيل HMC

من حيث المبدأ ، يمكننا استخدام العينات التجريبية للتحليل النهائي (إذا قمنا بتشغيلها لفترة أطول للحصول على تقارب) ، ولكن سيكون من الأكثر فاعلية بدء تشغيل HMC آخر ، هذه المرة مشروطة مسبقًا ومهيأة بواسطة عينات تجريبية.

%%time

burnin = 50
num_steps = 200

bijectors = get_bijectors_from_samples([s[burnin:] for s in pilot_samples],
                                       unconstraining_bijectors=unconstraining_bijectors,
                                       batch_axes=(0, 1))

samples, sampler_stat = sample_hmc(
    [s[-1] for s in pilot_samples],
    [s[-1] for s in pilot_sampler_stat['step_size']],
    target_log_prob_fn,
    bijectors,
    num_steps=num_steps,
    burnin=burnin,
    num_leapfrog_steps=20)

CPU times: user 1min 26s, sys: 3.88 s, total: 1min 30s
Wall time: 1min 32s

plt.plot(sampler_stat['step_size'][0]);

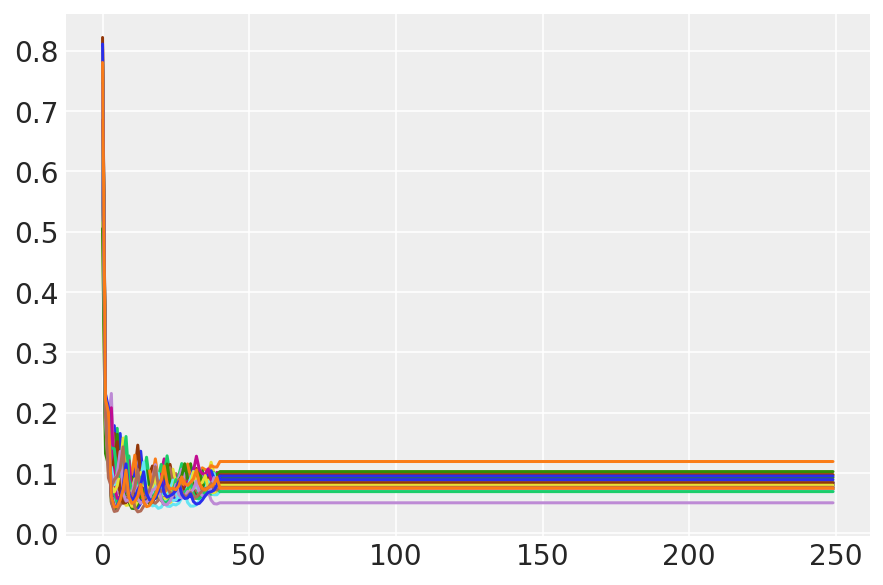
بي إن جي

3.7 تصور العينات

import arviz as az
az.style.use('arviz-darkgrid')

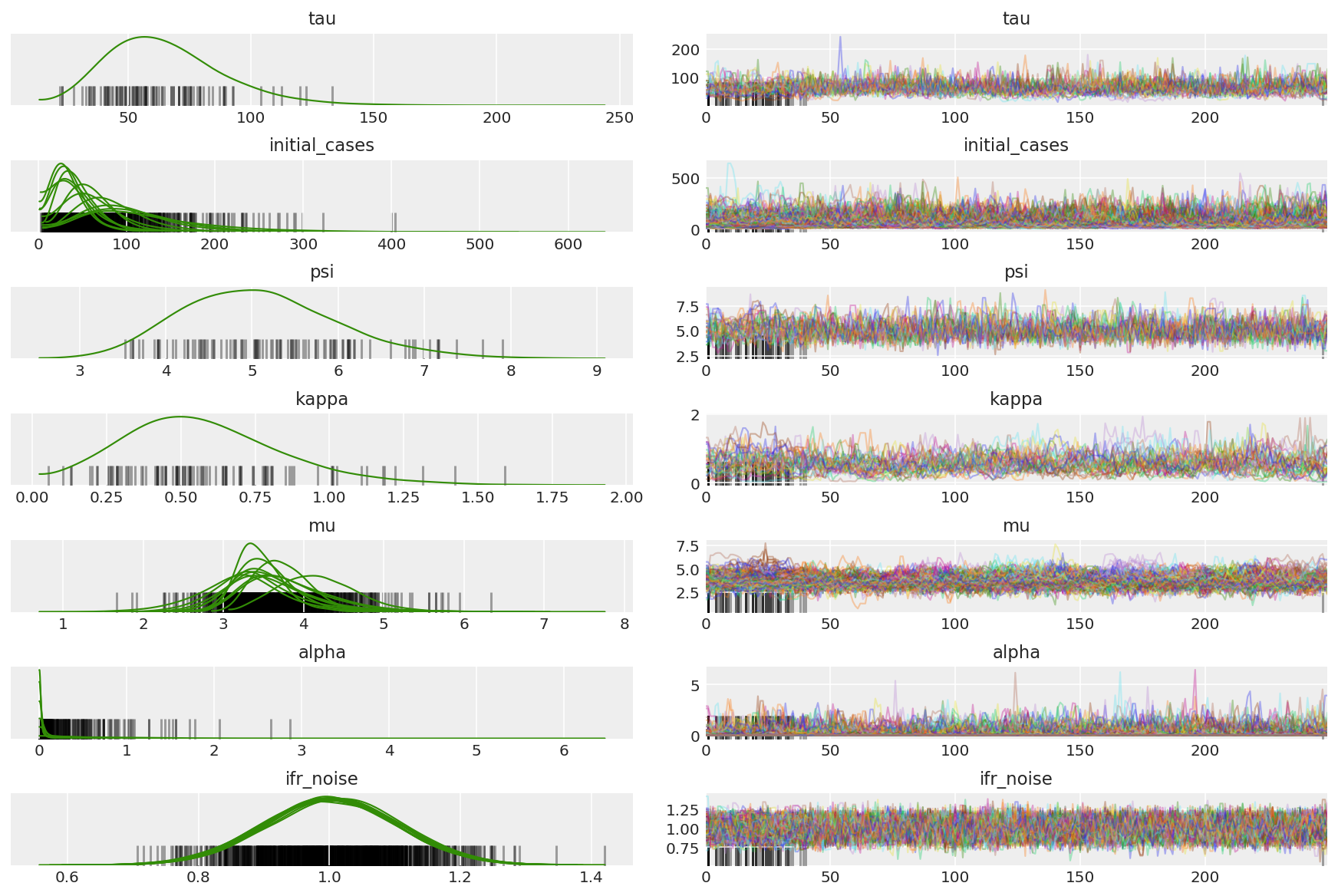
var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']

posterior = {k: np.swapaxes(v.numpy()[burnin:], 1, 0)
             for k, v in zip(var_name, samples)}
posterior_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
             for k, v in zip(var_name, samples)}

احسب ملخص السلاسل. نحن نبحث عن ESS عالي و r_hat قريب من 1.

az.summary(posterior)

az_trace = az.from_dict(posterior=posterior_with_warmup,
                        sample_stats={'diverging': np.swapaxes(sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));

بي إن جي

من المفيد إلقاء نظرة على وظائف الارتباط التلقائي عبر جميع الأبعاد. نحن نبحث عن وظائف تنخفض بسرعة ، ولكن ليس كثيرًا لدرجة أنها تدخل في الوضع السلبي (وهو ما يشير إلى أن HMC تصل إلى صدى ، وهو أمر سيء للقدرة على العمل ويمكن أن يؤدي إلى التحيز).

with az.rc_context(rc={'plot.max_subplots': None}):
  az.plot_autocorr(posterior, combined=True, figsize=(12, 16), textsize=12);

بي إن جي

4 نتائج

المؤامرات التالية تحليل التوزيعات التنبؤية الخلفية على \(R_t\)، عدد الوفيات، وعدد الإصابات، على غرار التحليل في فلاكسمان وآخرون. (2020).

total_num_samples = np.prod(posterior['mu'].shape[:2])

# Calculate R_t given parameter estimates.
def rt_samples_batched(mu, intervention_indicators, alpha):
  linear_prediction = tf.reduce_sum(
      intervention_indicators * alpha[..., np.newaxis, np.newaxis, :], axis=-1)
  rt_hat = mu[..., tf.newaxis] * tf.exp(-linear_prediction, name='rt')
  return rt_hat

alpha_hat = tf.convert_to_tensor(
    posterior['alpha'].reshape(total_num_samples, posterior['alpha'].shape[-1]))
mu_hat = tf.convert_to_tensor(
    posterior['mu'].reshape(total_num_samples, num_countries))
rt_hat = rt_samples_batched(mu_hat, intervention_indicators, alpha_hat)
sampled_initial_cases = posterior['initial_cases'].reshape(
    total_num_samples, num_countries)
sampled_ifr_noise = posterior['ifr_noise'].reshape(
    total_num_samples, num_countries)
psi_hat = posterior['psi'].reshape([total_num_samples])

conv_serial_interval = make_conv_serial_interval(INITIAL_DAYS, TOTAL_DAYS)
conv_fatality_rate = make_conv_fatality_rate(infection_fatality_rate, TOTAL_DAYS)
pred_hat = predict_infections(
    intervention_indicators, population_value, sampled_initial_cases, mu_hat,
    alpha_hat, conv_serial_interval, INITIAL_DAYS, TOTAL_DAYS)
expected_deaths = predict_deaths(pred_hat, sampled_ifr_noise, conv_fatality_rate)

psi_m = psi_hat[np.newaxis, ..., np.newaxis]
probs = tf.clip_by_value(expected_deaths / (expected_deaths + psi_m), 1e-9, 1.)
predicted_deaths = tfd.NegativeBinomial(
    total_count=psi_m, probs=probs).sample()

# Predict counterfactual infections/deaths in the absence of interventions
no_intervention_infections = predict_infections(
    intervention_indicators,
    population_value,
    sampled_initial_cases,
    mu_hat,
    tf.zeros_like(alpha_hat),
    conv_serial_interval,
    INITIAL_DAYS, TOTAL_DAYS)

no_intervention_expected_deaths = predict_deaths(
    no_intervention_infections, sampled_ifr_noise, conv_fatality_rate)
probs = tf.clip_by_value(
    no_intervention_expected_deaths / (no_intervention_expected_deaths + psi_m),
    1e-9, 1.)
no_intervention_predicted_deaths = tfd.NegativeBinomial(
    total_count=psi_m, probs=probs).sample()

4.1 فعالية التدخلات

على غرار الشكل 4 من Flaxman et al. (2020).

def intervention_effectiveness(alpha):

  alpha_adj = 1. - np.exp(-alpha + np.log(1.05) / 6.)
  alpha_adj_first = (
      1. - np.exp(-alpha - alpha[..., -1:] + np.log(1.05) / 6.))

  fig, ax = plt.subplots(1, 1, figsize=[12, 6])
  intervention_perm = [2, 1, 3, 4, 0]
  percentile_vals = [2.5, 97.5]
  jitter = .2

  for ind in range(5):
    first_low, first_high = tfp.stats.percentile(
        alpha_adj_first[..., ind], percentile_vals)
    low, high = tfp.stats.percentile(
        alpha_adj[..., ind], percentile_vals)

    p_ind = intervention_perm[ind]
    ax.hlines(p_ind, low, high, label='Later Intervention', colors='g')
    ax.scatter(alpha_adj[..., ind].mean(), p_ind, color='g')
    ax.hlines(p_ind + jitter, first_low, first_high,
              label='First Intervention', colors='r')
    ax.scatter(alpha_adj_first[..., ind].mean(), p_ind + jitter, color='r')

    if ind == 0:
      plt.legend(loc='lower right')
  ax.set_yticks(range(5))
  ax.set_yticklabels(
      [any_intervention_list[intervention_perm.index(p)] for p in range(5)])
  ax.set_xlim([-0.01, 1.])
  r = fig.patch
  r.set_facecolor('white') 

intervention_effectiveness(alpha_hat)

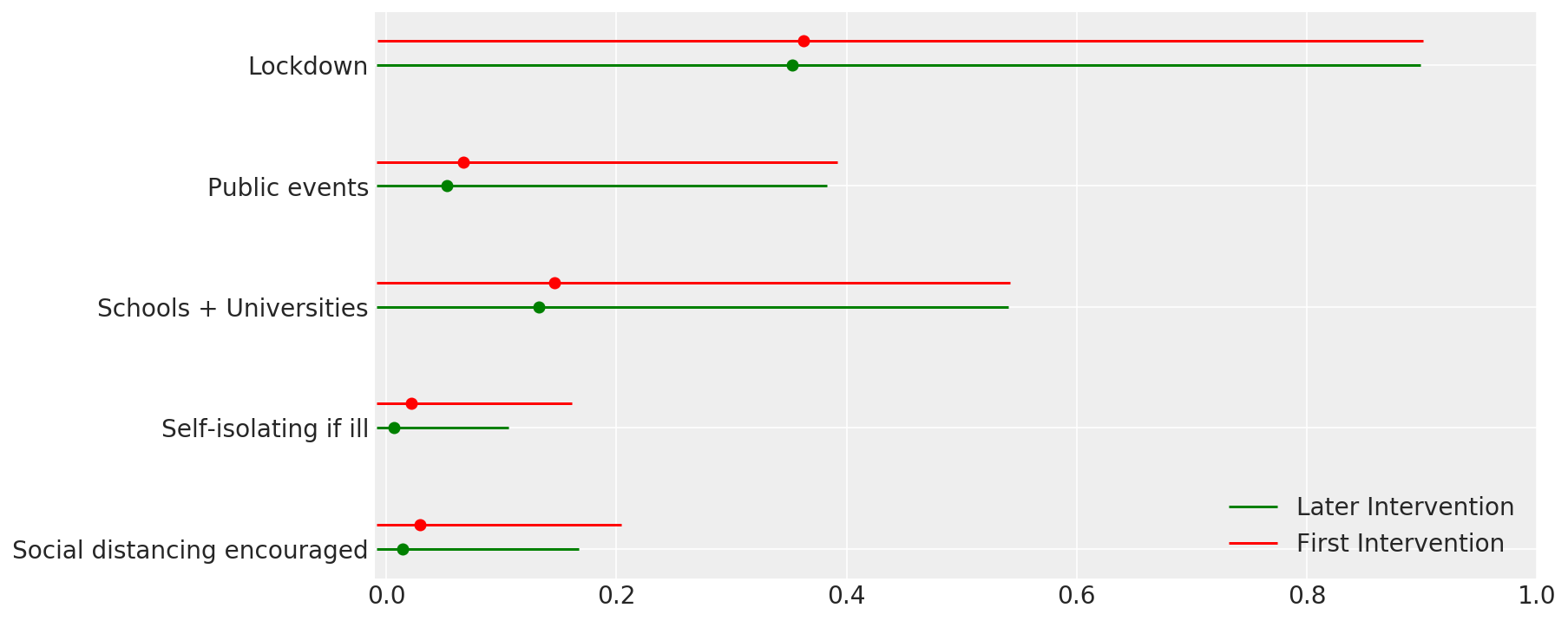
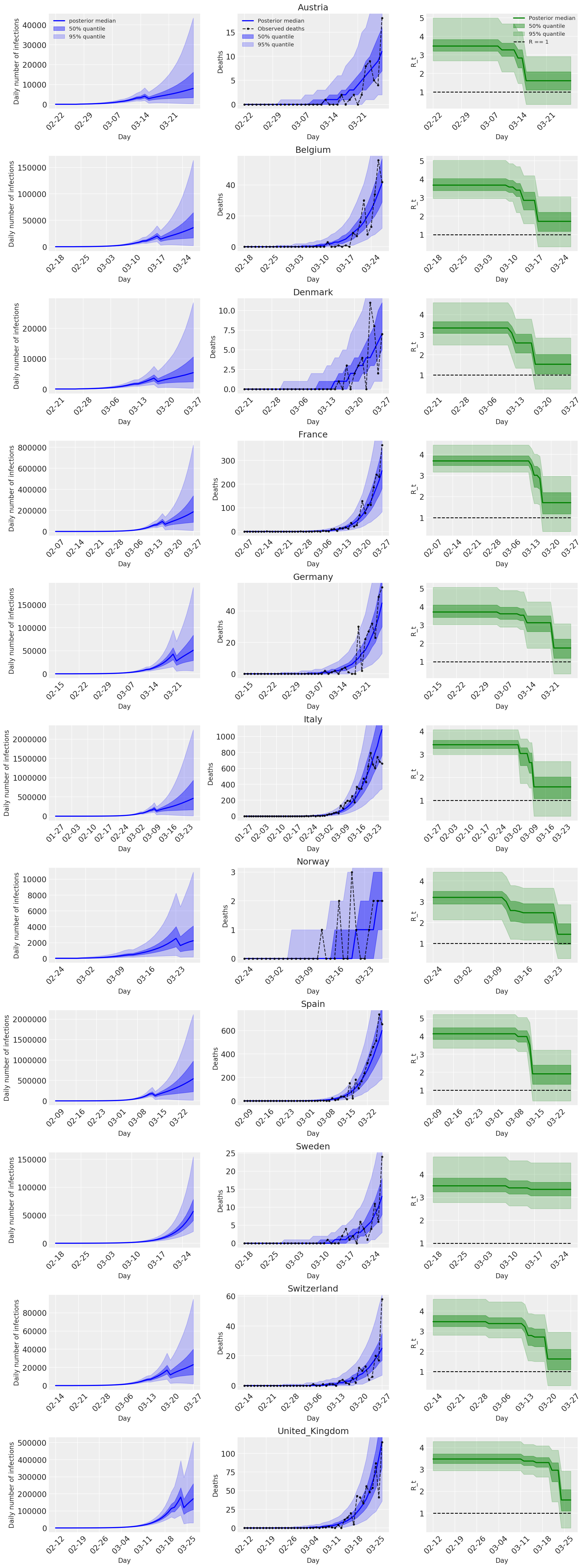
بي إن جي

4.2 العدوى والوفيات و R_t حسب البلد

على غرار الشكل 2 من Flaxman et al. (2020).

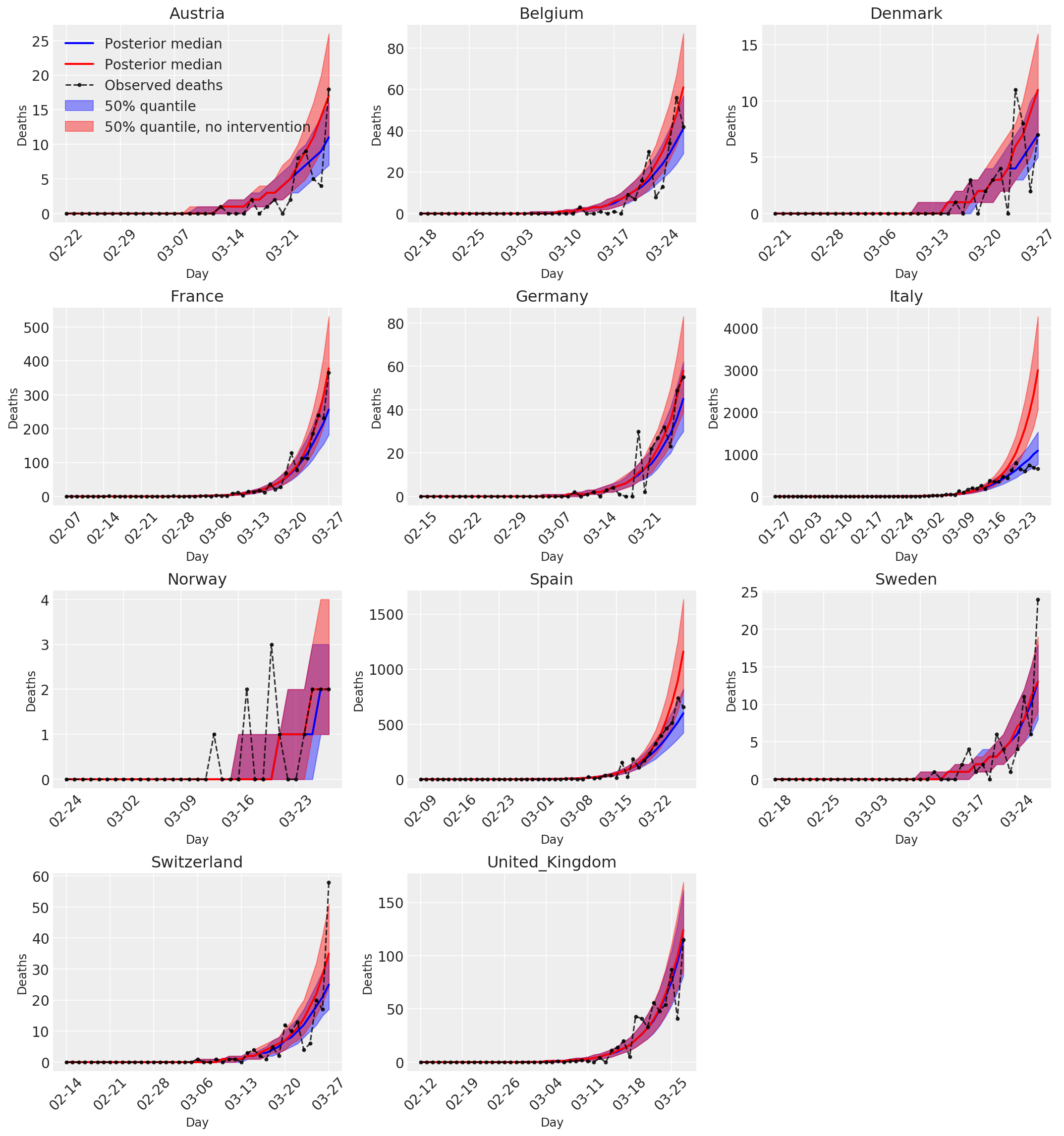
بي إن جي

4.3 العدد اليومي للوفيات المتوقعة / المتوقعة مع التدخلات وبدونها

بي إن جي