 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Problem osiem szkół ( Rubin 1981 ) uważa, że skuteczność programów coachingowych SAT prowadzonych równolegle w ośmiu szkołach. Stało się klasyczny problem ( Bayesa Analiza danych , Stan ), który ilustruje przydatność modelowania hierarchicznego do wymiany informacji między grupami wymiennymi.
Poniższa implementacja jest adaptacją Edward 1,0 tutorialu .
Import
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
import warnings
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
Dane
Z Bayesowskiej analizy danych, rozdział 5.5 (Gelman et al. 2013):
Przeprowadzono badanie dla Educational Testing Service w celu przeanalizowania efektów specjalnych programów coachingowych dla SAT-V (Scholastic Aptitude Test-Verbal) w każdej z ośmiu szkół średnich. Zmienną wyniku w każdym badaniu był wynik specjalnego wykonania testu SAT-V, standaryzowanego testu wielokrotnego wyboru administrowanego przez Educational Testing Service i wykorzystywanego do pomocy uczelniom w podejmowaniu decyzji o przyjęciu; wyniki mogą wahać się od 200 do 800, ze średnią około 500 i odchyleniem standardowym około 100. Egzaminy SAT są zaprojektowane tak, aby były odporne na krótkoterminowe wysiłki ukierunkowane na poprawę wyników na teście; zamiast tego są zaprojektowane tak, aby odzwierciedlały zdobytą wiedzę i umiejętności wypracowane przez wiele lat edukacji. Niemniej jednak każda z ośmiu szkół w tym badaniu uznała, że jej krótkoterminowy program coachingowy jest bardzo skuteczny w zwiększaniu wyników SAT. Ponadto nie było wcześniej powodu, by sądzić, że którykolwiek z ośmiu programów był bardziej skuteczny niż jakikolwiek inny lub że niektóre z nich były bardziej do siebie podobne niż do innych.
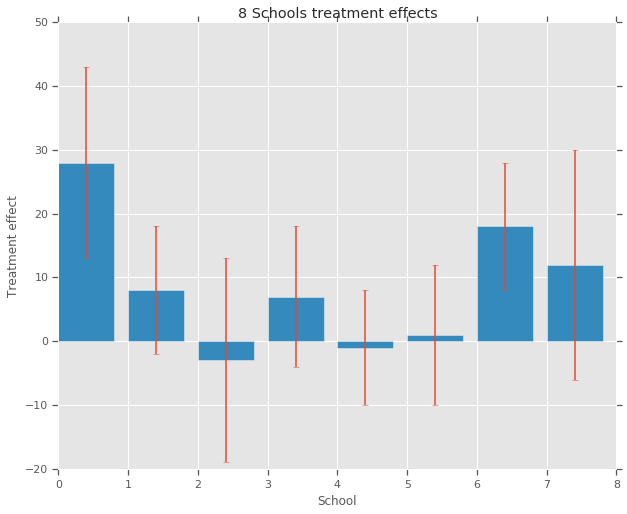
Dla każdego z ośmiu szkół (\(J = 8\)), mamy szacowany efekt leczenia \(y_j\) i błąd standardowy efekt kosztorysowej \(\sigma_j\). Efekty leczenia w badaniu uzyskano przez regresję liniową w grupie leczonej przy użyciu wyników PSAT-M i PSAT-V jako zmiennych kontrolnych. Ponieważ nie było przed przekonanie, że każda ze szkół były mniej lub bardziej podobny albo że którykolwiek z programów coachingowych byłaby bardziej efektywna, możemy rozważyć skutki zabiegów jak wymienny .
num_schools = 8 # number of schools
treatment_effects = np.array(
[28, 8, -3, 7, -1, 1, 18, 12], dtype=np.float32) # treatment effects
treatment_stddevs = np.array(
[15, 10, 16, 11, 9, 11, 10, 18], dtype=np.float32) # treatment SE
fig, ax = plt.subplots()
plt.bar(range(num_schools), treatment_effects, yerr=treatment_stddevs)
plt.title("8 Schools treatment effects")
plt.xlabel("School")
plt.ylabel("Treatment effect")
fig.set_size_inches(10, 8)
plt.show()
Model
Do przechwytywania danych używamy hierarchicznego modelu normalnego. Podąża za procesem generatywnym,
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i \sim \text{Normal}\left(\text{loc}{=}\mu,\ \text{scale}{=}\tau \right) \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
gdzie \(\mu\) reprezentuje wcześniejsze średnią skuteczność leczenia i \(\tau\) kontrole ile istnieje rozbieżność między szkołami. \(y_i\) i \(\sigma_i\) są przestrzegane. Jako \(\tau \rightarrow \infty\)model zbliża się do modelu no-pooling, czyli każda z szacunkami efekt leczenia szkole mogą być bardziej niezależne. Jako \(\tau \rightarrow 0\)model zbliża się do modelu complete-poolingu, tj wszystkich efektów leczenia szkoły są bliżej do grupy średniej \(\mu\). W celu ograniczenia odchylenia standardowego jest pozytywny, zwracamy \(\tau\) z rozkładu logarytmiczno-normalnego (co jest równoważne rysunku \(log(\tau)\) z normalnym rozkładem).
W następstwie Diagnozowanie Stronnicze Wnioskowanie z rozbieżności , możemy przekształcić model powyższe pod równoważną non-centered modelu:
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i' \sim \text{Normal}\left(\text{loc}{=}0,\ \text{scale}{=}1 \right) \\ & \theta_i = \mu + \tau \theta_i' \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
Mamy zreifikować ten model jako JointDistributionSequential przykład:
model = tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=10., name="avg_effect"), # `mu` above
tfd.Normal(loc=5., scale=1., name="avg_stddev"), # `log(tau)` above
tfd.Independent(tfd.Normal(loc=tf.zeros(num_schools),
scale=tf.ones(num_schools),
name="school_effects_standard"), # `theta_prime`
reinterpreted_batch_ndims=1),
lambda school_effects_standard, avg_stddev, avg_effect: (
tfd.Independent(tfd.Normal(loc=(avg_effect[..., tf.newaxis] +
tf.exp(avg_stddev[..., tf.newaxis]) *
school_effects_standard), # `theta` above
scale=treatment_stddevs),
name="treatment_effects", # `y` above
reinterpreted_batch_ndims=1))
])
def target_log_prob_fn(avg_effect, avg_stddev, school_effects_standard):
"""Unnormalized target density as a function of states."""
return model.log_prob((
avg_effect, avg_stddev, school_effects_standard, treatment_effects))
Wnioskowanie bayesowskie
Na podstawie danych wykonujemy hamiltonian Monte Carlo (HMC), aby obliczyć rozkład a posteriori nad parametrami modelu.
num_results = 5000
num_burnin_steps = 3000
# Improve performance by tracing the sampler using `tf.function`
# and compiling it using XLA.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
tf.zeros([], name='init_avg_effect'),
tf.zeros([], name='init_avg_stddev'),
tf.ones([num_schools], name='init_school_effects_standard'),
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.4,
num_leapfrog_steps=3))
states, kernel_results = do_sampling()
avg_effect, avg_stddev, school_effects_standard = states
school_effects_samples = (
avg_effect[:, np.newaxis] +
np.exp(avg_stddev)[:, np.newaxis] * school_effects_standard)
num_accepted = np.sum(kernel_results.is_accepted)
print('Acceptance rate: {}'.format(num_accepted / num_results))
Acceptance rate: 0.5974
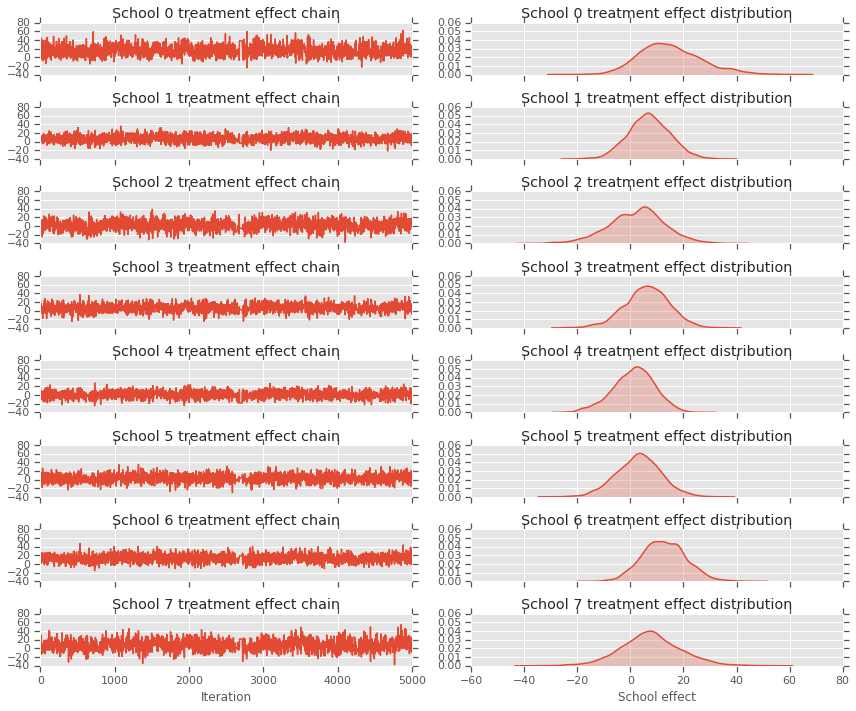
fig, axes = plt.subplots(8, 2, sharex='col', sharey='col')
fig.set_size_inches(12, 10)
for i in range(num_schools):
axes[i][0].plot(school_effects_samples[:,i].numpy())
axes[i][0].title.set_text("School {} treatment effect chain".format(i))
sns.kdeplot(school_effects_samples[:,i].numpy(), ax=axes[i][1], shade=True)
axes[i][1].title.set_text("School {} treatment effect distribution".format(i))
axes[num_schools - 1][0].set_xlabel("Iteration")
axes[num_schools - 1][1].set_xlabel("School effect")
fig.tight_layout()
plt.show()
print("E[avg_effect] = {}".format(np.mean(avg_effect)))
print("E[avg_stddev] = {}".format(np.mean(avg_stddev)))
print("E[school_effects_standard] =")
print(np.mean(school_effects_standard[:, ]))
print("E[school_effects] =")
print(np.mean(school_effects_samples[:, ], axis=0))
E[avg_effect] = 5.57183933258 E[avg_stddev] = 2.47738981247 E[school_effects_standard] = 0.08509017 E[school_effects] = [15.0051 7.103311 2.4552586 6.2744603 1.3364682 3.1125953 12.762501 7.743602 ]
# Compute the 95% interval for school_effects
school_effects_low = np.array([
np.percentile(school_effects_samples[:, i], 2.5) for i in range(num_schools)
])
school_effects_med = np.array([
np.percentile(school_effects_samples[:, i], 50) for i in range(num_schools)
])
school_effects_hi = np.array([
np.percentile(school_effects_samples[:, i], 97.5)
for i in range(num_schools)
])
fig, ax = plt.subplots(nrows=1, ncols=1, sharex=True)
ax.scatter(np.array(range(num_schools)), school_effects_med, color='red', s=60)
ax.scatter(
np.array(range(num_schools)) + 0.1, treatment_effects, color='blue', s=60)
plt.plot([-0.2, 7.4], [np.mean(avg_effect),
np.mean(avg_effect)], 'k', linestyle='--')
ax.errorbar(
np.array(range(8)),
school_effects_med,
yerr=[
school_effects_med - school_effects_low,
school_effects_hi - school_effects_med
],
fmt='none')
ax.legend(('avg_effect', 'HMC', 'Observed effect'), fontsize=14)
plt.xlabel('School')
plt.ylabel('Treatment effect')
plt.title('HMC estimated school treatment effects vs. observed data')
fig.set_size_inches(10, 8)
plt.show()
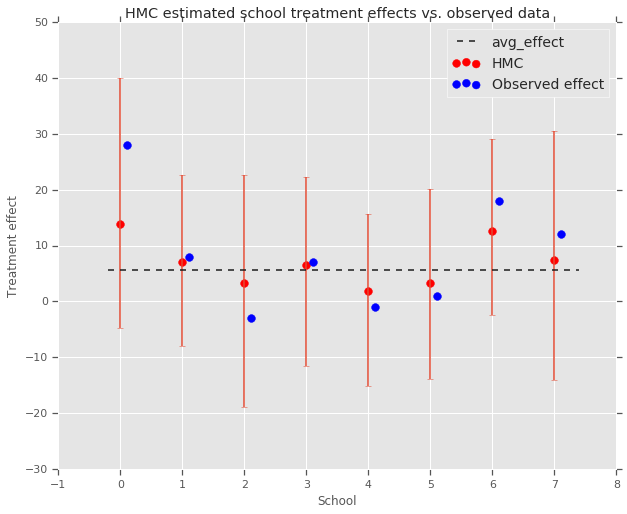
Możemy zaobserwować skurcz w kierunku grupy avg_effect powyżej.
print("Inferred posterior mean: {0:.2f}".format(
np.mean(school_effects_samples[:,])))
print("Inferred posterior mean se: {0:.2f}".format(
np.std(school_effects_samples[:,])))
Inferred posterior mean: 6.97 Inferred posterior mean se: 10.41
Krytyka
Aby uzyskać tylną dystrybucję predykcyjną, czyli nowy model danych \(y^*\) daną obserwowanych danych \(y\):
\[ p(y^*|y) \propto \int_\theta p(y^* | \theta)p(\theta |y)d\theta\]
możemy zastąpić wartości zmiennych losowych w modelu, aby ustawić je na średnią rozkładu a posteriori, a próbki z tego modelu, aby wygenerować nowe dane \(y^*\).
sample_shape = [5000]
_, _, _, predictive_treatment_effects = model.sample(
value=(tf.broadcast_to(np.mean(avg_effect, 0), sample_shape),
tf.broadcast_to(np.mean(avg_stddev, 0), sample_shape),
tf.broadcast_to(np.mean(school_effects_standard, 0),
sample_shape + [num_schools]),
None))
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(predictive_treatment_effects[:, 2*i].numpy(),
ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect posterior predictive".format(2*i))
sns.kdeplot(predictive_treatment_effects[:, 2*i + 1].numpy(),
ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect posterior predictive".format(2*i + 1))
plt.show()
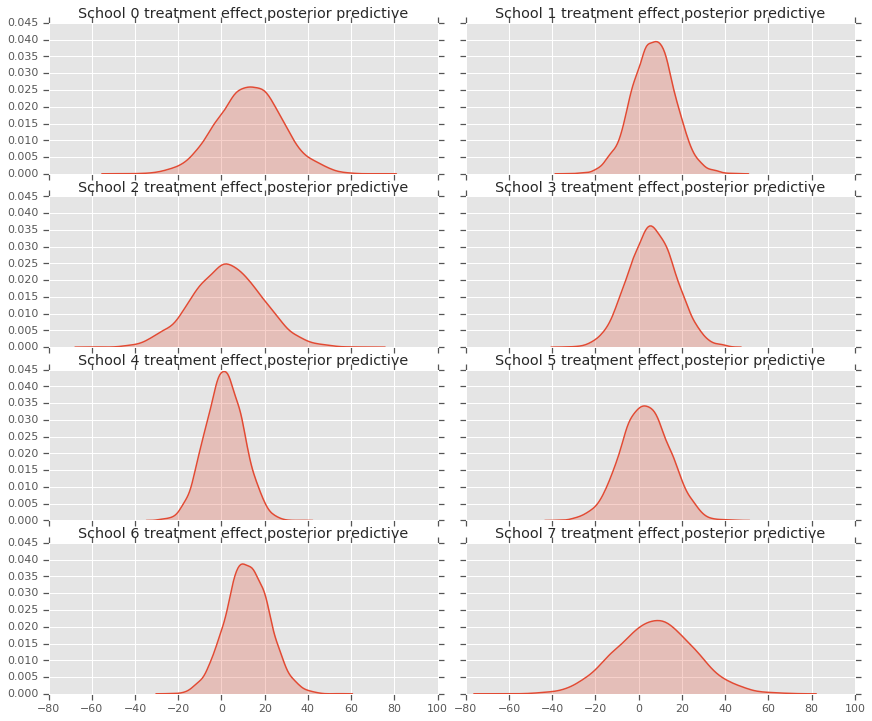
# The mean predicted treatment effects for each of the eight schools.
prediction = np.mean(predictive_treatment_effects, axis=0)
Możemy spojrzeć na reszty między danymi dotyczącymi efektów leczenia a przewidywaniami modelu a posteriori. Odpowiadają one powyższemu wykresowi, który pokazuje kurczenie się szacowanych efektów w stosunku do średniej populacji.
treatment_effects - prediction
array([14.905351 , 1.2838383, -5.6966295, 0.8327627, -2.3356671,
-2.0363257, 5.997898 , 4.3731265], dtype=float32)
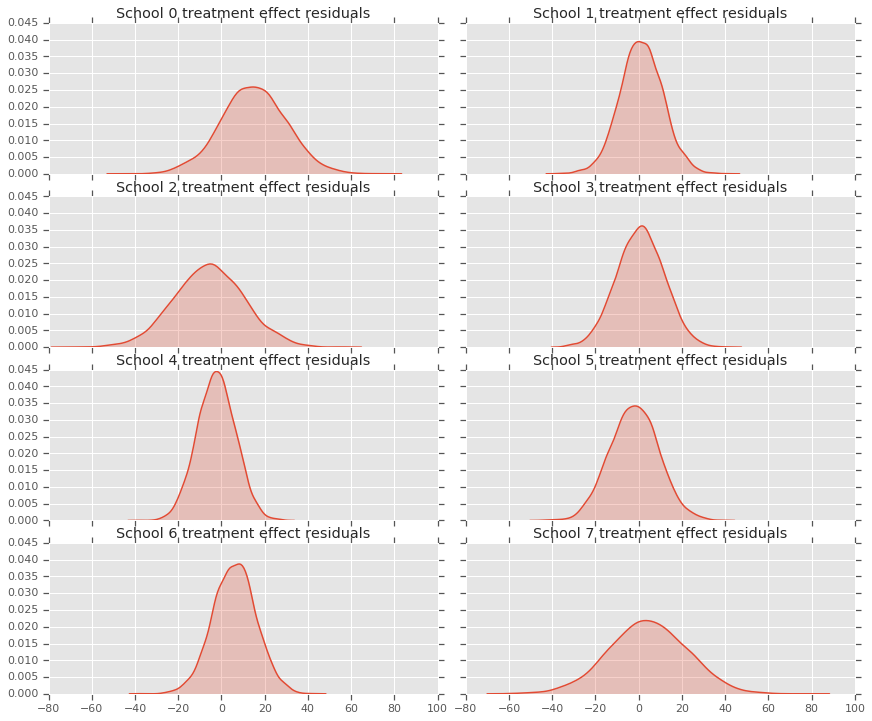
Ponieważ mamy rozkład prognoz dla każdej szkoły, możemy również rozważyć rozkład reszt.
residuals = treatment_effects - predictive_treatment_effects
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(residuals[:, 2*i].numpy(), ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect residuals".format(2*i))
sns.kdeplot(residuals[:, 2*i + 1].numpy(), ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect residuals".format(2*i + 1))
plt.show()
Podziękowanie
W Edward 1.0 (Ten poradnik został napisany źródłowego ). Dziękujemy wszystkim współtwórcom za napisanie i poprawienie tej wersji.
Bibliografia
- Donalda B. Rubina. Estymacja w równoległych eksperymentach randomizowanych. Journal of Educational Statistics, 6(4):377-401, 1981.
- Andrew Gelman, John Carlin, Hal Stern, David Dunson, Aki Vehtari i Donald Rubin. Bayesowska analiza danych, wydanie trzecie. Chapman i Hall/CRC, 2013.
