 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza la fonte su GitHub Visualizza la fonte su GitHub |  Scarica taccuino Scarica taccuino |
Il problema otto scuole ( Rubin 1981 ) considera l'efficacia dei programmi di coaching SAT condotti in parallelo in otto scuole. E 'diventato un classico problema ( bayesiana analisi dei dati , Stan ) che illustra l'utilità di modellazione gerarchica per la condivisione delle informazioni tra i gruppi intercambiabili.
Il L'implementazione segue è un adattamento di un Edward 1,0 esercitazione .
Importazioni
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
import warnings
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
I dati
Dall'analisi dei dati bayesiani, sezione 5.5 (Gelman et al. 2013):
Per conto del Servizio Prove Educative è stato condotto uno studio per analizzare gli effetti di speciali programmi di coaching per SAT-V (Scholastic Attitude Test-Verbal) in ciascuna delle otto scuole superiori. La variabile di esito in ogni studio era il punteggio su un'amministrazione speciale del SAT-V, un test a scelta multipla standardizzato somministrato dall'Educational Testing Service e utilizzato per aiutare i college a prendere decisioni di ammissione; i punteggi possono variare tra 200 e 800, con media circa 500 e deviazione standard circa 100. Gli esami SAT sono progettati per resistere a sforzi a breve termine diretti specificamente al miglioramento delle prestazioni del test; invece sono progettati per riflettere le conoscenze acquisite e le abilità sviluppate in molti anni di istruzione. Tuttavia, ciascuna delle otto scuole in questo studio ha considerato il suo programma di coaching a breve termine molto efficace nell'aumentare i punteggi SAT. Inoltre, non vi era alcuna ragione preliminare per ritenere che uno degli otto programmi fosse più efficace di un altro o che alcuni fossero più simili negli effetti l'uno all'altro che a qualsiasi altro.
Per ciascuno degli otto scuole (\(J = 8\)), abbiamo un effetto del trattamento stimato \(y_j\) e un errore standard di stima dell'effetto \(\sigma_j\). Gli effetti del trattamento nello studio sono stati ottenuti mediante una regressione lineare sul gruppo di trattamento utilizzando i punteggi PSAT-M e PSAT-V come variabili di controllo. Poiché non vi era alcuna convinzione prima che una qualsiasi delle scuole erano più o meno simili, o che uno dei programmi di coaching sarebbe più efficace, possiamo considerare gli effetti del trattamento come intercambiabile .
num_schools = 8 # number of schools
treatment_effects = np.array(
[28, 8, -3, 7, -1, 1, 18, 12], dtype=np.float32) # treatment effects
treatment_stddevs = np.array(
[15, 10, 16, 11, 9, 11, 10, 18], dtype=np.float32) # treatment SE
fig, ax = plt.subplots()
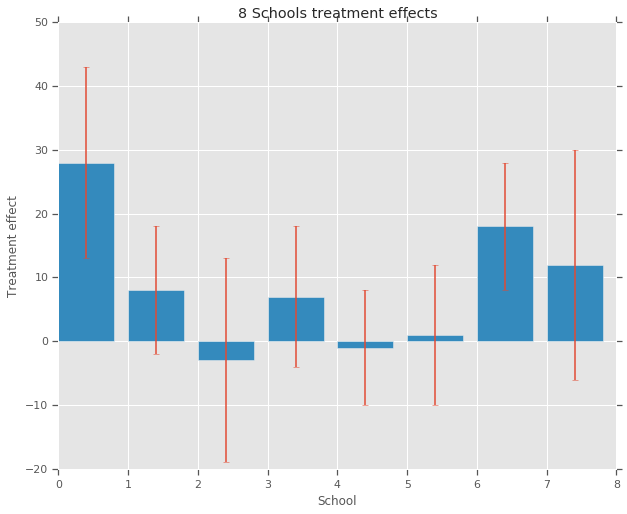
plt.bar(range(num_schools), treatment_effects, yerr=treatment_stddevs)
plt.title("8 Schools treatment effects")
plt.xlabel("School")
plt.ylabel("Treatment effect")
fig.set_size_inches(10, 8)
plt.show()
Modello
Per acquisire i dati, utilizziamo un modello normale gerarchico. Segue il processo generativo,
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i \sim \text{Normal}\left(\text{loc}{=}\mu,\ \text{scale}{=}\tau \right) \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
dove \(\mu\) rappresenta l'effetto medio di trattamento e di quelli precedenti \(\tau\) controlla quanto varianza c'è tra scuole. Il \(y_i\) e \(\sigma_i\) sono osservate. Come \(\tau \rightarrow \infty\), il modello si avvicina il modello no-pooling, vale a dire, ciascuna delle stime dell'effetto del trattamento della scuola sono autorizzati a essere più indipendente. Come \(\tau \rightarrow 0\), il modello si avvicina al modello completo-pooling, vale a dire, tutti gli effetti del trattamento della scuola sono più vicini al gruppo media \(\mu\). Per limitare la deviazione standard è positivo, tracciamo \(\tau\) da una distribuzione lognormale (che equivale al disegno \(log(\tau)\) da una distribuzione normale).
A seguito di Diagnosi Biased Inference con divergenze , trasformiamo il modello di cui sopra in un modello non centrato equivalente:
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i' \sim \text{Normal}\left(\text{loc}{=}0,\ \text{scale}{=}1 \right) \\ & \theta_i = \mu + \tau \theta_i' \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
Abbiamo reificare questo modello come JointDistributionSequential esempio:
model = tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=10., name="avg_effect"), # `mu` above
tfd.Normal(loc=5., scale=1., name="avg_stddev"), # `log(tau)` above
tfd.Independent(tfd.Normal(loc=tf.zeros(num_schools),
scale=tf.ones(num_schools),
name="school_effects_standard"), # `theta_prime`
reinterpreted_batch_ndims=1),
lambda school_effects_standard, avg_stddev, avg_effect: (
tfd.Independent(tfd.Normal(loc=(avg_effect[..., tf.newaxis] +
tf.exp(avg_stddev[..., tf.newaxis]) *
school_effects_standard), # `theta` above
scale=treatment_stddevs),
name="treatment_effects", # `y` above
reinterpreted_batch_ndims=1))
])
def target_log_prob_fn(avg_effect, avg_stddev, school_effects_standard):
"""Unnormalized target density as a function of states."""
return model.log_prob((
avg_effect, avg_stddev, school_effects_standard, treatment_effects))
Inferenza bayesiana
Dati i dati, eseguiamo Hamiltonian Monte Carlo (HMC) per calcolare la distribuzione a posteriori sui parametri del modello.
num_results = 5000
num_burnin_steps = 3000
# Improve performance by tracing the sampler using `tf.function`
# and compiling it using XLA.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
tf.zeros([], name='init_avg_effect'),
tf.zeros([], name='init_avg_stddev'),
tf.ones([num_schools], name='init_school_effects_standard'),
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.4,
num_leapfrog_steps=3))
states, kernel_results = do_sampling()
avg_effect, avg_stddev, school_effects_standard = states
school_effects_samples = (
avg_effect[:, np.newaxis] +
np.exp(avg_stddev)[:, np.newaxis] * school_effects_standard)
num_accepted = np.sum(kernel_results.is_accepted)
print('Acceptance rate: {}'.format(num_accepted / num_results))
Acceptance rate: 0.5974
fig, axes = plt.subplots(8, 2, sharex='col', sharey='col')
fig.set_size_inches(12, 10)
for i in range(num_schools):
axes[i][0].plot(school_effects_samples[:,i].numpy())
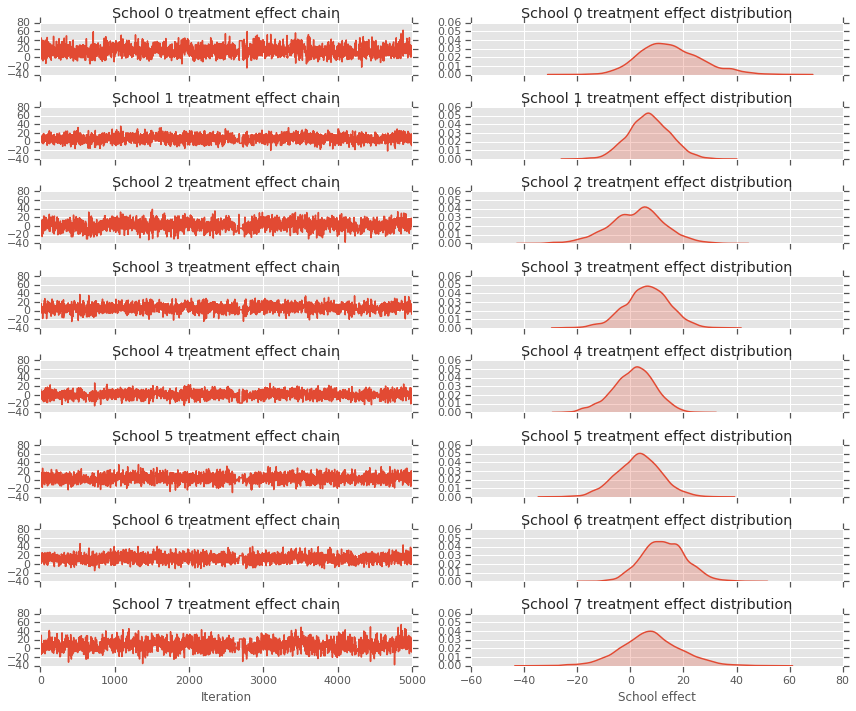
axes[i][0].title.set_text("School {} treatment effect chain".format(i))
sns.kdeplot(school_effects_samples[:,i].numpy(), ax=axes[i][1], shade=True)
axes[i][1].title.set_text("School {} treatment effect distribution".format(i))
axes[num_schools - 1][0].set_xlabel("Iteration")
axes[num_schools - 1][1].set_xlabel("School effect")
fig.tight_layout()
plt.show()
print("E[avg_effect] = {}".format(np.mean(avg_effect)))
print("E[avg_stddev] = {}".format(np.mean(avg_stddev)))
print("E[school_effects_standard] =")
print(np.mean(school_effects_standard[:, ]))
print("E[school_effects] =")
print(np.mean(school_effects_samples[:, ], axis=0))
E[avg_effect] = 5.57183933258 E[avg_stddev] = 2.47738981247 E[school_effects_standard] = 0.08509017 E[school_effects] = [15.0051 7.103311 2.4552586 6.2744603 1.3364682 3.1125953 12.762501 7.743602 ]
# Compute the 95% interval for school_effects
school_effects_low = np.array([
np.percentile(school_effects_samples[:, i], 2.5) for i in range(num_schools)
])
school_effects_med = np.array([
np.percentile(school_effects_samples[:, i], 50) for i in range(num_schools)
])
school_effects_hi = np.array([
np.percentile(school_effects_samples[:, i], 97.5)
for i in range(num_schools)
])
fig, ax = plt.subplots(nrows=1, ncols=1, sharex=True)
ax.scatter(np.array(range(num_schools)), school_effects_med, color='red', s=60)
ax.scatter(
np.array(range(num_schools)) + 0.1, treatment_effects, color='blue', s=60)
plt.plot([-0.2, 7.4], [np.mean(avg_effect),
np.mean(avg_effect)], 'k', linestyle='--')
ax.errorbar(
np.array(range(8)),
school_effects_med,
yerr=[
school_effects_med - school_effects_low,
school_effects_hi - school_effects_med
],
fmt='none')
ax.legend(('avg_effect', 'HMC', 'Observed effect'), fontsize=14)
plt.xlabel('School')
plt.ylabel('Treatment effect')
plt.title('HMC estimated school treatment effects vs. observed data')
fig.set_size_inches(10, 8)
plt.show()
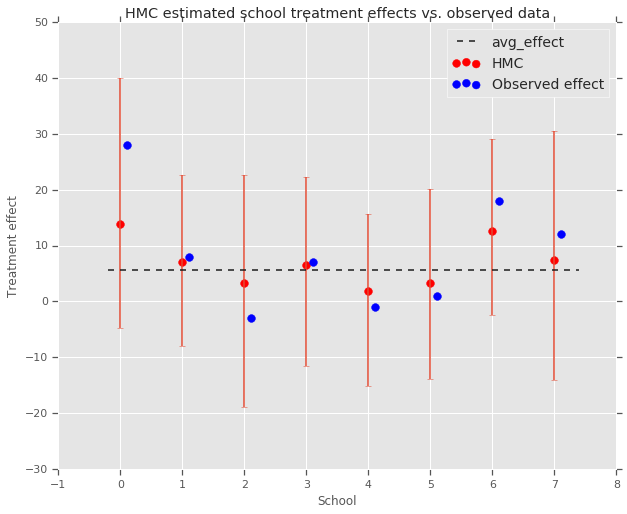
Possiamo osservare il restringimento verso il gruppo avg_effect sopra.
print("Inferred posterior mean: {0:.2f}".format(
np.mean(school_effects_samples[:,])))
print("Inferred posterior mean se: {0:.2f}".format(
np.std(school_effects_samples[:,])))
Inferred posterior mean: 6.97 Inferred posterior mean se: 10.41
Critica
Per ottenere la distribuzione predittiva posteriori, vale a dire, un modello di nuovi dati \(y^*\) data la osservata dati \(y\):
\[ p(y^*|y) \propto \int_\theta p(y^* | \theta)p(\theta |y)d\theta\]
ridefiniamo i valori delle variabili casuali nel modello di metterli alla media della distribuzione a posteriori, e il campione da quel modello per generare nuovi dati \(y^*\).
sample_shape = [5000]
_, _, _, predictive_treatment_effects = model.sample(
value=(tf.broadcast_to(np.mean(avg_effect, 0), sample_shape),
tf.broadcast_to(np.mean(avg_stddev, 0), sample_shape),
tf.broadcast_to(np.mean(school_effects_standard, 0),
sample_shape + [num_schools]),
None))
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(predictive_treatment_effects[:, 2*i].numpy(),
ax=ax[0], shade=True)
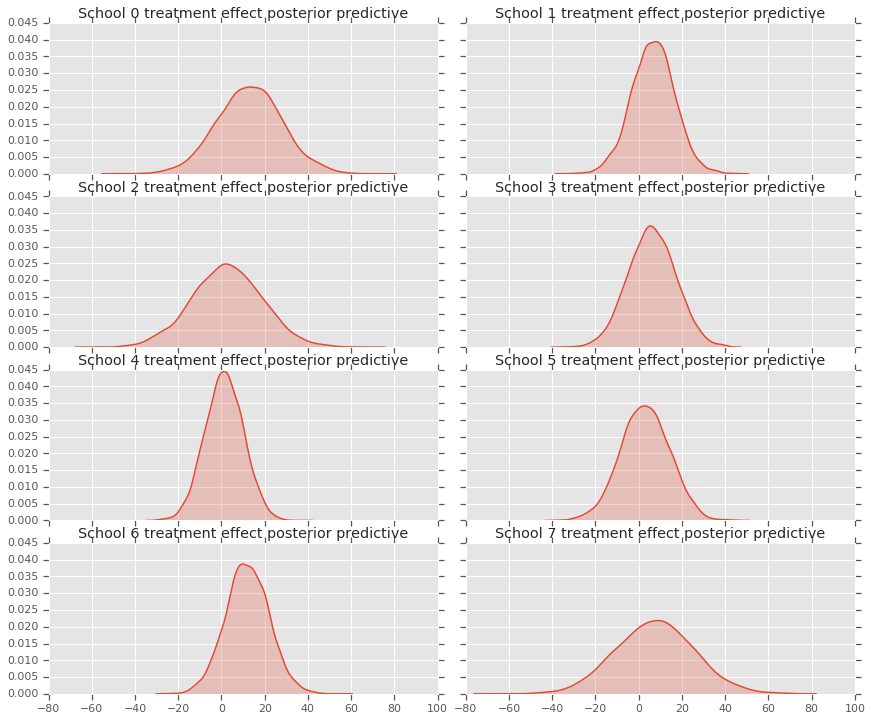
ax[0].title.set_text(
"School {} treatment effect posterior predictive".format(2*i))
sns.kdeplot(predictive_treatment_effects[:, 2*i + 1].numpy(),
ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect posterior predictive".format(2*i + 1))
plt.show()
# The mean predicted treatment effects for each of the eight schools.
prediction = np.mean(predictive_treatment_effects, axis=0)
Possiamo guardare i residui tra i dati sugli effetti del trattamento e le previsioni del modello a posteriori. Questi corrispondono al grafico sopra che mostra la contrazione degli effetti stimati verso la media della popolazione.
treatment_effects - prediction
array([14.905351 , 1.2838383, -5.6966295, 0.8327627, -2.3356671,
-2.0363257, 5.997898 , 4.3731265], dtype=float32)
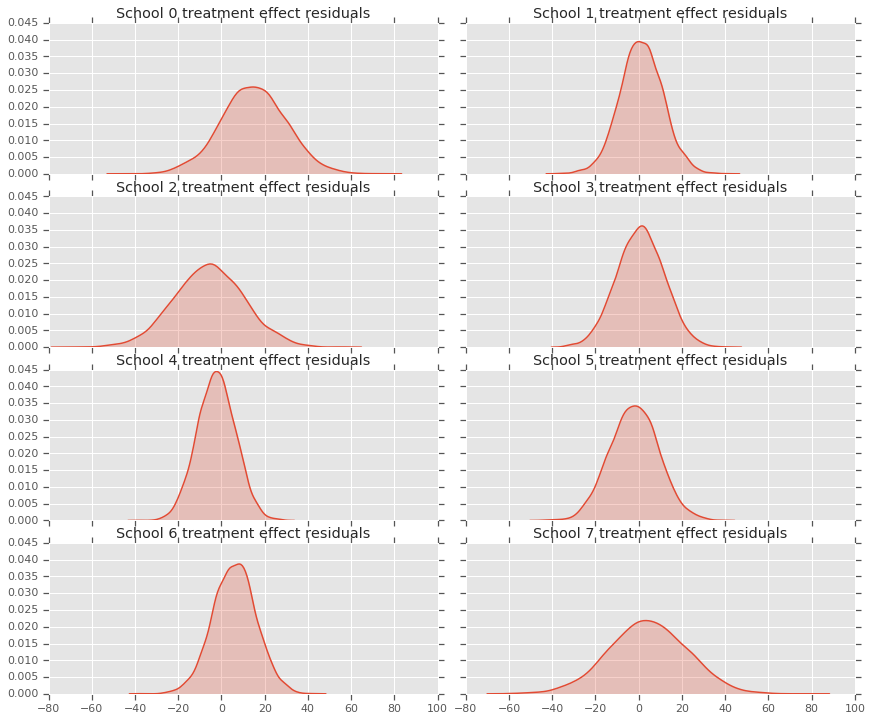
Poiché abbiamo una distribuzione delle previsioni per ogni scuola, possiamo considerare anche la distribuzione dei residui.
residuals = treatment_effects - predictive_treatment_effects
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(residuals[:, 2*i].numpy(), ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect residuals".format(2*i))
sns.kdeplot(residuals[:, 2*i + 1].numpy(), ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect residuals".format(2*i + 1))
plt.show()
Ringraziamenti
Questo tutorial è stato originariamente scritto in Edward 1.0 ( fonte ). Ringraziamo tutti coloro che hanno contribuito alla stesura e alla revisione di tale versione.
Riferimenti
- Donald B. Rubin. Stima in esperimenti randomizzati paralleli. Journal of Educational Statistics, 6(4):377-401, 1981.
- Andrew Gelman, John Carlin, Hal Stern, David Dunson, Aki Vehtari e Donald Rubin. Analisi dei dati bayesiani, terza edizione. Chapman e Hall/CRC, 2013.
