 TensorFlow.org पर देखें TensorFlow.org पर देखें |  Google Colab में चलाएं Google Colab में चलाएं |  GitHub पर स्रोत देखें GitHub पर स्रोत देखें |  नोटबुक डाउनलोड करें नोटबुक डाउनलोड करें |
आठ स्कूलों समस्या ( रुबिन 1981 ) आठ स्कूलों में समानांतर में आयोजित सैट कोचिंग कार्यक्रमों के प्रभाव को समझता है। यह एक क्लासिक समस्या (बन गया है बायेसियन डेटा विश्लेषण , स्टेन ) कि विनिमय समूहों के बीच जानकारी साझा करने के लिए श्रेणीबद्ध मॉडलिंग की उपयोगिता को दिखाता है।
नीचे अंतर्गत प्रयोग एक एडवर्ड 1.0 का रूपांतरण है ट्यूटोरियल ।
आयात
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
import warnings
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
आंकड़ा
बायेसियन डेटा एनालिसिस से, सेक्शन 5.5 (जेलमैन एट अल। 2013):
आठ उच्च विद्यालयों में से प्रत्येक में SAT-V (शैक्षिक योग्यता परीक्षण-मौखिक) के लिए विशेष कोचिंग कार्यक्रमों के प्रभावों का विश्लेषण करने के लिए शैक्षिक परीक्षण सेवा के लिए एक अध्ययन किया गया था। प्रत्येक अध्ययन में परिणाम चर SAT-V के एक विशेष प्रशासन पर स्कोर था, शैक्षिक परीक्षण सेवा द्वारा प्रशासित एक मानकीकृत बहुविकल्पी परीक्षा और कॉलेजों को प्रवेश निर्णय लेने में मदद करने के लिए उपयोग किया जाता है; स्कोर 200 और 800 के बीच भिन्न हो सकते हैं, औसत लगभग 500 और मानक विचलन लगभग 100 के साथ। एसएटी परीक्षाओं को विशेष रूप से परीक्षण पर प्रदर्शन में सुधार के लिए निर्देशित अल्पकालिक प्रयासों के प्रतिरोधी होने के लिए डिज़ाइन किया गया है; इसके बजाय वे कई वर्षों की शिक्षा में अर्जित ज्ञान और विकसित क्षमताओं को प्रतिबिंबित करने के लिए डिज़ाइन किए गए हैं। फिर भी, इस अध्ययन के आठ स्कूलों में से प्रत्येक ने अपने अल्पकालिक कोचिंग कार्यक्रम को SAT स्कोर बढ़ाने में बहुत सफल माना। साथ ही, यह मानने का कोई पूर्व कारण नहीं था कि आठ कार्यक्रमों में से कोई भी किसी अन्य की तुलना में अधिक प्रभावी था या कुछ किसी अन्य की तुलना में एक दूसरे के प्रभाव में अधिक समान थे।
आठ स्कूलों (से प्रत्येक के लिए\(J = 8\)), हम एक अनुमान के अनुसार उपचार प्रभाव है \(y_j\) और प्रभाव का अनुमान है की एक मानक त्रुटि \(\sigma_j\)। अध्ययन में उपचार प्रभाव पीएसएटी-एम और पीएसएटी-वी स्कोर को नियंत्रण चर के रूप में उपयोग करके उपचार समूह पर एक रैखिक प्रतिगमन द्वारा प्राप्त किया गया था। वहाँ के रूप में कोई पूर्व धारणा यह थी कि स्कूलों में से किसी भी कम या ज्यादा समान या कि कोचिंग कार्यक्रमों में से किसी भी अधिक प्रभावी होगा थे, हम के रूप में उपचार प्रभाव पर विचार कर सकते विनिमय ।
num_schools = 8 # number of schools
treatment_effects = np.array(
[28, 8, -3, 7, -1, 1, 18, 12], dtype=np.float32) # treatment effects
treatment_stddevs = np.array(
[15, 10, 16, 11, 9, 11, 10, 18], dtype=np.float32) # treatment SE
fig, ax = plt.subplots()
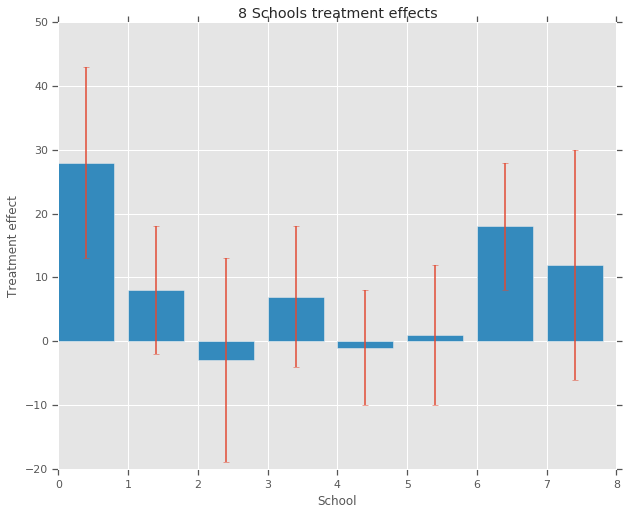
plt.bar(range(num_schools), treatment_effects, yerr=treatment_stddevs)
plt.title("8 Schools treatment effects")
plt.xlabel("School")
plt.ylabel("Treatment effect")
fig.set_size_inches(10, 8)
plt.show()
नमूना
डेटा कैप्चर करने के लिए, हम एक श्रेणीबद्ध सामान्य मॉडल का उपयोग करते हैं। यह जनन प्रक्रिया का अनुसरण करता है,
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i \sim \text{Normal}\left(\text{loc}{=}\mu,\ \text{scale}{=}\tau \right) \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
जहां \(\mu\) पहले औसत उपचार के प्रभाव और का प्रतिनिधित्व करता है \(\tau\) नियंत्रण कितना विचरण वहाँ स्कूलों के बीच है। \(y_i\) और \(\sigma_i\) मनाया जाता है। के रूप में \(\tau \rightarrow \infty\), मॉडल कोई-पूलिंग मॉडल, यानी पास जाते है, स्कूल उपचार के प्रभाव का अनुमान है में से प्रत्येक के अधिक स्वतंत्र होने के लिए अनुमति दी जाती है। के रूप में \(\tau \rightarrow 0\), पूरा मॉडल-पूलिंग मॉडल, यानी पास जाते है, स्कूल उपचार प्रभाव के सभी समूह औसत के करीब हैं \(\mu\)। सकारात्मक होने के मानक विचलन प्रतिबंधित करने के लिए, हम आकर्षित \(\tau\) एक lognormal वितरण (जो ड्राइंग के बराबर है से \(log(\tau)\) एक सामान्य वितरण से)।
बाद Divergences साथ निदान पक्षपातपूर्ण निष्कर्ष है, हम एक बराबर गैर केंद्रित मॉडल में ऊपर मॉडल को बदलने:
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i' \sim \text{Normal}\left(\text{loc}{=}0,\ \text{scale}{=}1 \right) \\ & \theta_i = \mu + \tau \theta_i' \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
हम इस मॉडल एक के रूप में वस्तु के बारे में जैसे सोचना JointDistributionSequential उदाहरण:
model = tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=10., name="avg_effect"), # `mu` above
tfd.Normal(loc=5., scale=1., name="avg_stddev"), # `log(tau)` above
tfd.Independent(tfd.Normal(loc=tf.zeros(num_schools),
scale=tf.ones(num_schools),
name="school_effects_standard"), # `theta_prime`
reinterpreted_batch_ndims=1),
lambda school_effects_standard, avg_stddev, avg_effect: (
tfd.Independent(tfd.Normal(loc=(avg_effect[..., tf.newaxis] +
tf.exp(avg_stddev[..., tf.newaxis]) *
school_effects_standard), # `theta` above
scale=treatment_stddevs),
name="treatment_effects", # `y` above
reinterpreted_batch_ndims=1))
])
def target_log_prob_fn(avg_effect, avg_stddev, school_effects_standard):
"""Unnormalized target density as a function of states."""
return model.log_prob((
avg_effect, avg_stddev, school_effects_standard, treatment_effects))
बायेसियन अनुमान
डेटा को देखते हुए, हम मॉडल के मापदंडों पर पश्च वितरण की गणना करने के लिए हैमिल्टनियन मोंटे कार्लो (HMC) का प्रदर्शन करते हैं।
num_results = 5000
num_burnin_steps = 3000
# Improve performance by tracing the sampler using `tf.function`
# and compiling it using XLA.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
tf.zeros([], name='init_avg_effect'),
tf.zeros([], name='init_avg_stddev'),
tf.ones([num_schools], name='init_school_effects_standard'),
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.4,
num_leapfrog_steps=3))
states, kernel_results = do_sampling()
avg_effect, avg_stddev, school_effects_standard = states
school_effects_samples = (
avg_effect[:, np.newaxis] +
np.exp(avg_stddev)[:, np.newaxis] * school_effects_standard)
num_accepted = np.sum(kernel_results.is_accepted)
print('Acceptance rate: {}'.format(num_accepted / num_results))
Acceptance rate: 0.5974
fig, axes = plt.subplots(8, 2, sharex='col', sharey='col')
fig.set_size_inches(12, 10)
for i in range(num_schools):
axes[i][0].plot(school_effects_samples[:,i].numpy())
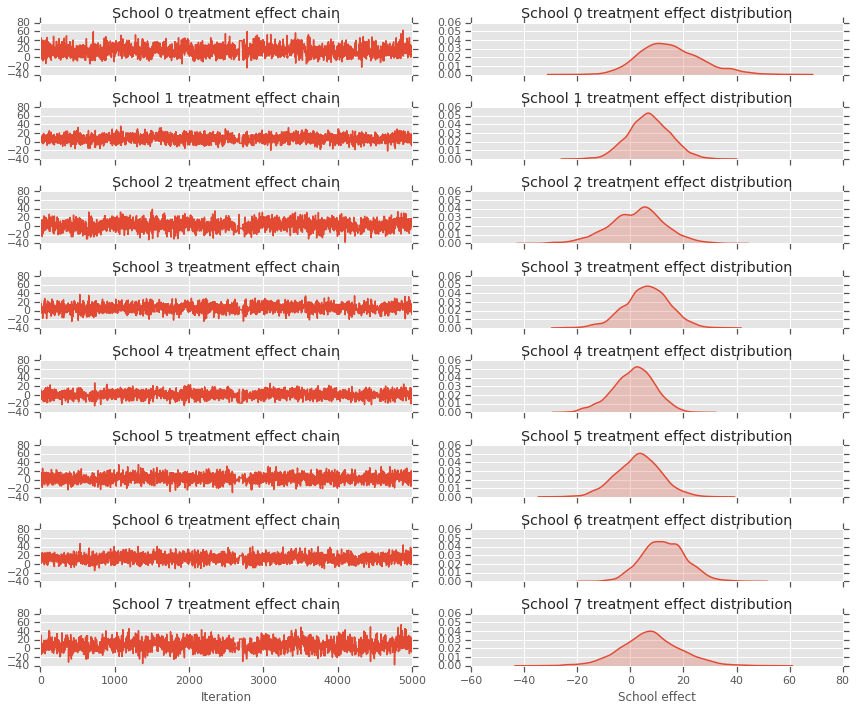
axes[i][0].title.set_text("School {} treatment effect chain".format(i))
sns.kdeplot(school_effects_samples[:,i].numpy(), ax=axes[i][1], shade=True)
axes[i][1].title.set_text("School {} treatment effect distribution".format(i))
axes[num_schools - 1][0].set_xlabel("Iteration")
axes[num_schools - 1][1].set_xlabel("School effect")
fig.tight_layout()
plt.show()
print("E[avg_effect] = {}".format(np.mean(avg_effect)))
print("E[avg_stddev] = {}".format(np.mean(avg_stddev)))
print("E[school_effects_standard] =")
print(np.mean(school_effects_standard[:, ]))
print("E[school_effects] =")
print(np.mean(school_effects_samples[:, ], axis=0))
E[avg_effect] = 5.57183933258 E[avg_stddev] = 2.47738981247 E[school_effects_standard] = 0.08509017 E[school_effects] = [15.0051 7.103311 2.4552586 6.2744603 1.3364682 3.1125953 12.762501 7.743602 ]
# Compute the 95% interval for school_effects
school_effects_low = np.array([
np.percentile(school_effects_samples[:, i], 2.5) for i in range(num_schools)
])
school_effects_med = np.array([
np.percentile(school_effects_samples[:, i], 50) for i in range(num_schools)
])
school_effects_hi = np.array([
np.percentile(school_effects_samples[:, i], 97.5)
for i in range(num_schools)
])
fig, ax = plt.subplots(nrows=1, ncols=1, sharex=True)
ax.scatter(np.array(range(num_schools)), school_effects_med, color='red', s=60)
ax.scatter(
np.array(range(num_schools)) + 0.1, treatment_effects, color='blue', s=60)
plt.plot([-0.2, 7.4], [np.mean(avg_effect),
np.mean(avg_effect)], 'k', linestyle='--')
ax.errorbar(
np.array(range(8)),
school_effects_med,
yerr=[
school_effects_med - school_effects_low,
school_effects_hi - school_effects_med
],
fmt='none')
ax.legend(('avg_effect', 'HMC', 'Observed effect'), fontsize=14)
plt.xlabel('School')
plt.ylabel('Treatment effect')
plt.title('HMC estimated school treatment effects vs. observed data')
fig.set_size_inches(10, 8)
plt.show()
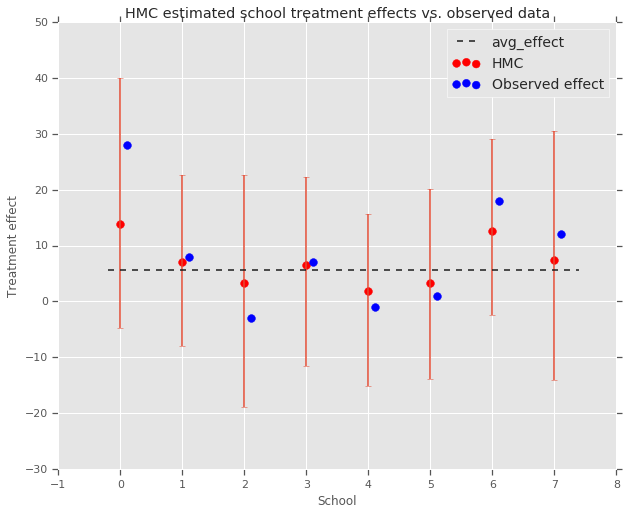
हम समूह की ओर दबाव का निरीक्षण कर सकते avg_effect ऊपर।
print("Inferred posterior mean: {0:.2f}".format(
np.mean(school_effects_samples[:,])))
print("Inferred posterior mean se: {0:.2f}".format(
np.std(school_effects_samples[:,])))
Inferred posterior mean: 6.97 Inferred posterior mean se: 10.41
आलोचना
पीछे भविष्य कहनेवाला वितरण, यानी, नए आंकड़ों का एक मॉडल प्राप्त करने के लिए \(y^*\) मनाया डेटा दिया \(y\):
\[ p(y^*|y) \propto \int_\theta p(y^* | \theta)p(\theta |y)d\theta\]
हम उन्हें है कि मॉडल से पिछला वितरण, और नमूना की औसत करने के लिए सेट करने के लिए नए डेटा उत्पन्न करने के लिए मॉडल में यादृच्छिक चर के मूल्यों को भी पार \(y^*\)।
sample_shape = [5000]
_, _, _, predictive_treatment_effects = model.sample(
value=(tf.broadcast_to(np.mean(avg_effect, 0), sample_shape),
tf.broadcast_to(np.mean(avg_stddev, 0), sample_shape),
tf.broadcast_to(np.mean(school_effects_standard, 0),
sample_shape + [num_schools]),
None))
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(predictive_treatment_effects[:, 2*i].numpy(),
ax=ax[0], shade=True)
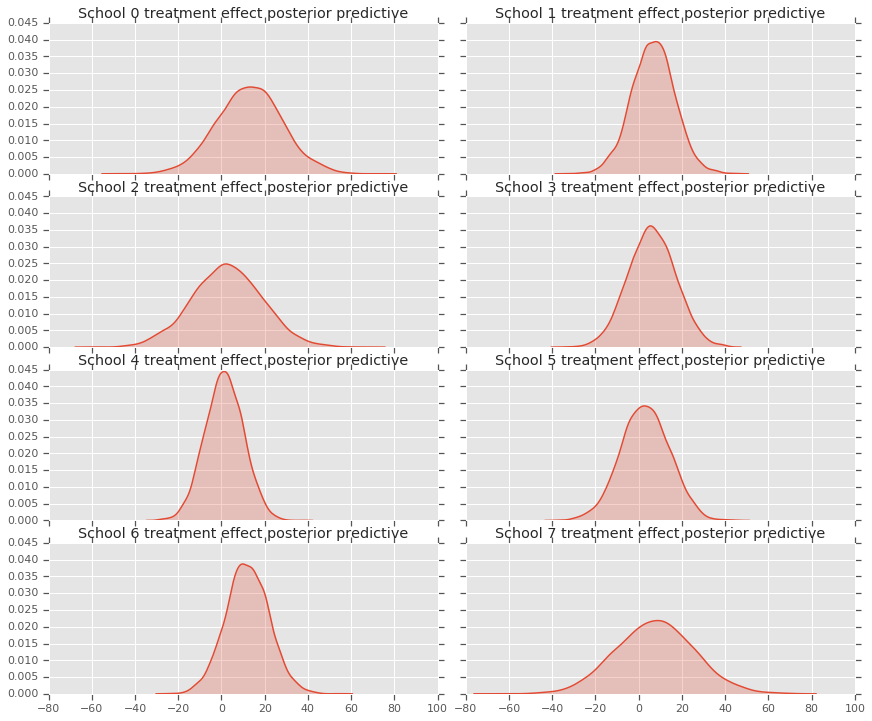
ax[0].title.set_text(
"School {} treatment effect posterior predictive".format(2*i))
sns.kdeplot(predictive_treatment_effects[:, 2*i + 1].numpy(),
ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect posterior predictive".format(2*i + 1))
plt.show()
# The mean predicted treatment effects for each of the eight schools.
prediction = np.mean(predictive_treatment_effects, axis=0)
हम उपचार प्रभाव डेटा और मॉडल पोस्टीरियर की भविष्यवाणियों के बीच के अवशेषों को देख सकते हैं। ये ऊपर की साजिश के अनुरूप हैं जो जनसंख्या औसत की ओर अनुमानित प्रभावों के सिकुड़न को दर्शाता है।
treatment_effects - prediction
array([14.905351 , 1.2838383, -5.6966295, 0.8327627, -2.3356671,
-2.0363257, 5.997898 , 4.3731265], dtype=float32)
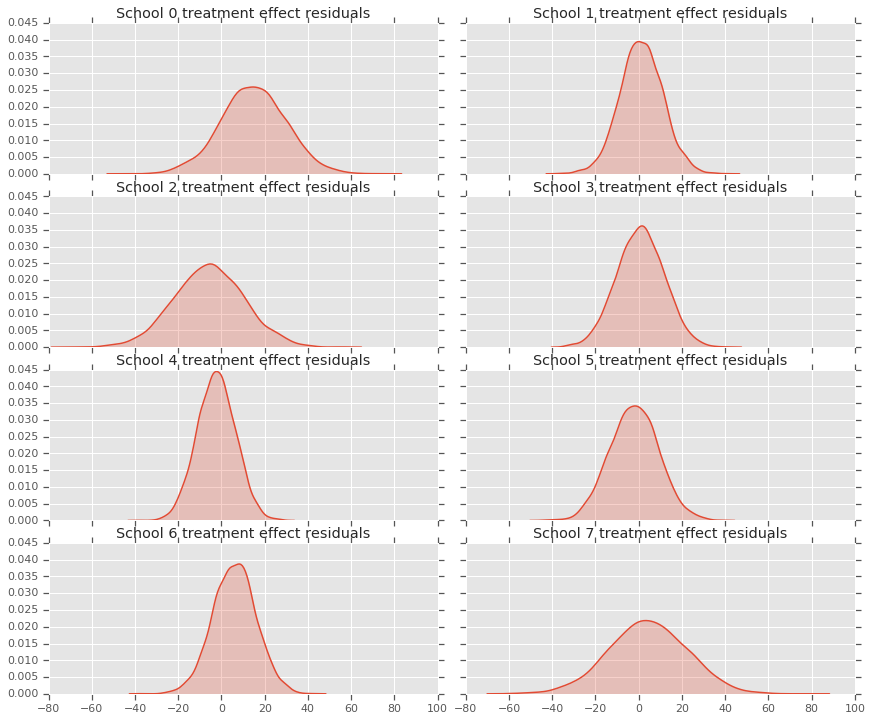
चूंकि हमारे पास प्रत्येक स्कूल के लिए भविष्यवाणियों का वितरण है, इसलिए हम अवशिष्टों के वितरण पर भी विचार कर सकते हैं।
residuals = treatment_effects - predictive_treatment_effects
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(residuals[:, 2*i].numpy(), ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect residuals".format(2*i))
sns.kdeplot(residuals[:, 2*i + 1].numpy(), ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect residuals".format(2*i + 1))
plt.show()
स्वीकृतियाँ
इस ट्यूटोरियल मूल रूप से एडवर्ड 1.0 (में लिखा गया था स्रोत )। हम उस संस्करण को लिखने और संशोधित करने के लिए सभी योगदानकर्ताओं को धन्यवाद देते हैं।
संदर्भ
- डोनाल्ड बी रुबिन। समानांतर यादृच्छिक प्रयोगों में अनुमान। जर्नल ऑफ़ एजुकेशनल स्टैटिस्टिक्स, 6(4):377-401, 1981।
- एंड्रयू गेलमैन, जॉन कार्लिन, हैल स्टर्न, डेविड डनसन, अकी वेहटारी और डोनाल्ड रुबिन। बायेसियन डेटा विश्लेषण, तीसरा संस्करण। चैपमैन और हॉल/सीआरसी, 2013।
