 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Les huit écoles problème ( Rubin 1981 ) considère que l'efficacité des programmes de coaching SAT menées en parallèle à huit écoles. Il est devenu un problème classique ( Bayesian Data Analysis , Stan ) qui illustre l'utilité de la modélisation hiérarchique pour le partage d' informations entre les groupes échangeables.
Le implemention ci - dessous est une adaptation d'un Edward 1,0 tutoriel .
Importations
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
import warnings
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
Les données
De l'analyse de données bayésienne, section 5.5 (Gelman et al. 2013) :
Une étude a été réalisée pour l'Educational Testing Service afin d'analyser les effets des programmes de coaching spéciaux pour le SAT-V (Scholastic Aptitude Test-Verbal) dans chacune des huit écoles secondaires. La variable de résultat dans chaque étude était le score à une administration spéciale du SAT-V, un test à choix multiples standardisé administré par le Educational Testing Service et utilisé pour aider les collèges à prendre des décisions d'admission ; les scores peuvent varier entre 200 et 800, avec une moyenne d'environ 500 et un écart type d'environ 100. Les examens SAT sont conçus pour résister aux efforts à court terme visant spécifiquement à améliorer les performances au test ; ils sont plutôt conçus pour refléter les connaissances acquises et les capacités développées au cours de nombreuses années d'éducation. Néanmoins, chacune des huit écoles de cette étude considérait que son programme de coaching à court terme réussissait très bien à augmenter les scores SAT. De plus, il n'y avait aucune raison préalable de croire que l'un des huit programmes était plus efficace que n'importe quel autre ou que certains avaient des effets plus similaires les uns aux autres qu'à n'importe quel autre.
Pour chacune des huit écoles (\(J = 8\)), nous avons un effet de traitement estimé \(y_j\) et une erreur standard de l'estimation de l' effet \(\sigma_j\). Les effets du traitement dans l'étude ont été obtenus par une régression linéaire sur le groupe de traitement en utilisant les scores PSAT-M et PSAT-V comme variables de contrôle. Comme il n'y avait pas de croyance avant que l' une des écoles étaient plus ou moins similaires ou que l' un des programmes que nous pouvons considérer de coaching serait plus efficace, les effets du traitement comme échangeables .
num_schools = 8 # number of schools
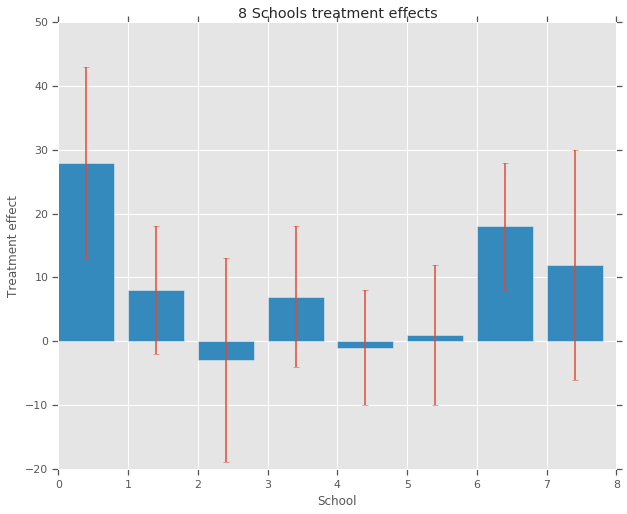
treatment_effects = np.array(
[28, 8, -3, 7, -1, 1, 18, 12], dtype=np.float32) # treatment effects
treatment_stddevs = np.array(
[15, 10, 16, 11, 9, 11, 10, 18], dtype=np.float32) # treatment SE
fig, ax = plt.subplots()
plt.bar(range(num_schools), treatment_effects, yerr=treatment_stddevs)
plt.title("8 Schools treatment effects")
plt.xlabel("School")
plt.ylabel("Treatment effect")
fig.set_size_inches(10, 8)
plt.show()
Modèle
Pour capturer les données, nous utilisons un modèle normal hiérarchique. Il suit le processus génératif,
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i \sim \text{Normal}\left(\text{loc}{=}\mu,\ \text{scale}{=}\tau \right) \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
où \(\mu\) représente l'effet du traitement moyen avant et \(\tau\) contrôle combien la variance il y a entre les écoles. Le \(y_i\) et \(\sigma_i\) sont respectées. Comme \(\tau \rightarrow \infty\), le modèle se rapproche du modèle sans mise en commun, à savoir, chacune des estimations de l' effet du traitement scolaire sont autorisés à être plus indépendants. Comme \(\tau \rightarrow 0\), le modèle se rapproche du modèle complet mise en commun, à savoir tous les effets du traitement scolaire sont plus proches du groupe moyen \(\mu\). Pour limiter l'écart - type positif, nous attirons \(\tau\) d'une distribution log - normale ( ce qui équivaut à dessin \(log(\tau)\) à partir d' une distribution normale).
A la suite Diagnostiquer Biased avec Inference Divergences , nous transformons le modèle ci - dessus en un équivalent modèle de non-centré:
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i' \sim \text{Normal}\left(\text{loc}{=}0,\ \text{scale}{=}1 \right) \\ & \theta_i = \mu + \tau \theta_i' \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
Nous réifier ce modèle comme JointDistributionSequential exemple:
model = tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=10., name="avg_effect"), # `mu` above
tfd.Normal(loc=5., scale=1., name="avg_stddev"), # `log(tau)` above
tfd.Independent(tfd.Normal(loc=tf.zeros(num_schools),
scale=tf.ones(num_schools),
name="school_effects_standard"), # `theta_prime`
reinterpreted_batch_ndims=1),
lambda school_effects_standard, avg_stddev, avg_effect: (
tfd.Independent(tfd.Normal(loc=(avg_effect[..., tf.newaxis] +
tf.exp(avg_stddev[..., tf.newaxis]) *
school_effects_standard), # `theta` above
scale=treatment_stddevs),
name="treatment_effects", # `y` above
reinterpreted_batch_ndims=1))
])
def target_log_prob_fn(avg_effect, avg_stddev, school_effects_standard):
"""Unnormalized target density as a function of states."""
return model.log_prob((
avg_effect, avg_stddev, school_effects_standard, treatment_effects))
Inférence bayésienne
Compte tenu des données, nous effectuons un Monte Carlo hamiltonien (HMC) pour calculer la distribution postérieure sur les paramètres du modèle.
num_results = 5000
num_burnin_steps = 3000
# Improve performance by tracing the sampler using `tf.function`
# and compiling it using XLA.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
tf.zeros([], name='init_avg_effect'),
tf.zeros([], name='init_avg_stddev'),
tf.ones([num_schools], name='init_school_effects_standard'),
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.4,
num_leapfrog_steps=3))
states, kernel_results = do_sampling()
avg_effect, avg_stddev, school_effects_standard = states
school_effects_samples = (
avg_effect[:, np.newaxis] +
np.exp(avg_stddev)[:, np.newaxis] * school_effects_standard)
num_accepted = np.sum(kernel_results.is_accepted)
print('Acceptance rate: {}'.format(num_accepted / num_results))
Acceptance rate: 0.5974
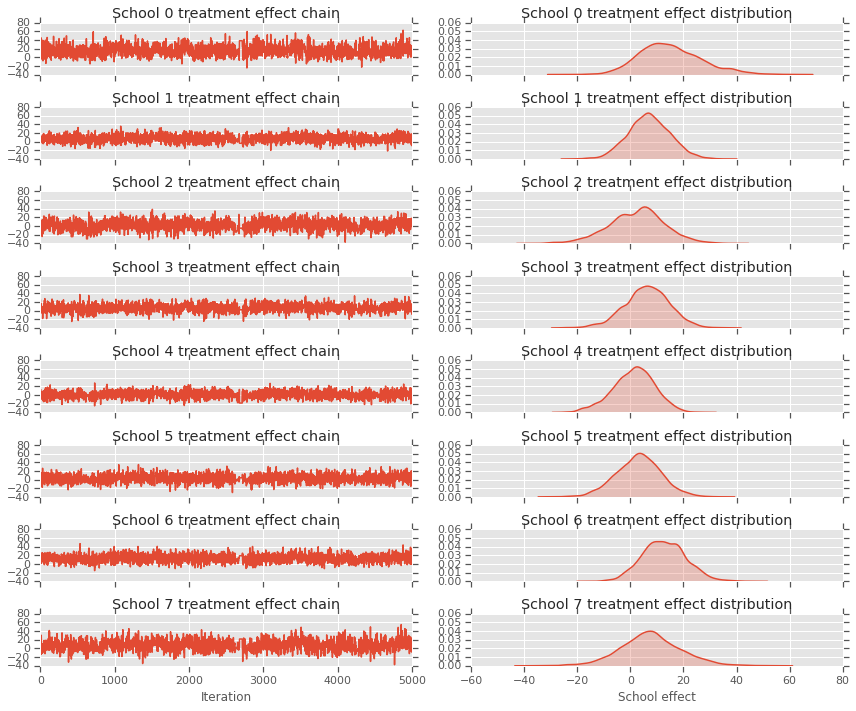
fig, axes = plt.subplots(8, 2, sharex='col', sharey='col')
fig.set_size_inches(12, 10)
for i in range(num_schools):
axes[i][0].plot(school_effects_samples[:,i].numpy())
axes[i][0].title.set_text("School {} treatment effect chain".format(i))
sns.kdeplot(school_effects_samples[:,i].numpy(), ax=axes[i][1], shade=True)
axes[i][1].title.set_text("School {} treatment effect distribution".format(i))
axes[num_schools - 1][0].set_xlabel("Iteration")
axes[num_schools - 1][1].set_xlabel("School effect")
fig.tight_layout()
plt.show()
print("E[avg_effect] = {}".format(np.mean(avg_effect)))
print("E[avg_stddev] = {}".format(np.mean(avg_stddev)))
print("E[school_effects_standard] =")
print(np.mean(school_effects_standard[:, ]))
print("E[school_effects] =")
print(np.mean(school_effects_samples[:, ], axis=0))
E[avg_effect] = 5.57183933258 E[avg_stddev] = 2.47738981247 E[school_effects_standard] = 0.08509017 E[school_effects] = [15.0051 7.103311 2.4552586 6.2744603 1.3364682 3.1125953 12.762501 7.743602 ]
# Compute the 95% interval for school_effects
school_effects_low = np.array([
np.percentile(school_effects_samples[:, i], 2.5) for i in range(num_schools)
])
school_effects_med = np.array([
np.percentile(school_effects_samples[:, i], 50) for i in range(num_schools)
])
school_effects_hi = np.array([
np.percentile(school_effects_samples[:, i], 97.5)
for i in range(num_schools)
])
fig, ax = plt.subplots(nrows=1, ncols=1, sharex=True)
ax.scatter(np.array(range(num_schools)), school_effects_med, color='red', s=60)
ax.scatter(
np.array(range(num_schools)) + 0.1, treatment_effects, color='blue', s=60)
plt.plot([-0.2, 7.4], [np.mean(avg_effect),
np.mean(avg_effect)], 'k', linestyle='--')
ax.errorbar(
np.array(range(8)),
school_effects_med,
yerr=[
school_effects_med - school_effects_low,
school_effects_hi - school_effects_med
],
fmt='none')
ax.legend(('avg_effect', 'HMC', 'Observed effect'), fontsize=14)
plt.xlabel('School')
plt.ylabel('Treatment effect')
plt.title('HMC estimated school treatment effects vs. observed data')
fig.set_size_inches(10, 8)
plt.show()
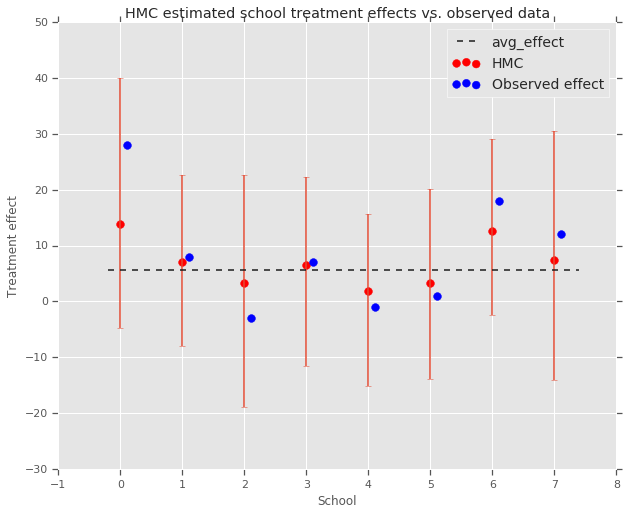
Nous pouvons observer le retrait vers le groupe avg_effect ci - dessus.
print("Inferred posterior mean: {0:.2f}".format(
np.mean(school_effects_samples[:,])))
print("Inferred posterior mean se: {0:.2f}".format(
np.std(school_effects_samples[:,])))
Inferred posterior mean: 6.97 Inferred posterior mean se: 10.41
Critique
Pour obtenir la distribution prédictive a posteriori, par exemple, un modèle de nouvelles données \(y^*\) compte tenu des données observées \(y\):
\[ p(y^*|y) \propto \int_\theta p(y^* | \theta)p(\theta |y)d\theta\]
nous remplaçons les valeurs des variables aléatoires dans le modèle pour les mettre à la moyenne de la distribution postérieure et de l' échantillon à partir de ce modèle pour générer de nouvelles données \(y^*\).
sample_shape = [5000]
_, _, _, predictive_treatment_effects = model.sample(
value=(tf.broadcast_to(np.mean(avg_effect, 0), sample_shape),
tf.broadcast_to(np.mean(avg_stddev, 0), sample_shape),
tf.broadcast_to(np.mean(school_effects_standard, 0),
sample_shape + [num_schools]),
None))
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(predictive_treatment_effects[:, 2*i].numpy(),
ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect posterior predictive".format(2*i))
sns.kdeplot(predictive_treatment_effects[:, 2*i + 1].numpy(),
ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect posterior predictive".format(2*i + 1))
plt.show()
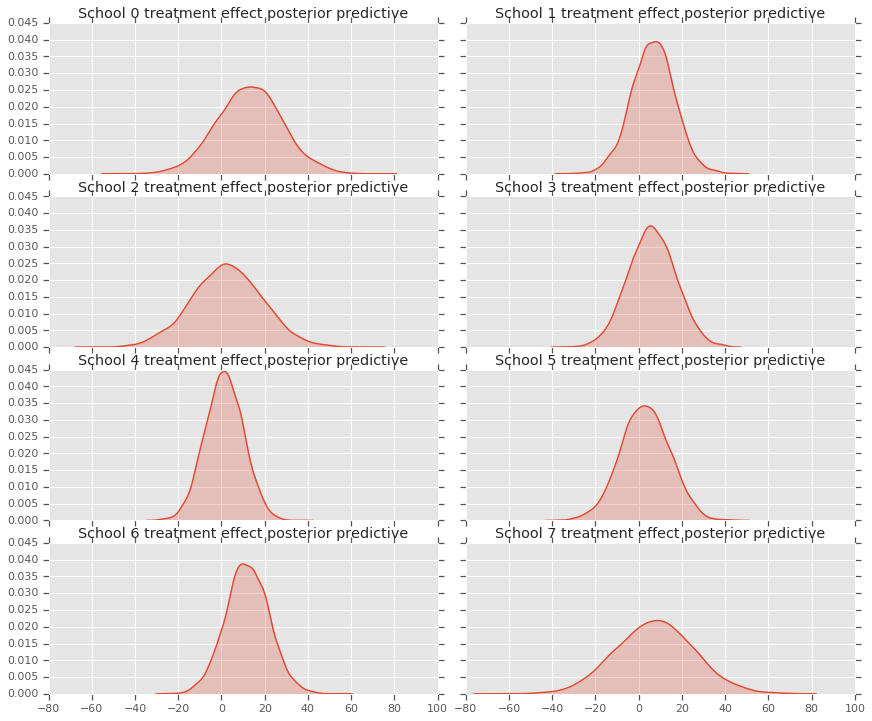
# The mean predicted treatment effects for each of the eight schools.
prediction = np.mean(predictive_treatment_effects, axis=0)
Nous pouvons examiner les résidus entre les données sur les effets du traitement et les prédictions du modèle a posteriori. Ceux-ci correspondent au graphique ci-dessus qui montre le rétrécissement des effets estimés vers la moyenne de la population.
treatment_effects - prediction
array([14.905351 , 1.2838383, -5.6966295, 0.8327627, -2.3356671,
-2.0363257, 5.997898 , 4.3731265], dtype=float32)
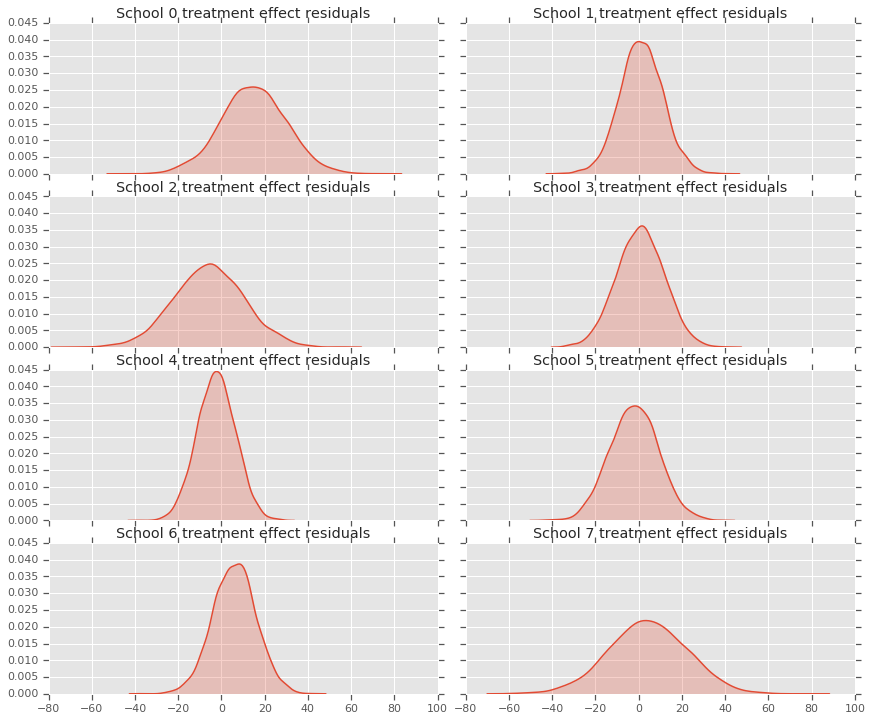
Comme nous avons une distribution des prédictions pour chaque école, nous pouvons également considérer la distribution des résidus.
residuals = treatment_effects - predictive_treatment_effects
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(residuals[:, 2*i].numpy(), ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect residuals".format(2*i))
sns.kdeplot(residuals[:, 2*i + 1].numpy(), ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect residuals".format(2*i + 1))
plt.show()
Remerciements
Ce tutoriel a été écrit dans Edward 1.0 ( source de ). Nous remercions tous ceux qui ont contribué à la rédaction et à la révision de cette version.
Les références
- Donald B. Rubin. Estimation dans des expériences randomisées parallèles. Journal of Educational Statistics, 6(4):377-401, 1981.
- Andrew Gelman, John Carlin, Hal Stern, David Dunson, Aki Vehtari et Donald Rubin. Analyse de données bayésienne, troisième édition. Chapman et Hall/CRC, 2013.
