 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
TensorFlow Probability (TFP) trên JAX hiện có các công cụ cho tính toán số phân tán. Để mở rộng quy mô đến số lượng lớn các máy gia tốc, các công cụ được xây dựng xoay quanh việc viết mã bằng cách sử dụng mô hình "đa dữ liệu chương trình đơn", viết tắt là SPMD.
Trong sổ tay này, chúng ta sẽ xem xét cách "suy nghĩ trong SPMD" và giới thiệu các bản tóm tắt TFP mới để mở rộng cho các cấu hình như TPU pod hoặc các cụm GPU. Nếu bạn đang tự chạy mã này, hãy đảm bảo chọn thời gian chạy TPU.
Trước tiên, chúng tôi sẽ cài đặt các phiên bản mới nhất TFP, JAX và TF.
Số lượt cài đặt
pip install jaxlib --upgrade -q 2>&1 1> /dev/nullpip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/nullpip install tf-nightly-cpu -q -I 2>&1 1> /dev/nullpip install jax -I -q --upgrade 2>&1 1>/dev/null
Chúng tôi sẽ nhập một số thư viện chung, cùng với một số tiện ích JAX.
Thiết lập và Nhập khẩu
import functools
import collections
import contextlib
import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds
from tensorflow_probability.substrates import jax as tfp
sns.set(style='white')
INFO:tensorflow:Enabling eager execution INFO:tensorflow:Enabling v2 tensorshape INFO:tensorflow:Enabling resource variables INFO:tensorflow:Enabling tensor equality INFO:tensorflow:Enabling control flow v2
Chúng tôi cũng sẽ thiết lập một số bí danh TFP tiện dụng. Các trừu tượng mới hiện đang được cung cấp trong tfp.experimental.distribute và tfp.experimental.mcmc .
tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc
Root = tfed.JointDistributionCoroutine.Root
Để kết nối sổ ghi chép với TPU, chúng tôi sử dụng trình trợ giúp sau từ JAX. Để xác nhận rằng chúng tôi đã kết nối, chúng tôi in ra số lượng thiết bị, phải là tám thiết bị.
from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')
Found 8 devices
Một giới thiệu vắn tắt jax.pmap
Sau khi kết nối với một TPU, chúng tôi được tiếp cận với tám điện thoại. Tuy nhiên, khi chúng tôi háo hức chạy mã JAX, JAX mặc định chỉ chạy các tính toán trên một mã.
Cách đơn giản nhất để thực hiện tính toán trên nhiều thiết bị là ánh xạ một chức năng, mỗi thiết bị thực thi một chỉ mục của bản đồ. JAX cung cấp jax.pmap ( "bản đồ song song") chuyển đổi mà biến một hàm thành một trong những bản đồ chức năng trên một số thiết bị.
Trong ví dụ sau, chúng tôi tạo một mảng có kích thước 8 (để phù hợp với số lượng thiết bị có sẵn) và ánh xạ một hàm có thêm 5 trên đó.
xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)
<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5. 6. 7. 8. 9. 10. 11. 12.]
Lưu ý rằng chúng tôi nhận được một ShardedDeviceArray loại trở lại, chỉ ra rằng các mảng đầu ra được thể chất tách giữa các thiết bị.
jax.pmap đóng vai trò ngữ nghĩa như một bản đồ, nhưng có một vài lựa chọn quan trọng là sửa đổi hành vi của nó. Theo mặc định, pmap giả định tất cả các yếu tố đầu vào chức năng đang được ánh xạ kết thúc, nhưng chúng ta có thể thay đổi hành vi này với in_axes tranh cãi.
xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)
[ 5. 6. 7. 8. 9. 10. 11. 12.]
Tương tự, các out_axes lập luận để pmap xác định có hay không để trả lại giá trị trên mọi thiết bị. Thiết out_axes để None tự động trả về giá trị trên thiết bị 1 và chỉ nên được sử dụng nếu chúng tôi tin tưởng các giá trị đều giống nhau trên mọi thiết bị.
xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)
2.0
Điều gì xảy ra khi những gì chúng ta muốn làm không thể diễn đạt dễ dàng như một hàm thuần túy được ánh xạ? Ví dụ, nếu chúng ta muốn tính tổng trên trục mà chúng ta đang lập bản đồ thì sao? JAX cung cấp "tập thể", các chức năng giao tiếp giữa các thiết bị, để cho phép viết các chương trình phân tán phức tạp và thú vị hơn. Để hiểu chính xác cách chúng hoạt động, chúng tôi sẽ giới thiệu SPMD.
SPMD là gì?
Đa dữ liệu chương trình đơn (SPMD) là mô hình lập trình đồng thời trong đó một chương trình (tức là cùng một mã) được thực thi đồng thời trên các thiết bị, nhưng đầu vào cho mỗi chương trình đang chạy có thể khác nhau.
Nếu chương trình của chúng tôi là một chức năng đơn giản của nguyên liệu đầu vào của nó (tức là một cái gì đó giống như x + 5 ), chạy một chương trình trong SPMD chỉ là lập bản đồ nó dữ liệu qua khác nhau, như chúng ta đã làm với jax.pmap trước đó. Tuy nhiên, chúng ta có thể làm nhiều hơn là chỉ "ánh xạ" một chức năng. JAX cung cấp "tập thể", là các chức năng giao tiếp giữa các thiết bị.
Ví dụ: có thể chúng tôi muốn lấy tổng một số lượng trên tất cả các thiết bị của mình. Trước khi chúng tôi làm điều đó, chúng ta cần phải gán một tên cho trục chúng tôi lập bản đồ đang trên trong pmap . Sau đó chúng tôi sử dụng lax.psum ( "tổng song song") chức năng để thực hiện một khoản tiền giữa các thiết bị, đảm bảo chúng tôi xác định được tên trục chúng tôi đang tổng hợp kết thúc.
def f(x):
out = lax.psum(x, axis_name='i')
return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)
ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)
Các psum uẩn tập thể giá trị của x trên mỗi thiết bị và đồng bộ hóa giá trị của nó trên bản đồ tức là out là 28. trên mỗi thiết bị. Chúng tôi không còn thực hiện một "bản đồ" đơn giản nữa, nhưng chúng tôi đang thực hiện một chương trình SPMD nơi tính toán của mỗi thiết bị giờ đây có thể tương tác với tính toán tương tự trên các thiết bị khác, mặc dù theo một cách hạn chế bằng cách sử dụng tập thể. Trong kịch bản này, chúng ta có thể sử dụng out_axes = None , bởi vì psum sẽ đồng bộ hóa các giá trị.
def f(x):
out = lax.psum(x, axis_name='i')
return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))
ShardedDeviceArray(28., dtype=float32)
SPMD cho phép chúng tôi viết đồng thời một chương trình chạy trên mọi thiết bị trong bất kỳ cấu hình TPU nào. Mã tương tự được sử dụng để thực hiện học máy trên 8 lõi TPU có thể được sử dụng trên một pod TPU có thể có hàng trăm đến hàng nghìn lõi! Để xem hướng dẫn chi tiết hơn về jax.pmap và SPMD, bạn có thể tham khảo các các JAX 101 hướng dẫn .
MCMC theo quy mô
Trong sổ tay này, chúng tôi tập trung vào việc sử dụng phương pháp Markov Chain Monte Carlo (MCMC) để suy luận Bayes. Có thể có nhiều cách chúng tôi sử dụng nhiều thiết bị cho MCMC, nhưng trong sổ tay này, chúng tôi sẽ tập trung vào hai:
- Chạy chuỗi Markov độc lập trên các thiết bị khác nhau. Trường hợp này khá đơn giản và có thể làm được với TFP vani.
- Làm sắc nét một tập dữ liệu trên các thiết bị. Trường hợp này phức tạp hơn một chút và yêu cầu máy móc TFP được bổ sung gần đây.
Chuỗi độc lập
Giả sử chúng tôi muốn thực hiện suy luận Bayes về một vấn đề bằng MCMC và muốn chạy một số chuỗi song song trên một số thiết bị (giả sử 2 trên mỗi thiết bị). Đây hóa ra là một chương trình mà chúng ta chỉ có thể "lập bản đồ" trên các thiết bị, tức là một chương trình không cần tập thể. Để đảm bảo mỗi chương trình thực thi một chuỗi Markov khác nhau (trái ngược với việc chạy cùng một chuỗi), chúng tôi chuyển một giá trị khác cho hạt ngẫu nhiên vào mỗi thiết bị.
Hãy thử nó với một bài toán đồ chơi lấy mẫu từ phân phối Gaussian 2-D. Chúng tôi có thể sử dụng chức năng MCMC hiện có của TFP. Nói chung, chúng tôi cố gắng đưa hầu hết logic vào bên trong chức năng được ánh xạ của chúng tôi để phân biệt rõ ràng hơn giữa những gì đang chạy trên tất cả các thiết bị so với chỉ những gì đầu tiên.
def run(seed):
target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob
initial_state = jnp.zeros([2, 2]) # 2 chains
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
def trace_fn(state, pkr):
return target_log_prob(state)
states, log_prob = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
kernel=kernel,
current_state=initial_state,
trace_fn=trace_fn,
seed=seed
)
return states, log_prob
Bằng cách riêng của mình, run chức năng mất trong một hạt giống ngẫu nhiên không quốc tịch (để xem có bao stateless việc ngẫu nhiên, bạn có thể đọc TFP trên JAX máy tính xách tay hoặc xem hướng dẫn JAX 101 ). Lập bản đồ run qua hạt giống khác nhau sẽ cho kết quả trong việc điều hành một vài chuỗi Markov độc lập.
states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)
(8, 1000, 2, 2) (8, 1000, 2)
Lưu ý cách bây giờ chúng ta có một trục phụ tương ứng với mỗi thiết bị. Chúng ta có thể sắp xếp lại các kích thước và làm phẳng chúng để lấy trục cho 16 chuỗi.
states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()
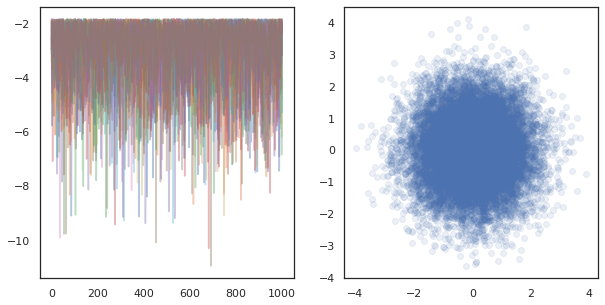
Khi chạy chuỗi độc lập trên nhiều thiết bị, đó là dễ dàng như pmap -ing qua một hàm sử dụng tfp.mcmc , đảm bảo chúng tôi vượt qua những giá trị khác nhau cho các hạt giống ngẫu nhiên cho mỗi thiết bị.
Làm sắc nét dữ liệu
Khi chúng tôi thực hiện MCMC, phân phối đích thường là phân phối sau thu được bằng cách điều hòa trên tập dữ liệu và việc tính toán mật độ log chưa chuẩn hóa liên quan đến việc tổng hợp khả năng xảy ra cho mỗi dữ liệu được quan sát.
Với bộ dữ liệu rất lớn, việc chạy một chuỗi trên một thiết bị có thể rất tốn kém. Tuy nhiên, khi chúng tôi có quyền truy cập vào nhiều thiết bị, chúng tôi có thể chia nhỏ tập dữ liệu trên các thiết bị để tận dụng tốt hơn máy tính mà chúng tôi có sẵn.
Nếu chúng ta muốn làm MCMC với một tập dữ liệu sharded, chúng ta cần phải đảm bảo unnormalized log-mật độ chúng ta tính toán trên mỗi thiết bị đại diện cho tổng, tức là mật độ trên tất cả dữ liệu, nếu không mỗi thiết bị sẽ được làm MCMC với mục tiêu không chính xác của mình phân bổ. Để kết thúc này, TFP hiện nay có các công cụ mới (tức là tfp.experimental.distribute và tfp.experimental.mcmc ) cho phép tính toán "sharded" xác suất log và làm MCMC với họ.
Các bản phân phối được chia nhỏ
Cốt lõi trừu tượng TFP hiện nay cung cấp cho máy tính probabiliities log sharded là Sharded meta-phân phối, trong đó có một bản phân phối như là đầu vào và trả về một bản phân phối mới có tính chất cụ thể khi thực hiện trong một bối cảnh SPMD. Sharded cuộc sống trong tfp.experimental.distribute .
Bằng trực giác, một Sharded tương ứng với phân phối cho một tập hợp các biến ngẫu nhiên đã được "chia" giữa các thiết bị. Trên mỗi thiết bị, họ sẽ tạo ra các mẫu khác nhau và có thể có mật độ log khác nhau. Ngoài ra, một Sharded tương ứng với phân phối cho một "tấm" trong mô hình cách nói đồ họa, nơi mà các kích thước tấm là số lượng thiết bị.
Lấy mẫu một Sharded phân phối
Nếu chúng ta lấy mẫu từ một Normal phân bố trong một chương trình phúc pmap -ed sử dụng hạt giống trên mỗi thiết bị, chúng tôi sẽ nhận được cùng một mẫu trên mỗi thiết bị. Chúng ta có thể coi chức năng sau là lấy mẫu một biến ngẫu nhiên duy nhất được đồng bộ hóa trên các thiết bị.
# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32)
Nếu chúng ta quấn tfd.Normal(0., 1.) với một tfed.Sharded , chúng tôi một cách logic nay có tám biến ngẫu nhiên khác nhau (một trên mỗi thiết bị) và do đó sẽ tạo ra một mẫu khác nhau cho mỗi người, mặc dù đi qua trong hạt giống .
def f(seed, _):
return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([ 1.2152631 , 0.7818249 , 0.32549605, 0.6828047 ,
1.3973192 , -0.57830244, 0.37862757, 2.7706041 ], dtype=float32)
Một biểu diễn tương đương của phân bố này trên một thiết bị chỉ là 8 mẫu chuẩn độc lập. Mặc dù giá trị của mẫu sẽ khác nhau ( tfed.Sharded làm giả ngẫu nhiên hệ số hơi khác nhau), cả hai đều đại diện cho cùng một phân phối.
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))
DeviceArray([ 0.08086783, -0.38624594, -0.3756545 , 1.668957 ,
-1.2758069 , 2.1192007 , -0.85821325, 1.1305912 ], dtype=float32)
Tham gia các log-mật độ của một Sharded phân phối
Hãy xem điều gì sẽ xảy ra khi chúng tôi tính toán mật độ nhật ký của một mẫu từ phân phối thông thường trong ngữ cảnh SPMD.
def f(seed, _):
dist = tfd.Normal(0., 1.)
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32),
ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
-0.94012403, -0.94012403, -0.94012403, -0.94012403], dtype=float32))
Mỗi mẫu giống nhau trên mỗi thiết bị, vì vậy chúng tôi cũng tính toán mật độ giống nhau trên mỗi thiết bị. Theo trực giác, ở đây chúng ta chỉ có một phân phối trên một biến phân phối chuẩn duy nhất.
Với Sharded phân phối, chúng tôi có một phân phối trên 8 biến ngẫu nhiên, vì vậy khi chúng tôi tính toán log_prob của một mẫu, chúng tôi tổng hợp trên các thiết bị trên mỗi mật độ đăng nhập cá nhân. (Bạn có thể nhận thấy rằng tổng giá trị log_prob này lớn hơn giá trị log_prob singleton đã tính ở trên.)
def f(seed, _):
dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)
Sample: [ 1.2152631 0.7818249 0.32549605 0.6828047 1.3973192 -0.57830244 0.37862757 2.7706041 ] Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205]
Phân phối tương đương, "không cứng" tạo ra cùng một mật độ nhật ký.
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)
DeviceArray(-13.7349205, dtype=float32)
Một Sharded phân phối sản xuất giá trị khác nhau từ sample trên mỗi thiết bị, nhưng nhận được giá trị tương tự cho log_prob trên mỗi thiết bị. Chuyện gì đang xảy ra ở đây? Một Sharded phân phối hiện một psum trong nội bộ để đảm bảo log_prob giá trị là đồng bộ giữa các thiết bị. Tại sao chúng ta muốn hành vi này? Nếu chúng ta đang chạy chuỗi MCMC cùng trên mỗi thiết bị, chúng tôi muốn các target_log_prob là giống nhau trên mỗi thiết bị, ngay cả khi một số biến ngẫu nhiên trong việc tính toán được sharded giữa các thiết bị.
Thêm vào đó, một Sharded Đảm bảo phân phối gradient giữa các thiết bị là đúng, để đảm bảo rằng các thuật toán như HMC, trong đó có gradient của hàm log-mật độ như một phần của chức năng chuyển tiếp, tạo ra mẫu thích hợp.
Sharded JointDistribution s
Chúng ta có thể tạo ra các mô hình với nhiều Sharded biến ngẫu nhiên bằng cách sử dụng JointDistribution s (JDS). Thật không may, Sharded phân phối không thể được sử dụng một cách an toàn với vani tfd.JointDistribution s, nhưng tfp.experimental.distribute xuất khẩu "vá" JDS sẽ cư xử như Sharded phân phối.
def f(seed, _):
dist = tfed.JointDistributionSequential([
tfd.Normal(0., 1.),
tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
])
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
1.6121525, 1.6121525, 1.6121525], dtype=float32),
ShardedDeviceArray([ 0.8690128 , -0.83167845, 1.2209264 , 0.88412696,
0.76478404, -0.66208494, -0.0129658 , 0.7391483 ], dtype=float32)],
ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
-12.214451, -12.214451, -12.214451, -12.214451], dtype=float32))
Những JDS sharded thể có cả hai Sharded và vani TFP phân phối như các thành phần. Đối với các bản phân phối không cứng, chúng tôi nhận được cùng một mẫu trên mỗi thiết bị và đối với các bản phân phối được chia nhỏ, chúng tôi nhận được các mẫu khác nhau. Các log_prob trên mỗi thiết bị được đồng bộ là tốt.
MCMC với Sharded phân phối
Làm thế nào để chúng ta suy nghĩ về Sharded phân phối trong bối cảnh MCMC? Nếu chúng ta có một mô hình sinh sản có thể được diễn tả như một JointDistribution , chúng ta có thể chọn một số trục của mô hình đó để "mảnh vỡ" trên. Thông thường, một biến ngẫu nhiên trong mô hình sẽ tương ứng với dữ liệu được quan sát và nếu chúng tôi có một tập dữ liệu lớn mà chúng tôi muốn chia nhỏ trên các thiết bị, chúng tôi cũng muốn các biến có liên quan đến điểm dữ liệu cũng được chia nhỏ. Chúng tôi cũng có thể có các biến ngẫu nhiên "cục bộ" là một đối một với các quan sát mà chúng tôi đang phân tích, vì vậy chúng tôi sẽ phải chia nhỏ các biến ngẫu nhiên đó.
Chúng tôi sẽ đi qua những ví dụ về việc sử dụng Sharded phân phối với TFP MCMC trong phần này. Chúng tôi sẽ bắt đầu với một Bayesian dụ hồi quy logistic đơn giản hơn, và kết thúc bằng một ví dụ ma trận nhân tử, với mục tiêu chứng minh một số trường hợp sử dụng cho distribute thư viện.
Ví dụ: Hồi quy logistic Bayes cho MNIST
Chúng tôi muốn thực hiện hồi quy logistic Bayes trên một tập dữ liệu lớn; mô hình có trước \(p(\theta)\) so với trọng lượng hồi quy, và một khả năng \(p(y_i | \theta, x_i)\) được tóm tắt trên tất cả dữ liệu \(\{x_i, y_i\}_{i = 1}^N\) để có được tổng mật độ log doanh. Nếu chúng ta Shard dữ liệu của chúng tôi, chúng tôi Shard các biến ngẫu nhiên quan sát \(x_i\) và \(y_i\) trong mô hình của chúng tôi.
Chúng tôi sử dụng mô hình hồi quy logistic Bayes sau đây để phân loại MNIST:
\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]
Hãy tải MNIST bằng Tập dữ liệu TensorFlow.
mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.
raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.
Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1... WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your local data directory. If you'd instead prefer to read directly from our public GCS bucket (recommended if you're running on GCP), you can instead pass `try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`. HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio… Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.
Chúng tôi có 60000 hình ảnh đào tạo nhưng hãy tận dụng 8 lõi có sẵn của chúng tôi và chia nó ra 8 cách. Chúng tôi sẽ sử dụng tiện dụng này shard chức năng tiện ích.
def shard_value(x):
x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices
shard = functools.partial(jax.tree_map, shard_value)
sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)
(8, 7500, 784) (8, 7500)
Trước khi tiếp tục, chúng ta hãy thảo luận nhanh về độ chính xác của TPU và tác động của nó đối với HMC. TPUs thực hiện phép nhân ma trận sử dụng thấp bfloat16 chính xác cho tốc độ. bfloat16 phép nhân ma trận thường đủ cho nhiều ứng dụng học tập sâu, nhưng khi sử dụng với HMC, chúng tôi đã thực nghiệm thấy độ chính xác thấp hơn có thể dẫn đến phân kỳ quỹ đạo, khiến bị từ chối. Chúng ta có thể sử dụng phép nhân ma trận có độ chính xác cao hơn với chi phí tính toán bổ sung.
Để tăng độ chính xác matmul của chúng tôi, chúng tôi có thể sử dụng jax.default_matmul_precision trang trí với "tensorfloat32" chính xác (đối với độ chính xác cao hơn chúng ta có thể sử dụng "float32" chính xác).
Hãy xác định tại chúng tôi run chức năng, mà sẽ mất trong một hạt giống ngẫu nhiên (mà sẽ giống nhau trên mỗi thiết bị) và một mảnh MNIST. Hàm sẽ thực hiện mô hình nói trên và sau đó chúng tôi sẽ sử dụng chức năng MCMC vani của TFP để chạy một chuỗi đơn lẻ. Chúng tôi đảm bảo để trang trí run với jax.default_matmul_precision trang trí để đảm bảo nhân ma trận được điều hành với độ chính xác cao hơn, mặc dù trong ví dụ cụ thể dưới đây, chúng ta chỉ cần cũng có thể sử dụng jnp.dot(images, w, precision=lax.Precision.HIGH) .
# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device.
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
images, labels = data # a sharded dataset
num_examples, dim = images.shape
num_classes = 10
def model_fn():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
logits = jnp.dot(images, w) + b
yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
shard_axis_name='data')
model = tfed.JointDistributionCoroutine(model_fn)
init_seed, sample_seed = random.split(seed)
initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`
def target_log_prob(*state):
return model.log_prob((*state, labels))
def accuracy(w, b):
logits = images.dot(w) + b
preds = logits.argmax(axis=-1)
# We take the average accuracy across devices by using `lax.pmean`
return lax.pmean((preds == labels).mean(), 'data')
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
def trace_fn(state, pkr):
return (
target_log_prob(*state),
accuracy(*state),
pkr.new_step_size)
states, trace = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
current_state=initial_state,
kernel=kernel,
trace_fn=trace_fn,
seed=sample_seed
)
return states, trace
jax.pmap bao gồm một biên dịch JIT nhưng chức năng biên soạn được lưu trữ sau khi cuộc gọi đầu tiên. Chúng tôi sẽ gọi run và bỏ qua những đầu ra để cache biên dịch.
%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)
CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s Wall time: 1min 54s
Bây giờ chúng ta sẽ gọi run lại để xem việc thực hiện thực tế phải mất bao lâu.
%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)
CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s Wall time: 1min 43s
Chúng tôi đang thực hiện 200.000 bước đi tắt đón đầu, mỗi bước tính toán một gradient trên toàn bộ tập dữ liệu. Tách phép tính trên 8 lõi cho phép chúng tôi tính toán tương đương 200.000 kỷ nguyên đào tạo trong khoảng 95 giây, khoảng 2.100 kỷ nguyên mỗi giây!
Hãy vẽ biểu đồ mật độ log của từng mẫu và độ chính xác của từng mẫu:
fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()
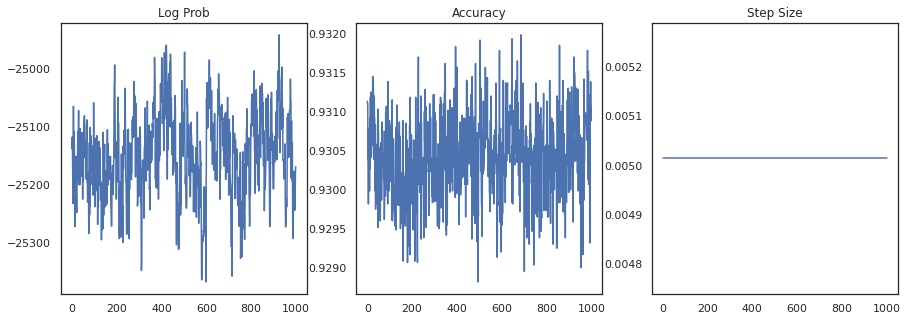
Nếu chúng tôi tập hợp các mẫu lại, chúng tôi có thể tính giá trị trung bình của mô hình Bayes để cải thiện hiệu suất của chúng tôi.
@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
images, labels = data
logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
probs = jax.nn.softmax(logits, axis=-1)
bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')
sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')
Average Accuracy: 0.9188529253005981 BMA Accuracy: 0.9264000058174133 Accuracy Improvement: 0.0075470805168151855
Mức trung bình của mô hình Bayes làm tăng độ chính xác của chúng tôi lên gần 1%!
Ví dụ: Hệ thống đề xuất MovieLens
Bây giờ chúng ta hãy thử suy luận với tập dữ liệu đề xuất MovieLens, là tập hợp những người dùng và xếp hạng của họ về các bộ phim khác nhau. Cụ thể, chúng ta có thể đại diện cho MovieLens như một \(N \times M\) ma trận đồng hồ \(W\) nơi \(N\) là số lượng người dùng và \(M\) là số phim; chúng tôi hy vọng \(N > M\). Các mục của \(W_{ij}\) là một boolean chỉ ra hay không sử dụng \(i\) xem phim \(j\). Lưu ý rằng MovieLens cung cấp xếp hạng của người dùng, nhưng chúng tôi đang bỏ qua chúng để đơn giản hóa vấn đề.
Đầu tiên, chúng tôi sẽ tải tập dữ liệu. Chúng tôi sẽ sử dụng phiên bản có 1 triệu lượt xếp hạng.
movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']
Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0... HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl… HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value=''))) Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value=''))) Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.
Chúng tôi sẽ làm một số tiền xử lý của bộ dữ liệu để có được ma trận đồng hồ \(W\).
raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']
movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])
num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1
movie_titles = dict(zip(movielens['train']['movie_id'],
movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]
watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)
(6040, 3706)
Chúng ta có thể xác định một mô hình sinh sản cho \(W\), sử dụng một mô hình thừa số ma trận xác suất đơn giản. Chúng tôi giả định một tiềm ẩn \(N \times D\) sử dụng ma trận \(U\) và tiềm ẩn \(M \times D\) ma trận phim \(V\), mà khi nhân sản xuất logits của một Bernoulli cho ma trận đồng hồ \(W\). Chúng tôi cũng sẽ bao gồm một vectơ thiên vị cho người dùng và phim ảnh, \(u\) và \(v\).
\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]
Đây là một ma trận khá lớn; 6040 người dùng và 3706 phim dẫn đến một ma trận với hơn 22 triệu mục trong đó. Làm cách nào để chúng ta tiếp cận với mô hình này? Vâng, nếu chúng ta giả định rằng \(N > M\) (tức là có nhiều người dùng hơn phim), sau đó nó sẽ làm cho tinh thần để Shard ma trận đồng hồ trên trục dùng, vì vậy mỗi thiết bị sẽ có một đoạn của ma trận đồng hồ tương ứng với một tập hợp con của người sử dụng . Không giống như các ví dụ trước, tuy nhiên, chúng tôi sẽ còn phải Shard lên \(U\) ma trận, vì nó có một nhúng cho mỗi người dùng, vì vậy mỗi thiết bị sẽ chịu trách nhiệm cho một mảnh \(U\) và một mảnh \(W\). Mặt khác, \(V\) sẽ unsharded và được đồng bộ hóa giữa các thiết bị.
sharded_watch_matrix = shard(watch_matrix)
Trước khi chúng tôi viết chúng tôi run , chúng ta hãy nhanh chóng thảo luận về những thách thức bổ sung với sharding địa phương biến ngẫu nhiên \(U\). Khi chạy HMC, vani tfp.mcmc.HamiltonianMonteCarlo kernel sẽ lấy mẫu xung lượng cho mỗi phần tử của nhà nước của chuỗi. Trước đây, chỉ các biến ngẫu nhiên không được tăng cường mới là một phần của trạng thái đó và thời điểm là giống nhau trên mỗi thiết bị. Khi bây giờ chúng tôi có một sharded \(U\), chúng ta cần phải lấy mẫu xung lượng khác nhau trên mỗi thiết bị cho \(U\), trong khi lấy mẫu xung lượng tương tự cho \(V\). Để thực hiện điều này, chúng ta có thể sử dụng tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo với một Sharded phân phối đà. Khi chúng tôi tiếp tục thực hiện tính toán song song hạng nhất, chúng tôi có thể đơn giản hóa điều này, ví dụ bằng cách lấy một chỉ báo phân đoạn cho hạt nhân HMC.
def make_run(*,
axis_name,
dim=20,
num_chains=2,
prior_variance=1.,
step_size=1e-2,
num_leapfrog_steps=100,
num_burnin_steps=1000,
num_results=500,
):
@functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
@jax.default_matmul_precision('tensorfloat32')
def run(key, watch_matrix):
num_users, num_movies = watch_matrix.shape
Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)
def prior_fn():
user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
return (user_embeddings, user_bias, movie_embeddings, movie_bias)
prior = tfed.JointDistributionCoroutine(prior_fn)
def model_fn():
user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
+ user_bias[..., :, None] + movie_bias[..., None, :])
yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
model = tfed.JointDistributionCoroutine(model_fn)
init_key, sample_key = random.split(key)
initial_state = prior.sample(seed=init_key, sample_shape=num_chains)
def target_log_prob(*state):
return model.log_prob((*state, watch_matrix))
momentum_distribution = tfed.JointDistributionSequential([
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
])
# We pass in momentum_distribution here to ensure that the momenta for
# user_embeddings and user_bias are also sharded
kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
num_leapfrog_steps,
momentum_distribution=momentum_distribution)
num_adaptation_steps = int(0.8 * num_burnin_steps)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)
def trace_fn(state, pkr):
return {
'log_prob': target_log_prob(*state),
'log_accept_ratio': pkr.inner_results.log_accept_ratio,
}
return tfm.sample_chain(
num_results, initial_state,
kernel=kernel,
num_burnin_steps=num_burnin_steps,
trace_fn=trace_fn,
seed=sample_key)
return run
Chúng tôi sẽ một lần nữa chạy nó một lần để bộ nhớ cache biên soạn run .
%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)
CPU times: user 56 s, sys: 1min 24s, total: 2min 20s Wall time: 3min 35s
Bây giờ chúng ta sẽ chạy lại nó mà không cần chi phí biên dịch.
%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)
CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s Wall time: 3min 1s
Có vẻ như chúng tôi đã hoàn thành khoảng 150.000 bước nhảy cóc trong khoảng 3 phút, vậy khoảng 83 bước nhảy cóc mỗi giây! Hãy vẽ biểu đồ tỷ lệ chấp nhận và mật độ nhật ký của các mẫu của chúng tôi.
fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
ax.plot(val[0]) # Indexing into a sharded array, each element is the same
ax.set_title(key);
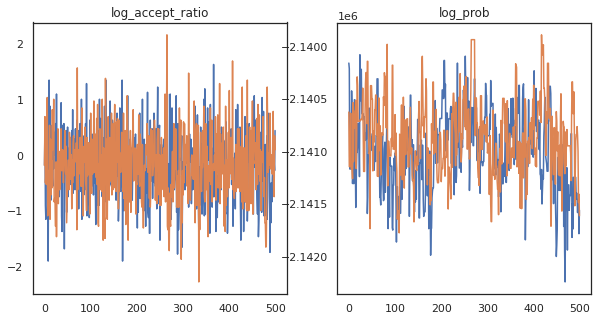
Bây giờ chúng tôi có một số mẫu từ chuỗi Markov của mình, hãy sử dụng chúng để đưa ra một số dự đoán. Đầu tiên, hãy giải nén từng thành phần. Hãy nhớ rằng user_embeddings và user_bias là chia trên thiết bị, vì vậy chúng ta cần phải nối chúng tôi ShardedArray để có được tất cả. Mặt khác, movie_embeddings và movie_bias đều giống nhau trên mọi thiết bị, vì vậy chúng tôi chỉ có thể chọn các giá trị từ các mảnh vỡ đầu tiên. Chúng tôi sẽ sử dụng thường xuyên numpy để sao chép các giá trị từ các TPUs trở lại CPU.
user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')
User embeddings: (500, 2, 6040, 20) User bias: (500, 2, 6040) Movie embeddings: (500, 2, 3706, 20) Movie bias: (500, 2, 3706)
Hãy cố gắng xây dựng một hệ thống khuyến nghị đơn giản sử dụng độ không đảm bảo đo được thu thập trong các mẫu này. Đầu tiên chúng ta hãy viết một hàm xếp hạng phim theo xác suất xem.
@jax.jit
def recommend(sample, user_id):
user_embeddings, user_bias, movie_embeddings, movie_bias = sample
movie_logits = (
jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
+ user_bias[user_id] + movie_bias)
return movie_logits.argsort()[::-1]
Bây giờ chúng ta có thể viết một hàm lặp lại trên tất cả các mẫu và đối với mỗi mẫu, chọn bộ phim được xếp hạng cao nhất mà người dùng chưa xem. Sau đó, chúng tôi có thể xem số lượng tất cả các phim được đề xuất trên các mẫu.
def get_recommendations(user_id):
movie_ids = []
already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
for i in range(500):
for j in range(2):
sample = jax.tree_map(lambda x: x[i, j], samples)
ranking = recommend(sample, user_id)
for movie_id in ranking:
if int(movie_id) not in already_watched:
movie_ids.append(movie_id)
break
return movie_ids
def plot_recommendations(movie_ids, ax=None):
titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
ax = ax or plt.gca()
names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
ax.bar(names, counts)
ax.set_xticklabels(names, rotation=90)
Hãy lấy người dùng xem nhiều phim nhất so với người xem ít nhất.
user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])
2314 20
Chúng tôi hy vọng hệ thống của chúng tôi có sự chắc chắn thêm về user_most hơn user_least , cho rằng chúng ta có thêm thông tin về những gì sắp xếp của phim user_most có nhiều khả năng để xem.
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');
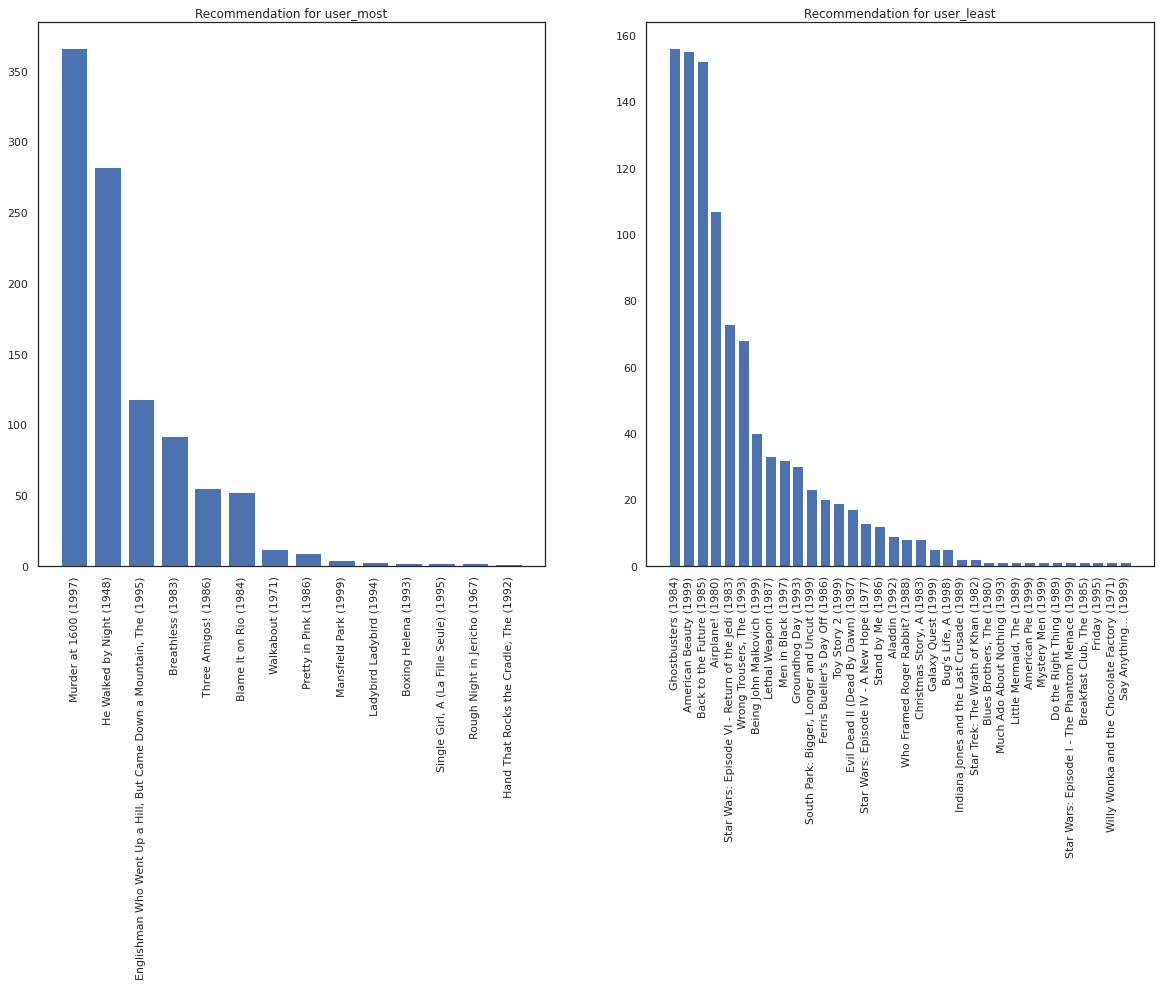
Chúng tôi thấy rằng có sai hơn trong các khuyến nghị của chúng tôi cho user_least phản ánh sự không chắc chắn khác của chúng tôi trong tùy chọn đồng hồ của họ.
Chúng ta cũng có thể xem các thể loại của các bộ phim được đề xuất.
most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');
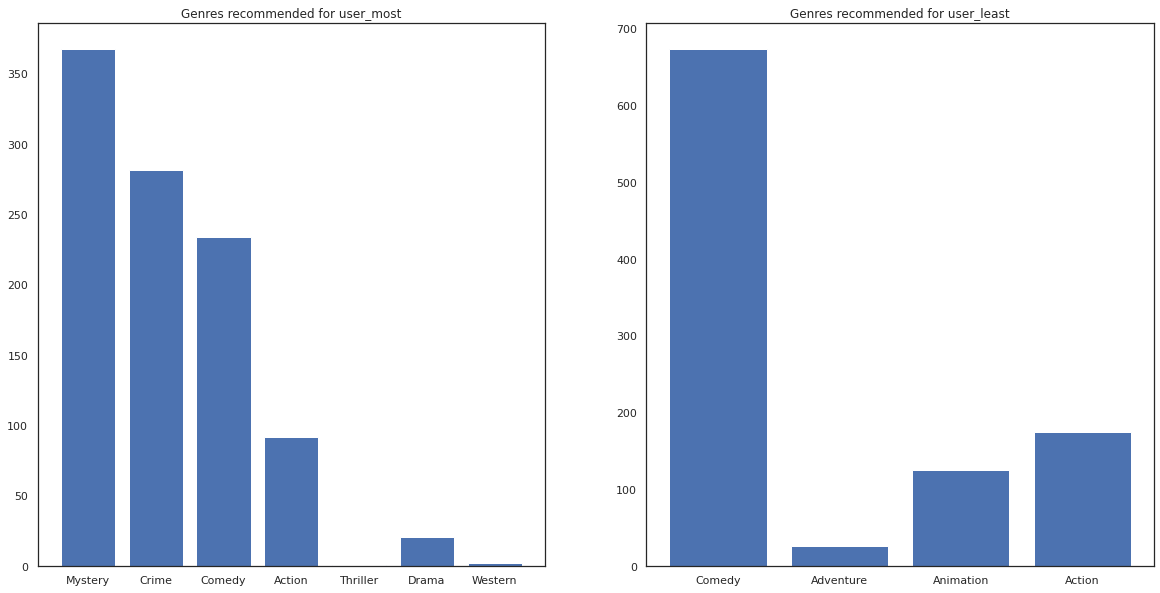
user_most đã chứng kiến rất nhiều phim và đã được khuyến cáo nhiều thể loại thích hợp như bí ẩn và tội phạm trong khi user_least chưa xem nhiều phim và đã được đề nghị nhiều phim chủ đạo, mà hài nghiêng và hành động.
