 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
JAX üzerindeki TensorFlow Probability (TFP) artık dağıtılmış sayısal hesaplama için araçlara sahiptir. Çok sayıda hızlandırıcıya ölçeklendirmek için araçlar, "tek programlı çoklu veri" paradigmasını veya kısaca SPMD'yi kullanarak kod yazma etrafında oluşturulmuştur.
Bu not defterinde, "SPMD'de nasıl düşünüleceğini" gözden geçireceğiz ve TPU bölmeleri veya GPU kümeleri gibi yapılandırmalara ölçeklendirme için yeni TFP soyutlamalarını tanıtacağız. Bu kodu kendiniz çalıştırıyorsanız, bir TPU çalışma zamanı seçtiğinizden emin olun.
Önce en son TFP, JAX ve TF sürümlerini yükleyeceğiz.
Yüklemeler
pip install jaxlib --upgrade -q 2>&1 1> /dev/nullpip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/nullpip install tf-nightly-cpu -q -I 2>&1 1> /dev/nullpip install jax -I -q --upgrade 2>&1 1>/dev/null
Bazı JAX yardımcı programları ile birlikte bazı genel kitaplıkları içe aktaracağız.
Kurulum ve İçe Aktarmalar
import functools
import collections
import contextlib
import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds
from tensorflow_probability.substrates import jax as tfp
sns.set(style='white')
INFO:tensorflow:Enabling eager execution INFO:tensorflow:Enabling v2 tensorshape INFO:tensorflow:Enabling resource variables INFO:tensorflow:Enabling tensor equality INFO:tensorflow:Enabling control flow v2
Ayrıca bazı kullanışlı TFP takma adları ayarlayacağız. Yeni soyutlamalar şu anda verilmektedir tfp.experimental.distribute ve tfp.experimental.mcmc .
tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc
Root = tfed.JointDistributionCoroutine.Root
Notebook'u bir TPU'ya bağlamak için JAX'ın aşağıdaki yardımcısını kullanıyoruz. Bağlandığımızı doğrulamak için, sekiz olması gereken cihaz sayısını yazdırıyoruz.
from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')
Found 8 devices
Hızlı bir giriş jax.pmap
TPU bağlandıktan sonra, sekiz cihazlara erişimi vardır. Ancak, JAX kodunu hevesle çalıştırdığımızda, JAX varsayılan olarak yalnızca bir tanesinde hesaplamaları çalıştırmaya başlar.
Birçok cihaz arasında bir hesaplama yürütmenin en basit yolu, her cihazın haritanın bir dizinini yürütmesini sağlayarak bir işlevi eşlemektir. JAX sağlar jax.pmap çeşitli cihazlar üzerinde işlevini eşleyen birine bir fonksiyon döner ( "paralel haritası") dönüşümü.
Aşağıdaki örnekte, 8 boyutunda bir dizi oluşturuyoruz (mevcut cihazların sayısıyla eşleşmesi için) ve buna 5 ekleyen bir işlevi eşliyoruz.
xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)
<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5. 6. 7. 8. 9. 10. 11. 12.]
Not biz almalarını ShardedDeviceArray çıktı dizisi fiziksel cihazlar arasında bölünmüş belirten tip geri.
jax.pmap semantik bir harita gibi davranır, ama onun davranışını değiştirmek birkaç önemli seçenek vardır. Varsayılan olarak, pmap işlevine tüm girişler üzerinde haritası çıkarılan varsayar, ancak bu davranışı değiştirebilirsiniz in_axes argüman.
xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)
[ 5. 6. 7. 8. 9. 10. 11. 12.]
Benzer şekilde, out_axes argüman pmap her cihazda değerler döndürmek için olup olmadığını belirler. Ayar out_axes için None otomatik 1 cihazda değer döndürür ve biz değerleri her cihazda aynı eminiz yalnızca kullanılmalıdır.
xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)
2.0
Yapmak istediğimiz şey, eşlenmiş bir saf işlev olarak kolayca ifade edilemezse ne olur? Örneğin, haritasını çıkardığımız eksen boyunca bir toplam yapmak istersek ne olur? JAX, daha ilginç ve karmaşık dağıtılmış programların yazılmasını sağlamak için cihazlar arasında iletişim kuran işlevler olan "kolektifler" sunar. Tam olarak nasıl çalıştıklarını anlamak için SPMD'yi tanıtacağız.
SPMD nedir?
Tek programlı çoklu veri (SPMD), cihazlar arasında aynı anda tek bir programın (yani aynı kodun) yürütüldüğü, ancak çalışan programların her birinin girdilerinin farklı olabileceği eşzamanlı bir programlama modelidir.
Program girişlerinden basit fonksiyonu (yani gibi bir şey ise x + 5 ) örneğinde yaptığımız gibi, SPMD bir program çalıştırarak sadece o farklı veri haritasını çıkarıyor jax.pmap erken. Ancak, bir işlevi "haritalamaktan" fazlasını yapabiliriz. JAX, cihazlar arasında iletişim kuran işlevler olan "kolektifler" sunar.
Örneğin, tüm cihazlarımızda bir miktarın toplamını almak isteyebiliriz. Bunu yapmadan önce, biz üzerinde Bizler eşleme ekseni bir ad atamanız gerekir pmap . Sonra kullanmak lax.psum biz üzerinde toplanmasıyla ediyoruz eksen biz adlandırılmış tespit sağlanması, cihazlar arasında bir miktar gerçekleştirmek için ( "paralel toplamı") fonksiyonu.
def f(x):
out = lax.psum(x, axis_name='i')
return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)
ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)
psum toplu agrega değerini x her aygıt ve harita üzerinde değeri yani senkronize out olduğu 28. Her cihazda. Artık basit bir "harita" gerçekleştirmiyoruz, ancak her bir cihazın hesaplamasının artık diğer cihazlarda aynı hesaplama ile kolektifler kullanarak sınırlı da olsa etkileşime girebildiği bir SPMD programı yürütüyoruz. Bu senaryoda, kullanabileceğimiz out_axes = None , çünkü psum değerini senkronize olacak.
def f(x):
out = lax.psum(x, axis_name='i')
return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))
ShardedDeviceArray(28., dtype=float32)
SPMD, aynı anda herhangi bir TPU konfigürasyonunda her cihazda çalışan bir program yazmamızı sağlar. 8 TPU çekirdeğinde makine öğrenimi yapmak için kullanılan kodun aynısı, yüzlerce ila binlerce çekirdeğe sahip olabilecek bir TPU bölmesinde kullanılabilir! Hakkında daha detaylı bir eğitim için jax.pmap ve SPMD, sen başvurabilirsiniz JAX 101 öğretici .
geniş ölçekte MCMC
Bu not defterinde, Bayes çıkarımı için Markov Zinciri Monte Carlo (MCMC) yöntemlerini kullanmaya odaklanıyoruz. MCMC için birçok cihazı kullanmamızın bir yolu olabilir, ancak bu not defterinde iki tanesine odaklanacağız:
- Farklı cihazlarda bağımsız Markov zincirleri çalıştırma. Bu durum oldukça basittir ve vanilya TFP ile yapmak mümkündür.
- Bir veri kümesini cihazlar arasında paylaşma. Bu durum biraz daha karmaşıktır ve yakın zamanda eklenen TFP makineleri gerektirir.
Bağımsız Zincirler
Diyelim ki MCMC kullanarak bir problem üzerinde Bayes çıkarımı yapmak istiyoruz ve birkaç zinciri paralel olarak birkaç cihazda çalıştırmak istiyoruz (her cihazda 2 diyelim). Bu, aygıtlar arasında yalnızca "eşleyebileceğimiz" bir program olduğu ortaya çıkıyor, yani kollektiflere ihtiyaç duymayan bir program. Her programın farklı bir Markov zinciri çalıştırdığından emin olmak için (aynı olanı çalıştırmak yerine), her cihaza rastgele tohum için farklı bir değer iletiyoruz.
Bunu bir 2-D Gauss dağılımından örneklemenin bir oyuncak problemi üzerinde deneyelim. TFP'nin mevcut MCMC işlevselliğini kutudan çıktığı gibi kullanabiliriz. Genel olarak, tüm cihazlarda çalışanla ilkini daha açık bir şekilde ayırt etmek için mantığın çoğunu haritalanmış işlevimizin içine koymaya çalışıyoruz.
def run(seed):
target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob
initial_state = jnp.zeros([2, 2]) # 2 chains
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
def trace_fn(state, pkr):
return target_log_prob(state)
states, log_prob = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
kernel=kernel,
current_state=initial_state,
trace_fn=trace_fn,
seed=seed
)
return states, log_prob
Kendi başına, run işlevi vatansız rasgele tohum alır (ne kadar vatansız rasgelelik iş görmek için, okuyabilir JAX üzerinde PFP'yi dizüstü ya bakınız JAX 101 öğretici ). Haritalama run farklı tohumlar üzerinde birçok bağımsız Markov zincirleri çalıştıran sonuçlanacaktır.
states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)
(8, 1000, 2, 2) (8, 1000, 2)
Artık her bir cihaza karşılık gelen ekstra bir eksenimiz olduğuna dikkat edin. 16 zincir için bir eksen elde etmek için boyutları yeniden düzenleyebilir ve düzleştirebiliriz.
states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()
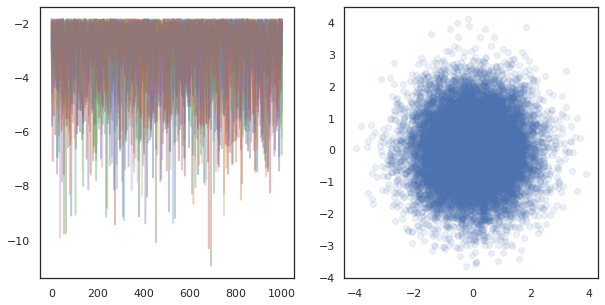
Birçok cihazda bağımsız zincirleri çalıştırırken olarak, bu kolay olarak var pmap kullandığı bir işlevi üzerinde -ing tfp.mcmc , sağlanması her cihaza rastgele tohum için farklı değerler geçmektedir.
Verileri parçalama
MCMC yaptığımızda, hedef dağılım genellikle bir veri kümesi üzerinde koşullandırma yoluyla elde edilen sonsal bir dağılımdır ve normalleştirilmemiş bir günlük yoğunluğunun hesaplanması, gözlemlenen her veri için olasılıkların toplanmasını içerir.
Çok büyük veri kümeleriyle, tek bir aygıtta bir zinciri çalıştırmak bile aşırı derecede pahalı olabilir. Bununla birlikte, birden fazla cihaza erişimimiz olduğunda, elimizdeki bilgi işlemden daha iyi yararlanmak için veri kümesini cihazlar arasında bölebiliriz.
Biz kanatlı bir veri kümesi ile MCMC yapmak isterseniz, biz başka türlü her cihaz kendi yanlış hedefle MCMC yapıyor olacak, biz her cihazda hesaplamak normalize edilmemiş günlük yoğunluklu yani tüm veriler üzerinde yoğunluk toplam temsil sağlamak için gereken dağıtım. Bu amaçla, TFP şimdi (yani yeni araçlara sahiptir tfp.experimental.distribute ve tfp.experimental.mcmc ) o bilgisayar "kanatlı bir" günlük olasılıklarını etkinleştirip onlarla MCMC yapıyor.
Parçalı dağıtımlar
Çekirdek soyutlama TFP hemen kanatlı bir günlük probabiliities olan işlem sağlar Sharded giriş olarak bir dağıtım alır ve bir SPMD bağlamında yürütüldüğünde spesifik özelliklere sahip olan yeni bir dağılımını verir meta dağılımı. Sharded yaşıyor tfp.experimental.distribute .
Sezgisel bir Sharded cihaz üzerinden "bölünmüş" olmuştur rasgele değişkenlerin bir dizi dağıtım karşılık gelir. Her cihazda farklı örnekler üretecekler ve ayrı ayrı farklı log yoğunluklarına sahip olabilirler. Seçenek olarak ise, bir Sharded plaka boyutu cihazların sayısı olan grafik modeli dilinde bir "levhası", dağıtım karşılık gelir.
Bir örnekleme Sharded dağılım
Biz dan örnek ise Normal bir program varlık dağıtım pmap her cihazda aynı tohum kullanılarak Ed, her cihazda aynı numuneyi alacak. Aşağıdaki işlevi, cihazlar arasında senkronize edilen tek bir rastgele değişkeni örneklemek olarak düşünebiliriz.
# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32)
Biz sarın Eğer tfd.Normal(0., 1.) bir ile tfed.Sharded biz mantıksal olarak şimdi (her cihazda bir) sekiz farklı rasgele değişkenler var ve bu nedenle aynı tohumdan geçen rağmen her biri için farklı bir örnek üretecek .
def f(seed, _):
return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([ 1.2152631 , 0.7818249 , 0.32549605, 0.6828047 ,
1.3973192 , -0.57830244, 0.37862757, 2.7706041 ], dtype=float32)
Bu dağılımın tek bir cihazda eşdeğer bir temsili sadece 8 bağımsız normal örnektir. Örneğin değeri (farklı olacaktır olsa tfed.Sharded biraz farklı bir yalancı rasgele sayı oluşturma yapar), aynı dağıtım temsil hem.
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))
DeviceArray([ 0.08086783, -0.38624594, -0.3756545 , 1.668957 ,
-1.2758069 , 2.1192007 , -0.85821325, 1.1305912 ], dtype=float32)
Bir log-yoğunluk alınması Sharded dağıtım
SPMD bağlamında normal bir dağıtımdan bir örneğin günlük yoğunluğunu hesapladığımızda ne olduğunu görelim.
def f(seed, _):
dist = tfd.Normal(0., 1.)
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32),
ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
-0.94012403, -0.94012403, -0.94012403, -0.94012403], dtype=float32))
Her örnek her cihazda aynıdır, bu nedenle her cihazda aynı yoğunluğu hesaplarız. Sezgisel olarak, burada yalnızca tek bir normal dağılımlı değişken üzerinde bir dağılıma sahibiz.
Bir ile Sharded dağılımı, biz hesaplamak nedenle zaman, 8 rastgele değişkenler üzerindeki dağılımı o log_prob bir numunenin, bireysel giriş yoğunluğu üzerinden her cihazlar arasında, toplar. (Bu toplam log_prob değerinin yukarıda hesaplanan singleton log_prob değerinden daha büyük olduğunu fark edebilirsiniz.)
def f(seed, _):
dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)
Sample: [ 1.2152631 0.7818249 0.32549605 0.6828047 1.3973192 -0.57830244 0.37862757 2.7706041 ] Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205]
Eşdeğer, "paylaşılmamış" dağıtım, aynı günlük yoğunluğunu üretir.
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)
DeviceArray(-13.7349205, dtype=float32)
Bir Sharded dağılımı farklı değerler üreten sample her bir cihaz, aynı için aynı değeri elde log_prob her cihazda. Burada neler oluyor? Bir Sharded dağılımı yapar psum sağlamak için içten log_prob değerleri cihazlar arasında senkronize bulunmaktadır. Bu davranışı neden isteyelim? Her cihazda aynı MCMC zincirini çalıştırıyorsanız, istediğimiz target_log_prob hesaplamasında bazı rasgele değişkenler cihazlar arasında kanatlı bir dahi, her cihaz için aynı olması.
Buna ek olarak, bir Sharded cihazlarda gradyanlar doğru olduğunu dağılımı sağlayan, geçiş işlevinin bir parçası olarak log-yoğunluk fonksiyonunun gradyanlar almak uygun örnekleri üretmek HMC gibi bu algoritmaları sağlamak.
Kanatlı bir JointDistribution s
Birden fazla olan modeller oluşturabilirsiniz Sharded kullanarak rastgele değişkenlerin JointDistribution ler (JDs). Ne yazık ki, Sharded dağılımlar güvenle vanilya ile kullanılamaz tfd.JointDistribution ler, ancak tfp.experimental.distribute ihracat gibi davranacaktır Jülyen "yamalı" Sharded dağılımları.
def f(seed, _):
dist = tfed.JointDistributionSequential([
tfd.Normal(0., 1.),
tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
])
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
1.6121525, 1.6121525, 1.6121525], dtype=float32),
ShardedDeviceArray([ 0.8690128 , -0.83167845, 1.2209264 , 0.88412696,
0.76478404, -0.66208494, -0.0129658 , 0.7391483 ], dtype=float32)],
ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
-12.214451, -12.214451, -12.214451, -12.214451], dtype=float32))
Bunlar kanatlı bir JDs ikisine de sahip olabilir Sharded bileşen olarak ve vanilyalı TFP dağılımları. Parçalanmamış dağılımlar için her cihazda aynı örneği, parçalı dağıtımlar için farklı örnekler elde ederiz. log_prob her cihazda de senkronize edilir.
İle MCMC Sharded dağılımları
Nasıl hakkında düşünüyorsunuz Sharded MCMC bağlamında dağılımları? Biz olarak ifade edilebilir bir üretken bir model varsa JointDistribution , karşımıza "kırığa" o modelin bazı eksenini alabilirsiniz. Tipik olarak, modeldeki bir rastgele değişken, gözlemlenen verilere karşılık gelir ve cihazlar arasında parçalamak istediğimiz büyük bir veri kümemiz varsa, veri noktalarıyla ilişkili değişkenlerin de paylaşılmasını isteriz. Ayrıca, parçaladığımız gözlemlerle bire bir olan "yerel" rastgele değişkenlere sahip olabiliriz, bu nedenle bu rastgele değişkenleri ek olarak parçalamamız gerekecek.
Biz kullanımının örneklerini ele alacağız Sharded bu bölümde TFP MCMC ile dağılımlar. Biz daha basit Bayes lojistik regresyon örnekle başlayalım ve bazı kullanım-örnekler de sergilemektedir hedefiyle, bir matris ayrıştırma örnekle bitireceğim distribute kütüphanesi.
Örnek: MNIST için Bayes lojistik regresyon
Büyük bir veri setinde Bayesian lojistik regresyon yapmak istiyoruz; Model, önceki sahip \(p(\theta)\) regresyon ağırlıkları üzerinde ve bir olabilirlik \(p(y_i | \theta, x_i)\) tüm veriler üzerinde toplanır \(\{x_i, y_i\}_{i = 1}^N\) total eklem günlük yoğunluğu elde edildi. Bizim veri shard, biz gözlenen rastgele değişkenler shard ediyorum \(x_i\) ve \(y_i\) bizim modelinde.
MNIST sınıflandırması için aşağıdaki Bayes lojistik regresyon modelini kullanıyoruz:
\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]
TensorFlow Veri Kümelerini kullanarak MNIST'i yükleyelim.
mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.
raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.
Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1... WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your local data directory. If you'd instead prefer to read directly from our public GCS bucket (recommended if you're running on GCP), you can instead pass `try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`. HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio… Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.
60000 eğitim görüntümüz var, ancak mevcut 8 çekirdeğimizden yararlanalım ve onu 8 yola ayıralım. Biz bu kullanışlı kullanacağız shard fayda fonksiyonu.
def shard_value(x):
x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices
shard = functools.partial(jax.tree_map, shard_value)
sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)
(8, 7500, 784) (8, 7500)
Devam etmeden önce, TPU'lardaki hassasiyeti ve bunun HMC üzerindeki etkisini hızlıca tartışalım. TPU düşük kullanılarak matris çarpımı çalıştırmak bfloat16 hızı hassas. bfloat16 matris çarpım genellikle çok derin öğrenme uygulamalar için yeterlidir, ancak HMC kullanıldığında, ampirik doğruluğu daha düşüktür rejeksiyonları neden yörüngeleri ayrılan yol açabilir bulduk. Bazı ek hesaplamalar pahasına daha yüksek hassasiyetli matris çarpımlarını kullanabiliriz.
Bizim matmul hassasiyetini artırmak için, kullanabileceğimiz jax.default_matmul_precision ile dekoratör "tensorfloat32" (hatta daha yüksek hassasiyet için yarar bir hassasiyetle "float32" kesinlik).
Şimdi bizim tanımlayalım run (her cihazda aynı olacaktır) rastgele tohumda alacak işlevi ve MNIST bir shard. İşlev, yukarıda belirtilen modeli uygulayacak ve ardından tek bir zinciri çalıştırmak için TFP'nin vanilya MCMC işlevselliğini kullanacağız. Emin süslemeleri için yapacağız run ile jax.default_matmul_precision aşağıda özel örnekte, sadece yanı kullanabilirsiniz olsa emin matris çarpım yüksek hassasiyetle çalışır hale getirmek için dekoratör jnp.dot(images, w, precision=lax.Precision.HIGH) .
# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device.
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
images, labels = data # a sharded dataset
num_examples, dim = images.shape
num_classes = 10
def model_fn():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
logits = jnp.dot(images, w) + b
yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
shard_axis_name='data')
model = tfed.JointDistributionCoroutine(model_fn)
init_seed, sample_seed = random.split(seed)
initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`
def target_log_prob(*state):
return model.log_prob((*state, labels))
def accuracy(w, b):
logits = images.dot(w) + b
preds = logits.argmax(axis=-1)
# We take the average accuracy across devices by using `lax.pmean`
return lax.pmean((preds == labels).mean(), 'data')
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
def trace_fn(state, pkr):
return (
target_log_prob(*state),
accuracy(*state),
pkr.new_step_size)
states, trace = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
current_state=initial_state,
kernel=kernel,
trace_fn=trace_fn,
seed=sample_seed
)
return states, trace
jax.pmap bir JIT derleme kapsar ancak derlenmiş işlev ilk çağrıdan sonra önbelleğe alınır. Biz arayacağım run ve derleme önbelleğe çıkışını görmezden.
%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)
CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s Wall time: 1min 54s
Şimdi çağrı edeceğiz run yine gerçek yürütme ne kadar sürdüğünü görmek için.
%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)
CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s Wall time: 1min 43s
Her biri tüm veri kümesi üzerinde bir gradyan hesaplayan 200.000 sıçrama adımı yürütüyoruz. Hesaplamayı 8 çekirdeğe bölmek, 200.000 eğitim dönemi eşdeğerini yaklaşık 95 saniyede, saniyede yaklaşık 2.100 dönem hesaplamamızı sağlar!
Her örneğin log yoğunluğunu ve her örneğin doğruluğunu çizelim:
fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()
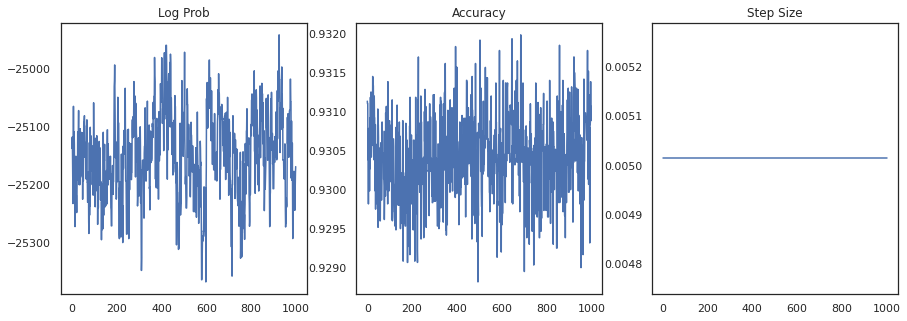
Örnekleri birleştirirsek, performansımızı iyileştirmek için bir Bayes modeli ortalamasını hesaplayabiliriz.
@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
images, labels = data
logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
probs = jax.nn.softmax(logits, axis=-1)
bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')
sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')
Average Accuracy: 0.9188529253005981 BMA Accuracy: 0.9264000058174133 Accuracy Improvement: 0.0075470805168151855
Bir Bayes modeli ortalaması, doğruluğumuzu neredeyse %1 oranında artırır!
Örnek: MovieLens öneri sistemi
Şimdi, kullanıcıların ve çeşitli filmlerin derecelendirmelerinin bir koleksiyonu olan MovieLens önerileri veri kümesiyle çıkarım yapmayı deneyelim. Özellikle, bir şekilde MovieLens temsil edebilir \(N \times M\) izle matris \(W\) \(N\) kullanıcıları ve sayısıdır \(M\) film sayısıdır; beklediğimiz \(N > M\). Girdileri \(W_{ij}\) kullanıcı olup olmadığını belirten bir boolean olan \(i\) film izlenmeye \(j\). MovieLens'in kullanıcı derecelendirmeleri sağladığını, ancak sorunu basitleştirmek için bunları göz ardı ettiğimizi unutmayın.
İlk önce veri setini yükleyeceğiz. 1 milyon reytingli versiyonu kullanacağız.
movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']
Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0... HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl… HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value=''))) Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value=''))) Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.
Biz seyretmek matrisi elde etmek veri kümesi bazı önişlemeyi yapacağım \(W\).
raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']
movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])
num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1
movie_titles = dict(zip(movielens['train']['movie_id'],
movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]
watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)
(6040, 3706)
Biz üretken bir modeli tanımlamak \(W\)basit bir olasılık matris ayrıştırma yöntemi kullanılarak. Biz gizli varsayalım \(N \times D\) kullanıcı matris \(U\) ve gizli \(M \times D\) film matris \(V\)izle matrisi için Bernoulli logits üretmek çarpılır, \(W\). Aynı zamanda, kullanıcı ve filmler için bir önyargı vektörleri ekleriz \(u\) ve \(v\).
\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]
Bu oldukça büyük bir matris; 6040 kullanıcı ve 3706 film, içinde 22 milyondan fazla giriş bulunan bir matrise yol açar. Bu modeli parçalamaya nasıl yaklaşırız? Eh, o varsayarsak \(N > M\) (filmlerinden daha kullanıcı var yani), o zaman her cihaz kullanıcılarının bir alt kümesine karşılık gelen izlemek matrisinin bir parça olurdu, böylece kullanıcı ekseni boyunca izle matrisi shard mantıklıdır . Önceki örneklerden farklı olarak, bununla birlikte, aynı zamanda yukarı shard gerekir \(U\) her kullanıcı için bir gömme sahip olduğu, her bir cihaz ile bir rastgele sorumlu olacak şekilde, matris \(U\) ve bir rastgele \(W\). Öte yandan, \(V\) unsharded olacak ve cihazlar arasında senkronize edilebilir.
sharded_watch_matrix = shard(watch_matrix)
Bizim yazmadan önce run , en hızlı yerel rasgele değişken Kırma işleminde ek zorlukları konuşalım \(U\). HMC, vanilya çalıştırırken tfp.mcmc.HamiltonianMonteCarlo zincir durumunun her bir eleman için, çekirdek örnek olacak momentumları. Önceden, yalnızca paylaşılmamış rastgele değişkenler bu durumun parçasıydı ve momentum her cihazda aynıydı. Şimdi bir kanatlı bir olduğunda \(U\)biz her cihaz üzerinde farklı momentumları örneklemek gerekir \(U\)aynı momentumları örneklerken, \(V\). Bunu gerçekleştirmek için, biz kullanabilirsiniz tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo bir ile Sharded ivme dağılımı. Paralel hesaplamayı birinci sınıf yapmaya devam ederken, örneğin HMC çekirdeğine bir parçalılık göstergesi alarak bunu basitleştirebiliriz.
def make_run(*,
axis_name,
dim=20,
num_chains=2,
prior_variance=1.,
step_size=1e-2,
num_leapfrog_steps=100,
num_burnin_steps=1000,
num_results=500,
):
@functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
@jax.default_matmul_precision('tensorfloat32')
def run(key, watch_matrix):
num_users, num_movies = watch_matrix.shape
Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)
def prior_fn():
user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
return (user_embeddings, user_bias, movie_embeddings, movie_bias)
prior = tfed.JointDistributionCoroutine(prior_fn)
def model_fn():
user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
+ user_bias[..., :, None] + movie_bias[..., None, :])
yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
model = tfed.JointDistributionCoroutine(model_fn)
init_key, sample_key = random.split(key)
initial_state = prior.sample(seed=init_key, sample_shape=num_chains)
def target_log_prob(*state):
return model.log_prob((*state, watch_matrix))
momentum_distribution = tfed.JointDistributionSequential([
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
])
# We pass in momentum_distribution here to ensure that the momenta for
# user_embeddings and user_bias are also sharded
kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
num_leapfrog_steps,
momentum_distribution=momentum_distribution)
num_adaptation_steps = int(0.8 * num_burnin_steps)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)
def trace_fn(state, pkr):
return {
'log_prob': target_log_prob(*state),
'log_accept_ratio': pkr.inner_results.log_accept_ratio,
}
return tfm.sample_chain(
num_results, initial_state,
kernel=kernel,
num_burnin_steps=num_burnin_steps,
trace_fn=trace_fn,
seed=sample_key)
return run
Derlenmiş önbelleğe kez Tekrar kaçıyorum run .
%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)
CPU times: user 56 s, sys: 1min 24s, total: 2min 20s Wall time: 3min 35s
Şimdi derleme yükü olmadan tekrar çalıştıracağız.
%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)
CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s Wall time: 3min 1s
Görünüşe göre yaklaşık 3 dakikada yaklaşık 150.000 birdirme adımı tamamladık, yani saniyede yaklaşık 83 sıçrayış adımı! Örneklerimizin kabul oranını ve log yoğunluğunu çizelim.
fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
ax.plot(val[0]) # Indexing into a sharded array, each element is the same
ax.set_title(key);
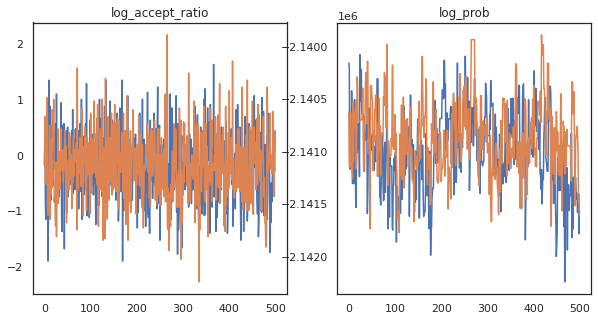
Artık Markov zincirimizden bazı örneklere sahip olduğumuza göre, bunları bazı tahminlerde bulunmak için kullanalım. İlk önce, bileşenlerin her birini çıkaralım. Unutmayın user_embeddings ve user_bias bizim bitiştirmek gerekir, böylece cihazın karşısında bölünmüş olan ShardedArray hepsini elde etmek. Öte yandan, movie_embeddings ve movie_bias her cihazda aynı, bu yüzden sadece ilk kırığın değeri alabilirsiniz. Biz normal kullanacağız numpy CPU'ya TPU arkasından değerleri kopyalamak için.
user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')
User embeddings: (500, 2, 6040, 20) User bias: (500, 2, 6040) Movie embeddings: (500, 2, 3706, 20) Movie bias: (500, 2, 3706)
Bu örneklerde yakalanan belirsizliği kullanan basit bir öneri sistemi oluşturmaya çalışalım. Önce filmleri izlenme olasılığına göre sıralayan bir fonksiyon yazalım.
@jax.jit
def recommend(sample, user_id):
user_embeddings, user_bias, movie_embeddings, movie_bias = sample
movie_logits = (
jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
+ user_bias[user_id] + movie_bias)
return movie_logits.argsort()[::-1]
Artık tüm örnekler üzerinde dolaşan ve her biri için kullanıcının daha önce izlemediği en üst sıradaki filmi seçen bir fonksiyon yazabiliriz. Daha sonra örnekler arasında önerilen tüm filmlerin sayısını görebiliriz.
def get_recommendations(user_id):
movie_ids = []
already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
for i in range(500):
for j in range(2):
sample = jax.tree_map(lambda x: x[i, j], samples)
ranking = recommend(sample, user_id)
for movie_id in ranking:
if int(movie_id) not in already_watched:
movie_ids.append(movie_id)
break
return movie_ids
def plot_recommendations(movie_ids, ax=None):
titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
ax = ax or plt.gca()
names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
ax.bar(names, counts)
ax.set_xticklabels(names, rotation=90)
En çok film izleyen kullanıcıyı en az izleyen kullanıcıya karşı alalım.
user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])
2314 20
Biz sistemimiz hakkında daha fazla kesinlik vardır umut user_most daha user_least biz filmlerin sıralar ilgili daha fazla bilgiye sahip olduğu göz önüne alındığında, user_most izlemek için daha olasıdır.
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');
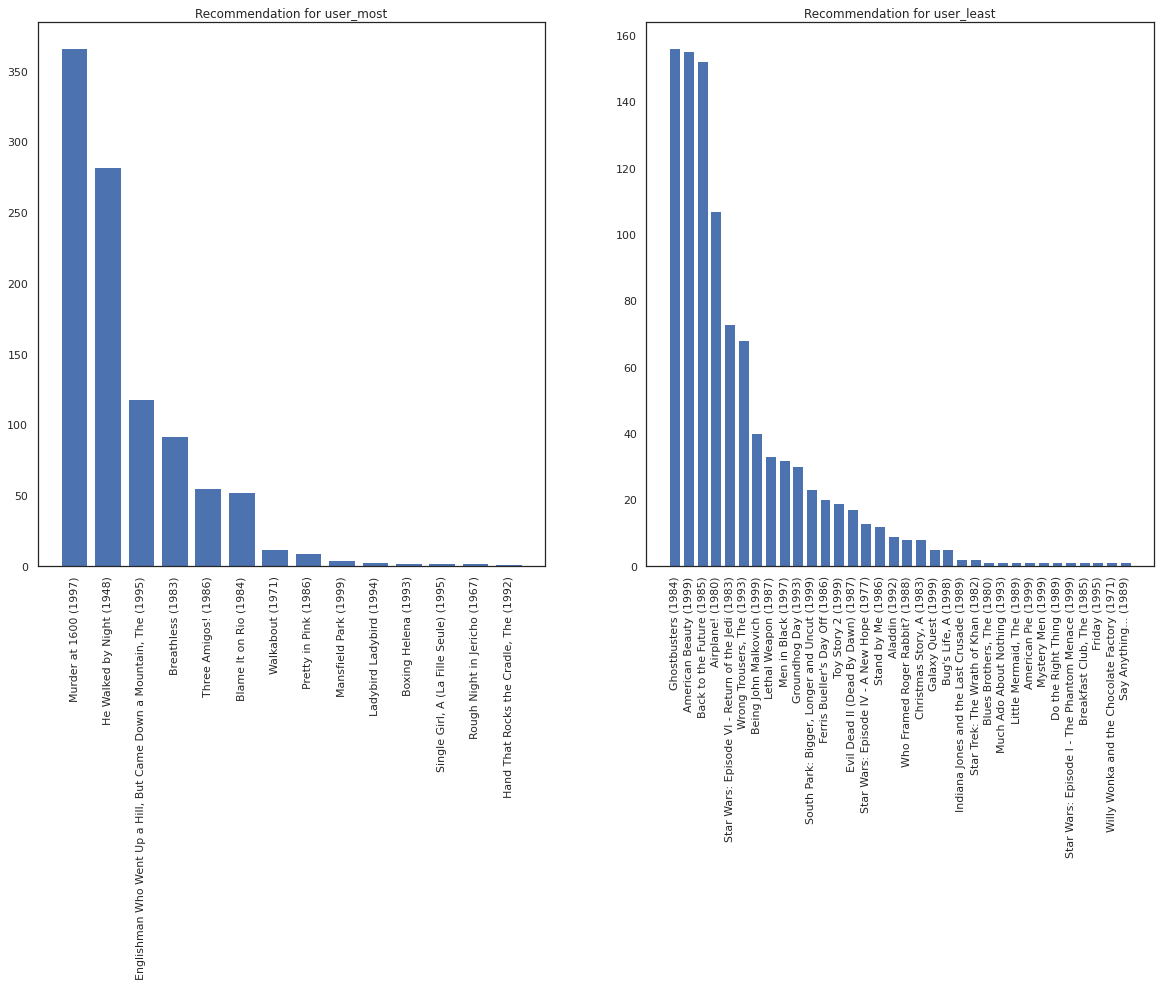
Biz sunduğumuz önerilerin daha varyans olduğunu görmek user_least onların izle tercihleri bölümünden ek belirsizliği yansıtmaktadır.
Ayrıca önerilen filmlerin türlerine de bakabiliriz.
most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');
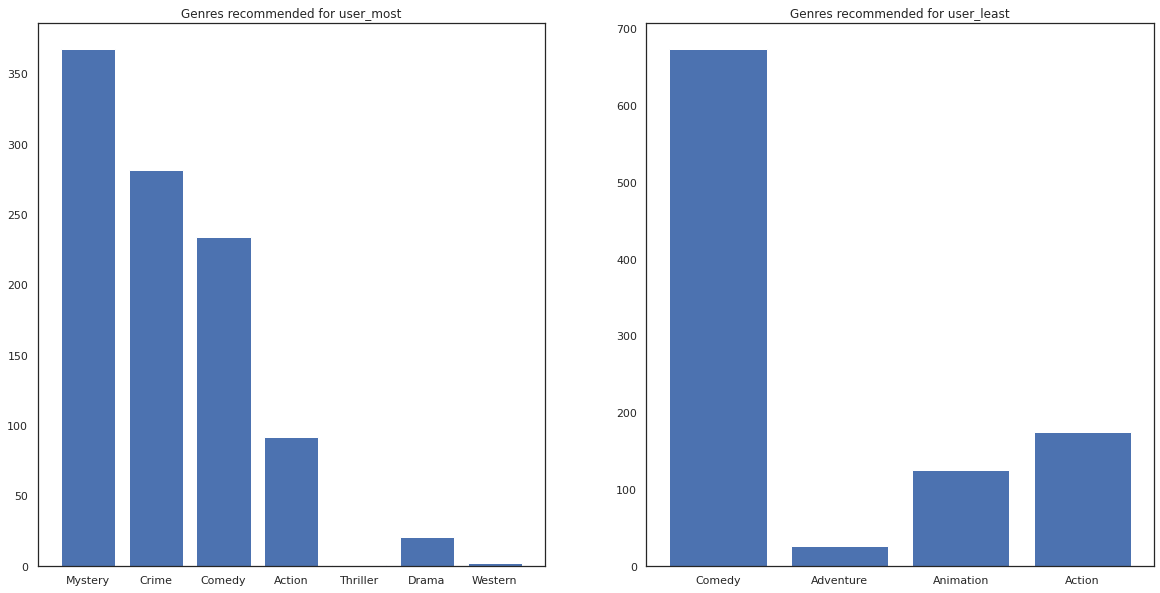
user_most bir sürü film gördü ve buna karşın gizem ve suç gibi daha niş türler tavsiye edilmiştir user_least çok film izledim değil ve hangi çarpık komedi ve aksiyon daha ana akım sinema, önerildi.
