 ดูบน TensorFlow.org ดูบน TensorFlow.org |  ทำงานใน Google Colab ทำงานใน Google Colab |  ดูแหล่งที่มาบน GitHub ดูแหล่งที่มาบน GitHub |  ดาวน์โหลดโน๊ตบุ๊ค ดาวน์โหลดโน๊ตบุ๊ค |
TensorFlow Probability (TFP) บน JAX มีเครื่องมือสำหรับการคำนวณเชิงตัวเลขแบบกระจายแล้ว ในการปรับขนาดให้เป็นตัวเร่งความเร็วจำนวนมาก เครื่องมือนี้สร้างขึ้นจากการเขียนโค้ดโดยใช้กระบวนทัศน์ "โปรแกรมเดียวหลายข้อมูล" หรือ SPMD โดยย่อ
ในโน้ตบุ๊กนี้ เราจะพูดถึงวิธี "คิดใน SPMD" และแนะนำ TFP abstractions ใหม่สำหรับการปรับขนาดการกำหนดค่าต่างๆ เช่น TPU pods หรือคลัสเตอร์ของ GPU หากคุณกำลังรันโค้ดนี้ด้วยตัวเอง ให้เลือกรันไทม์ TPU
ก่อนอื่นเราจะติดตั้ง TFP, JAX และ TF เวอร์ชันล่าสุด
การติดตั้ง
pip install jaxlib --upgrade -q 2>&1 1> /dev/nullpip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/nullpip install tf-nightly-cpu -q -I 2>&1 1> /dev/nullpip install jax -I -q --upgrade 2>&1 1>/dev/null
เราจะนำเข้าไลบรารีทั่วไปบางส่วน พร้อมด้วยยูทิลิตี้ JAX บางส่วน
ตั้งค่าและนำเข้า
import functools
import collections
import contextlib
import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds
from tensorflow_probability.substrates import jax as tfp
sns.set(style='white')
INFO:tensorflow:Enabling eager execution INFO:tensorflow:Enabling v2 tensorshape INFO:tensorflow:Enabling resource variables INFO:tensorflow:Enabling tensor equality INFO:tensorflow:Enabling control flow v2
เราจะสร้างนามแฝง TFP ที่มีประโยชน์ด้วย แนวคิดใหม่ที่มีให้ในปัจจุบัน tfp.experimental.distribute และ tfp.experimental.mcmc
tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc
Root = tfed.JointDistributionCoroutine.Root
ในการเชื่อมต่อโน้ตบุ๊กกับ TPU เราใช้ตัวช่วยต่อไปนี้จาก JAX เพื่อยืนยันว่าเราเชื่อมต่อแล้ว เราพิมพ์จำนวนอุปกรณ์ซึ่งควรเป็นแปดเครื่อง
from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')
Found 8 devices
แนะนำที่รวดเร็วในการ jax.pmap
หลังจากเชื่อมต่อ TPU เรามีการเข้าถึงแปดอุปกรณ์ อย่างไรก็ตาม เมื่อเรารันโค้ด JAX อย่างกระตือรือร้น JAX จะเรียกใช้การคำนวณโดยใช้ค่าเริ่มต้นเพียงโค้ดเดียว
วิธีที่ง่ายที่สุดในการดำเนินการคำนวณจากอุปกรณ์จำนวนมากคือการแมปฟังก์ชัน โดยให้อุปกรณ์แต่ละเครื่องดำเนินการดัชนีหนึ่งรายการของแผนที่ JAX ให้ jax.pmap ( "แผนที่ขนาน") การเปลี่ยนแปลงซึ่งจะเปลี่ยนฟังก์ชั่นเป็นหนึ่งในที่แมฟังก์ชั่นในอุปกรณ์หลาย
ในตัวอย่างต่อไปนี้ เราสร้างอาร์เรย์ขนาด 8 (เพื่อให้ตรงกับจำนวนอุปกรณ์ที่มี) และจับคู่ฟังก์ชันที่รวม 5 เข้าด้วยกัน
xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)
<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5. 6. 7. 8. 9. 10. 11. 12.]
โปรดทราบว่าเราได้รับการ ShardedDeviceArray ประเภทกลับแสดงให้เห็นว่าการส่งออกอาร์เรย์จะแบ่งร่างกายในอุปกรณ์
jax.pmap ทำหน้าที่ความหมายเหมือนแผนที่ แต่มีตัวเลือกที่สำคัญไม่กี่ที่ปรับเปลี่ยนพฤติกรรมของมัน โดยค่าเริ่มต้น pmap ถือว่าปัจจัยการผลิตทุกฟังก์ชั่นที่ถูกแมปมากกว่า แต่เราสามารถปรับเปลี่ยนพฤติกรรมนี้กับ in_axes โต้แย้ง
xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)
[ 5. 6. 7. 8. 9. 10. 11. 12.]
Analogously ที่ out_axes อาร์กิวเมนต์ pmap กำหนดหรือไม่ที่จะคืนค่าบนอุปกรณ์ทุก การตั้งค่า out_axes จะ None โดยอัตโนมัติส่งกลับค่าบนอุปกรณ์ที่ 1 และควรจะใช้เฉพาะในกรณีที่เรามีความมั่นใจค่าที่จะเหมือนกันในทุกอุปกรณ์
xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)
2.0
จะเกิดอะไรขึ้นเมื่อสิ่งที่เราต้องการทำไม่สามารถแสดงเป็นฟังก์ชันบริสุทธิ์ที่แมปได้ง่ายๆ ตัวอย่างเช่น เกิดอะไรขึ้นถ้าเราต้องการหาผลรวมข้ามแกนที่เรากำลังโยงอยู่? JAX นำเสนอ "collectives" ซึ่งเป็นฟังก์ชันที่สื่อสารข้ามอุปกรณ์ เพื่อให้สามารถเขียนโปรแกรมแบบกระจายที่น่าสนใจและซับซ้อนยิ่งขึ้น เพื่อให้เข้าใจถึงวิธีการทำงานอย่างแท้จริง เราจะแนะนำ SPMD
SPMD คืออะไร?
โปรแกรมเดียวหลายข้อมูล (SPMD) เป็นรูปแบบการเขียนโปรแกรมที่เกิดขึ้นพร้อมกันซึ่งโปรแกรมเดียว (เช่นรหัสเดียวกัน) ถูกดำเนินการพร้อมกันในอุปกรณ์ต่างๆ แต่อินพุตของแต่ละโปรแกรมที่ทำงานอยู่อาจแตกต่างกัน
ถ้าโปรแกรมของเราเป็นงานง่ายของปัจจัยการผลิตของตน (เช่นบางอย่างเช่น x + 5 ) การเรียกใช้โปรแกรมใน SPMD เป็นเพียงการทำแผนที่มันมากกว่าข้อมูลที่แตกต่างกันเช่นที่เราทำกับ jax.pmap ก่อนหน้านี้ อย่างไรก็ตาม เราสามารถทำได้มากกว่าแค่ "ทำแผนที่" กับฟังก์ชัน JAX มี "collectives" ซึ่งเป็นฟังก์ชันที่สื่อสารระหว่างอุปกรณ์ต่างๆ
ตัวอย่างเช่น เราอาจต้องการนำผลรวมของปริมาณจากอุปกรณ์ทั้งหมดของเรา ก่อนที่เราจะทำอย่างนั้นเราจำเป็นต้องกำหนดชื่อให้กับแกนที่เราทำแผนที่กำลังมากกว่าใน pmap จากนั้นเราจะใช้ lax.psum ( "ผลรวมขนาน") ฟังก์ชั่นในการดำเนินการรวมในอุปกรณ์เพื่อให้มั่นใจเราระบุชื่อแกนข้อสรุปที่เรากำลังมากกว่า
def f(x):
out = lax.psum(x, axis_name='i')
return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)
ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)
psum มวลรวมค่าของ x ในแต่ละอุปกรณ์และประสานความคุ้มค่าคุ้มทั่วแผนที่เช่น out เป็น 28. ในแต่ละอุปกรณ์ เราไม่ได้ดำเนินการ "แผนที่" แบบง่ายๆ อีกต่อไป แต่เรากำลังดำเนินการโปรแกรม SPMD ซึ่งขณะนี้การคำนวณของอุปกรณ์แต่ละเครื่องสามารถโต้ตอบกับการคำนวณแบบเดียวกันบนอุปกรณ์อื่นๆ ได้ แม้ว่าจะใช้วิธีที่จำกัดโดยใช้ส่วนรวม ในสถานการณ์นี้เราสามารถใช้ out_axes = None เพราะ psum จะประสานค่า
def f(x):
out = lax.psum(x, axis_name='i')
return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))
ShardedDeviceArray(28., dtype=float32)
SPMD ช่วยให้เราสามารถเขียนโปรแกรมหนึ่งโปรแกรมที่ทำงานบนอุปกรณ์ทุกเครื่องในการกำหนดค่า TPU ได้พร้อมกัน รหัสเดียวกันกับที่ใช้ทำการเรียนรู้ของเครื่องบนแกน TPU 8 คอร์ สามารถใช้กับพ็อด TPU ที่อาจมีคอร์นับแสนถึงหลายพัน! สำหรับการกวดวิชารายละเอียดเพิ่มเติมเกี่ยว jax.pmap และ SPMD คุณสามารถดูได้ที่ JAX 101 กวดวิชา
MCMC ในระดับ
ในสมุดบันทึกนี้ เราเน้นการใช้วิธี Markov Chain Monte Carlo (MCMC) สำหรับการอนุมานแบบเบย์ อาจมีวิธีที่เราใช้อุปกรณ์จำนวนมากสำหรับ MCMC แต่ในสมุดบันทึกนี้ เราจะเน้นที่สอง:
- ใช้งานเครือ Markov อิสระบนอุปกรณ์ต่างๆ กรณีนี้ค่อนข้างเรียบง่ายและสามารถทำได้ด้วย vanilla TFP
- การแชร์ชุดข้อมูลระหว่างอุปกรณ์ กรณีนี้ซับซ้อนกว่าเล็กน้อยและต้องใช้เครื่องจักร TFP ที่เพิ่มเข้ามาเมื่อเร็วๆ นี้
โซ่อิสระ
สมมติว่าเราต้องการอนุมานแบบเบย์เกี่ยวกับปัญหาโดยใช้ MCMC และต้องการเรียกใช้หลายกลุ่มพร้อมกันในอุปกรณ์หลายเครื่อง (เช่น 2 บนอุปกรณ์แต่ละเครื่อง) กลายเป็นโปรแกรมที่เราสามารถ "ทำแผนที่" ข้ามอุปกรณ์ได้ กล่าวคือ โปรแกรมที่ไม่ต้องมีส่วนรวม เพื่อให้แน่ใจว่าแต่ละโปรแกรมดำเนินการลูกโซ่ Markov ที่แตกต่างกัน (ซึ่งต่างจากการเรียกใช้โปรแกรมเดียวกัน) เราจึงส่งค่าที่ต่างกันสำหรับการสุ่มเมล็ดไปยังแต่ละอุปกรณ์
ลองใช้ปัญหาของเล่นสุ่มตัวอย่างจากการแจกแจงแบบเกาส์เซียน 2 มิติ เราสามารถใช้ฟังก์ชัน MCMC ที่มีอยู่ของ TFP ได้ทันที โดยทั่วไปแล้ว เราพยายามใส่ตรรกะส่วนใหญ่ในฟังก์ชันที่แมปของเราเพื่อแยกความแตกต่างระหว่างสิ่งที่ทำงานบนอุปกรณ์ทั้งหมดกับอุปกรณ์แรกให้ชัดเจนยิ่งขึ้น
def run(seed):
target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob
initial_state = jnp.zeros([2, 2]) # 2 chains
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
def trace_fn(state, pkr):
return target_log_prob(state)
states, log_prob = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
kernel=kernel,
current_state=initial_state,
trace_fn=trace_fn,
seed=seed
)
return states, log_prob
โดยตัวมันเองที่ run ฟังก์ชั่นใช้เวลาในไร้สัญชาติเมล็ดสุ่ม (เพื่อดูวิธีการทำงานไร้สัญชาติสุ่มคุณสามารถอ่าน TFP ใน JAX โน้ตบุ๊คหรือดู JAX 101 กวดวิชา ) การทำแผนที่ run มากกว่าเมล็ดพันธุ์ที่แตกต่างกันจะมีผลในการทำงานหลายโซ่มาร์คอฟเป็นอิสระ
states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)
(8, 1000, 2, 2) (8, 1000, 2)
สังเกตว่าตอนนี้เรามีแกนพิเศษที่สอดคล้องกับแต่ละอุปกรณ์ได้อย่างไร เราสามารถจัดเรียงขนาดใหม่และทำให้แบนราบได้เพื่อให้ได้แกนสำหรับโซ่ 16 อัน
states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()
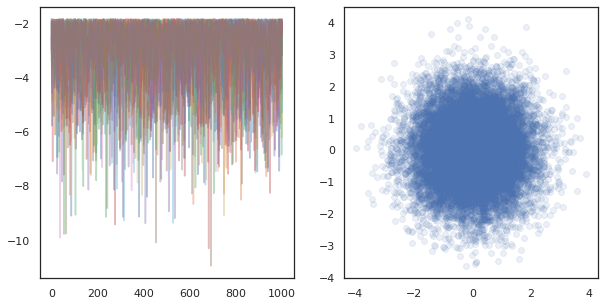
เมื่อใช้โซ่อิสระบนอุปกรณ์จำนวนมากก็เป็นเรื่องง่ายเหมือน pmap ไอเอ็นจีมากกว่าฟังก์ชั่นที่ใช้ tfp.mcmc เพื่อให้มั่นใจว่าเราส่งผ่านค่าที่แตกต่างกันสำหรับเมล็ดพันธุ์แบบสุ่มไปยังอุปกรณ์แต่ละตัว
การแบ่งข้อมูล
เมื่อเราทำ MCMC การกระจายเป้าหมายมักจะเป็นการแจกแจงภายหลังที่ได้รับจากการปรับสภาพบนชุดข้อมูล และการคำนวณความหนาแน่นของบันทึกที่ไม่เป็นไปตามมาตรฐานจะเกี่ยวข้องกับการรวมโอกาสที่เป็นไปได้สำหรับข้อมูลที่สังเกตแต่ละรายการ
ด้วยชุดข้อมูลที่มีขนาดใหญ่มาก อาจมีราคาแพงมากหากเรียกใช้โซ่เดียวบนอุปกรณ์เครื่องเดียว อย่างไรก็ตาม เมื่อเรามีสิทธิ์เข้าถึงอุปกรณ์หลายเครื่อง เราสามารถแยกชุดข้อมูลระหว่างอุปกรณ์ต่างๆ เพื่อใช้ประโยชน์จากการประมวลผลที่เรามีให้ได้ดียิ่งขึ้น
ถ้าเราต้องการที่จะทำ MCMC กับชุด sharded เราต้องให้แน่ใจว่าการเข้าสู่ระบบที่มีความหนาแน่น unnormalized เราคำนวณบนอุปกรณ์แต่ละหมายถึงทั้งหมดคือความหนาแน่นมากกว่าข้อมูลทั้งหมดมิฉะนั้นแต่ละอุปกรณ์จะทำ MCMC กับเป้าหมายที่ไม่ถูกต้องของตัวเอง การกระจาย. ด้วยเหตุนี้ TFP ตอนนี้มีเครื่องมือใหม่ ๆ (เช่น tfp.experimental.distribute และ tfp.experimental.mcmc ) ที่ช่วยให้การคำนวณ "sharded" ความน่าจะเป็นและการทำบันทึก MCMC กับพวกเขา
การกระจายแบบแบ่งส่วน
TFP หลักนามธรรมในขณะนี้ให้สำหรับการคำนวณ probabiliities บันทึก sharded เป็น Sharded meta-กระจายซึ่งจะมีการจัดจำหน่ายที่เป็น input และผลตอบแทนการจัดจำหน่ายใหม่ที่มีคุณสมบัติเฉพาะเมื่อดำเนินการในบริบท SPMD Sharded ชีวิตใน tfp.experimental.distribute
สังหรณ์ใจเป็น Sharded สอดคล้องแจกจ่ายให้กับชุดของตัวแปรสุ่มที่ได้รับการ "แยก" ในอุปกรณ์ ในแต่ละอุปกรณ์ พวกเขาจะผลิตตัวอย่างที่แตกต่างกัน และสามารถมีบันทึกความหนาแน่นต่างกันได้ ผลัดกัน Sharded สอดคล้องกับการกระจายไปยัง "จาน" ในรูปแบบกราฟิกการพูดจาที่ขนาดจานเป็นจำนวนของอุปกรณ์
การสุ่มตัวอย่าง Sharded กระจาย
ถ้าเราลิ้มลองจาก Normal การจัดจำหน่ายในโปรแกรมเป็น pmap -ed โดยใช้เมล็ดพันธุ์เดียวกันในแต่ละอุปกรณ์ที่เราจะได้รับตัวอย่างเดียวกันในแต่ละอุปกรณ์ เราสามารถนึกถึงฟังก์ชันต่อไปนี้เป็นการสุ่มตัวอย่างตัวแปรสุ่มตัวเดียวที่ซิงโครไนซ์ระหว่างอุปกรณ์ต่างๆ
# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32)
ถ้าเราตัด tfd.Normal(0., 1.) มี tfed.Sharded เรามีเหตุผลในขณะนี้มีแปดตัวแปรสุ่มที่แตกต่างกัน (หนึ่งในอุปกรณ์แต่ละคน) และดังนั้นจึงจะผลิตตัวอย่างที่แตกต่างกันสำหรับแต่ละคนแม้จะผ่านในเมล็ดเดียวกัน .
def f(seed, _):
return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([ 1.2152631 , 0.7818249 , 0.32549605, 0.6828047 ,
1.3973192 , -0.57830244, 0.37862757, 2.7706041 ], dtype=float32)
การแทนค่าที่เท่ากันของการกระจายนี้บนอุปกรณ์เครื่องเดียวเป็นเพียงตัวอย่างปกติที่เป็นอิสระ 8 ตัวอย่าง แม้ว่าค่าของกลุ่มตัวอย่างที่จะแตกต่างกัน ( tfed.Sharded ไม่สร้างเลขสุ่มหลอกแตกต่างกันเล็กน้อย) พวกเขาทั้งสองเป็นตัวแทนของการกระจายเดียวกัน
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))
DeviceArray([ 0.08086783, -0.38624594, -0.3756545 , 1.668957 ,
-1.2758069 , 2.1192007 , -0.85821325, 1.1305912 ], dtype=float32)
การบันทึกความหนาแน่นของ Sharded กระจาย
มาดูกันว่าจะเกิดอะไรขึ้นเมื่อเราคำนวณความหนาแน่นบันทึกของกลุ่มตัวอย่างจากการแจกแจงแบบปกติในบริบท SPMD
def f(seed, _):
dist = tfd.Normal(0., 1.)
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32),
ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
-0.94012403, -0.94012403, -0.94012403, -0.94012403], dtype=float32))
แต่ละตัวอย่างจะเหมือนกันในแต่ละอุปกรณ์ ดังนั้นเราจึงคำนวณความหนาแน่นเท่ากันในแต่ละอุปกรณ์ด้วย ตามสัญชาตญาณ เรามีการแจกแจงบนตัวแปรแบบกระจายปกติเพียงตัวเดียว
ด้วย Sharded กระจายเรามีการกระจายกว่า 8 ตัวแปรสุ่มดังนั้นเมื่อเราคำนวณ log_prob ของกลุ่มตัวอย่างที่เราสรุปในอุปกรณ์มากกว่าแต่ละหนาแน่นบันทึกของแต่ละบุคคล (คุณอาจสังเกตเห็นว่าค่า log_prob ทั้งหมดนี้มากกว่าค่า singleton log_prob ที่คำนวณไว้ด้านบน)
def f(seed, _):
dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)
Sample: [ 1.2152631 0.7818249 0.32549605 0.6828047 1.3973192 -0.57830244 0.37862757 2.7706041 ] Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205]
การกระจายแบบ "unsharded" ที่เทียบเท่ากันจะสร้างความหนาแน่นของบันทึกเดียวกัน
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)
DeviceArray(-13.7349205, dtype=float32)
Sharded กระจายผลิตค่าที่แตกต่างจาก sample ในอุปกรณ์แต่ละ แต่ได้รับค่าเหมือนกันสำหรับ log_prob ในแต่ละอุปกรณ์ เกิดอะไรขึ้นที่นี่? Sharded กระจายไม่ psum ภายในเพื่อให้แน่ใจว่าการ log_prob ค่าอยู่ในซิงค์ในอุปกรณ์ ทำไมเราต้องการพฤติกรรมนี้? ถ้าเรากำลังใช้โซ่ MCMC เดียวกันในแต่ละอุปกรณ์ที่เราต้องการให้ target_log_prob ที่จะเหมือนกันในแต่ละอุปกรณ์แม้ว่าบางตัวแปรสุ่มในการคำนวณจะ sharded ในอุปกรณ์
นอกจากนี้ Sharded กระจายเพื่อให้แน่ใจว่าการไล่ระดับสีในอุปกรณ์เป็นที่ถูกต้องเพื่อให้มั่นใจว่าอัลกอริทึมที่เหมือน HMC ซึ่งใช้การไล่ระดับสีของฟังก์ชั่นบันทึกความหนาแน่นเป็นส่วนหนึ่งของฟังก์ชั่นการเปลี่ยนแปลงผลิตตัวอย่างเหมาะสม
Sharded JointDistribution s
เราสามารถสร้างแบบจำลองที่มีหลาย Sharded ตัวแปรสุ่มโดยใช้ JointDistribution s (JDs) แต่น่าเสียดายที่ Sharded กระจายไม่สามารถใช้งานได้อย่างปลอดภัยด้วยวานิลลา tfd.JointDistribution s แต่ tfp.experimental.distribute การส่งออก "ปะ" JDs ที่จะทำตัวเหมือน Sharded กระจาย
def f(seed, _):
dist = tfed.JointDistributionSequential([
tfd.Normal(0., 1.),
tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
])
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
1.6121525, 1.6121525, 1.6121525], dtype=float32),
ShardedDeviceArray([ 0.8690128 , -0.83167845, 1.2209264 , 0.88412696,
0.76478404, -0.66208494, -0.0129658 , 0.7391483 ], dtype=float32)],
ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
-12.214451, -12.214451, -12.214451, -12.214451], dtype=float32))
JDs sharded เหล่านี้สามารถมีทั้ง Sharded และวานิลลา TFP กระจายเป็นส่วนประกอบ สำหรับการแจกแจงแบบแยกส่วน เราได้รับตัวอย่างเดียวกันในแต่ละอุปกรณ์ และสำหรับการแจกแจงแบบแบ่งส่วนข้อมูล เราจะได้ตัวอย่างที่แตกต่างกัน log_prob ในแต่ละอุปกรณ์จะตรงเช่นกัน
MCMC กับ Sharded กระจาย
ทำอย่างไรเราคิดเกี่ยวกับ Sharded กระจายในบริบทของ MCMC หรือไม่ ถ้าเรามีรูปแบบการกำเนิดที่สามารถแสดงเป็น JointDistribution เราสามารถเลือกแกนของรูปแบบที่บางอย่างเพื่อ "ชาร์ด" ข้าม โดยปกติ ตัวแปรสุ่มตัวหนึ่งในแบบจำลองจะสอดคล้องกับข้อมูลที่สังเกตได้ และหากเรามีชุดข้อมูลขนาดใหญ่ที่เราต้องการที่จะแบ่งส่วนข้อมูลในอุปกรณ์ต่างๆ เราก็ต้องการให้แบ่งส่วนข้อมูลตัวแปรที่เชื่อมโยงกับจุดข้อมูลด้วย นอกจากนี้เรายังอาจมีตัวแปรสุ่ม "ในเครื่อง" ที่เป็นหนึ่งต่อหนึ่งกับการสังเกตที่เรากำลังแบ่งส่วน ดังนั้นเราจะต้องแยกส่วนตัวแปรสุ่มเหล่านั้นเพิ่มเติม
เราจะไปกว่าตัวอย่างของการใช้งานของ Sharded กระจายกับ TFP MCMC ในส่วนนี้ เราจะเริ่มต้นด้วยการเป็นตัวอย่างที่ถดถอยโลจิสติคชกรรมง่ายและสรุปด้วยตัวอย่างเมทริกซ์ตีนเป็ดมีเป้าหมายในการแสดงให้เห็นถึงบางกรณีการใช้งานสำหรับการ distribute ห้องสมุด
ตัวอย่าง: การถดถอยโลจิสติกแบบเบย์สำหรับ MNIST
เราต้องการทำการถดถอยโลจิสติกแบบเบย์ในชุดข้อมูลขนาดใหญ่ แบบมีก่อน \(p(\theta)\) มากกว่าน้ำหนักการถดถอยและโอกาส \(p(y_i | \theta, x_i)\) ที่สรุปมากกว่าข้อมูลทั้งหมด \(\{x_i, y_i\}_{i = 1}^N\) ที่จะได้รับความหนาแน่นของการเข้าสู่ระบบทั้งหมดร่วมกัน ถ้าเรา Shard ข้อมูลของเราที่เราต้องการ Shard ตัวแปรสุ่มสังเกต \(x_i\) และ \(y_i\) ในรูปแบบของเรา
เราใช้แบบจำลองการถดถอยโลจิสติกแบบเบย์ต่อไปนี้สำหรับการจำแนกประเภท MNIST:
\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]
มาโหลด MNIST โดยใช้ชุดข้อมูล TensorFlow
mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.
raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.
Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1... WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your local data directory. If you'd instead prefer to read directly from our public GCS bucket (recommended if you're running on GCP), you can instead pass `try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`. HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio… Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.
เรามีอิมเมจการฝึกอบรม 60000 ภาพ แต่มาใช้ประโยชน์จากคอร์ที่มีอยู่ 8 คอร์ของเราและแยกออกเป็น 8 วิธี เราจะใช้นี้มีประโยชน์ shard ฟังก์ชั่นยูทิลิตี้
def shard_value(x):
x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices
shard = functools.partial(jax.tree_map, shard_value)
sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)
(8, 7500, 784) (8, 7500)
ก่อนที่เราจะดำเนินการต่อ มาพูดคุยกันอย่างรวดเร็วเกี่ยวกับความแม่นยำของ TPU และผลกระทบที่มีต่อ HMC TPUs ดำเนินการคูณเมทริกซ์โดยใช้ต่ำ bfloat16 แม่นยำสำหรับความเร็ว bfloat16 คูณเมทริกซ์มักจะเพียงพอสำหรับการใช้งานจำนวนมากเรียนรู้ลึก แต่เมื่อใช้กับ HMC เราได้สังเกตุพบว่ามีความแม่นยำต่ำสามารถนำไปสู่วิถีแยกทางที่ก่อให้เกิดการปฏิเสธ เราสามารถใช้การคูณเมทริกซ์ที่มีความแม่นยำสูงขึ้นได้ โดยต้องเสียค่าใช้จ่ายในการคำนวณเพิ่มเติม
เพื่อเพิ่มความแม่นยำ matmul ของเราเราสามารถใช้ jax.default_matmul_precision มัณฑนากรที่มี "tensorfloat32" ความแม่นยำ (เพื่อความแม่นยำที่สูงยิ่งขึ้นเราสามารถใช้ "float32" ความแม่นยำ)
ตอนนี้ขอให้เรากำหนด run ฟังก์ชั่นซึ่งจะใช้เวลาในเมล็ดสุ่ม (ซึ่งจะเหมือนกันในแต่ละอุปกรณ์) และเศษ MNIST ฟังก์ชันนี้จะนำโมเดลดังกล่าวไปใช้ และเราจะใช้ฟังก์ชัน vanilla MCMC ของ TFP เพื่อเรียกใช้เชนเดียว เราจะตรวจสอบให้แน่ใจในการตกแต่ง run กับ jax.default_matmul_precision มัณฑนากรเพื่อให้แน่ใจว่าการคูณเมทริกซ์จะทำงานที่มีความแม่นยำสูงขึ้นแม้ว่าในตัวอย่างโดยเฉพาะอย่างยิ่งด้านล่างเราก็เช่นกันสามารถใช้ jnp.dot(images, w, precision=lax.Precision.HIGH)
# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device.
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
images, labels = data # a sharded dataset
num_examples, dim = images.shape
num_classes = 10
def model_fn():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
logits = jnp.dot(images, w) + b
yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
shard_axis_name='data')
model = tfed.JointDistributionCoroutine(model_fn)
init_seed, sample_seed = random.split(seed)
initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`
def target_log_prob(*state):
return model.log_prob((*state, labels))
def accuracy(w, b):
logits = images.dot(w) + b
preds = logits.argmax(axis=-1)
# We take the average accuracy across devices by using `lax.pmean`
return lax.pmean((preds == labels).mean(), 'data')
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
def trace_fn(state, pkr):
return (
target_log_prob(*state),
accuracy(*state),
pkr.new_step_size)
states, trace = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
current_state=initial_state,
kernel=kernel,
trace_fn=trace_fn,
seed=sample_seed
)
return states, trace
jax.pmap รวมถึงการรวบรวม JIT แต่ฟังก์ชั่นที่รวบรวมอยู่ในแคชหลังจากที่สายแรก เราจะเรียก run และไม่สนใจออกไปยังแคชรวบรวม
%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)
CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s Wall time: 1min 54s
ตอนนี้เราจะเรียก run อีกครั้งเพื่อดูว่าระยะเวลาการดำเนินการที่เกิดขึ้นจริงจะใช้เวลา
%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)
CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s Wall time: 1min 43s
เรากำลังดำเนินการ 200,000 ก้าวกระโดด ซึ่งแต่ละขั้นตอนจะคำนวณการไล่ระดับบนชุดข้อมูลทั้งหมด การแยกการคำนวณออกเป็น 8 คอร์ช่วยให้เราสามารถคำนวณการฝึกอบรมที่เทียบเท่ากับ 200,000 ยุคในเวลาประมาณ 95 วินาที หรือประมาณ 2,100 ยุคต่อวินาที!
มาพลอตความหนาแน่นบันทึกของแต่ละตัวอย่างและความแม่นยำของตัวอย่างกัน:
fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()
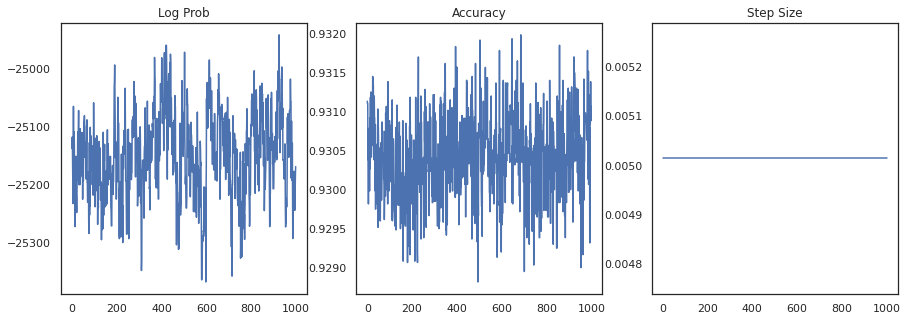
ถ้าเรารวมกลุ่มตัวอย่าง เราสามารถคำนวณค่าเฉลี่ยของแบบจำลองเบย์เพื่อปรับปรุงประสิทธิภาพของเรา
@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
images, labels = data
logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
probs = jax.nn.softmax(logits, axis=-1)
bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')
sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')
Average Accuracy: 0.9188529253005981 BMA Accuracy: 0.9264000058174133 Accuracy Improvement: 0.0075470805168151855
ค่าเฉลี่ยของแบบจำลองเบย์ทำให้ความแม่นยำของเราเพิ่มขึ้นเกือบ 1%!
ตัวอย่าง: ระบบแนะนำ MovieLens
ตอนนี้ เรามาลองอนุมานด้วยชุดข้อมูลคำแนะนำของ MovieLens ซึ่งเป็นกลุ่มผู้ใช้และการให้คะแนนของภาพยนตร์ต่างๆ โดยเฉพาะเราสามารถเป็นตัวแทนของ MovieLens เป็น \(N \times M\) นาฬิกาเมทริกซ์ \(W\) ที่ \(N\) เป็นจำนวนผู้ใช้และ \(M\) เป็นจำนวนของภาพยนตร์; เราคาดว่า \(N > M\)รายการของ \(W_{ij}\) เป็นบูลแสดงให้เห็นหรือไม่ว่าผู้ใช้ \(i\) ดูหนัง \(j\)โปรดทราบว่า MovieLens ให้การให้คะแนนแก่ผู้ใช้ แต่เราไม่สนใจพวกเขาเพื่อทำให้ปัญหาง่ายขึ้น
อันดับแรก เราจะโหลดชุดข้อมูล เราจะใช้เวอร์ชันที่มีคะแนน 1 ล้าน
movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']
Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0... HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl… HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value=''))) Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value=''))) Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.
เราจะทำบาง preprocessing ของชุดข้อมูลที่จะได้รับนาฬิกาเมทริกซ์ \(W\)
raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']
movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])
num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1
movie_titles = dict(zip(movielens['train']['movie_id'],
movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]
watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)
(6040, 3706)
เราสามารถกำหนดรูปแบบการกำเนิดสำหรับ \(W\)โดยใช้รูปแบบความน่าจะเป็นตัวประกอบเมทริกซ์ที่เรียบง่าย เราถือว่าแฝง \(N \times D\) ใช้เมทริกซ์ \(U\) และแฝง \(M \times D\) หนังเมทริกซ์ \(V\)ซึ่งเมื่อคูณผลิต logits ของ Bernoulli สำหรับนาฬิกาเมทริกซ์ \(W\)นอกจากนี้เรายังจะรวมถึงพาหะอคติสำหรับผู้ใช้และภาพยนตร์ \(u\) และ \(v\)
\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]
นี่เป็นเมทริกซ์ที่ค่อนข้างใหญ่ ผู้ใช้ 6040 คนและภาพยนตร์ 3706 เรื่องนำไปสู่เมทริกซ์ที่มีรายการมากกว่า 22 ล้านรายการ เราจะเข้าใกล้การแบ่งส่วนโมเดลนี้อย่างไร ดีถ้าเราคิดว่า \(N > M\) (คือมีผู้ใช้มากกว่าภาพยนตร์) แล้วมันจะทำให้รู้สึกถึง Shard เมทริกซ์นาฬิกาทั่วแกนผู้ใช้เพื่อให้อุปกรณ์แต่ละตัวจะมีก้อนของนาฬิกาเมทริกซ์ที่สอดคล้องกับการย่อยของผู้ใช้เป็น . ซึ่งแตกต่างจากตัวอย่างก่อนหน้านี้ แต่เราจะยังมีการ Shard ขึ้น \(U\) เมทริกซ์เนื่องจากมีการฝังสำหรับผู้ใช้แต่ละดังนั้นอุปกรณ์ที่แต่ละคนจะต้องรับผิดชอบต่อการชาร์ดของ \(U\) และเศษของ \(W\). บนมืออื่น ๆ , \(V\) จะ unsharded และทำข้อมูลให้ตรงกันในอุปกรณ์
sharded_watch_matrix = shard(watch_matrix)
ก่อนที่เราจะเขียนของเรา run ให้ได้อย่างรวดเร็วหารือเกี่ยวกับความท้าทายเพิ่มเติมกับ sharding ท้องถิ่นตัวแปรสุ่ม \(U\)เมื่อใช้ HMC, วานิลลา tfp.mcmc.HamiltonianMonteCarlo เคอร์เนลจะลิ้มลองสักครู่สำหรับองค์ประกอบของรัฐห่วงโซ่ของแต่ละ ก่อนหน้านี้ เฉพาะตัวแปรสุ่มที่ไม่ได้แบ่งส่วนข้อมูลเท่านั้นที่เป็นส่วนหนึ่งของสถานะนั้น และโมเมนต์ก็เหมือนกันในแต่ละอุปกรณ์ เมื่อตอนนี้เรามี sharded \(U\)เราต้องลิ้มลองสักครู่ที่แตกต่างกันบนอุปกรณ์สำหรับแต่ละ \(U\)ในขณะที่การสุ่มตัวอย่างสักครู่เหมือนกันสำหรับ \(V\)เพื่อให้บรรลุนี้เราสามารถใช้ tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo กับ Sharded กระจายโมเมนตัม ขณะที่เราดำเนินการคำนวณแบบขนานระดับเฟิร์สคลาสต่อไป เราอาจลดความซับซ้อนของสิ่งนี้ เช่น โดยการนำตัวบ่งชี้การแบ่งส่วนไปที่เคอร์เนล HMC
def make_run(*,
axis_name,
dim=20,
num_chains=2,
prior_variance=1.,
step_size=1e-2,
num_leapfrog_steps=100,
num_burnin_steps=1000,
num_results=500,
):
@functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
@jax.default_matmul_precision('tensorfloat32')
def run(key, watch_matrix):
num_users, num_movies = watch_matrix.shape
Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)
def prior_fn():
user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
return (user_embeddings, user_bias, movie_embeddings, movie_bias)
prior = tfed.JointDistributionCoroutine(prior_fn)
def model_fn():
user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
+ user_bias[..., :, None] + movie_bias[..., None, :])
yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
model = tfed.JointDistributionCoroutine(model_fn)
init_key, sample_key = random.split(key)
initial_state = prior.sample(seed=init_key, sample_shape=num_chains)
def target_log_prob(*state):
return model.log_prob((*state, watch_matrix))
momentum_distribution = tfed.JointDistributionSequential([
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
])
# We pass in momentum_distribution here to ensure that the momenta for
# user_embeddings and user_bias are also sharded
kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
num_leapfrog_steps,
momentum_distribution=momentum_distribution)
num_adaptation_steps = int(0.8 * num_burnin_steps)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)
def trace_fn(state, pkr):
return {
'log_prob': target_log_prob(*state),
'log_accept_ratio': pkr.inner_results.log_accept_ratio,
}
return tfm.sample_chain(
num_results, initial_state,
kernel=kernel,
num_burnin_steps=num_burnin_steps,
trace_fn=trace_fn,
seed=sample_key)
return run
เราจะใช้มันอีกครั้งในการแคชที่รวบรวม run
%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)
CPU times: user 56 s, sys: 1min 24s, total: 2min 20s Wall time: 3min 35s
ตอนนี้เราจะเรียกใช้อีกครั้งโดยไม่มีการคอมไพล์โอเวอร์เฮด
%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)
CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s Wall time: 3min 1s
ดูเหมือนว่าเราจะก้าวกระโดดประมาณ 150,000 ก้าวในเวลาประมาณ 3 นาที ดังนั้นประมาณ 83 ก้าวกระโดดต่อวินาที! มาพลอตอัตราส่วนการยอมรับและบันทึกความหนาแน่นของตัวอย่างของเรากัน
fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
ax.plot(val[0]) # Indexing into a sharded array, each element is the same
ax.set_title(key);
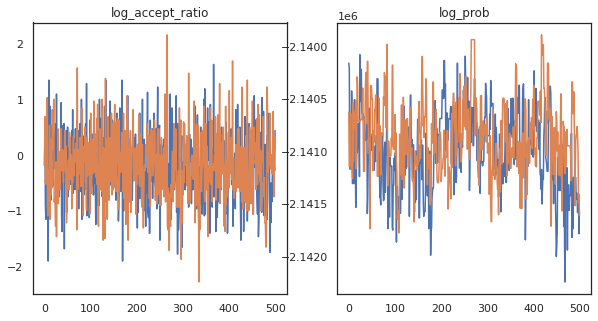
ตอนนี้เรามีตัวอย่างบางส่วนจากเครือ Markov ของเราแล้ว มาลองใช้พวกมันเพื่อทำนายกัน ขั้นแรก ให้แยกส่วนประกอบแต่ละส่วนออกก่อน โปรดจำไว้ว่า user_embeddings และ user_bias มีแยกข้ามอุปกรณ์ดังนั้นเราจึงจำเป็นที่จะต้องเชื่อมเรา ShardedArray ที่จะได้รับพวกเขาทั้งหมด บนมืออื่น ๆ , movie_embeddings และ movie_bias จะเหมือนกันในอุปกรณ์ทุกดังนั้นเราก็สามารถเลือกค่าจากสะเก็ดแรก เราจะใช้ปกติ numpy เพื่อคัดลอกค่าจาก TPUs กลับไป CPU
user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')
User embeddings: (500, 2, 6040, 20) User bias: (500, 2, 6040) Movie embeddings: (500, 2, 3706, 20) Movie bias: (500, 2, 3706)
มาลองสร้างระบบผู้แนะนำอย่างง่ายที่ใช้ความไม่แน่นอนที่รวบรวมไว้ในตัวอย่างเหล่านี้ อันดับแรก มาเขียนฟังก์ชันที่จัดอันดับภาพยนตร์ตามความน่าจะเป็นในการรับชมกันก่อน
@jax.jit
def recommend(sample, user_id):
user_embeddings, user_bias, movie_embeddings, movie_bias = sample
movie_logits = (
jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
+ user_bias[user_id] + movie_bias)
return movie_logits.argsort()[::-1]
ตอนนี้ เราสามารถเขียนฟังก์ชันที่วนซ้ำตัวอย่างทั้งหมด และสำหรับแต่ละตัวอย่าง เลือกภาพยนตร์อันดับต้น ๆ ที่ผู้ใช้ยังไม่ได้ดู จากนั้นเราจะดูจำนวนภาพยนตร์ที่แนะนำทั้งหมดในกลุ่มตัวอย่างได้
def get_recommendations(user_id):
movie_ids = []
already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
for i in range(500):
for j in range(2):
sample = jax.tree_map(lambda x: x[i, j], samples)
ranking = recommend(sample, user_id)
for movie_id in ranking:
if int(movie_id) not in already_watched:
movie_ids.append(movie_id)
break
return movie_ids
def plot_recommendations(movie_ids, ax=None):
titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
ax = ax or plt.gca()
names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
ax.bar(names, counts)
ax.set_xticklabels(names, rotation=90)
พิจารณาผู้ใช้ที่ดูภาพยนตร์มากที่สุด เทียบกับผู้ใช้ที่ดูน้อยที่สุด
user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])
2314 20
เราหวังว่าระบบของเรามีความเชื่อมั่นมากขึ้นเกี่ยวกับ user_most กว่า user_least ระบุว่าเรามีข้อมูลเพิ่มเติมเกี่ยวกับสิ่งที่ประเภทของภาพยนตร์ user_most มีแนวโน้มที่จะดู
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');
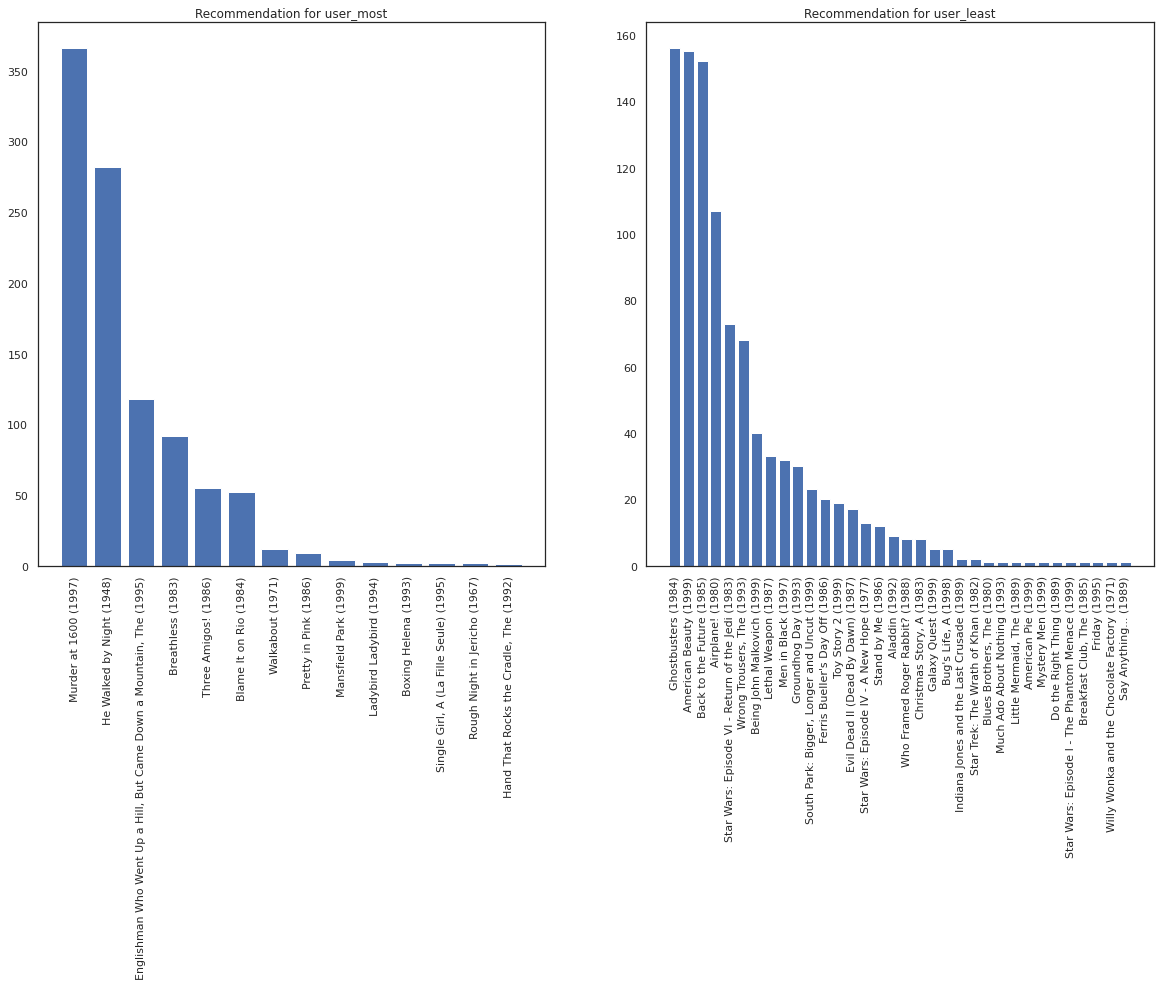
เราจะเห็นว่ามีความแปรปรวนมากขึ้นในคำแนะนำของเราสำหรับ user_least สะท้อนให้เห็นถึงความไม่แน่นอนที่เพิ่มขึ้นของเราในการตั้งค่านาฬิกาของพวกเขา
นอกจากนี้เรายังสามารถดูประเภทของภาพยนตร์ที่แนะนำ
most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');
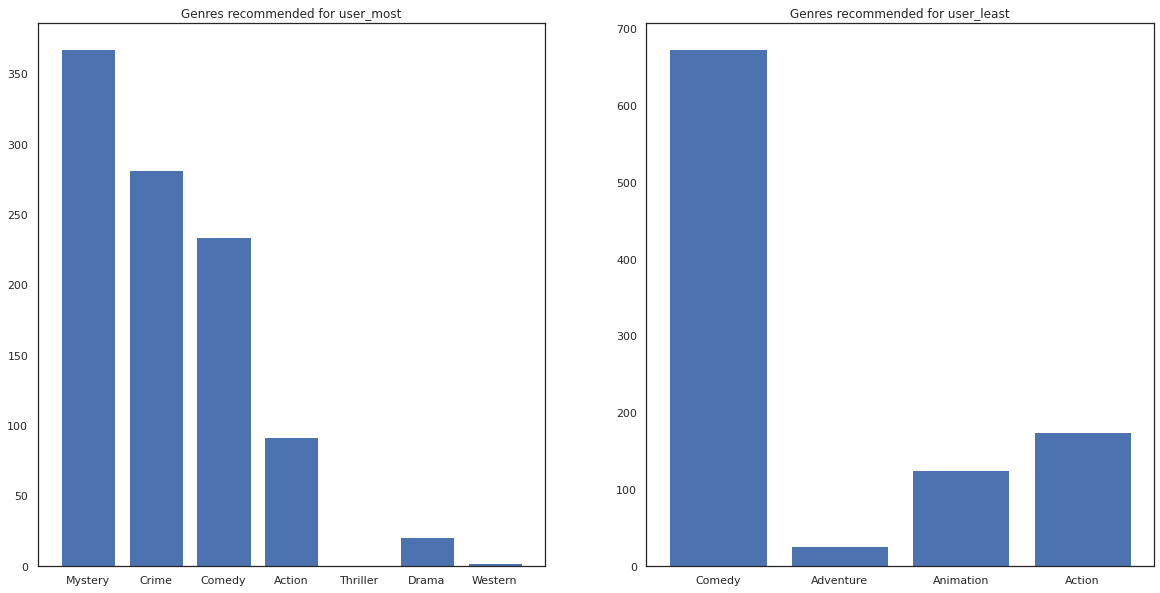
user_most ได้เห็นมากของภาพยนตร์และได้รับการแนะนำประเภทเฉพาะมากขึ้นเช่นความลึกลับและอาชญากรรมในขณะที่ user_least ยังไม่ได้ดูหนังจำนวนมากและได้รับการแนะนำภาพยนตร์กระแสหลักมากขึ้นซึ่งตลกเอียงและการกระทำ
