 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запускаем в Google Colab Запускаем в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
TensorFlow Probability (TFP) на JAX теперь имеет инструменты для распределенных численных вычислений. Для масштабирования до большого количества ускорителей инструменты построены на написании кода с использованием парадигмы «одна программа с несколькими данными», или сокращенно SPMD.
В этом блокноте мы рассмотрим, как «мыслить в SPMD», и представим новые абстракции TFP для масштабирования до таких конфигураций, как модули TPU или кластеры графических процессоров. Если вы запускаете этот код самостоятельно, обязательно выберите среду выполнения TPU.
Сначала мы установим последние версии TFP, JAX и TF.
Устанавливает
pip install jaxlib --upgrade -q 2>&1 1> /dev/nullpip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/nullpip install tf-nightly-cpu -q -I 2>&1 1> /dev/nullpip install jax -I -q --upgrade 2>&1 1>/dev/null
Мы импортируем некоторые общие библиотеки вместе с некоторыми утилитами JAX.
Настройка и импорт
import functools
import collections
import contextlib
import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds
from tensorflow_probability.substrates import jax as tfp
sns.set(style='white')
INFO:tensorflow:Enabling eager execution INFO:tensorflow:Enabling v2 tensorshape INFO:tensorflow:Enabling resource variables INFO:tensorflow:Enabling tensor equality INFO:tensorflow:Enabling control flow v2
Мы также настроим несколько удобных псевдонимов TFP. Новые абстракции в настоящее время предоставляется в tfp.experimental.distribute и tfp.experimental.mcmc .
tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc
Root = tfed.JointDistributionCoroutine.Root
Для подключения ноутбука к TPU воспользуемся следующим помощником от JAX. Чтобы подтвердить, что мы подключены, мы распечатываем количество устройств, которых должно быть восемь.
from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')
Found 8 devices
Быстрое введение в jax.pmap
После подключения к ТПУ, мы имеем доступ к восьми устройствам. Однако, когда мы нетерпеливо запускаем код JAX, JAX по умолчанию запускает вычисления только на одном.
Самый простой способ выполнения вычислений на многих устройствах - это сопоставление функции, при которой каждое устройство выполняет один индекс карты. JAX обеспечивает jax.pmap ( «параллельная карта») преобразование , которое превращает функцию в одну , которая отображает функцию по нескольким устройствам.
В следующем примере мы создаем массив размером 8 (чтобы соответствовать количеству доступных устройств) и сопоставляем функцию, которая добавляет к нему 5.
xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)
<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5. 6. 7. 8. 9. 10. 11. 12.]
Обратите внимание , что мы получаем ShardedDeviceArray типа обратно, указывая , что выходной массив физически разделен между устройствами.
jax.pmap действует семантический как карта, но имеет несколько важных параметров , которые изменяют свое поведение. По умолчанию pmap принимает все входные данные для функции, которые отображаются в течение, но мы можем изменить это поведение с помощью in_axes аргумента.
xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)
[ 5. 6. 7. 8. 9. 10. 11. 12.]
Аналогично, out_axes аргумент pmap определяет , является ли или не возвращать значения на каждом устройстве. Установка out_axes в None автоматически возвращает значение на 1 - ом устройстве и должны использоваться только тогда , когда мы уверены в том, что значения одинаковы на каждом устройстве.
xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)
2.0
Что происходит, когда то, что мы хотели бы сделать, нелегко выразить в виде отображаемой чистой функции? Например, что, если мы хотим вычислить сумму по оси, которую мы отображаем? JAX предлагает «коллективы», функции, которые взаимодействуют между устройствами, что позволяет писать более интересные и сложные распределенные программы. Чтобы понять, как именно они работают, мы познакомим вас с SPMD.
Что такое СПМД?
Одна программа с множественными данными (SPMD) - это модель параллельного программирования, в которой одна программа (то есть один и тот же код) выполняется одновременно на всех устройствах, но входные данные для каждой из запущенных программ могут отличаться.
Если наша программа является простой функцией его входов (то есть что - то вроде x + 5 ), запуск программы в SPMD только отображение его на различные данные, как мы это делали с jax.pmap ранее. Однако мы можем делать больше, чем просто «отображать» функцию. JAX предлагает «коллективы», то есть функции, которые обмениваются данными между устройствами.
Например, возможно, мы хотели бы получить сумму количества по всем нашим устройствам. Перед тем , как сделать это, нам нужно присвоить имя оси мы картирование над в pmap . Затем мы используем lax.psum ( «параллельная сумму») функцию для выполнения суммы на всех устройства, обеспечивая отождествить именованную ось мы суммируя.
def f(x):
out = lax.psum(x, axis_name='i')
return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)
ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)
psum коллективные агрегаты Значение x на каждом устройстве и синхронизирует его значение по всей карте , т.е. out является 28. на каждом устройстве. Мы больше не выполняем простую «карту», но выполняем программу SPMD, в которой вычисления каждого устройства теперь могут взаимодействовать с такими же вычислениями на других устройствах, хотя и ограниченным образом с использованием коллективов. В этом случае мы можем использовать out_axes = None , потому что psum синхронизирует значение.
def f(x):
out = lax.psum(x, axis_name='i')
return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))
ShardedDeviceArray(28., dtype=float32)
SPMD позволяет нам написать одну программу, которая запускается на каждом устройстве в любой конфигурации TPU одновременно. Тот же код, который используется для машинного обучения на 8 ядрах TPU, можно использовать в модуле TPU, который может иметь от сотен до тысяч ядер! Для более подробного учебника о jax.pmap и SPMD, вы можете обратиться к JAX 101 учебника .
MCMC в масштабе
В этой записной книжке мы сосредоточимся на использовании методов Монте-Карло цепи Маркова (MCMC) для байесовского вывода. Есть несколько способов использования многих устройств для MCMC, но в этом ноутбуке мы сосредоточимся на двух:
- Запуск независимых цепей Маркова на разных устройствах. Этот случай довольно простой и его можно обойтись ванильным TFP.
- Разделение набора данных между устройствами. Этот случай немного сложнее и требует недавно добавленного оборудования TFP.
Независимые цепи
Допустим, мы хотим сделать байесовский вывод по проблеме с использованием MCMC и хотим запустить несколько цепочек параллельно на нескольких устройствах (скажем, по 2 на каждом устройстве). Оказывается, это программа, которую мы можем просто «сопоставить» по устройствам, то есть программа, которая не нуждается в коллективах. Чтобы убедиться, что каждая программа выполняет разные цепи Маркова (а не одну и ту же), мы передаем разные значения для случайного начального числа каждому устройству.
Давайте попробуем это на игрушечной задаче выборки из двумерного распределения Гаусса. Мы можем использовать существующие функциональные возможности MCMC TFP из коробки. В общем, мы стараемся поместить большую часть логики в нашу отображаемую функцию, чтобы более четко различать то, что работает на всех устройствах, и только первое.
def run(seed):
target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob
initial_state = jnp.zeros([2, 2]) # 2 chains
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
def trace_fn(state, pkr):
return target_log_prob(state)
states, log_prob = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
kernel=kernel,
current_state=initial_state,
trace_fn=trace_fn,
seed=seed
)
return states, log_prob
Сам по себе run функция принимает в безгосударственном случайном семени (чтобы увидеть , как без гражданства хаотичности работы, вы можете прочитать TFP на JAX ноутбуке или увидеть JAX 101 учебник ). Mapping run по различным семенам приведет работают несколько независимых цепей Маркова.
states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)
(8, 1000, 2, 2) (8, 1000, 2)
Обратите внимание, что теперь у нас есть дополнительная ось, соответствующая каждому устройству. Мы можем изменить размеры и сгладить их, чтобы получить ось для 16 цепей.
states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()
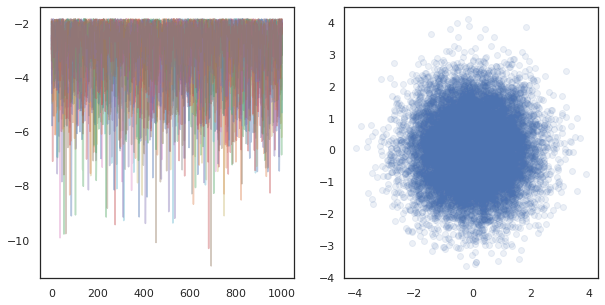
При работе независимых цепей на многих устройствах, это так просто , как pmap -ный над функцией , которая использует tfp.mcmc , обеспечивая нам пройти различные значения для случайного семени к каждому устройству.
Данные шардинга
Когда мы проводим MCMC, целевое распределение часто представляет собой апостериорное распределение, полученное путем кондиционирования набора данных, а вычисление ненормализованной логарифмической плотности включает суммирование правдоподобий для каждой наблюдаемой информации.
С очень большими наборами данных может быть непомерно дорого даже запускать одну цепочку на одном устройстве. Однако, когда у нас есть доступ к нескольким устройствам, мы можем разделить набор данных между устройствами, чтобы лучше использовать имеющиеся у нас вычислительные ресурсы.
Если бы мы хотели сделать MCMC с sharded набора данных, мы должны обеспечить ненормализованное логарифмической плотности вычисляем на каждом устройстве представляет собой итог, то есть плотность по всем данным, в противном случае каждое устройство будет делать MCMC со своей неверной цели распределение. С этой целью, TFP теперь имеет новые инструменты (т.е. tfp.experimental.distribute и tfp.experimental.mcmc ) , которые позволяют вычисления «sharded» вероятности журнала и делать MCMC с ними.
Разделенные распределения
Ядро абстракции СФП теперь обеспечивает для вычисления sharded probabiliities журнала представляет собой Sharded мета-распределение, которое принимает распределение в качестве входных данных и возвращает новое распределение , которое имеет специфические свойства , которые при выполнении в контексте SPMD. Sharded живет в tfp.experimental.distribute .
Интуитивно, Sharded распределение соответствует набору случайных величин , которые были «разделить» на разных устройствах. На каждом устройстве они будут производить разные образцы и индивидуально могут иметь разную логарифмическую плотность. В качестве альтернативы, Sharded распределение соответствует «пластины» в графической модели просторечии, где размер пластины является количество устройств.
Отбор проб Sharded распределение
Если образец из Normal распределения в передающейся pmap -ed с использованием того же семени на каждом устройстве, мы получим тот же образец на каждом устройстве. Мы можем рассматривать следующую функцию как выборку одной случайной переменной, которая синхронизируется между устройствами.
# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32)
Если завернуть tfd.Normal(0., 1.) с tfed.Sharded , мы логически теперь имеют восемь различных случайных величин ( по одному на каждое устройство) и , следовательно , будет производить различный образец для каждого из них, несмотря на прохождение в том же семени .
def f(seed, _):
return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([ 1.2152631 , 0.7818249 , 0.32549605, 0.6828047 ,
1.3973192 , -0.57830244, 0.37862757, 2.7706041 ], dtype=float32)
Эквивалентное представление этого распределения на одном устройстве - это всего лишь 8 независимых нормальных выборок. Даже если значение образца будет отличаться ( tfed.Sharded делает псевдо-генерации случайных чисел несколько иначе), они оба представляют собой то же самое распределение.
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))
DeviceArray([ 0.08086783, -0.38624594, -0.3756545 , 1.668957 ,
-1.2758069 , 2.1192007 , -0.85821325, 1.1305912 ], dtype=float32)
Принимая логарифмическую плотность Sharded распределения
Давайте посмотрим, что произойдет, когда мы вычислим логарифмическую плотность выборки из регулярного распределения в контексте SPMD.
def f(seed, _):
dist = tfd.Normal(0., 1.)
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32),
ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
-0.94012403, -0.94012403, -0.94012403, -0.94012403], dtype=float32))
Каждый образец одинаков на каждом устройстве, поэтому мы вычисляем одинаковую плотность и на каждом устройстве. Интуитивно понятно, что здесь мы имеем распределение только по одной нормально распределенной переменной.
С Sharded распределением, мы имеем распределение по 8 случайных величин, поэтому , когда мы вычисляем log_prob образца, мы суммируем, на разных устройствах, по каждому из отдельных плотностей бревен. (Вы можете заметить, что это общее значение log_prob больше, чем одноэлементное значение log_prob, вычисленное выше.)
def f(seed, _):
dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)
Sample: [ 1.2152631 0.7818249 0.32549605 0.6828047 1.3973192 -0.57830244 0.37862757 2.7706041 ] Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205]
Эквивалентное "незакрашенное" распределение дает такую же плотность бревна.
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)
DeviceArray(-13.7349205, dtype=float32)
Sharded распределение производит различные значения из sample на каждом устройстве, но получить то же значение для log_prob на каждом устройстве. Что тут происходит? Sharded распределение делает psum внутри для того чтобы обеспечить log_prob значения находятся в синхронизации различных устройств. Зачем нам такое поведение? Если мы запустим тот же MCMC цепи на каждом устройстве, мы хотели бы , чтобы target_log_prob быть одинаковыми на каждом устройстве, даже если некоторые случайные переменные в вычислении являются sharded на разных устройствах.
Кроме того, через Sharded гарантирует , что градиенты распределение через устройство являются правильными, чтобы гарантировать , что алгоритмы , такие как HMC, которые принимают градиенты функции логарифма плотности как часть переходной функции, производят соответствующие образцы.
Sharded JointDistribution s
Мы можем создавать модели с несколькими Sharded случайных величин с помощью JointDistribution s (JDs). К сожалению, Sharded распределение не может быть безопасно использовано с ванильным tfd.JointDistribution s, но tfp.experimental.distribute экспорта «заплатой» JDS , которые ведут себя как Sharded распределения.
def f(seed, _):
dist = tfed.JointDistributionSequential([
tfd.Normal(0., 1.),
tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
])
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
1.6121525, 1.6121525, 1.6121525], dtype=float32),
ShardedDeviceArray([ 0.8690128 , -0.83167845, 1.2209264 , 0.88412696,
0.76478404, -0.66208494, -0.0129658 , 0.7391483 ], dtype=float32)],
ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
-12.214451, -12.214451, -12.214451, -12.214451], dtype=float32))
Этот sharded JDs может иметь как Sharded распределение и ваниль TFP в качестве компонентов. Для незакрепленных дистрибутивов мы получаем один и тот же образец на каждом устройстве, а для сегментированных дистрибутивов мы получаем разные образцы. log_prob на каждом устройстве синхронизации , а также.
MCMC с Sharded распределений
Как мы думаем о Sharded распределений в контексте MCMC? Если мы имеем порождающую модель , которая может быть выражена как JointDistribution , мы можем выбрать некоторую ось этой модели «осколок» в поперечнике. Как правило, одна случайная переменная в модели будет соответствовать наблюдаемым данным, и если у нас есть большой набор данных, который мы хотели бы сегментировать между устройствами, мы хотим, чтобы переменные, связанные с точками данных, также были сегментированы. У нас также могут быть «локальные» случайные переменные, которые взаимно однозначны с данными, которые мы сегментируем, поэтому нам придется дополнительно сегментировать эти случайные переменные.
Мы рассмотрим примеры использования Sharded распределений с TFP MCMC в этом разделе. Мы начнем с более простой байесовской логистической регрессии , например, и в заключение примере матрицы факторизации, с целью продемонстрировать некоторые примеры использования для distribute библиотеки.
Пример: байесовская логистическая регрессия для MNIST
Мы хотели бы провести байесовскую логистическую регрессию на большом наборе данных; модель имеет предварительное \(p(\theta)\) над весами регрессии, а также вероятность \(p(y_i | \theta, x_i)\) , что суммируется по всем данным \(\{x_i, y_i\}_{i = 1}^N\) , чтобы получить суммарную плотность совместного журнала. Если мы шард наших данных, мы шард наблюдаемых случайных величин \(x_i\) и \(y_i\) в нашей модели.
Мы используем следующую байесовскую модель логистической регрессии для классификации MNIST:
\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]
Загрузим MNIST с помощью наборов данных TensorFlow.
mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.
raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.
Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1... WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your local data directory. If you'd instead prefer to read directly from our public GCS bucket (recommended if you're running on GCP), you can instead pass `try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`. HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio… Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.
У нас есть 60000 обучающих образов, но давайте воспользуемся нашими 8 доступными ядрами и разделим их на 8 направлений. Мы будем использовать эту удобную shard функцию полезности.
def shard_value(x):
x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices
shard = functools.partial(jax.tree_map, shard_value)
sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)
(8, 7500, 784) (8, 7500)
Прежде чем продолжить, давайте быстро обсудим точность TPU и ее влияние на HMC. TPUs выполнить умножение матриц , используя низкую bfloat16 точность скорости. bfloat16 матрица умножений часто достаточно для многих глубоких приложений обучения, но при использовании HMC, мы эмпирически обнаружили , что нижняя точность может привести к расходящимся траекториям, вызывая отторжение. Мы можем использовать матричное умножение с более высокой точностью за счет некоторых дополнительных вычислений.
Для того, чтобы увеличить нашу matmul точности, мы можем использовать jax.default_matmul_precision декоратор с "tensorfloat32" точностью (для еще более высокой точности мы могли бы использовать "float32" точность).
Давайте определим нашу run функцию, которая будет принимать в случайном семени (который будет одинаковым на каждом устройстве) и осколок MNIST. Функция будет реализовывать вышеупомянутую модель, и затем мы будем использовать ванильную функциональность MCMC TFP для запуска одной цепочки. Мы позаботимся , чтобы украсить run с jax.default_matmul_precision декоратором , чтобы убедиться , умножение матриц выполняются с более высокой точностью, хотя в данном конкретном примере , приведенном ниже, мы могли бы точно также использовать jnp.dot(images, w, precision=lax.Precision.HIGH) .
# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device.
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
images, labels = data # a sharded dataset
num_examples, dim = images.shape
num_classes = 10
def model_fn():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
logits = jnp.dot(images, w) + b
yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
shard_axis_name='data')
model = tfed.JointDistributionCoroutine(model_fn)
init_seed, sample_seed = random.split(seed)
initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`
def target_log_prob(*state):
return model.log_prob((*state, labels))
def accuracy(w, b):
logits = images.dot(w) + b
preds = logits.argmax(axis=-1)
# We take the average accuracy across devices by using `lax.pmean`
return lax.pmean((preds == labels).mean(), 'data')
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
def trace_fn(state, pkr):
return (
target_log_prob(*state),
accuracy(*state),
pkr.new_step_size)
states, trace = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
current_state=initial_state,
kernel=kernel,
trace_fn=trace_fn,
seed=sample_seed
)
return states, trace
jax.pmap включает в себя JIT компиляции , но скомпилированные функции кэшируются после первого вызова. Мы будем называть run и игнорировать вывод в кэш компиляции.
%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)
CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s Wall time: 1min 54s
Теперь мы будем называть run снова , чтобы увидеть , как долго фактическое исполнение принимает.
%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)
CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s Wall time: 1min 43s
Мы выполняем 200 000 шагов, каждый из которых вычисляет градиент по всему набору данных. Разделение вычислений на 8 ядер позволяет нам вычислить эквивалент 200000 эпох обучения примерно за 95 секунд, примерно 2100 эпох в секунду!
Давайте построим логарифмическую плотность каждой выборки и точность каждой выборки:
fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()
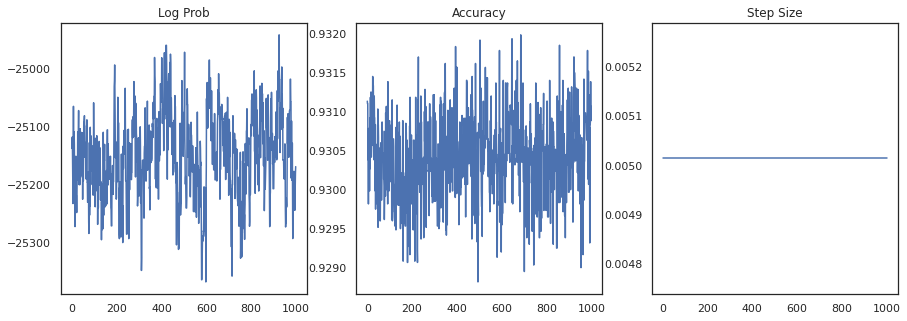
Если мы объединим образцы в ансамбль, мы сможем вычислить среднее значение байесовской модели, чтобы улучшить нашу производительность.
@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
images, labels = data
logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
probs = jax.nn.softmax(logits, axis=-1)
bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')
sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')
Average Accuracy: 0.9188529253005981 BMA Accuracy: 0.9264000058174133 Accuracy Improvement: 0.0075470805168151855
Среднее значение байесовской модели увеличивает нашу точность почти на 1%!
Пример: система рекомендаций MovieLens
Давайте теперь попробуем сделать вывод с помощью набора данных рекомендаций MovieLens, который представляет собой набор пользователей и их оценок различных фильмов. В частности, мы можем представить MovieLens в качестве \(N \times M\) часы матрицы \(W\) где \(N\) является количество пользователей и \(M\) это количество фильмов; мы ожидаем , что \(N > M\). Записи о \(W_{ij}\) являются логическое значение , указывающее ли или нет пользователь \(i\) смотрел фильм \(j\). Обратите внимание, что MovieLens предоставляет оценки пользователей, но мы игнорируем их, чтобы упростить задачу.
Сначала мы загрузим набор данных. Мы будем использовать версию с 1 миллионом оценок.
movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']
Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0... HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl… HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value=''))) Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value=''))) Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.
Мы сделаем некоторую предварительную обработку набора данных , чтобы получить часы матрицу \(W\).
raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']
movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])
num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1
movie_titles = dict(zip(movielens['train']['movie_id'],
movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]
watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)
(6040, 3706)
Мы можем определить порождающую модель для \(W\), используя простую вероятностную матрицу модель факторизации. Мы предполагаем , латентный \(N \times D\) матрицы пользователя \(U\) и латентную \(M \times D\) матрица фильма \(V\), который при умножении производить логит Бернулли для часов матрица \(W\). Мы будем также включать в себя смещение векторы для пользователей и фильмов, \(u\) и \(v\).
\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]
Это довольно большая матрица; 6040 пользователей и 3706 фильмов приводит к матрице с более чем 22 миллионами записей. Как мы подходим к сегментированию этой модели? Ну, если мы предположим , что \(N > M\) (т.е. есть больше пользователей , чем кино), то это имело бы смысл шард матрицы часов по всей оси пользователя, так что каждое устройство будет иметь кусок часов матрицы , соответствующий подгруппу пользователей . В отличии от предыдущего примера, однако, мы также должны шард вверх \(U\) матрицы, так как он имеет вложение для каждого пользователя, так что каждое устройство будет нести ответственность за осколок \(U\) и осколок \(W\). С другой стороны, \(V\) будет unsharded и быть синхронизированы между устройствами.
sharded_watch_matrix = shard(watch_matrix)
Перед тем , как написать наш run , давайте быстро обсудят дополнительные проблемы с шардингом местного случайными переменной \(U\). При работе HMC, ваниль tfp.mcmc.HamiltonianMonteCarlo ядра будет продегустировать импульсы для каждого элемента состояния цепного в. Раньше в это состояние входили только незашифрованные случайные величины, и импульсы были одинаковыми на всех устройствах. Когда мы теперь имеем sharded \(U\), мы должны попробовать разные импульсы на каждое устройстве для \(U\), пробуя те же импульсы для \(V\). Для достижения этой цели , мы можем использовать tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo с Sharded распределения импульса. Поскольку мы продолжаем делать параллельные вычисления первоклассными, мы можем упростить это, например, перенеся индикатор сегментированности в ядро HMC.
def make_run(*,
axis_name,
dim=20,
num_chains=2,
prior_variance=1.,
step_size=1e-2,
num_leapfrog_steps=100,
num_burnin_steps=1000,
num_results=500,
):
@functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
@jax.default_matmul_precision('tensorfloat32')
def run(key, watch_matrix):
num_users, num_movies = watch_matrix.shape
Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)
def prior_fn():
user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
return (user_embeddings, user_bias, movie_embeddings, movie_bias)
prior = tfed.JointDistributionCoroutine(prior_fn)
def model_fn():
user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
+ user_bias[..., :, None] + movie_bias[..., None, :])
yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
model = tfed.JointDistributionCoroutine(model_fn)
init_key, sample_key = random.split(key)
initial_state = prior.sample(seed=init_key, sample_shape=num_chains)
def target_log_prob(*state):
return model.log_prob((*state, watch_matrix))
momentum_distribution = tfed.JointDistributionSequential([
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
])
# We pass in momentum_distribution here to ensure that the momenta for
# user_embeddings and user_bias are also sharded
kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
num_leapfrog_steps,
momentum_distribution=momentum_distribution)
num_adaptation_steps = int(0.8 * num_burnin_steps)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)
def trace_fn(state, pkr):
return {
'log_prob': target_log_prob(*state),
'log_accept_ratio': pkr.inner_results.log_accept_ratio,
}
return tfm.sample_chain(
num_results, initial_state,
kernel=kernel,
num_burnin_steps=num_burnin_steps,
trace_fn=trace_fn,
seed=sample_key)
return run
Мы снова будем запускать один раз в кэше скомпилированной run .
%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)
CPU times: user 56 s, sys: 1min 24s, total: 2min 20s Wall time: 3min 35s
Теперь мы снова запустим его без дополнительных затрат на компиляцию.
%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)
CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s Wall time: 3min 1s
Похоже, мы сделали около 150 000 шагов прыжка за 3 минуты, то есть примерно 83 шага в секунду! Давайте изобразим коэффициент принятия и логарифмическую плотность наших образцов.
fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
ax.plot(val[0]) # Indexing into a sharded array, each element is the same
ax.set_title(key);
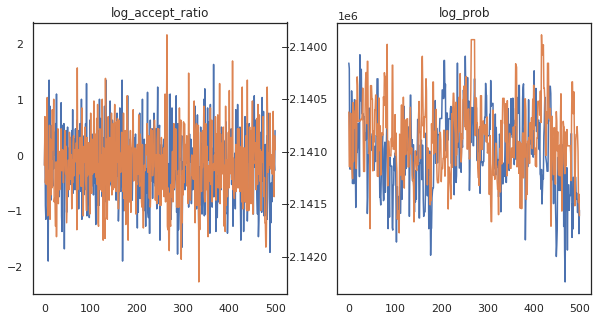
Теперь, когда у нас есть несколько примеров из нашей цепи Маркова, давайте воспользуемся ими, чтобы сделать некоторые прогнозы. Сначала извлечем каждый из компонентов. Помните , что user_embeddings и user_bias разделены на два разных устройства, поэтому мы должны объединить наши ShardedArray , чтобы получить их все. С другой стороны, movie_embeddings и movie_bias одинаковы на каждом устройстве, так что мы можем просто выбрать значение из первого осколка. Мы будем использовать регулярный numpy скопировать значения из TPUs обратно в центральный процессор.
user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')
User embeddings: (500, 2, 6040, 20) User bias: (500, 2, 6040) Movie embeddings: (500, 2, 3706, 20) Movie bias: (500, 2, 3706)
Давайте попробуем построить простую рекомендательную систему, которая использует погрешность, зафиксированную в этих выборках. Давайте сначала напишем функцию, которая ранжирует фильмы по вероятности просмотра.
@jax.jit
def recommend(sample, user_id):
user_embeddings, user_bias, movie_embeddings, movie_bias = sample
movie_logits = (
jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
+ user_bias[user_id] + movie_bias)
return movie_logits.argsort()[::-1]
Теперь мы можем написать функцию, которая перебирает все образцы и для каждого выбирает фильм с самым высоким рейтингом, который пользователь еще не смотрел. Затем мы можем увидеть количество всех рекомендованных фильмов в выборках.
def get_recommendations(user_id):
movie_ids = []
already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
for i in range(500):
for j in range(2):
sample = jax.tree_map(lambda x: x[i, j], samples)
ranking = recommend(sample, user_id)
for movie_id in ranking:
if int(movie_id) not in already_watched:
movie_ids.append(movie_id)
break
return movie_ids
def plot_recommendations(movie_ids, ax=None):
titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
ax = ax or plt.gca()
names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
ax.bar(names, counts)
ax.set_xticklabels(names, rotation=90)
Давайте возьмем пользователя, который посмотрел больше всего фильмов, и того, кто смотрел меньше всего.
user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])
2314 20
Мы надеемся , что наша система имеет большую определенность относительно user_most чем user_least , учитывая , что у нас есть больше информации о том, что сортирует фильмы user_most , скорее всего , смотреть.
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');
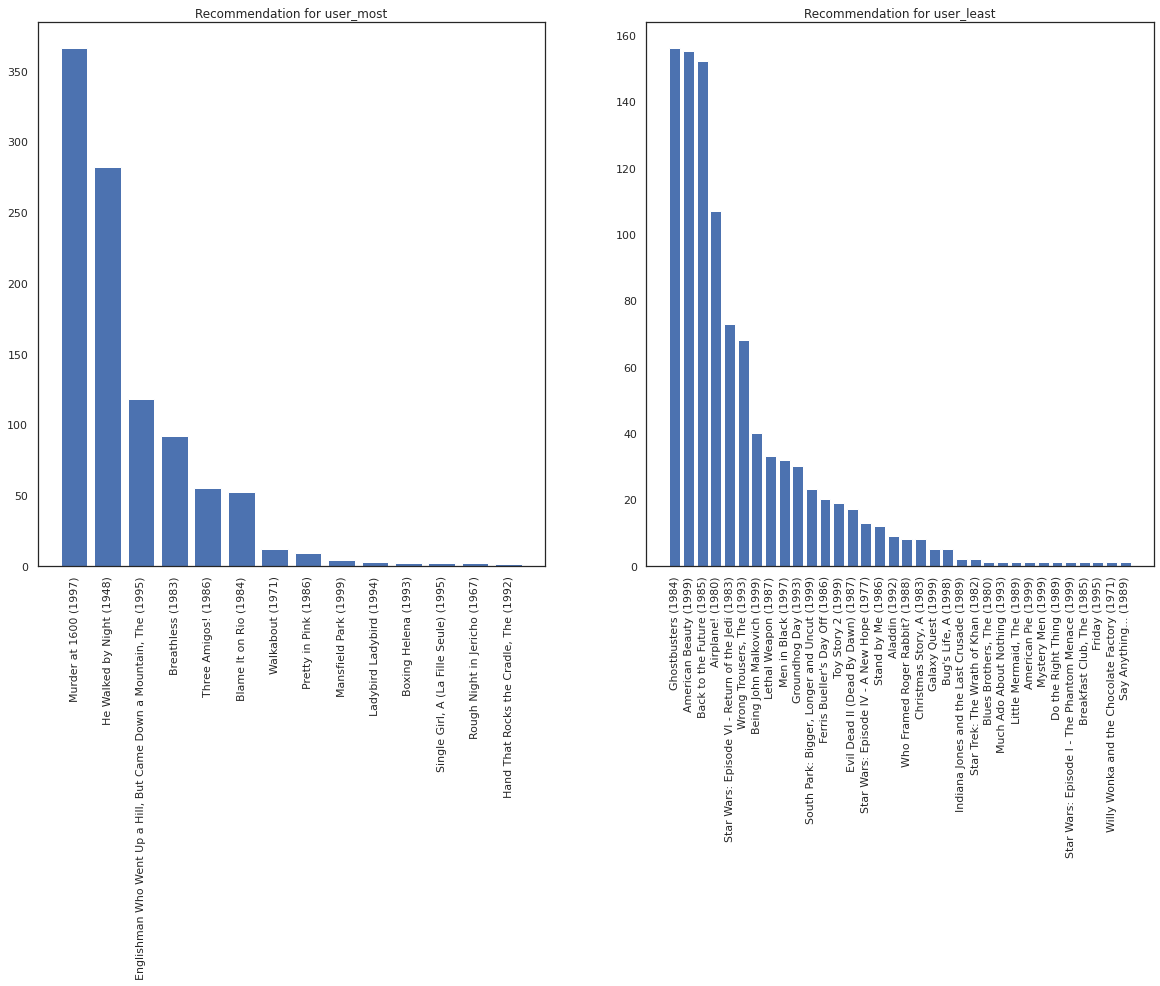
Мы видим , что есть еще разница в наших рекомендациях для user_least отражает нашу дополнительную неопределенность в своих часовых предпочтениях.
Также мы можем посмотреть жанры рекомендованных фильмов.
most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');
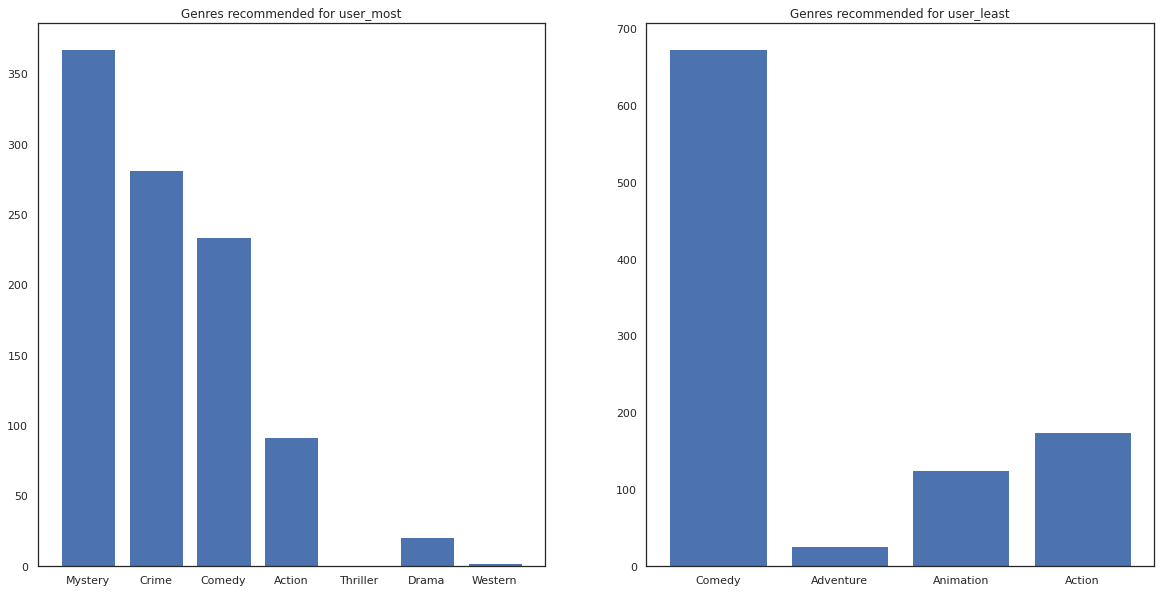
user_most видел много фильмов и было рекомендовано более нишевые жанры , как тайны и преступления , в то время как user_least не смотрел много фильмов , и было рекомендовано больше господствующих фильмов, который косо комедии и действия.
