 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
TensorFlow Probability (TFP) no JAX agora tem ferramentas para computação numérica distribuída. Para escalar para um grande número de aceleradores, as ferramentas são construídas em torno da escrita de código usando o paradigma de "dados múltiplos de programa único", ou SPMD, para abreviar.
Neste bloco de notas, veremos como "pensar em SPMD" e apresentar as novas abstrações TFP para dimensionamento para configurações como pods de TPU ou clusters de GPUs. Se você mesmo estiver executando este código, certifique-se de selecionar um tempo de execução de TPU.
Primeiro instalaremos as versões mais recentes TFP, JAX e TF.
Instalações
pip install jaxlib --upgrade -q 2>&1 1> /dev/nullpip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/nullpip install tf-nightly-cpu -q -I 2>&1 1> /dev/nullpip install jax -I -q --upgrade 2>&1 1>/dev/null
Vamos importar algumas bibliotecas gerais, junto com alguns utilitários JAX.
Configuração e importações
import functools
import collections
import contextlib
import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds
from tensorflow_probability.substrates import jax as tfp
sns.set(style='white')
INFO:tensorflow:Enabling eager execution INFO:tensorflow:Enabling v2 tensorshape INFO:tensorflow:Enabling resource variables INFO:tensorflow:Enabling tensor equality INFO:tensorflow:Enabling control flow v2
Também configuraremos alguns apelidos TFP úteis. As novas abstrações são atualmente prestados na tfp.experimental.distribute e tfp.experimental.mcmc .
tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc
Root = tfed.JointDistributionCoroutine.Root
Para conectar o notebook a uma TPU, usamos o seguinte auxiliar de JAX. Para confirmar que estamos conectados, imprimimos o número de dispositivos, que deve ser oito.
from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')
Found 8 devices
Uma rápida introdução à jax.pmap
Depois de se conectar a um TPU, temos acesso a oito dispositivos. No entanto, quando executamos o código JAX avidamente, o padrão JAX é executar cálculos em apenas um.
A maneira mais simples de executar um cálculo em muitos dispositivos é mapear uma função, fazendo com que cada dispositivo execute um índice do mapa. JAX fornece a jax.pmap ( "mapa paralelo") transformação que transforma uma função em um que mapeia a função em vários dispositivos.
No exemplo a seguir, criamos uma matriz de tamanho 8 (para corresponder ao número de dispositivos disponíveis) e mapeamos uma função que adiciona 5 a ela.
xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)
<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5. 6. 7. 8. 9. 10. 11. 12.]
Note que recebemos um ShardedDeviceArray tipo de volta, indicando que a matriz de saída está fisicamente dividida entre dispositivos.
jax.pmap atua semanticamente como um mapa, mas tem algumas opções importantes que modificam seu comportamento. Por padrão, pmap assume todas as entradas para a função estão sendo mapeados ao longo, mas podemos modificar esse comportamento com o in_axes argumento.
xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)
[ 5. 6. 7. 8. 9. 10. 11. 12.]
Analogamente, o out_axes argumento para pmap determina se deve ou não retornar os valores em cada dispositivo. Definir out_axes para None retorna automaticamente o valor no 1º dispositivo e só deve ser usado se estamos confiantes os valores são os mesmos em todos os dispositivos.
xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)
2.0
O que acontece quando o que gostaríamos de fazer não é facilmente expressável como uma função pura mapeada? Por exemplo, e se quisermos fazer uma soma ao longo do eixo que estamos mapeando? JAX oferece "coletivos", funções que se comunicam entre dispositivos, para permitir a escrita de programas distribuídos mais interessantes e complexos. Para entender exatamente como eles funcionam, apresentaremos o SPMD.
O que é SPMD?
Dados múltiplos de programa único (SPMD) é um modelo de programação simultânea no qual um único programa (ou seja, o mesmo código) é executado simultaneamente nos dispositivos, mas as entradas para cada um dos programas em execução podem ser diferentes.
Se o nosso programa é uma simples função de suas entradas (ou seja, algo como x + 5 ), executando um programa em SPMD é apenas mapeando-os dados sobre diferentes, como fizemos com jax.pmap anteriormente. No entanto, podemos fazer mais do que apenas "mapear" uma função. JAX oferece "coletivos", que são funções que se comunicam entre dispositivos.
Por exemplo, talvez gostaríamos de calcular a soma de uma quantidade em todos os nossos dispositivos. Antes de fazermos isso, precisamos atribuir um nome ao que nós eixo está mapeando mais na pmap . Em seguida, usamos o lax.psum função ( "soma paralela") para realizar uma soma entre dispositivos, assegurando que identificamos o chamado eixo estamos somando.
def f(x):
out = lax.psum(x, axis_name='i')
return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)
ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)
O psum agregados coletivos o valor de x em cada dispositivo e sincroniza o seu valor através do mapa, ou seja, out é 28. em cada dispositivo. Não estamos mais realizando um simples "mapa", mas sim um programa SPMD onde a computação de cada dispositivo pode agora interagir com a mesma computação em outros dispositivos, embora de forma limitada usando coletivos. Neste cenário, podemos usar out_axes = None , porque psum irá sincronizar o valor.
def f(x):
out = lax.psum(x, axis_name='i')
return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))
ShardedDeviceArray(28., dtype=float32)
O SPMD nos permite escrever um programa que é executado em todos os dispositivos em qualquer configuração de TPU simultaneamente. O mesmo código usado para fazer aprendizado de máquina em 8 núcleos de TPU pode ser usado em um pod de TPU que pode ter centenas a milhares de núcleos! Para um tutorial mais detalhadas sobre jax.pmap e SPMD, você pode consultar a do JAX 101 tutorial .
MCMC em escala
Neste caderno, nos concentramos no uso de métodos Markov Chain Monte Carlo (MCMC) para inferência Bayesiana. Pode haver maneiras de utilizar muitos dispositivos para MCMC, mas neste bloco de notas, vamos nos concentrar em duas:
- Executando cadeias de Markov independentes em diferentes dispositivos. Este caso é bastante simples e é possível fazer com vanilla TFP.
- Fragmentação de um conjunto de dados entre dispositivos. Este caso é um pouco mais complexo e requer máquinas TFP adicionadas recentemente.
Cadeias independentes
Digamos que gostaríamos de fazer inferência bayesiana em um problema usando MCMC e executar várias cadeias em paralelo em vários dispositivos (digamos, 2 em cada dispositivo). Este acaba sendo um programa que podemos apenas "mapear" entre os dispositivos, ou seja, um que não precisa de coletivos. Para garantir que cada programa execute uma cadeia de Markov diferente (em oposição a executar a mesma), passamos um valor diferente para a semente aleatória para cada dispositivo.
Vamos tentar em um problema de brinquedo de amostragem de uma distribuição gaussiana 2-D. Podemos usar a funcionalidade MCMC existente da TFP fora da caixa. Em geral, tentamos colocar a maior parte da lógica dentro de nossa função mapeada para distinguir mais explicitamente entre o que está sendo executado em todos os dispositivos e apenas no primeiro.
def run(seed):
target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob
initial_state = jnp.zeros([2, 2]) # 2 chains
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
def trace_fn(state, pkr):
return target_log_prob(state)
states, log_prob = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
kernel=kernel,
current_state=initial_state,
trace_fn=trace_fn,
seed=seed
)
return states, log_prob
Por si só, o run função leva em uma semente aleatória apátrida (para ver como apátrida trabalho aleatoriedade, você pode ler a TFP em JAX notebook ou consulte o tutorial JAX 101 ). Mapeamento run sobre diferentes sementes irá resultar na execução de várias cadeias de Markov independentes.
states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)
(8, 1000, 2, 2) (8, 1000, 2)
Observe como agora temos um eixo extra correspondendo a cada dispositivo. Podemos reorganizar as dimensões e aplainá-las para obter um eixo para as 16 correntes.
states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()
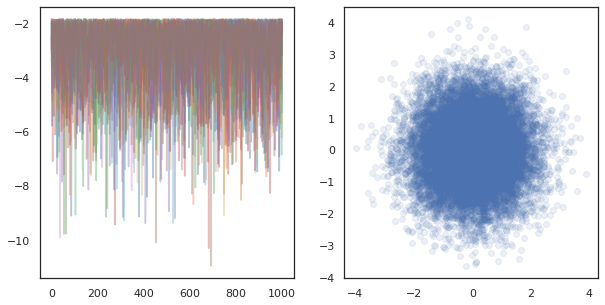
Ao executar cadeias independentes em muitos dispositivos, é tão fácil como pmap ing mais de uma função que usa tfp.mcmc , garantindo que passar valores diferentes para a semente aleatória para cada dispositivo.
Dados de fragmentação
Quando fazemos MCMC, a distribuição alvo é frequentemente uma distribuição posterior obtida pelo condicionamento em um conjunto de dados, e o cálculo de uma densidade logarítmica não normalizada envolve a soma das probabilidades de cada dado observado.
Com conjuntos de dados muito grandes, pode ser proibitivamente caro até mesmo executar uma cadeia em um único dispositivo. No entanto, quando temos acesso a vários dispositivos, podemos dividir o conjunto de dados entre os dispositivos para melhor aproveitar a computação que temos disponível.
Se gostaria de fazer MCMC com um conjunto de dados sharded, precisamos garantir a unnormalized log densidade calculamos em cada dispositivo representa o total, ou seja, a densidade sobre todos os dados, caso contrário, cada dispositivo estará fazendo MCMC com o seu próprio destino incorreto distribuição. Para este fim, a PTF tem agora novas ferramentas (ou seja tfp.experimental.distribute e tfp.experimental.mcmc ) que permitem Computing "Sharded" probabilidades de log e fazendo MCMC com eles.
Distribuições fragmentadas
A abstracção TFP núcleo proporciona agora para o cálculo de probabiliities log Sharded é o Sharded meta-distribuição, que leva uma distribuição como entrada e devolve uma nova distribuição que tem propriedades específicas, quando executado num contexto SPMD. Sharded vidas em tfp.experimental.distribute .
Intuitivamente, um Sharded corresponde distribuição para um conjunto de variáveis aleatórias que têm sido "split" entre dispositivos. Em cada dispositivo, eles produzirão diferentes amostras e podem ter diferentes log-densidades individualmente. Alternativamente, um Sharded distribuidora corresponde a uma "placa" no modelo de linguagem gráfica, onde o tamanho de placa é o número de dispositivos.
Amostragem de um Sharded distribuição
Se amostra de um Normal de distribuição em um programa ser pmap ed usando a mesma semente em cada dispositivo, teremos a mesma amostra em cada dispositivo. Podemos pensar na função a seguir como uma amostra de uma única variável aleatória que é sincronizada entre os dispositivos.
# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32)
Se nós envolvemos tfd.Normal(0., 1.) com um tfed.Sharded , que logicamente têm agora oito variáveis aleatórias diferentes (um em cada dispositivo) e, portanto, produzir uma amostra diferente para cada um, apesar passando a mesma semente .
def f(seed, _):
return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([ 1.2152631 , 0.7818249 , 0.32549605, 0.6828047 ,
1.3973192 , -0.57830244, 0.37862757, 2.7706041 ], dtype=float32)
Uma representação equivalente desta distribuição em um único dispositivo é apenas 8 amostras normais independentes. Mesmo que o valor da amostra será diferente ( tfed.Sharded faz pseudo-geração de números aleatórios de maneira ligeiramente diferente), ambos representam a mesma distribuição.
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))
DeviceArray([ 0.08086783, -0.38624594, -0.3756545 , 1.668957 ,
-1.2758069 , 2.1192007 , -0.85821325, 1.1305912 ], dtype=float32)
Tomando o log de densidade de um Sharded distribuição
Vamos ver o que acontece quando calculamos a densidade logarítmica de uma amostra de uma distribuição regular em um contexto SPMD.
def f(seed, _):
dist = tfd.Normal(0., 1.)
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32),
ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
-0.94012403, -0.94012403, -0.94012403, -0.94012403], dtype=float32))
Cada amostra é a mesma em cada dispositivo, portanto, calculamos a mesma densidade em cada dispositivo também. Intuitivamente, aqui temos apenas uma distribuição sobre uma única variável normalmente distribuída.
Com um Sharded distribuição, temos uma distribuição de mais de 8 variáveis aleatórias, então quando calculamos a log_prob de uma amostra, somamos, através de dispositivos, sobre cada um dos densidades de log individuais. (Você pode notar que este valor log_prob total é maior do que o singleton log_prob calculado acima.)
def f(seed, _):
dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)
Sample: [ 1.2152631 0.7818249 0.32549605 0.6828047 1.3973192 -0.57830244 0.37862757 2.7706041 ] Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205]
A distribuição equivalente, "não fragmentada", produz a mesma densidade de log.
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)
DeviceArray(-13.7349205, dtype=float32)
A Sharded distribuição produz valores diferentes de sample em cada dispositivo, mas obter o mesmo valor para log_prob em cada dispositivo. O que está acontecendo aqui? A Sharded distribuição faz um psum internamente para garantir os log_prob valores estão em sincronia entre dispositivos. Por que desejaríamos esse comportamento? Se nós estamos executando a mesma cadeia MCMC em cada dispositivo, gostaríamos o target_log_prob a ser o mesmo em cada dispositivo, mesmo se algumas variáveis aleatórias no cálculo são fragmentados entre dispositivos.
Além disso, um Sharded assegura uma distribuição que os gradientes em vários dispositivos são a correcta, para assegurar que os algoritmos como HMC, que tenham gradientes da função log-densidade como parte da função de transição, produzem amostras apropriadas.
Sharded JointDistribution s
Podemos criar modelos com múltiplas Sharded variáveis aleatórias usando JointDistribution s (JDs). Infelizmente, Sharded distribuições não pode ser usado com segurança com baunilha tfd.JointDistribution s, mas tfp.experimental.distribute exportações "remendado" JDs que se comportam como Sharded distribuições.
def f(seed, _):
dist = tfed.JointDistributionSequential([
tfd.Normal(0., 1.),
tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
])
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
1.6121525, 1.6121525, 1.6121525], dtype=float32),
ShardedDeviceArray([ 0.8690128 , -0.83167845, 1.2209264 , 0.88412696,
0.76478404, -0.66208494, -0.0129658 , 0.7391483 ], dtype=float32)],
ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
-12.214451, -12.214451, -12.214451, -12.214451], dtype=float32))
Estes JDs Sharded pode ter ambos Sharded distribuições e baunilha TFP como componentes. Para as distribuições não fragmentadas, obtemos a mesma amostra em cada dispositivo, e para as distribuições fragmentadas, obtemos amostras diferentes. O log_prob em cada dispositivo está sincronizado, bem.
MCMC com Sharded distribuições
Como podemos pensar em Sharded distribuições no contexto da MCMC? Se temos um modelo generativo que pode ser expressa como uma JointDistribution , podemos escolher algumas eixo desse modelo de "fragmento" de diâmetro. Normalmente, uma variável aleatória no modelo corresponderá aos dados observados e, se tivermos um grande conjunto de dados que gostaríamos de fragmentar entre os dispositivos, queremos que as variáveis associadas aos pontos de dados também sejam fragmentadas. Também podemos ter variáveis aleatórias "locais" que são um-para-um com as observações que estamos fragmentando, portanto, teremos que fragmentar adicionalmente essas variáveis aleatórias.
Nós vamos passar por cima de exemplos do uso de Sharded distribuições TFP MCMC nesta seção. Vamos começar com um exemplo de regressão logística Bayesian mais simples, e concluir com um exemplo fatoração de matriz, com o objetivo de demonstrar alguns casos de uso para o distribute biblioteca.
Exemplo: regressão logística bayesiana para MNIST
Gostaríamos de fazer regressão logística bayesiana em um grande conjunto de dados; o modelo tem um antes \(p(\theta)\) sobre os pesos de regressão, e uma probabilidade \(p(y_i | \theta, x_i)\) que é somada ao longo de todos os dados \(\{x_i, y_i\}_{i = 1}^N\) para obter a densidade de log total da articulação. Se caco nossos dados, nós caco as variáveis aleatórias observados \(x_i\) e \(y_i\) em nosso modelo.
Usamos o seguinte modelo de regressão logística Bayesiana para a classificação MNIST:
\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]
Vamos carregar o MNIST usando os conjuntos de dados TensorFlow.
mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.
raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.
Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1... WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your local data directory. If you'd instead prefer to read directly from our public GCS bucket (recommended if you're running on GCP), you can instead pass `try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`. HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio… Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.
Temos 60.000 imagens de treinamento, mas vamos aproveitar nossos 8 núcleos disponíveis e dividi-los em 8 maneiras. Usaremos este prático shard função de utilidade.
def shard_value(x):
x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices
shard = functools.partial(jax.tree_map, shard_value)
sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)
(8, 7500, 784) (8, 7500)
Antes de continuar, vamos discutir rapidamente a precisão nas TPUs e seu impacto no HMC. TPUs executar produto de matrizes usando baixo bfloat16 precisão para a velocidade. bfloat16 produto de matrizes são muitas vezes suficiente para muitas aplicações de aprendizagem profundas, mas quando usado com HMC, temos empiricamente encontrada a precisão inferior pode levar a divergência trajetórias, causando rejeições. Podemos usar multiplicações de matrizes de maior precisão, ao custo de alguns cálculos adicionais.
Para aumentar a nossa precisão matmul, podemos usar o jax.default_matmul_precision decorador com "tensorfloat32" precisão (para ainda maior precisão poderíamos usar "float32" precisão).
Vamos agora definir o nosso run função, que terá em uma semente aleatória (que será o mesmo em cada dispositivo) e um caco de MNIST. A função implementará o modelo mencionado acima e, em seguida, usaremos a funcionalidade vanilla MCMC do TFP para executar uma única cadeia. Nós vamos ter certeza de decorar run com o jax.default_matmul_precision decorador para garantir que a multiplicação de matrizes é executado com maior precisão, embora no exemplo particular abaixo, poderia muito bem usar jnp.dot(images, w, precision=lax.Precision.HIGH) .
# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device.
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
images, labels = data # a sharded dataset
num_examples, dim = images.shape
num_classes = 10
def model_fn():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
logits = jnp.dot(images, w) + b
yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
shard_axis_name='data')
model = tfed.JointDistributionCoroutine(model_fn)
init_seed, sample_seed = random.split(seed)
initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`
def target_log_prob(*state):
return model.log_prob((*state, labels))
def accuracy(w, b):
logits = images.dot(w) + b
preds = logits.argmax(axis=-1)
# We take the average accuracy across devices by using `lax.pmean`
return lax.pmean((preds == labels).mean(), 'data')
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
def trace_fn(state, pkr):
return (
target_log_prob(*state),
accuracy(*state),
pkr.new_step_size)
states, trace = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
current_state=initial_state,
kernel=kernel,
trace_fn=trace_fn,
seed=sample_seed
)
return states, trace
jax.pmap inclui uma compilação JIT mas a função compilado é armazenado em cache após a primeira chamada. Vamos chamar run e ignorar a saída para armazenar em cache a compilação.
%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)
CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s Wall time: 1min 54s
Vamos agora chamar run novamente para ver quanto tempo a execução real leva.
%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)
CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s Wall time: 1min 43s
Estamos executando 200.000 etapas de salto, cada uma das quais calcula um gradiente em todo o conjunto de dados. Dividir a computação em 8 núcleos nos permite calcular o equivalente a 200.000 épocas de treinamento em cerca de 95 segundos, cerca de 2.100 épocas por segundo!
Vamos plotar a densidade logarítmica de cada amostra e a precisão de cada amostra:
fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()
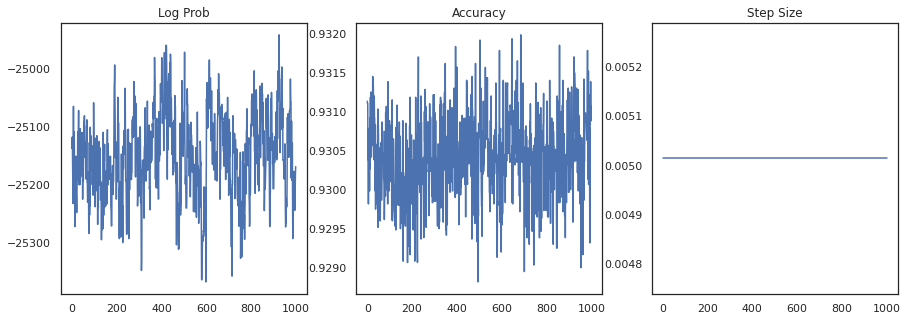
Se juntarmos as amostras, podemos calcular a média do modelo bayesiano para melhorar nosso desempenho.
@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
images, labels = data
logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
probs = jax.nn.softmax(logits, axis=-1)
bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')
sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')
Average Accuracy: 0.9188529253005981 BMA Accuracy: 0.9264000058174133 Accuracy Improvement: 0.0075470805168151855
A média do modelo Bayesiano aumenta nossa precisão em quase 1%!
Exemplo: sistema de recomendação MovieLens
Agora vamos tentar fazer inferências com o conjunto de dados de recomendações do MovieLens, que é uma coleção de usuários e suas classificações de vários filmes. Especificamente, podemos representar MovieLens como um \(N \times M\) matriz relógio \(W\) onde \(N\) é o número de usuários e \(M\) é o número de filmes; esperamos \(N > M\). As entradas de \(W_{ij}\) são um booleano que indica se ou não usuário \(i\) assistiu filme \(j\). Observe que o MovieLens fornece classificações de usuários, mas as estamos ignorando para simplificar o problema.
Primeiro, vamos carregar o conjunto de dados. Usaremos a versão com 1 milhão de avaliações.
movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']
Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0... HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl… HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value=''))) Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value=''))) Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.
Nós vamos fazer alguns pré-processamento do conjunto de dados para obter a matriz relógio \(W\).
raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']
movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])
num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1
movie_titles = dict(zip(movielens['train']['movie_id'],
movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]
watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)
(6040, 3706)
Podemos definir um modelo generativo para \(W\), utilizando um modelo de fatoração de matriz probabilística simples. Assumimos uma latente \(N \times D\) matriz usuário \(U\) e uma latente \(M \times D\) matriz filme \(V\), que quando multiplicado produzir os logits de Bernoulli para a matriz relógio \(W\). Também vamos incluir um vetores viés para usuários e filmes, \(u\) e \(v\).
\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]
Esta é uma matriz muito grande; 6.040 usuários e 3.706 filmes levam a uma matriz com mais de 22 milhões de entradas. Como abordamos a fragmentação deste modelo? Bem, se assumirmos que \(N > M\) (ou seja, há mais usuários do que os filmes), então não faria sentido para caco matriz relógio ao longo do eixo do usuário, de modo que cada dispositivo teria um pedaço de matriz relógio que corresponde a um subconjunto de usuários . Ao contrário do exemplo anterior, no entanto, que vai igualmente ter a fragmentar-se o \(U\) matriz, uma vez que tem uma incorporação para cada utilizador, de modo que cada dispositivo será responsável por um fragmento de \(U\) e um fragmento de \(W\). Por outro lado, \(V\) será unsharded e serem sincronizados através de dispositivos.
sharded_watch_matrix = shard(watch_matrix)
Antes de escrever o nosso run , vamos discutir rapidamente os desafios adicionais com sharding a variável aleatória locais \(U\). Ao executar HMC, a baunilha tfp.mcmc.HamiltonianMonteCarlo kernel irá experimentar momentos para cada elemento de estado da cadeia. Anteriormente, apenas variáveis aleatórias não fragmentadas faziam parte desse estado, e os momentos eram os mesmos em cada dispositivo. Quando temos agora uma sharded \(U\), precisamos provar momentos diferentes em cada dispositivo para \(U\), enquanto experimenta o mesmo momentos para \(V\). Para conseguir isso, podemos usar tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo com um Sharded distribuição de momentum. À medida que continuamos a tornar a computação paralela de primeira classe, podemos simplificar isso, por exemplo, levando um indicador de fragmentação para o kernel do HMC.
def make_run(*,
axis_name,
dim=20,
num_chains=2,
prior_variance=1.,
step_size=1e-2,
num_leapfrog_steps=100,
num_burnin_steps=1000,
num_results=500,
):
@functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
@jax.default_matmul_precision('tensorfloat32')
def run(key, watch_matrix):
num_users, num_movies = watch_matrix.shape
Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)
def prior_fn():
user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
return (user_embeddings, user_bias, movie_embeddings, movie_bias)
prior = tfed.JointDistributionCoroutine(prior_fn)
def model_fn():
user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
+ user_bias[..., :, None] + movie_bias[..., None, :])
yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
model = tfed.JointDistributionCoroutine(model_fn)
init_key, sample_key = random.split(key)
initial_state = prior.sample(seed=init_key, sample_shape=num_chains)
def target_log_prob(*state):
return model.log_prob((*state, watch_matrix))
momentum_distribution = tfed.JointDistributionSequential([
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
])
# We pass in momentum_distribution here to ensure that the momenta for
# user_embeddings and user_bias are also sharded
kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
num_leapfrog_steps,
momentum_distribution=momentum_distribution)
num_adaptation_steps = int(0.8 * num_burnin_steps)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)
def trace_fn(state, pkr):
return {
'log_prob': target_log_prob(*state),
'log_accept_ratio': pkr.inner_results.log_accept_ratio,
}
return tfm.sample_chain(
num_results, initial_state,
kernel=kernel,
num_burnin_steps=num_burnin_steps,
trace_fn=trace_fn,
seed=sample_key)
return run
Nós novamente vai executá-lo uma vez para armazenar em cache o compilado run .
%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)
CPU times: user 56 s, sys: 1min 24s, total: 2min 20s Wall time: 3min 35s
Agora vamos executá-lo novamente sem o overhead de compilação.
%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)
CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s Wall time: 3min 1s
Parece que completamos cerca de 150.000 passos de salto em cerca de 3 minutos, então cerca de 83 passos de salto de sapo por segundo! Vamos representar graficamente a razão de aceitação e a densidade logarítmica de nossas amostras.
fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
ax.plot(val[0]) # Indexing into a sharded array, each element is the same
ax.set_title(key);
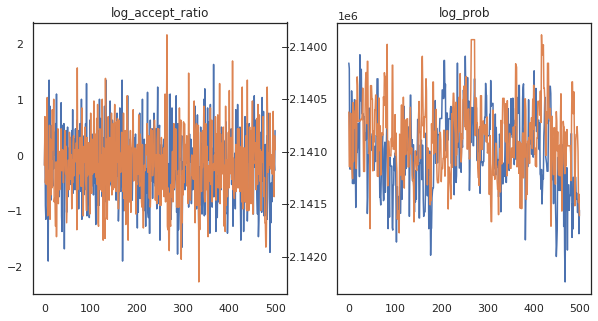
Agora que temos algumas amostras de nossa cadeia de Markov, vamos usá-las para fazer algumas previsões. Primeiro, vamos extrair cada um dos componentes. Lembre-se que os user_embeddings e user_bias estão divididos em dispositivo, por isso precisamos concatenar nosso ShardedArray obter todos eles. Por outro lado, movie_embeddings e movie_bias são os mesmos em todos os dispositivos, para que possamos escolher apenas o valor do primeiro fragmento. Usaremos regulares numpy para copiar os valores da parte de trás TPUs a CPU.
user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')
User embeddings: (500, 2, 6040, 20) User bias: (500, 2, 6040) Movie embeddings: (500, 2, 3706, 20) Movie bias: (500, 2, 3706)
Vamos tentar construir um sistema de recomendação simples que utilize a incerteza capturada nessas amostras. Vamos primeiro escrever uma função que classifica os filmes de acordo com a probabilidade de assistir.
@jax.jit
def recommend(sample, user_id):
user_embeddings, user_bias, movie_embeddings, movie_bias = sample
movie_logits = (
jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
+ user_bias[user_id] + movie_bias)
return movie_logits.argsort()[::-1]
Agora podemos escrever uma função que percorre todas as amostras e, para cada uma, escolhe o filme mais bem classificado que o usuário ainda não assistiu. Podemos então ver a contagem de todos os filmes recomendados nas amostras.
def get_recommendations(user_id):
movie_ids = []
already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
for i in range(500):
for j in range(2):
sample = jax.tree_map(lambda x: x[i, j], samples)
ranking = recommend(sample, user_id)
for movie_id in ranking:
if int(movie_id) not in already_watched:
movie_ids.append(movie_id)
break
return movie_ids
def plot_recommendations(movie_ids, ax=None):
titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
ax = ax or plt.gca()
names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
ax.bar(names, counts)
ax.set_xticklabels(names, rotation=90)
Vamos pegar o usuário que viu mais filmes e o que viu menos.
user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])
2314 20
Esperamos que o nosso sistema tem mais certeza sobre user_most que user_least , uma vez que temos mais informações sobre que tipos de filmes user_most é mais provável para assistir.
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');
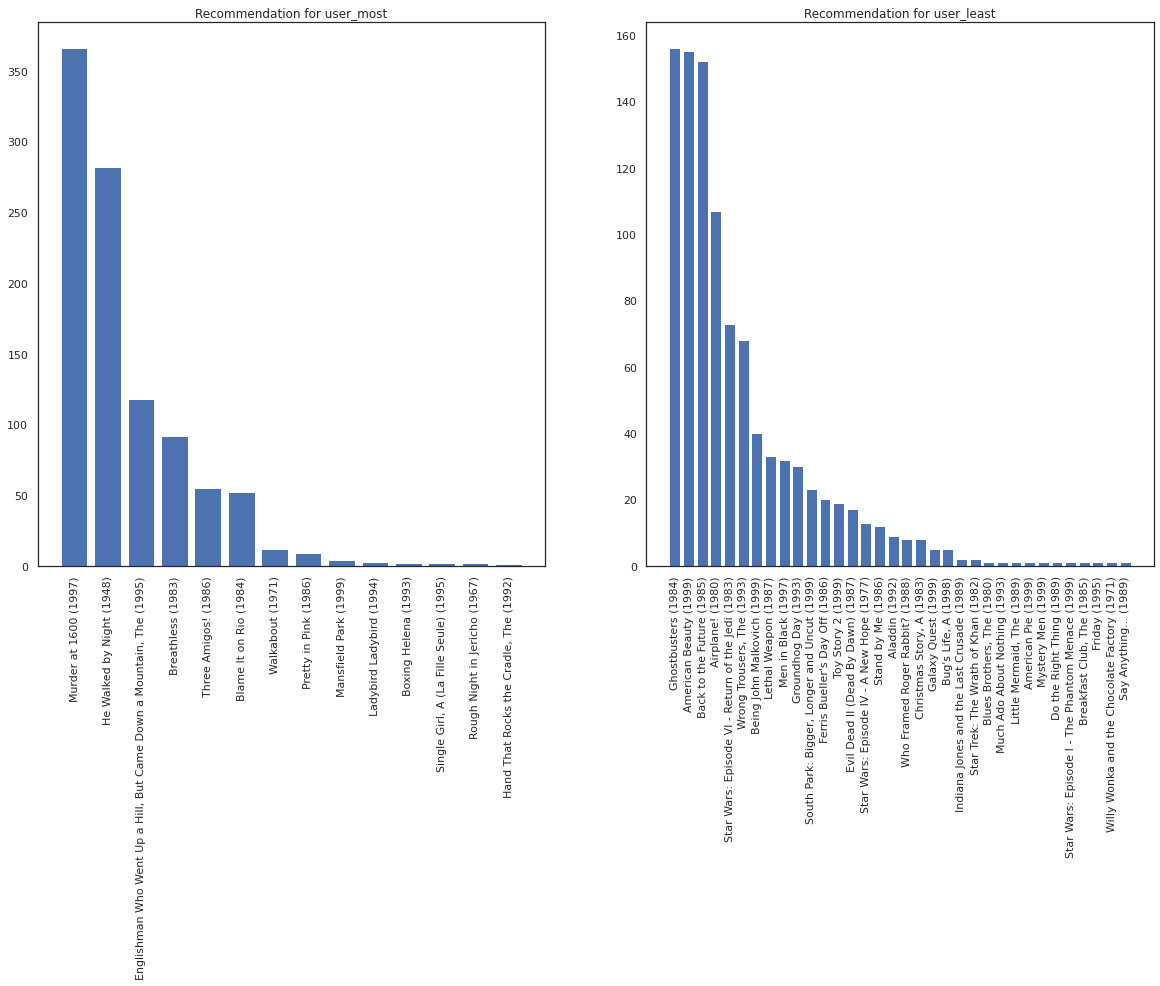
Vemos que há mais variância em nossas recomendações para user_least refletindo nossa incerteza adicional em suas preferências relógio.
Também podemos ver os gêneros dos filmes recomendados.
most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');
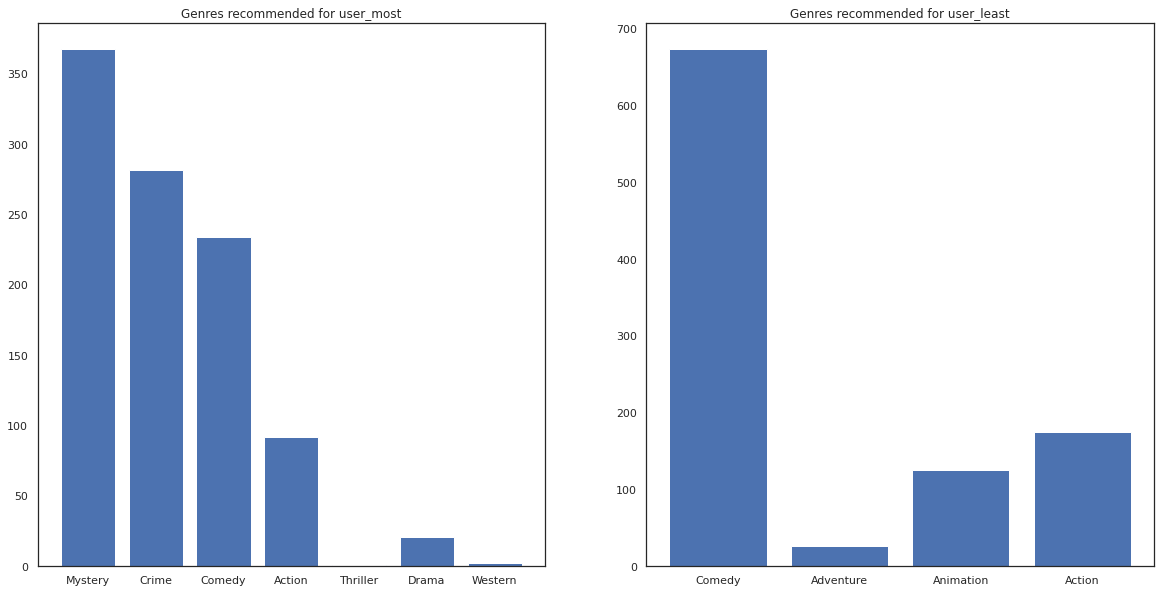
user_most viu um monte de filmes e tem sido recomendado mais gêneros de nicho como mistério e crime enquanto user_least não assistiu a muitos filmes e foi recomendado mais filmes tradicionais, que comédia de inclinação e ação.
