Visualizza su TensorFlow.org

Esegui in Google Colab

Visualizza la fonte su GitHub

Scarica taccuino

TensorFlow Probability (TFP) su JAX ora dispone di strumenti per il calcolo numerico distribuito. Per scalare a un numero elevato di acceleratori, gli strumenti sono basati sulla scrittura di codice utilizzando il paradigma "programma multiplo a programma singolo", o SPMD in breve.

In questo notebook, esamineremo come "pensare in SPMD" e introdurremo le nuove astrazioni TFP per il ridimensionamento a configurazioni come pod TPU o cluster di GPU. Se esegui tu stesso questo codice, assicurati di selezionare un runtime TPU.

Per prima cosa installeremo le ultime versioni TFP, JAX e TF.

Installa

pip install jaxlib --upgrade -q 2>&1 1> /dev/null
pip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/null
pip install tf-nightly-cpu -q -I 2>&1 1> /dev/null
pip install jax -I -q --upgrade 2>&1 1>/dev/null

Importeremo alcune librerie generali, insieme ad alcune utilità JAX.

Configurazione e importazioni

import functools
import collections
import contextlib

import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds

from tensorflow_probability.substrates import jax as tfp

sns.set(style='white')

INFO:tensorflow:Enabling eager execution
INFO:tensorflow:Enabling v2 tensorshape
INFO:tensorflow:Enabling resource variables
INFO:tensorflow:Enabling tensor equality
INFO:tensorflow:Enabling control flow v2

Verranno inoltre impostati alcuni utili alias TFP. Le nuove astrazioni sono attualmente forniti in tfp.experimental.distribute e tfp.experimental.mcmc .

tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc

Root = tfed.JointDistributionCoroutine.Root

Per collegare il notebook a un TPU, utilizziamo il seguente helper di JAX. Per confermare che siamo connessi, stampiamo il numero di dispositivi, che dovrebbe essere otto.

from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')

Found 8 devices

Una rapida introduzione al jax.pmap

Volta collegato ad un TPU, abbiamo accesso a otto dispositivi. Tuttavia, quando eseguiamo il codice JAX con entusiasmo, JAX per impostazione predefinita esegue i calcoli su uno solo.

Il modo più semplice per eseguire un calcolo su molti dispositivi è mappare una funzione, facendo eseguire a ciascun dispositivo un indice della mappa. JAX fornisce il jax.pmap ( "mappa parallelo") trasformazione che trasforma una funzione in una che mappa la funzione tramite vari dispositivi.

Nell'esempio seguente, creiamo un array di dimensione 8 (in modo che corrisponda al numero di dispositivi disponibili) e mappiamo una funzione che ne aggiunge 5.

xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)

<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5.  6.  7.  8.  9. 10. 11. 12.]

Nota di ricezione di ShardedDeviceArray tipo indietro, indicando che l'array di uscita è fisicamente divisa tra dispositivi.

jax.pmap agisce semanticamente come una mappa, ma ha alcune importanti opzioni che modificano il comportamento. Per default, pmap assume tutti gli ingressi alla funzione vengono mappati sopra, ma può modificare questo comportamento con in_axes argomento.

xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)

[ 5.  6.  7.  8.  9. 10. 11. 12.]

Analogamente, il out_axes argomento pmap determina se restituire i valori su ogni dispositivo. Impostazione out_axes a None restituisce automaticamente il valore al 1 ° dispositivo e devono essere utilizzati solo se siamo certi che i valori sono gli stessi su tutti i dispositivi.

xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)

2.0

Cosa succede quando ciò che vorremmo fare non è facilmente esprimibile come una pura funzione mappata? Ad esempio, cosa succede se volessimo fare una somma attraverso l'asse su cui stiamo mappando? JAX offre "collettivi", funzioni che comunicano tra dispositivi, per consentire la scrittura di programmi distribuiti più interessanti e complessi. Per capire come funzionano esattamente, introdurremo SPMD.

Cos'è SPMD?

Single-program multiple-data (SPMD) è un modello di programmazione simultanea in cui un singolo programma (cioè lo stesso codice) viene eseguito simultaneamente su più dispositivi, ma gli input per ciascuno dei programmi in esecuzione possono essere diversi.

Se il nostro programma è una semplice funzione dei suoi ingressi (vale a dire qualcosa come x + 5 ), in esecuzione di un programma in SPMD è solo mappandola di dati su diverse, come abbiamo fatto con jax.pmap in precedenza. Tuttavia, possiamo fare di più che "mappare" una funzione. JAX offre "collettivi", che sono funzioni che comunicano tra dispositivi.

Ad esempio, forse vorremmo prendere la somma di una quantità su tutti i nostri dispositivi. Prima di farlo, abbiamo bisogno di assegnare un nome al abbiamo all'asse stiamo mappando sopra nel pmap . Abbiamo poi utilizziamo il lax.psum funzione ( "sum parallelo") per eseguire una somma tra i dispositivi, garantendo identifichiamo il nome dell'asse stiamo sommando su.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)

ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)

Il psum aggregati collettivi il valore di x di ciascun dispositivo e sincronizza il suo valore di tutti i cartina cioè out è 28. su ogni dispositivo. Non stiamo più eseguendo una semplice "mappa", ma stiamo eseguendo un programma SPMD in cui il calcolo di ogni dispositivo può ora interagire con lo stesso calcolo su altri dispositivi, anche se in modo limitato utilizzando i collettivi. In questo scenario, possiamo usare out_axes = None , perché psum si sincronizzerà il valore.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))

ShardedDeviceArray(28., dtype=float32)

SPMD ci consente di scrivere un programma che viene eseguito su ogni dispositivo in qualsiasi configurazione TPU contemporaneamente. Lo stesso codice utilizzato per eseguire l'apprendimento automatico su 8 core TPU può essere utilizzato su un pod TPU che può avere da centinaia a migliaia di core! Per un tutorial più dettagliate circa jax.pmap e SPMD, è possibile fare riferimento al il JAX 101 esercitazione .

MCMC su larga scala

In questo taccuino, ci concentriamo sull'uso dei metodi Markov Chain Monte Carlo (MCMC) per l'inferenza bayesiana. Ci sono molti modi in cui utilizziamo molti dispositivi per MCMC, ma in questo notebook ci concentreremo su due:

1. Esecuzione di catene Markov indipendenti su dispositivi diversi. Questo caso è abbastanza semplice ed è possibile farlo con Vanilla TFP.
2. Sharding di un set di dati tra dispositivi. Questo caso è un po' più complesso e richiede macchinari TFP aggiunti di recente.

Catene Indipendenti

Supponiamo che vorremmo eseguire l'inferenza bayesiana su un problema utilizzando MCMC e vorremmo eseguire diverse catene in parallelo su più dispositivi (diciamo 2 su ciascun dispositivo). Questo risulta essere un programma che possiamo semplicemente "mappare" tra i dispositivi, cioè uno che non ha bisogno di collettivi. Per assicurarci che ogni programma esegua una catena Markov diversa (invece di eseguire la stessa), passiamo un valore diverso per il seme casuale a ciascun dispositivo.

Proviamolo su un problema giocattolo di campionamento da una distribuzione gaussiana 2-D. Possiamo utilizzare la funzionalità MCMC esistente di TFP pronta all'uso. In generale, cerchiamo di inserire la maggior parte della logica all'interno della nostra funzione mappata per distinguere in modo più esplicito tra ciò che è in esecuzione su tutti i dispositivi rispetto solo al primo.

def run(seed):
  target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob

  initial_state = jnp.zeros([2, 2]) # 2 chains
  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
  def trace_fn(state, pkr):
    return target_log_prob(state)

  states, log_prob = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    kernel=kernel,
    current_state=initial_state,
    trace_fn=trace_fn,
    seed=seed
  )
  return states, log_prob

Di per sé, la run funzione prende in un seme casuale senza stato (per vedere come apolidi lavoro casualità, è possibile leggere il TFP su JAX notebook o vedere il tutorial di JAX 101 ). Mappatura run su diversi semi si tradurrà in esecuzione diverse catene indipendenti di Markov.

states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)

(8, 1000, 2, 2) (8, 1000, 2)

Nota come ora abbiamo un asse in più corrispondente a ciascun dispositivo. Possiamo riordinare le dimensioni e appiattirle per ottenere un asse per le 16 catene.

states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])

fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()

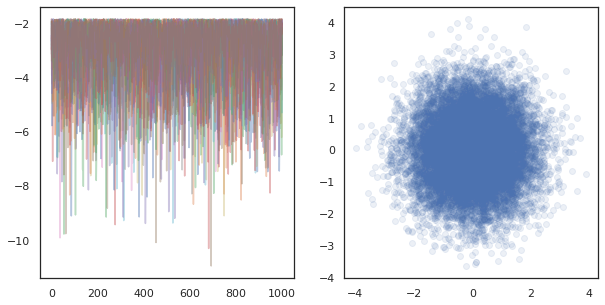
Quando si esegue catene indipendenti su molti dispositivi, è facile come pmap -ing su una funzione che usi tfp.mcmc , assicurando passiamo valori diversi per il seme casuale per ciascun dispositivo.

Sharding dei dati

Quando eseguiamo MCMC, la distribuzione target è spesso una distribuzione a posteriori ottenuta condizionando un set di dati e il calcolo di una densità logaritmica non normalizzata implica la somma delle probabilità per ciascun dato osservato.

Con set di dati molto grandi, può essere proibitivo anche eseguire una catena su un singolo dispositivo. Tuttavia, quando abbiamo accesso a più dispositivi, possiamo suddividere il set di dati tra i dispositivi per sfruttare meglio il calcolo che abbiamo a disposizione.

Se vorremmo fare MCMC con un set di dati sharded, dobbiamo garantire la non normalizzato log densità si calcola su ogni dispositivo rappresenta il totale, vale a dire la densità su tutti i dati, altrimenti ogni dispositivo farà MCMC con la propria destinazione errato distribuzione. A tal fine, la TFP ha ora nuovi strumenti (ad esempio tfp.experimental.distribute e tfp.experimental.mcmc ), che permetterà di calcolo delle probabilità del registro "sharded" e facendo MCMC con loro.

Distribuzioni frammentate

L'astrazione TFP nucleo fornisce ora per calcolare probabiliities registro sharded rappresenta l' Sharded meta-distribuzione, che richiede una distribuzione come input e restituisce una nuova distribuzione che ha proprietà specifiche quando eseguito in un contesto SPMD. Sharded vive in tfp.experimental.distribute .

Intuitivamente, un Sharded corrisponde distribuzione di un insieme di variabili casuali che sono stati "split" tra i dispositivi. Su ogni dispositivo, produrranno campioni diversi e possono avere individualmente densità di registro diverse. In alternativa, un Sharded corrisponde ad una distribuzione "piatto" in gergo modello grafica, dove le dimensioni della lastra è il numero di dispositivi.

Campionamento uno Sharded di distribuzione

Se ci campione da una Normal distribuzione in un programma di essere pmap -ed utilizzando lo stesso seme su ogni dispositivo, avremo lo stesso campione su ogni dispositivo. Possiamo pensare alla seguente funzione come al campionamento di una singola variabile casuale sincronizzata tra i dispositivi.

# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
  return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                    -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32)

Se ci avvolgono tfd.Normal(0., 1.) con un tfed.Sharded , abbiamo logicamente ora abbiamo otto diverse variabili casuali (uno su ciascun dispositivo) e pertanto produrre un campione diverso per ognuno, pur superando nello stesso seme .

def f(seed, _):
  return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([ 1.2152631 ,  0.7818249 ,  0.32549605,  0.6828047 ,
                     1.3973192 , -0.57830244,  0.37862757,  2.7706041 ],                   dtype=float32)

Una rappresentazione equivalente di questa distribuzione su un singolo dispositivo è solo un 8 campioni normali indipendenti. Anche se il valore del campione sarà diverso ( tfed.Sharded fa pseudo-casuali generazione di numeri leggermente diverso), entrambi rappresentano la stessa distribuzione.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))

DeviceArray([ 0.08086783, -0.38624594, -0.3756545 ,  1.668957  ,
             -1.2758069 ,  2.1192007 , -0.85821325,  1.1305912 ],            dtype=float32)

Prendendo il log-densità di uno Sharded di distribuzione

Vediamo cosa succede quando calcoliamo la densità log di un campione da una distribuzione regolare in un contesto SPMD.

def f(seed, _):
  dist = tfd.Normal(0., 1.)
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                     -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32),
 ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
                     -0.94012403, -0.94012403, -0.94012403, -0.94012403],                   dtype=float32))

Ogni campione è lo stesso su ogni dispositivo, quindi calcoliamo la stessa densità anche su ogni dispositivo. Intuitivamente, qui abbiamo solo una distribuzione su una singola variabile distribuita normalmente.

Con uno Sharded distribuzione, abbiamo una distribuzione su 8 variabili casuali, in modo che quando si calcola il log_prob di un campione, si somma, su tutti i dispositivi, su ciascuno dei singoli densità di registro. (Potresti notare che questo valore totale log_prob è maggiore del singleton log_prob calcolato sopra.)

def f(seed, _):
  dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
    random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)

Sample: [ 1.2152631   0.7818249   0.32549605  0.6828047   1.3973192  -0.57830244
  0.37862757  2.7706041 ]
Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205
 -13.7349205 -13.7349205]

La distribuzione equivalente, "unsharded" produce la stessa densità di log.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)

DeviceArray(-13.7349205, dtype=float32)

Uno Sharded distribuzione produce valori diversi da sample su ciascun dispositivo, ma ottenere lo stesso valore per log_prob su ogni dispositivo. Cosa sta succedendo qui? Uno Sharded distribuzione fa un psum internamente per garantire i log_prob valori sono sincronizzati tra dispositivi. Perché dovremmo volere questo comportamento? Se stiamo eseguendo la stessa catena MCMC su ogni dispositivo, vorremmo il target_log_prob per essere lo stesso su ogni dispositivo, anche se alcune variabili aleatorie nel calcolo sono sharded su più dispositivi.

Inoltre, un Sharded assicura una distribuzione che gradienti su dispositivi al corretto, per garantire che algoritmi come HMC, che prendono gradienti della funzione log densità come parte della funzione di transizione, producono campioni adeguati.

Sharded JointDistribution s

Siamo in grado di creare modelli con più Sharded variabili casuali utilizzando JointDistribution s (JDs). Purtroppo, Sharded distribuzioni non possono essere utilizzate in modo sicuro con vaniglia tfd.JointDistribution s, ma tfp.experimental.distribute esportazioni "patchati" JDs che si comporterà come Sharded distribuzioni.

def f(seed, _):
  dist = tfed.JointDistributionSequential([
    tfd.Normal(0., 1.),
    tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
  ])
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
                      1.6121525, 1.6121525, 1.6121525], dtype=float32),
  ShardedDeviceArray([ 0.8690128 , -0.83167845,  1.2209264 ,  0.88412696,
                       0.76478404, -0.66208494, -0.0129658 ,  0.7391483 ],                   dtype=float32)],
 ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
                     -12.214451, -12.214451, -12.214451, -12.214451],                   dtype=float32))

Questi JDs sharded possono avere sia Sharded distribuzioni e vaniglia TFP come componenti. Per le distribuzioni non sharded, otteniamo lo stesso campione su ogni dispositivo e per le distribuzioni sharded, otteniamo campioni diversi. La log_prob su ogni dispositivo viene sincronizzato pure.

MCMC con Sharded distribuzioni

Come pensiamo Sharded distribuzioni nel contesto della MCMC? Se abbiamo un modello generativo che può essere espressa come JointDistribution , siamo in grado di scegliere alcuni assi di quel modello di "frammento" di diametro. In genere, una variabile casuale nel modello corrisponderà ai dati osservati e, se disponiamo di un set di dati di grandi dimensioni che vorremmo suddividere tra i dispositivi, vogliamo che anche le variabili associate ai punti dati vengano partizionate. Potremmo anche avere variabili casuali "locali" che sono uno a uno con le osservazioni che stiamo dividendo, quindi dovremo frazionare ulteriormente quelle variabili casuali.

Andremo su esempi di utilizzo di Sharded distribuzioni con TFP MCMC in questa sezione. Inizieremo con un esempio di regressione logistica Bayesiano più semplice, e concludere con un esempio di matrice di fattorizzazione, con l'obiettivo di dimostrare alcuni casi d'uso per l' distribute biblioteca.

Esempio: regressione logistica bayesiana per MNIST

Ci piacerebbe fare una regressione logistica bayesiana su un grande set di dati; il modello ha una prima \(p(\theta)\) sui pesi di regressione, e un rischio \(p(y_i | \theta, x_i)\) che viene sommato per tutti i dati \(\{x_i, y_i\}_{i = 1}^N\) per ottenere la densità registro articolare. Se Shard i nostri dati, avremmo Shard le variabili casuali osservati \(x_i\) e \(y_i\) nel nostro modello.

Usiamo il seguente modello di regressione logistica bayesiana per la classificazione MNIST:

\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]

Carichiamo MNIST utilizzando i set di dati TensorFlow.

mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.

raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.

Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1...
WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your
local data directory. If you'd instead prefer to read directly from our public
GCS bucket (recommended if you're running on GCP), you can instead pass
`try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`.
HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio…
Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.

Abbiamo 60000 immagini di addestramento ma approfittiamo dei nostri 8 core disponibili e dividiamoli in 8 modi. Useremo questo pratico shard funzione di utilità.

def shard_value(x):
  x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
  return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices

shard = functools.partial(jax.tree_map, shard_value)

sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)

(8, 7500, 784) (8, 7500)

Prima di continuare, discutiamo rapidamente della precisione sui TPU e del suo impatto su HMC. TPU eseguire moltiplicazione di matrici utilizzando partire bfloat16 precisione per la velocità. bfloat16 moltiplicazione di matrici sono spesso sufficienti per molte applicazioni di apprendimento profonde, ma quando viene utilizzato con HMC, abbiamo trovato empiricamente la precisione inferiore può portare a divergenti traiettorie, causando rifiuti. Possiamo usare moltiplicazioni di matrici di maggiore precisione, al costo di qualche calcolo aggiuntivo.

Per aumentare la nostra precisione matmul, possiamo usare il jax.default_matmul_precision decoratore con "tensorfloat32" di precisione (per la precisione ancora più elevata potremmo usare "float32" precisione).

Definiamo la nostra run funzione, che avrà in un seme casuale (che sarà lo stesso su ogni dispositivo) e un frammento di MNIST. La funzione implementerà il modello di cui sopra e utilizzeremo quindi la funzionalità MCMC vanilla di TFP per eseguire una singola catena. Faremo in modo di decorare run con la jax.default_matmul_precision decoratrice per assicurarsi che la moltiplicazione di matrici viene eseguito con una precisione più elevata, anche se in particolare esempio di seguito, potremmo anche utilizzare jnp.dot(images, w, precision=lax.Precision.HIGH) .

# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device. 
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
  images, labels = data # a sharded dataset
  num_examples, dim = images.shape
  num_classes = 10

  def model_fn():
    w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
    b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
    logits = jnp.dot(images, w) + b
    yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
                       shard_axis_name='data')
  model = tfed.JointDistributionCoroutine(model_fn)

  init_seed, sample_seed = random.split(seed)

  initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`

  def target_log_prob(*state):
    return model.log_prob((*state, labels))

  def accuracy(w, b):
    logits = images.dot(w) + b
    preds = logits.argmax(axis=-1)
    # We take the average accuracy across devices by using `lax.pmean`
    return lax.pmean((preds == labels).mean(), 'data')

  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
  kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
  def trace_fn(state, pkr):
    return (
        target_log_prob(*state),
        accuracy(*state),
        pkr.new_step_size)
  states, trace = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    current_state=initial_state,
    kernel=kernel,
    trace_fn=trace_fn,
    seed=sample_seed
  )
  return states, trace

jax.pmap include una compilazione JIT ma la funzione compilato viene memorizzato nella cache dopo la prima chiamata. Chiameremo run e ignoriamo l'uscita di memorizzare nella cache la compilazione.

%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s
Wall time: 1min 54s

Noi ora chiamiamo run di nuovo per vedere quanto tempo l'effettiva esecuzione prende.

%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s
Wall time: 1min 43s

Stiamo eseguendo 200.000 passaggi di scavalcamento, ognuno dei quali calcola un gradiente sull'intero set di dati. La suddivisione del calcolo su 8 core ci consente di calcolare l'equivalente di 200.000 epoche di addestramento in circa 95 secondi, circa 2.100 epoche al secondo!

Tracciamo la densità logaritmica di ogni campione e l'accuratezza di ogni campione:

fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()

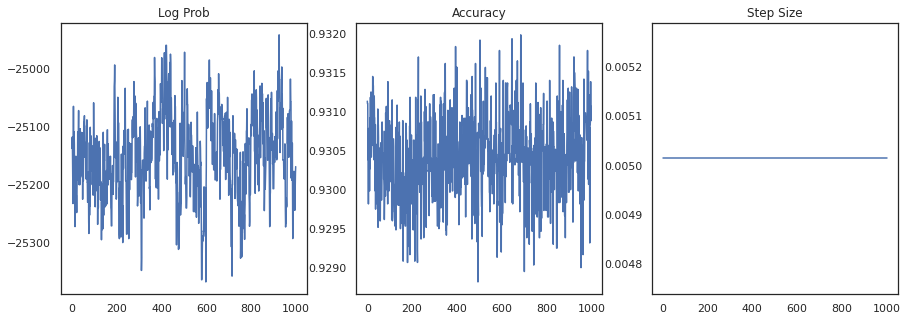
Se uniamo i campioni, possiamo calcolare una media del modello bayesiano per migliorare le nostre prestazioni.

@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
  images, labels = data
  logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
  probs = jax.nn.softmax(logits, axis=-1)
  bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
  avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
  return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')

sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')

Average Accuracy: 0.9188529253005981
BMA Accuracy: 0.9264000058174133
Accuracy Improvement: 0.0075470805168151855

Una media del modello bayesiano aumenta la nostra precisione di quasi l'1%!

Esempio: sistema di suggerimenti MovieLens

Proviamo ora a fare un'inferenza con il set di dati dei consigli di MovieLens, che è una raccolta di utenti e le loro valutazioni di vari film. Specificamente, possiamo rappresentare MovieLens come un \(N \times M\) matrice watch \(W\) dove \(N\) è il numero di utenti e \(M\) è il numero di film; ci aspettiamo \(N > M\). Le voci di \(W_{ij}\) sono un valore booleano che indica se o meno utenti \(i\) guardato film \(j\). Nota che MovieLens fornisce le valutazioni degli utenti, ma le ignoriamo per semplificare il problema.

Per prima cosa, caricheremo il set di dati. Useremo la versione con 1 milione di voti.

movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
          'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
          'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
          'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']

Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0...
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl…

HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value='')))
Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord
HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value='')))
Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.

Faremo un po 'di pre-elaborazione del set di dati per ottenere la matrice orologio \(W\).

raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']

movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])

num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1

movie_titles = dict(zip(movielens['train']['movie_id'],
                        movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
                        genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
                     for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]

watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)

(6040, 3706)

Possiamo definire un modello generativa per \(W\), utilizzando un semplice modello fattorizzazione matrice probabilistico. Si ipotizza un latente \(N \times D\) matrice dell'utente \(U\) e un latente \(M \times D\) matrice film \(V\), che moltiplicato produce i logit di Bernoulli per la matrice orologio \(W\). Includeremo anche un vettori di polarizzazione per gli utenti e film, \(u\) e \(v\).

\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]

Questa è una matrice piuttosto grande; 6040 utenti e 3706 filmati portano a una matrice con oltre 22 milioni di voci al suo interno. Come ci avviciniamo alla sharding di questo modello? Ebbene, se assumiamo che \(N > M\) (cioè ci sono più utenti di film), allora avrebbe senso coccio matrice orologio attraverso l'asse utente, quindi ogni dispositivo avrebbe un pezzo di matrice orologio corrispondente ad un sottoinsieme di utenti . A differenza dell'esempio precedente, tuttavia, dovremo anche coccio il \(U\) matrice, in quanto ha un'immersione per ciascun utente, in modo che ogni dispositivo sarà responsabile di un frammento di \(U\) e un frammento di \(W\). D'altra parte, \(V\) sarà unsharded e essere sincronizzati tra dispositivi.

sharded_watch_matrix = shard(watch_matrix)

Prima di scrivere la nostra run , proviamo ad esaminare rapidamente le sfide supplementari con sharding la variabile casuale locale \(U\). Quando si esegue HMC, la vaniglia tfp.mcmc.HamiltonianMonteCarlo momenti kernel sarà campione per ogni elemento dello stato della catena. In precedenza, solo le variabili casuali unsharded facevano parte di quello stato e i momenti erano gli stessi su ogni dispositivo. Quando ora abbiamo una sharded \(U\), dobbiamo campionare momenti differenti su ogni dispositivo per \(U\), mentre il campionamento la stessa quantità di moto per \(V\). Per fare questo, possiamo usare tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo con uno Sharded distribuzione del momento. Poiché continuiamo a rendere il calcolo parallelo di prima classe, possiamo semplificarlo, ad esempio portando un indicatore di shardedness al kernel HMC.

def make_run(*,
             axis_name,
             dim=20,
             num_chains=2,
             prior_variance=1.,
             step_size=1e-2,
             num_leapfrog_steps=100,
             num_burnin_steps=1000,
             num_results=500,
             ):
  @functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
  @jax.default_matmul_precision('tensorfloat32')
  def run(key, watch_matrix):
    num_users, num_movies = watch_matrix.shape

    Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)

    def prior_fn():
      user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
      user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
      movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
      movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
      return (user_embeddings, user_bias, movie_embeddings, movie_bias)
    prior = tfed.JointDistributionCoroutine(prior_fn)

    def model_fn():
      user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
      logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
                + user_bias[..., :, None] + movie_bias[..., None, :])
      yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
    model = tfed.JointDistributionCoroutine(model_fn)

    init_key, sample_key = random.split(key)
    initial_state = prior.sample(seed=init_key, sample_shape=num_chains)

    def target_log_prob(*state):
      return model.log_prob((*state, watch_matrix))

    momentum_distribution = tfed.JointDistributionSequential([
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
    ])

    # We pass in momentum_distribution here to ensure that the momenta for 
    # user_embeddings and user_bias are also sharded
    kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
                                                      num_leapfrog_steps,
                                                      momentum_distribution=momentum_distribution)

    num_adaptation_steps = int(0.8 * num_burnin_steps)
    kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)

    def trace_fn(state, pkr):
      return {
        'log_prob': target_log_prob(*state),
        'log_accept_ratio': pkr.inner_results.log_accept_ratio,
      }
    return tfm.sample_chain(
        num_results, initial_state,
        kernel=kernel,
        num_burnin_steps=num_burnin_steps,
        trace_fn=trace_fn,
        seed=sample_key)
  return run

Ci ancora una volta correre una volta per memorizzare nella cache il compilato run .

%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 56 s, sys: 1min 24s, total: 2min 20s
Wall time: 3min 35s

Ora lo eseguiremo di nuovo senza il sovraccarico della compilazione.

%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s
Wall time: 3min 1s

Sembra che abbiamo completato circa 150.000 passaggi di cavallina in circa 3 minuti, quindi circa 83 passaggi di cavallina al secondo! Tracciamo il rapporto di accettazione e la densità logaritmica dei nostri campioni.

fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
  ax.plot(val[0]) # Indexing into a sharded array, each element is the same
  ax.set_title(key);

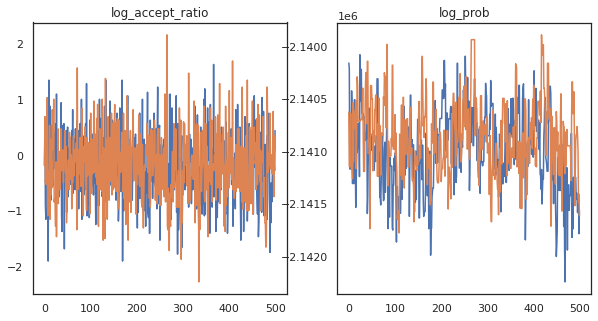
Ora che abbiamo alcuni campioni dalla nostra catena di Markov, usiamoli per fare alcune previsioni. Per prima cosa, estraiamo ciascuno dei componenti. Ricordate che le user_embeddings e user_bias sono spaccatura tra dispositivo, quindi abbiamo bisogno di concatenare il nostro ShardedArray per ottenerli tutti. D'altra parte, movie_embeddings e movie_bias sono uguali su ogni dispositivo, in modo da possiamo solo scegliere il valore dal primo frammento. Useremo regolare numpy per copiare i valori dalla parte posteriore TPU per CPU.

user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')

User embeddings: (500, 2, 6040, 20)
User bias: (500, 2, 6040)
Movie embeddings: (500, 2, 3706, 20)
Movie bias: (500, 2, 3706)

Proviamo a costruire un semplice sistema di raccomandazione che utilizzi l'incertezza catturata in questi campioni. Scriviamo prima una funzione che classifichi i film in base alla probabilità di visualizzazione.

@jax.jit
def recommend(sample, user_id):
  user_embeddings, user_bias, movie_embeddings, movie_bias = sample
  movie_logits = (
      jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
      + user_bias[user_id] + movie_bias)
  return movie_logits.argsort()[::-1]

Ora possiamo scrivere una funzione che esegua un ciclo su tutti i campioni e per ognuno selezioni il film in cima alla classifica che l'utente non ha già visto. Possiamo quindi vedere i conteggi di tutti i film consigliati nei campioni.

def get_recommendations(user_id): 
  movie_ids = []
  already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
  for i in range(500):
    for j in range(2):
      sample = jax.tree_map(lambda x: x[i, j], samples)
      ranking = recommend(sample, user_id)
      for movie_id in ranking:
        if int(movie_id) not in already_watched:
          movie_ids.append(movie_id)
          break
  return movie_ids

def plot_recommendations(movie_ids, ax=None):
  titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
  ax = ax or plt.gca()
  names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
  ax.bar(names, counts)
  ax.set_xticklabels(names, rotation=90)

Prendiamo l'utente che ha visto la maggior parte dei film rispetto a quello che ne ha visti di meno.

user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])

2314 20

Ci auguriamo che il nostro sistema ha più certezza su user_most di user_least , visto che abbiamo più informazioni su quali tipi di film user_most è più probabile che guardare.

fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');

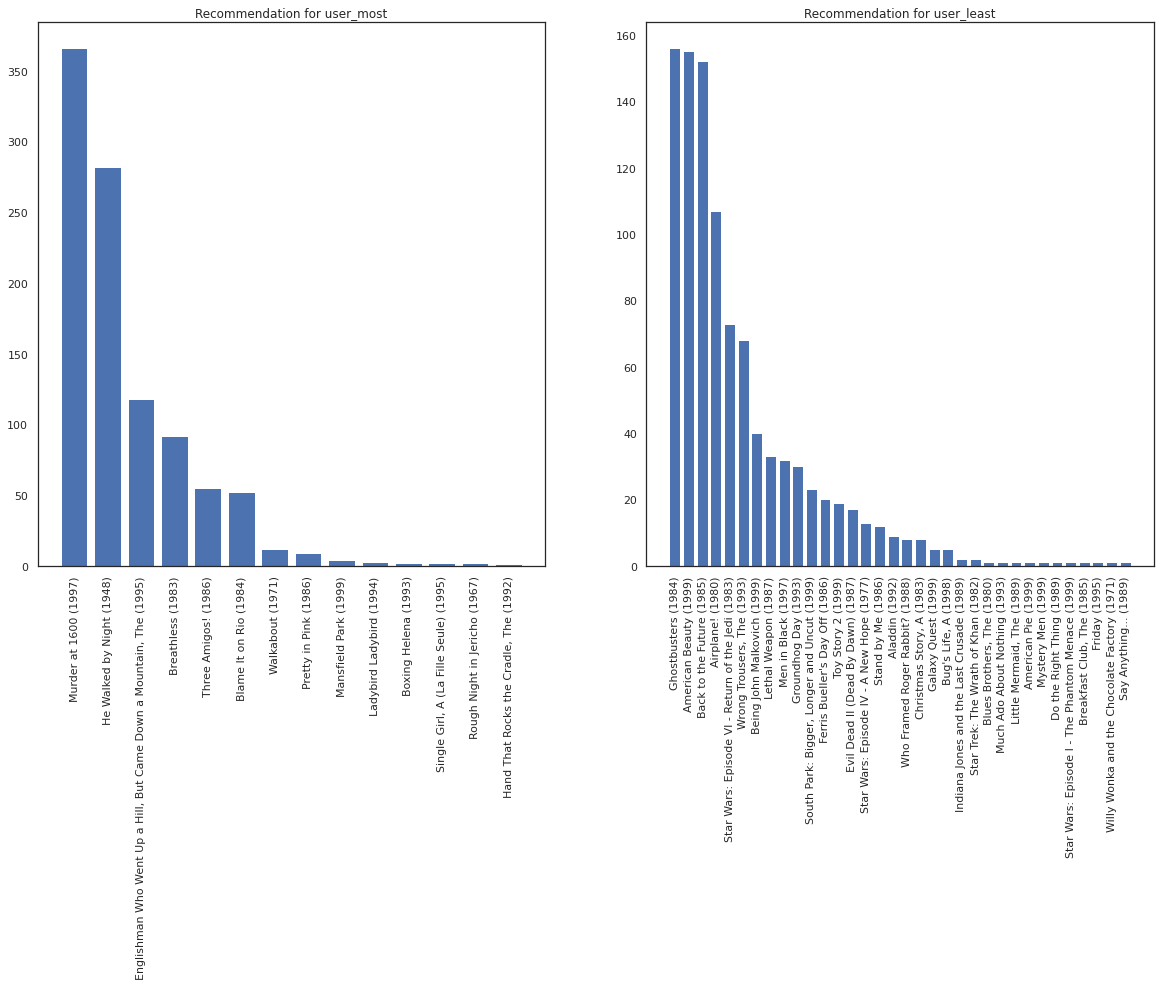
Vediamo che c'è più variabilità nelle nostre raccomandazioni per user_least che riflette la nostra ulteriore incertezza nelle loro preferenze di orologi.

Possiamo anche vedere guardare i generi dei film consigliati.

most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');

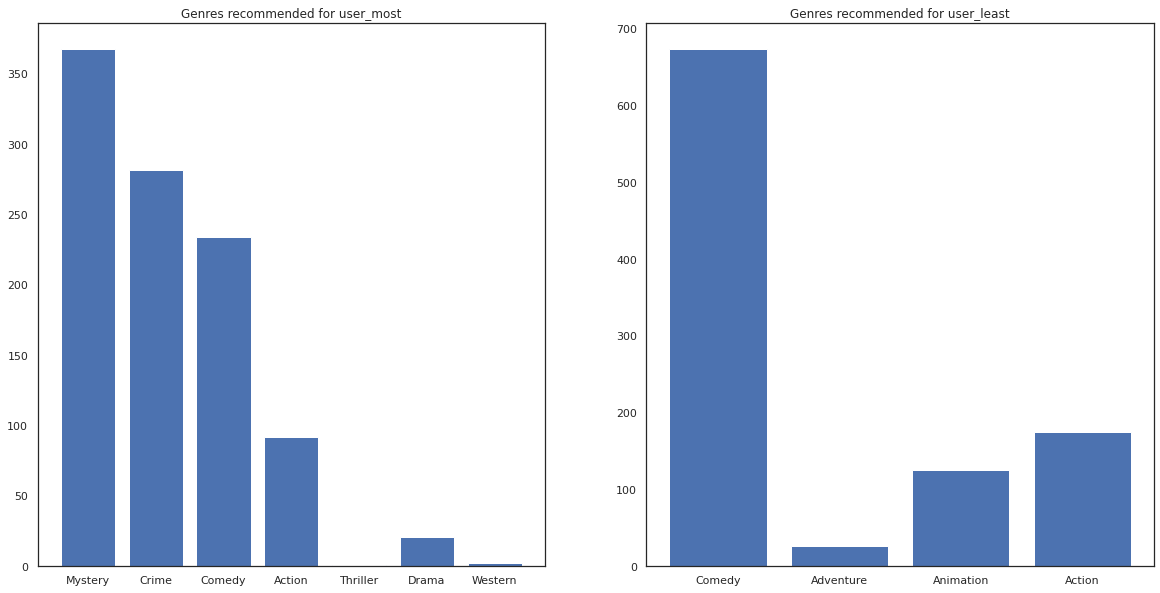
user_most ha visto un sacco di film ed è stato consigliato più generi di nicchia come il mistero e la criminalità, mentre user_least non ha guardato molti film ed è stato consigliato più film mainstream, che commedia skew e di azione.