Lihat di TensorFlow.org

Jalankan di Google Colab

Lihat sumber di GitHub

Unduh buku catatan

TensorFlow Probability (TFP) di JAX sekarang memiliki alat untuk komputasi numerik terdistribusi. Untuk menskalakan akselerator dalam jumlah besar, alat ini dibuat berdasarkan penulisan kode menggunakan paradigma "program tunggal multi-data", atau disingkat SPMD.

Di notebook ini, kita akan membahas cara "berpikir dalam SPMD" dan memperkenalkan abstraksi TFP baru untuk penskalaan ke konfigurasi seperti pod TPU, atau kluster GPU. Jika Anda menjalankan kode ini sendiri, pastikan untuk memilih runtime TPU.

Pertama-tama kita akan menginstal versi terbaru TFP, JAX dan TF.

Menginstal

pip install jaxlib --upgrade -q 2>&1 1> /dev/null
pip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/null
pip install tf-nightly-cpu -q -I 2>&1 1> /dev/null
pip install jax -I -q --upgrade 2>&1 1>/dev/null

Kami akan mengimpor beberapa perpustakaan umum, bersama dengan beberapa utilitas JAX.

Pengaturan dan Impor

import functools
import collections
import contextlib

import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds

from tensorflow_probability.substrates import jax as tfp

sns.set(style='white')

INFO:tensorflow:Enabling eager execution
INFO:tensorflow:Enabling v2 tensorshape
INFO:tensorflow:Enabling resource variables
INFO:tensorflow:Enabling tensor equality
INFO:tensorflow:Enabling control flow v2

Kami juga akan menyiapkan beberapa alias TFP yang praktis. Abstraksi baru saat ini disediakan dalam tfp.experimental.distribute dan tfp.experimental.mcmc .

tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc

Root = tfed.JointDistributionCoroutine.Root

Untuk menghubungkan notebook ke TPU, kami menggunakan helper berikut dari JAX. Untuk mengonfirmasi bahwa kami terhubung, kami mencetak jumlah perangkat, yang seharusnya delapan.

from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')

Found 8 devices

Sebuah pengantar cepat untuk jax.pmap

Setelah tersambung ke TPU, kita memiliki akses ke delapan perangkat. Namun, ketika kami menjalankan kode JAX dengan penuh semangat, JAX default untuk menjalankan komputasi hanya pada satu.

Cara paling sederhana untuk menjalankan komputasi di banyak perangkat adalah dengan memetakan suatu fungsi, dengan meminta setiap perangkat mengeksekusi satu indeks peta. JAX menyediakan jax.pmap ( "peta paralel") transformasi yang mengubah fungsi menjadi satu yang memetakan fungsi di beberapa perangkat.

Dalam contoh berikut, kami membuat larik berukuran 8 (agar sesuai dengan jumlah perangkat yang tersedia) dan memetakan fungsi yang menambahkan 5 di atasnya.

xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)

<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5.  6.  7.  8.  9. 10. 11. 12.]

Perhatikan bahwa kami menerima ShardedDeviceArray jenis kembali, menunjukkan bahwa output array secara fisik dibagi di perangkat.

jax.pmap bertindak semantis seperti peta, namun memiliki opsi penting yang memodifikasi perilaku. Secara default, pmap mengasumsikan semua masukan ke fungsi sedang dipetakan lebih, tapi kita bisa mengubah perilaku ini dengan in_axes argumen.

xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)

[ 5.  6.  7.  8.  9. 10. 11. 12.]

Analog, yang out_axes argumen untuk pmap menentukan apakah atau tidak untuk mengembalikan nilai-nilai pada setiap perangkat. Pengaturan out_axes ke None otomatis mengembalikan nilai pada perangkat 1 dan hanya boleh digunakan jika kami yakin nilai-nilai yang sama pada setiap perangkat.

xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)

2.0

Apa yang terjadi ketika apa yang ingin kita lakukan tidak mudah diekspresikan sebagai fungsi murni yang dipetakan? Misalnya, bagaimana jika kita ingin melakukan penjumlahan pada sumbu yang sedang kita petakan? JAX menawarkan "kolektif", fungsi yang berkomunikasi di seluruh perangkat, untuk memungkinkan penulisan program terdistribusi yang lebih menarik dan kompleks. Untuk memahami bagaimana tepatnya mereka bekerja, kami akan memperkenalkan SPMD.

Apa itu SPMD?

Single-program multiple-data (SPMD) adalah model pemrograman bersamaan di mana satu program (yaitu kode yang sama) dieksekusi secara bersamaan di seluruh perangkat, tetapi input ke setiap program yang berjalan dapat berbeda.

Jika program kami adalah fungsi sederhana dari input (yaitu sesuatu seperti x + 5 ), menjalankan program di SPMD hanya pemetaan itu data melalui berbeda, seperti yang kami lakukan dengan jax.pmap sebelumnya. Namun, kita dapat melakukan lebih dari sekadar "memetakan" suatu fungsi. JAX menawarkan "kolektif", yang merupakan fungsi yang berkomunikasi di seluruh perangkat.

Misalnya, mungkin kita ingin menjumlahkan kuantitas di semua perangkat kita. Sebelum kita melakukan itu, kita perlu menetapkan nama ke sumbu kita pemetaan berada lebih di pmap . Kami kemudian menggunakan lax.psum ( "sum paralel") berfungsi untuk melakukan penjumlahan seluruh perangkat, memastikan kami mengidentifikasi bernama sumbu kita menjumlahkan.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)

ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)

The psum agregat kolektif nilai x pada setiap perangkat dan mensinkronkan nilainya di peta yaitu out adalah 28. pada setiap perangkat. Kami tidak lagi melakukan "peta" sederhana, tetapi kami menjalankan program SPMD di mana komputasi setiap perangkat sekarang dapat berinteraksi dengan komputasi yang sama pada perangkat lain, meskipun dalam cara yang terbatas menggunakan kolektif. Dalam skenario ini, kita dapat menggunakan out_axes = None , karena psum akan melakukan sinkronisasi nilai.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))

ShardedDeviceArray(28., dtype=float32)

SPMD memungkinkan kita untuk menulis satu program yang dijalankan di setiap perangkat dalam konfigurasi TPU apa pun secara bersamaan. Kode yang sama yang digunakan untuk melakukan pembelajaran mesin pada 8 inti TPU dapat digunakan pada pod TPU yang mungkin memiliki ratusan hingga ribuan inti! Untuk tutorial yang lebih rinci tentang jax.pmap dan SPMD, Anda dapat merujuk ke para JAX 101 tutorial .

MCMC dalam skala besar

Dalam notebook ini, kami fokus menggunakan metode Markov Chain Monte Carlo (MCMC) untuk inferensi Bayesian. Ada beberapa cara kami menggunakan banyak perangkat untuk MCMC, tetapi di notebook ini, kami akan fokus pada dua:

1. Menjalankan rantai Markov independen pada perangkat yang berbeda. Kasus ini cukup sederhana dan dapat dilakukan dengan vanilla TFP.
2. Berbagi set data di seluruh perangkat. Kasus ini sedikit lebih rumit dan membutuhkan mesin TFP yang baru ditambahkan.

Rantai Independen

Katakanlah kami ingin melakukan inferensi Bayesian pada masalah menggunakan MCMC dan ingin menjalankan beberapa rantai secara paralel di beberapa perangkat (katakanlah 2 pada setiap perangkat). Ini ternyata merupakan program yang bisa kita "petakan" di seluruh perangkat, yaitu program yang tidak memerlukan kolektif. Untuk memastikan setiap program mengeksekusi rantai Markov yang berbeda (sebagai lawan menjalankan yang sama), kami memberikan nilai yang berbeda untuk seed acak ke setiap perangkat.

Mari kita coba pada masalah mainan pengambilan sampel dari distribusi Gaussian 2-D. Kita dapat menggunakan fungsionalitas MCMC TFP yang ada di luar kotak. Secara umum, kami mencoba menempatkan sebagian besar logika di dalam fungsi yang dipetakan untuk membedakan secara lebih eksplisit antara apa yang berjalan di semua perangkat versus hanya yang pertama.

def run(seed):
  target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob

  initial_state = jnp.zeros([2, 2]) # 2 chains
  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
  def trace_fn(state, pkr):
    return target_log_prob(state)

  states, log_prob = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    kernel=kernel,
    current_state=initial_state,
    trace_fn=trace_fn,
    seed=seed
  )
  return states, log_prob

Dengan sendirinya, run fungsi mengambil dalam benih acak stateless (untuk melihat bagaimana stateless keacakan kerja, Anda dapat membaca TFP pada JAX notebook atau melihat JAX 101 tutorial ). Pemetaan run lebih bibit yang berbeda akan menghasilkan menjalankan beberapa rantai Markov independen.

states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)

(8, 1000, 2, 2) (8, 1000, 2)

Perhatikan bagaimana kita sekarang memiliki sumbu tambahan yang sesuai dengan setiap perangkat. Kita dapat mengatur ulang dimensi dan meratakannya untuk mendapatkan sumbu untuk 16 rantai.

states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])

fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()

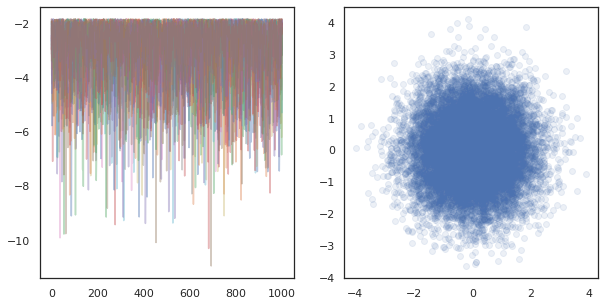
Saat menjalankan rantai independen pada banyak perangkat, itu semudah pmap -ing lebih fungsi yang menggunakan tfp.mcmc , memastikan kami melewati nilai yang berbeda untuk benih acak untuk masing-masing perangkat.

Membagi data

Ketika kami melakukan MCMC, distribusi target seringkali merupakan distribusi posterior yang diperoleh dengan mengkondisikan pada kumpulan data, dan menghitung kepadatan log yang tidak dinormalisasi melibatkan penjumlahan kemungkinan untuk setiap data yang diamati.

Dengan kumpulan data yang sangat besar, bahkan menjalankan satu rantai pada satu perangkat bisa sangat mahal. Namun, ketika kami memiliki akses ke beberapa perangkat, kami dapat membagi kumpulan data di seluruh perangkat untuk lebih memanfaatkan komputasi yang kami miliki.

Jika kita ingin melakukan MCMC dengan dataset sharded, kita perlu memastikan unnormalized log-density kita menghitung pada setiap perangkat mewakili total, yaitu kepadatan atas semua data, jika tidak setiap perangkat akan melakukan MCMC dengan sasaran yang salah mereka sendiri distribusi. Untuk tujuan ini, TFP sekarang memiliki alat baru (yaitu tfp.experimental.distribute dan tfp.experimental.mcmc ) yang memungkinkan komputasi "sharded" log probabilitas dan melakukan MCMC dengan mereka.

Distribusi yang dibagikan

Inti abstraksi TFP sekarang menyediakan untuk menghitung sharded probabiliities log adalah Sharded meta-distribusi, yang mengambil distribusi sebagai masukan dan mengembalikan distribusi baru yang memiliki sifat tertentu ketika dijalankan dalam konteks SPMD. Sharded kehidupan di tfp.experimental.distribute .

Secara intuitif, sebuah Sharded berkoresponden distribusi untuk satu set variabel acak yang telah "split" di seluruh perangkat. Pada setiap perangkat, mereka akan menghasilkan sampel yang berbeda, dan masing-masing dapat memiliki kepadatan log yang berbeda. Atau, sebuah Sharded berkoresponden distribusi ke "piring" di grafis Model bahasa, di mana piring ukuran adalah jumlah perangkat.

Sampling Sharded distribusi

Jika kita sampel dari Normal distribusi dalam program makhluk pmap -ed menggunakan benih yang sama pada setiap perangkat, kita akan mendapatkan sampel yang sama pada masing-masing perangkat. Kita dapat menganggap fungsi berikut sebagai pengambilan sampel variabel acak tunggal yang disinkronkan di seluruh perangkat.

# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
  return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                    -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32)

Jika kita membungkus tfd.Normal(0., 1.) dengan tfed.Sharded , kita secara logis sekarang memiliki delapan variabel acak yang berbeda (satu di setiap perangkat) dan karena itu akan menghasilkan sampel yang berbeda untuk masing-masing, meskipun lewat di benih yang sama .

def f(seed, _):
  return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([ 1.2152631 ,  0.7818249 ,  0.32549605,  0.6828047 ,
                     1.3973192 , -0.57830244,  0.37862757,  2.7706041 ],                   dtype=float32)

Representasi yang setara dari distribusi ini pada satu perangkat hanyalah 8 sampel normal independen. Meskipun nilai sampel akan berbeda ( tfed.Sharded tidak pseudo-acak nomor generasi sedikit berbeda), mereka berdua mewakili distribusi yang sama.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))

DeviceArray([ 0.08086783, -0.38624594, -0.3756545 ,  1.668957  ,
             -1.2758069 ,  2.1192007 , -0.85821325,  1.1305912 ],            dtype=float32)

Mengambil log-density dari Sharded distribusi

Mari kita lihat apa yang terjadi ketika kita menghitung kepadatan log sampel dari distribusi reguler dalam konteks SPMD.

def f(seed, _):
  dist = tfd.Normal(0., 1.)
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                     -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32),
 ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
                     -0.94012403, -0.94012403, -0.94012403, -0.94012403],                   dtype=float32))

Setiap sampel sama pada setiap perangkat, jadi kami menghitung kepadatan yang sama pada setiap perangkat juga. Secara intuitif, di sini kita hanya memiliki distribusi pada satu variabel terdistribusi normal.

Dengan Sharded distribusi, kami memiliki distribusi lebih dari 8 variabel acak, jadi ketika kita menghitung log_prob sampel, kita menjumlahkan, seluruh perangkat, lebih masing-masing dari kepadatan log individu. (Anda mungkin memperhatikan bahwa total nilai log_prob ini lebih besar dari log_prob tunggal yang dihitung di atas.)

def f(seed, _):
  dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
    random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)

Sample: [ 1.2152631   0.7818249   0.32549605  0.6828047   1.3973192  -0.57830244
  0.37862757  2.7706041 ]
Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205
 -13.7349205 -13.7349205]

Setara, distribusi "tidak di-sharding" menghasilkan kepadatan log yang sama.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)

DeviceArray(-13.7349205, dtype=float32)

Sebuah Sharded distribusi menghasilkan nilai yang berbeda dari sample pada masing-masing perangkat, tetapi mendapatkan nilai yang sama untuk log_prob pada setiap perangkat. Apa yang sedang terjadi disini? Sebuah Sharded distribusi melakukan psum internal untuk memastikan log_prob nilai-nilai yang di sync di perangkat. Mengapa kita menginginkan perilaku ini? Jika kita menjalankan rantai MCMC yang sama pada masing-masing perangkat, kami ingin yang target_log_prob menjadi sama di masing-masing perangkat, bahkan jika beberapa variabel acak dalam perhitungan yang sharded di seluruh perangkat.

Selain itu, Sharded Memastikan distribusi yang gradien seluruh perangkat adalah benar, untuk memastikan bahwa algoritma seperti HMC, yang mengambil gradien dari fungsi log-density sebagai bagian dari fungsi transisi, menghasilkan sampel yang tepat.

Sharded JointDistribution s

Kita bisa membuat model dengan beberapa Sharded variabel acak dengan menggunakan JointDistribution s (JDs). Sayangnya, Sharded distribusi tidak dapat dengan aman digunakan harus dengan vanili tfd.JointDistribution s, tapi tfp.experimental.distribute ekspor "ditambal" JDs yang akan berperilaku seperti Sharded distribusi.

def f(seed, _):
  dist = tfed.JointDistributionSequential([
    tfd.Normal(0., 1.),
    tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
  ])
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
                      1.6121525, 1.6121525, 1.6121525], dtype=float32),
  ShardedDeviceArray([ 0.8690128 , -0.83167845,  1.2209264 ,  0.88412696,
                       0.76478404, -0.66208494, -0.0129658 ,  0.7391483 ],                   dtype=float32)],
 ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
                     -12.214451, -12.214451, -12.214451, -12.214451],                   dtype=float32))

Ini JDs sharded dapat memiliki keduanya Sharded dan vanili TFP distribusi sebagai komponen. Untuk distribusi unsharded, kami mendapatkan sampel yang sama pada setiap perangkat, dan untuk distribusi sharded, kami mendapatkan sampel yang berbeda. The log_prob pada setiap perangkat disinkronisasi juga.

MCMC dengan Sharded distribusi

Bagaimana kita berpikir tentang Sharded distribusi dalam konteks MCMC? Jika kita memiliki model generatif yang dapat dinyatakan sebagai JointDistribution , kita dapat memilih beberapa sumbu model yang ke "pecahan" di. Biasanya, satu variabel acak dalam model akan sesuai dengan data yang diamati, dan jika kami memiliki kumpulan data besar yang ingin kami sharding di seluruh perangkat, kami ingin variabel yang terkait dengan titik data juga di-sharding. Kami juga mungkin memiliki variabel acak "lokal" yang satu-ke-satu dengan pengamatan yang kami sharding, jadi kami harus menambahkan variabel acak tersebut.

Kami akan pergi ke contoh penggunaan Sharded distribusi dengan TFP MCMC di bagian ini. Kita akan mulai dengan contoh regresi logistik Bayesian sederhana, dan menyimpulkan dengan contoh matriks faktorisasi, dengan tujuan menunjukkan beberapa penggunaan-kasus untuk distribute perpustakaan.

Contoh: Regresi logistik Bayesian untuk MNIST

Kami ingin melakukan regresi logistik Bayesian pada kumpulan data yang besar; Model ini memiliki sebelum \(p(\theta)\) atas bobot regresi, dan kemungkinan \(p(y_i | \theta, x_i)\) yang dijumlahkan atas semua data \(\{x_i, y_i\}_{i = 1}^N\) untuk mendapatkan total kepadatan log bersama. Jika kita beling data kami, kami akan beling variabel-variabel acak diamati \(x_i\) dan \(y_i\) dalam model kami.

Kami menggunakan model regresi logistik Bayesian berikut untuk klasifikasi MNIST:

\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]

Mari muat MNIST menggunakan Kumpulan Data TensorFlow.

mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.

raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.

Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1...
WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your
local data directory. If you'd instead prefer to read directly from our public
GCS bucket (recommended if you're running on GCP), you can instead pass
`try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`.
HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio…
Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.

Kami memiliki 60000 gambar pelatihan tetapi mari kita manfaatkan 8 inti yang tersedia dan membaginya menjadi 8 cara. Kami akan menggunakan ini berguna shard fungsi utilitas.

def shard_value(x):
  x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
  return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices

shard = functools.partial(jax.tree_map, shard_value)

sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)

(8, 7500, 784) (8, 7500)

Sebelum melanjutkan, mari kita bahas presisi pada TPU dan dampaknya pada HMC. TPUs mengeksekusi perkalian matriks menggunakan rendah bfloat16 presisi untuk kecepatan. bfloat16 matriks perkalian sering cukup untuk banyak aplikasi pembelajaran dalam, tapi bila digunakan dengan HMC, kami telah secara empiris menemukan presisi yang lebih rendah dapat menyebabkan divergen lintasan, menyebabkan penolakan. Kita dapat menggunakan perkalian matriks presisi yang lebih tinggi, dengan biaya beberapa komputasi tambahan.

Untuk meningkatkan presisi matmul kami, kita dapat menggunakan jax.default_matmul_precision dekorator dengan "tensorfloat32" presisi (untuk presisi yang lebih tinggi kita bisa menggunakan "float32" presisi).

Sekarang mari kita mendefinisikan kita run fungsi, yang akan mengambil benih acak (yang akan sama pada setiap perangkat) dan pecahan MNIST. Fungsi tersebut akan mengimplementasikan model yang disebutkan di atas dan kami kemudian akan menggunakan fungsionalitas vanilla MCMC TFP untuk menjalankan satu rantai. Kami akan pastikan untuk menghias run dengan jax.default_matmul_precision dekorator untuk memastikan perkalian matriks dijalankan dengan presisi tinggi, meskipun dalam contoh khusus di bawah ini, kami hanya juga bisa menggunakan jnp.dot(images, w, precision=lax.Precision.HIGH) .

# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device. 
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
  images, labels = data # a sharded dataset
  num_examples, dim = images.shape
  num_classes = 10

  def model_fn():
    w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
    b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
    logits = jnp.dot(images, w) + b
    yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
                       shard_axis_name='data')
  model = tfed.JointDistributionCoroutine(model_fn)

  init_seed, sample_seed = random.split(seed)

  initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`

  def target_log_prob(*state):
    return model.log_prob((*state, labels))

  def accuracy(w, b):
    logits = images.dot(w) + b
    preds = logits.argmax(axis=-1)
    # We take the average accuracy across devices by using `lax.pmean`
    return lax.pmean((preds == labels).mean(), 'data')

  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
  kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
  def trace_fn(state, pkr):
    return (
        target_log_prob(*state),
        accuracy(*state),
        pkr.new_step_size)
  states, trace = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    current_state=initial_state,
    kernel=kernel,
    trace_fn=trace_fn,
    seed=sample_seed
  )
  return states, trace

jax.pmap termasuk kompilasi JIT tapi fungsi dikompilasi cache setelah panggilan pertama. Kami akan memanggil run dan mengabaikan output untuk cache kompilasi.

%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s
Wall time: 1min 54s

Kami akan sekarang panggilan run lagi untuk melihat berapa lama eksekusi yang sebenarnya terjadi.

%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s
Wall time: 1min 43s

Kami menjalankan 200.000 langkah lompatan, yang masing-masing menghitung gradien di seluruh kumpulan data. Memisahkan komputasi lebih dari 8 core memungkinkan kita untuk menghitung setara dengan 200.000 epoch pelatihan dalam waktu sekitar 95 detik, sekitar 2.100 epoch per detik!

Mari kita plot densitas log dari setiap sampel dan akurasi setiap sampel:

fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()

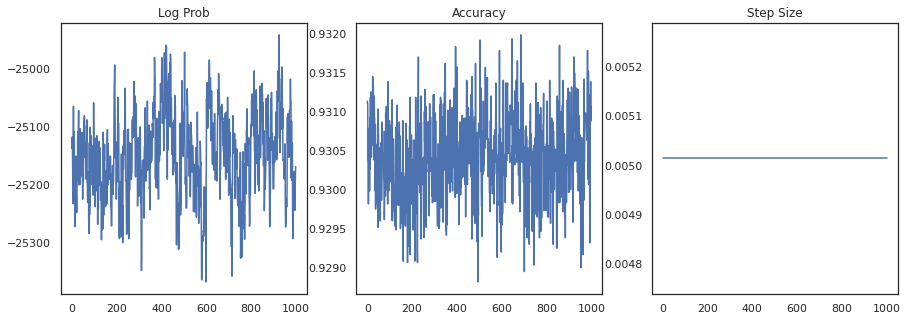
Jika kita menggabungkan sampel, kita dapat menghitung rata-rata model Bayesian untuk meningkatkan kinerja kita.

@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
  images, labels = data
  logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
  probs = jax.nn.softmax(logits, axis=-1)
  bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
  avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
  return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')

sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')

Average Accuracy: 0.9188529253005981
BMA Accuracy: 0.9264000058174133
Accuracy Improvement: 0.0075470805168151855

Rata-rata model Bayesian meningkatkan akurasi kami hampir 1%!

Contoh: Sistem rekomendasi MovieLens

Sekarang mari kita coba melakukan inferensi dengan kumpulan data rekomendasi MovieLens, yang merupakan kumpulan pengguna dan peringkat mereka dari berbagai film. Secara khusus, kita dapat mewakili MovieLens sebagai \(N \times M\) menonton matriks \(W\) mana \(N\) adalah jumlah pengguna dan \(M\) adalah jumlah film; kami berharap \(N > M\). Entri dari \(W_{ij}\) adalah boolean yang menunjukkan apakah atau tidak pengguna \(i\) menonton film \(j\). Perhatikan bahwa MovieLens memberikan peringkat pengguna, tetapi kami mengabaikannya untuk menyederhanakan masalah.

Pertama, kita akan memuat dataset. Kami akan menggunakan versi dengan 1 juta peringkat.

movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
          'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
          'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
          'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']

Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0...
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl…

HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value='')))
Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord
HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value='')))
Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.

Kami akan melakukan beberapa preprocessing dari dataset untuk mendapatkan jam tangan matriks \(W\).

raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']

movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])

num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1

movie_titles = dict(zip(movielens['train']['movie_id'],
                        movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
                        genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
                     for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]

watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)

(6040, 3706)

Kita bisa menentukan model generatif untuk \(W\), menggunakan matriks probabilistik model yang faktorisasi sederhana. Kami mengasumsikan laten \(N \times D\) matrix pengguna \(U\) dan laten \(M \times D\) matriks film \(V\), yang bila dikalikan menghasilkan logits dari Bernoulli untuk menonton matriks \(W\). Kami juga akan menyertakan vektor bias untuk pengguna dan film, \(u\) dan \(v\).

\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]

Ini adalah matriks yang cukup besar; 6040 pengguna dan 3706 film mengarah ke matriks dengan lebih dari 22 juta entri di dalamnya. Bagaimana kita mendekati sharding model ini? Nah, jika kita menganggap bahwa \(N > M\) (yaitu ada lebih banyak pengguna dari film), maka akan masuk akal untuk beling menonton matriks di sumbu pengguna, sehingga masing-masing perangkat akan memiliki sepotong menonton matriks sesuai dengan subset dari pengguna . Berbeda dengan contoh sebelumnya, namun, kami akan juga harus beling sampai \(U\) matriks, karena memiliki embedding untuk setiap pengguna, sehingga masing-masing perangkat akan bertanggung jawab untuk pecahan \(U\) dan pecahan \(W\). Di sisi lain, \(V\) akan unsharded dan disinkronkan di seluruh perangkat.

sharded_watch_matrix = shard(watch_matrix)

Sebelum kita menulis kita run , mari kita cepat mendiskusikan tantangan tambahan sharding lokal variabel acak \(U\). Saat menjalankan HMC, vanili tfp.mcmc.HamiltonianMonteCarlo kernel akan sampel momentum untuk setiap elemen negara rantai. Sebelumnya, hanya variabel acak yang tidak di-sharding yang merupakan bagian dari status itu, dan momentumnya sama di setiap perangkat. Ketika kita sekarang memiliki sharded \(U\), kita perlu sampel momentum yang berbeda pada setiap perangkat untuk \(U\), sementara sampel momentum yang sama untuk \(V\). Untuk mencapai hal ini, kita dapat menggunakan tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo dengan Sharded distribusi momentum. Saat kami terus membuat komputasi paralel kelas satu, kami dapat menyederhanakan ini, misalnya dengan mengambil indikator shardedness ke kernel HMC.

def make_run(*,
             axis_name,
             dim=20,
             num_chains=2,
             prior_variance=1.,
             step_size=1e-2,
             num_leapfrog_steps=100,
             num_burnin_steps=1000,
             num_results=500,
             ):
  @functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
  @jax.default_matmul_precision('tensorfloat32')
  def run(key, watch_matrix):
    num_users, num_movies = watch_matrix.shape

    Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)

    def prior_fn():
      user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
      user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
      movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
      movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
      return (user_embeddings, user_bias, movie_embeddings, movie_bias)
    prior = tfed.JointDistributionCoroutine(prior_fn)

    def model_fn():
      user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
      logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
                + user_bias[..., :, None] + movie_bias[..., None, :])
      yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
    model = tfed.JointDistributionCoroutine(model_fn)

    init_key, sample_key = random.split(key)
    initial_state = prior.sample(seed=init_key, sample_shape=num_chains)

    def target_log_prob(*state):
      return model.log_prob((*state, watch_matrix))

    momentum_distribution = tfed.JointDistributionSequential([
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
    ])

    # We pass in momentum_distribution here to ensure that the momenta for 
    # user_embeddings and user_bias are also sharded
    kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
                                                      num_leapfrog_steps,
                                                      momentum_distribution=momentum_distribution)

    num_adaptation_steps = int(0.8 * num_burnin_steps)
    kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)

    def trace_fn(state, pkr):
      return {
        'log_prob': target_log_prob(*state),
        'log_accept_ratio': pkr.inner_results.log_accept_ratio,
      }
    return tfm.sample_chain(
        num_results, initial_state,
        kernel=kernel,
        num_burnin_steps=num_burnin_steps,
        trace_fn=trace_fn,
        seed=sample_key)
  return run

Kami akan lagi menjalankannya sekali untuk cache disusun run .

%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 56 s, sys: 1min 24s, total: 2min 20s
Wall time: 3min 35s

Sekarang kita akan menjalankannya lagi tanpa overhead kompilasi.

%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s
Wall time: 3min 1s

Sepertinya kita menyelesaikan sekitar 150.000 langkah lompatan katak dalam waktu sekitar 3 menit, jadi sekitar 83 langkah lompatan katak per detik! Mari kita plot rasio penerimaan dan kepadatan log dari sampel kita.

fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
  ax.plot(val[0]) # Indexing into a sharded array, each element is the same
  ax.set_title(key);

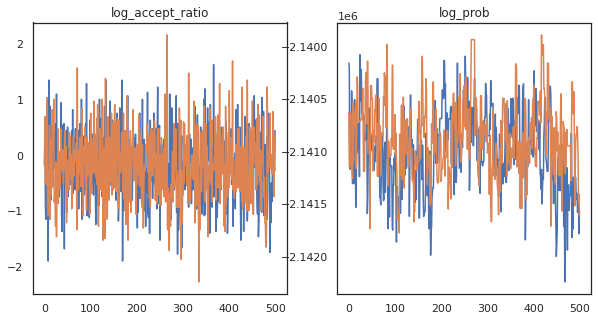
Sekarang kita memiliki beberapa sampel dari rantai Markov, mari kita gunakan untuk membuat beberapa prediksi. Pertama, mari kita ekstrak masing-masing komponen. Ingat bahwa user_embeddings dan user_bias adalah split di perangkat, jadi kita perlu menggabungkan kami ShardedArray untuk mendapatkan mereka semua. Di sisi lain, movie_embeddings dan movie_bias adalah sama pada setiap perangkat, jadi kami hanya bisa memilih nilai dari beling pertama. Kami akan menggunakan reguler numpy untuk menyalin nilai dari TPUs kembali ke CPU.

user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')

User embeddings: (500, 2, 6040, 20)
User bias: (500, 2, 6040)
Movie embeddings: (500, 2, 3706, 20)
Movie bias: (500, 2, 3706)

Mari kita coba membangun sistem rekomendasi sederhana yang memanfaatkan ketidakpastian yang ditangkap dalam sampel ini. Pertama-tama mari kita tulis fungsi yang memberi peringkat film menurut probabilitas tontonan.

@jax.jit
def recommend(sample, user_id):
  user_embeddings, user_bias, movie_embeddings, movie_bias = sample
  movie_logits = (
      jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
      + user_bias[user_id] + movie_bias)
  return movie_logits.argsort()[::-1]

Kita sekarang dapat menulis fungsi yang mengulang semua sampel dan untuk masing-masing sampel, memilih film peringkat teratas yang belum pernah ditonton pengguna. Kami kemudian dapat melihat jumlah semua film yang direkomendasikan di seluruh sampel.

def get_recommendations(user_id): 
  movie_ids = []
  already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
  for i in range(500):
    for j in range(2):
      sample = jax.tree_map(lambda x: x[i, j], samples)
      ranking = recommend(sample, user_id)
      for movie_id in ranking:
        if int(movie_id) not in already_watched:
          movie_ids.append(movie_id)
          break
  return movie_ids

def plot_recommendations(movie_ids, ax=None):
  titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
  ax = ax or plt.gca()
  names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
  ax.bar(names, counts)
  ax.set_xticklabels(names, rotation=90)

Mari kita ambil pengguna yang paling banyak menonton film versus yang paling sedikit menonton.

user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])

2314 20

Kami berharap sistem kami memiliki lebih kepastian tentang user_most dari user_least , mengingat bahwa kita memiliki informasi lebih lanjut tentang apa macam film user_most lebih mungkin untuk menonton.

fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');

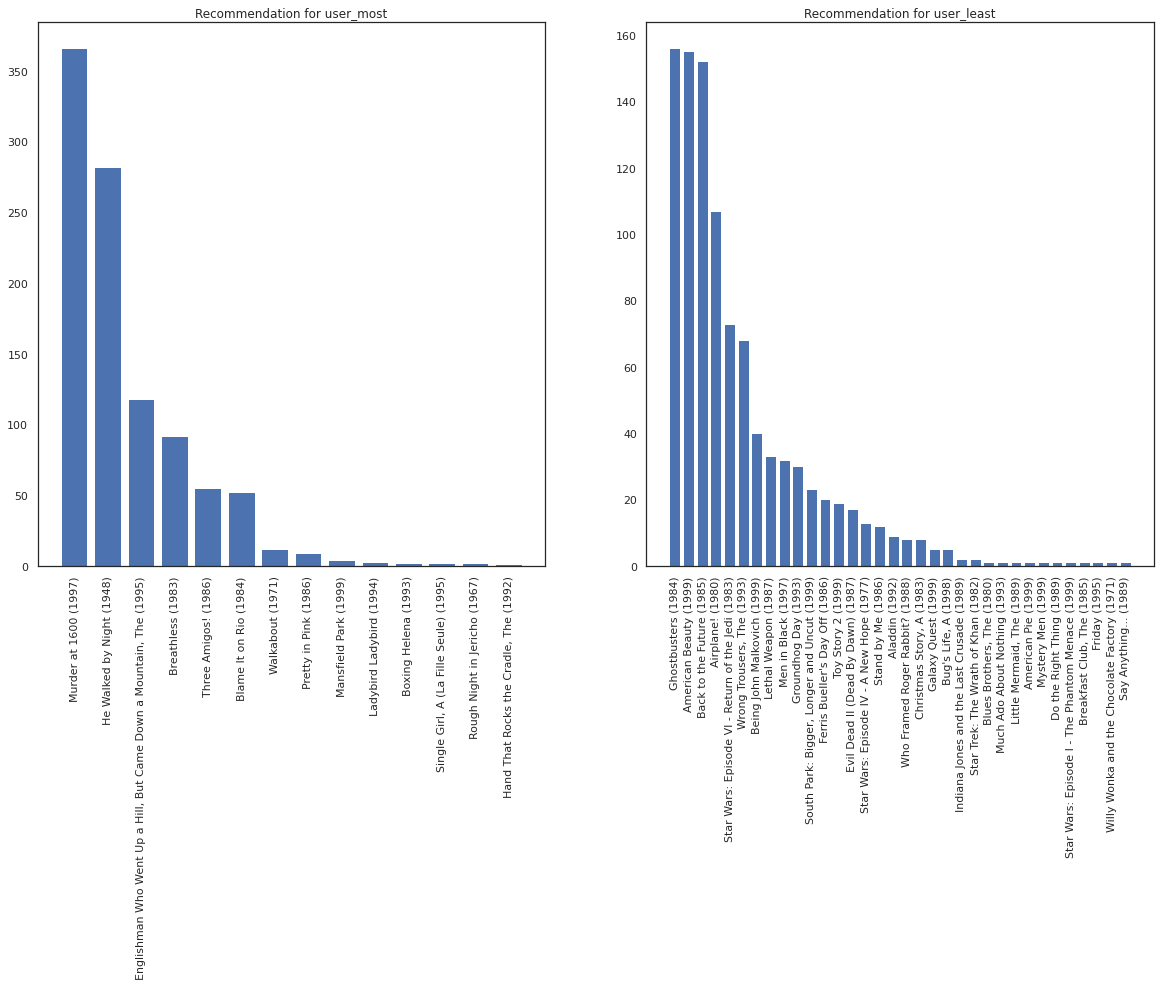
Kita melihat bahwa ada lebih varians dalam rekomendasi kami untuk user_least mencerminkan ketidakpastian tambahan kami dalam preferensi menonton mereka.

Kita juga bisa melihat genre film yang direkomendasikan.

most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');

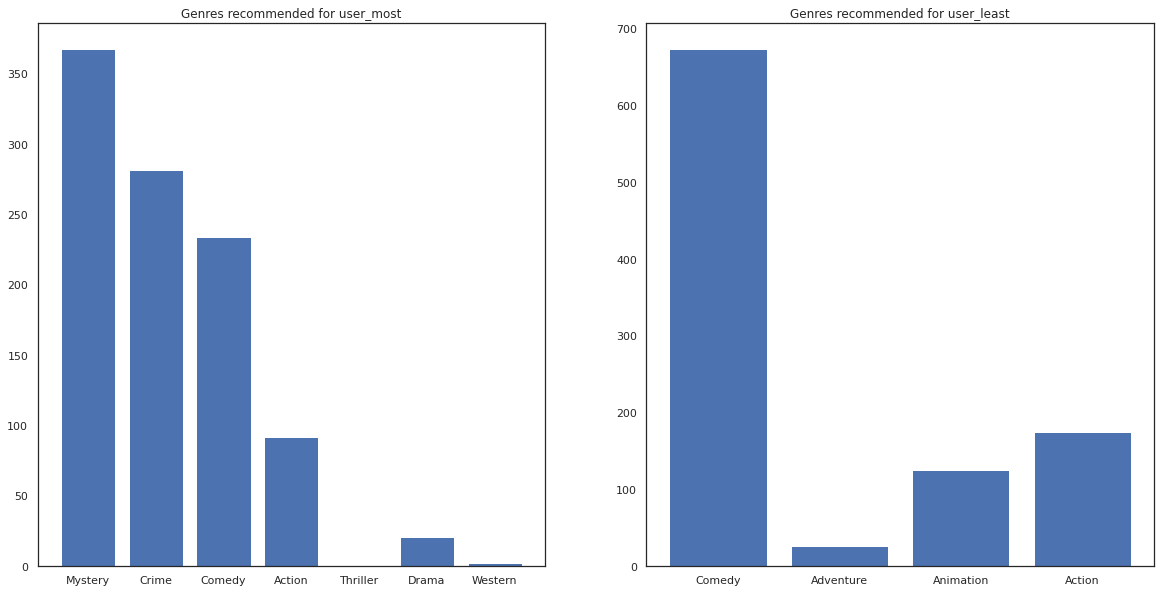
user_most telah melihat banyak film dan telah direkomendasikan lebih genre niche seperti misteri dan kejahatan sedangkan user_least belum menonton banyak film dan direkomendasikan film lebih utama, yang komedi miring dan tindakan.