TensorFlow.org पर देखें

Google Colab में चलाएं

GitHub पर स्रोत देखें

नोटबुक डाउनलोड करें

JAX पर TensorFlow Probability (TFP) में अब वितरित संख्यात्मक कंप्यूटिंग के लिए उपकरण हैं। बड़ी संख्या में त्वरक के पैमाने के लिए, उपकरण "सिंगल-प्रोग्राम मल्टीपल-डेटा" प्रतिमान, या संक्षेप में SPMD का उपयोग करके कोड लिखने के लिए बनाए गए हैं।

इस नोटबुक में, हम "एसपीएमडी में सोचने" के बारे में जानेंगे और टीपीयू पॉड्स, या जीपीयू के क्लस्टर जैसे कॉन्फ़िगरेशन में स्केलिंग के लिए नए टीएफपी एब्स्ट्रैक्शन पेश करेंगे। यदि आप इस कोड को स्वयं चला रहे हैं, तो सुनिश्चित करें कि आप TPU रनटाइम का चयन करें।

हम सबसे पहले नवीनतम संस्करण TFP, JAX और TF स्थापित करेंगे।

इंस्टॉल

pip install jaxlib --upgrade -q 2>&1 1> /dev/null
pip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/null
pip install tf-nightly-cpu -q -I 2>&1 1> /dev/null
pip install jax -I -q --upgrade 2>&1 1>/dev/null

हम कुछ JAX उपयोगिताओं के साथ कुछ सामान्य पुस्तकालय आयात करेंगे।

सेटअप और आयात

import functools
import collections
import contextlib

import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds

from tensorflow_probability.substrates import jax as tfp

sns.set(style='white')

INFO:tensorflow:Enabling eager execution
INFO:tensorflow:Enabling v2 tensorshape
INFO:tensorflow:Enabling resource variables
INFO:tensorflow:Enabling tensor equality
INFO:tensorflow:Enabling control flow v2

हम कुछ उपयोगी TFP उपनाम भी स्थापित करेंगे। नई कपोल-कल्पना वर्तमान में प्रदान की जाती हैं tfp.experimental.distribute और tfp.experimental.mcmc ।

tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc

Root = tfed.JointDistributionCoroutine.Root

नोटबुक को टीपीयू से जोड़ने के लिए, हम जेएक्स से निम्नलिखित सहायक का उपयोग करते हैं। यह पुष्टि करने के लिए कि हम जुड़े हुए हैं, हम उपकरणों की संख्या का प्रिंट आउट लेते हैं, जो आठ होनी चाहिए।

from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')

Found 8 devices

के लिए एक त्वरित परिचय jax.pmap

एक TPU से कनेक्ट होने के बाद, हम आठ डिवाइस की पहुंच है। हालांकि, जब हम जेएक्स कोड को उत्सुकता से चलाते हैं, तो जेएक्स केवल एक पर गणना चलाने के लिए डिफ़ॉल्ट होता है।

कई उपकरणों में गणना को निष्पादित करने का सबसे सरल तरीका एक फ़ंक्शन को मैप करना है, जिसमें प्रत्येक डिवाइस मैप के एक इंडेक्स को निष्पादित करता है। JAX प्रदान करता है jax.pmap ( "समानांतर नक्शा") परिवर्तन जो एक कई उपकरणों भर में समारोह के नक्शे कि में एक समारोह बदल जाता है।

निम्नलिखित उदाहरण में, हम आकार 8 (उपलब्ध उपकरणों की संख्या से मेल खाने के लिए) की एक सरणी बनाते हैं और एक फ़ंक्शन को मैप करते हैं जो इसमें 5 जोड़ता है।

xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)

<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5.  6.  7.  8.  9. 10. 11. 12.]

नोट हम एक प्राप्त होने वाले ShardedDeviceArray प्रकार वापस, यह दर्शाता है कि उत्पादन सरणी शारीरिक रूप से सभी डिवाइस में विभाजित है।

jax.pmap शब्दार्थ मानचित्र की तरह काम करता है, लेकिन कुछ महत्वपूर्ण विकल्प अपने व्यवहार को संशोधित करता है। डिफ़ॉल्ट रूप से, pmap मान लिया गया कार्य करने के लिए सभी आदानों से अधिक मैप किया जा रहा है, लेकिन हम के साथ इस व्यवहार को संशोधित कर सकते हैं in_axes तर्क।

xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)

[ 5.  6.  7.  8.  9. 10. 11. 12.]

तुलनात्मक रूप से, out_axes को तर्क pmap निर्धारित करता है या नहीं, हर डिवाइस पर मान वापस जाने के लिए। स्थापना out_axes को None स्वचालित रूप से 1 डिवाइस पर मान देता है और केवल तभी जब हमें विश्वास है मानों हर डिवाइस पर ही कर रहे हैं कर रहे हैं प्रयोग किया जाना चाहिए।

xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)

2.0

क्या होता है जब हम जो करना चाहते हैं उसे मैप किए गए शुद्ध फ़ंक्शन के रूप में आसानी से व्यक्त नहीं किया जा सकता है? उदाहरण के लिए, क्या होगा यदि हम उस अक्ष पर एक योग करना चाहते हैं जिस पर हम मानचित्रण कर रहे हैं? JAX अधिक दिलचस्प और जटिल वितरित प्रोग्राम लिखने में सक्षम बनाने के लिए "सामूहिक" फ़ंक्शन प्रदान करता है जो उपकरणों में संचार करता है। यह समझने के लिए कि वे वास्तव में कैसे काम करते हैं, हम SPMD का परिचय देंगे।

एसपीएमडी क्या है?

सिंगल-प्रोग्राम मल्टीपल-डेटा (SPMD) एक समवर्ती प्रोग्रामिंग मॉडल है जिसमें एक ही प्रोग्राम (यानी एक ही कोड) को एक साथ सभी उपकरणों में निष्पादित किया जाता है, लेकिन प्रत्येक चल रहे प्रोग्राम के इनपुट भिन्न हो सकते हैं।

यदि हमारे कार्यक्रम अपने आदानों की एक साधारण समारोह (जैसे यानी कुछ है x + 5 ), SPMD में एक कार्यक्रम चल रहा है बस इसे से अधिक विभिन्न डेटा मैपिंग कर रहा है, जैसे हम साथ किया था jax.pmap पहले। हालाँकि, हम एक फ़ंक्शन को केवल "मैप" करने के अलावा और भी बहुत कुछ कर सकते हैं। JAX "सामूहिक" प्रदान करता है, जो ऐसे कार्य हैं जो सभी उपकरणों में संचार करते हैं।

उदाहरण के लिए, हो सकता है कि हम अपने सभी उपकरणों में मात्रा का योग लेना चाहें। इससे पहले कि हम ऐसा करते हैं, हम एक नाम प्रदान करते हैं हम में से अधिक है मानचित्रण अक्ष की जरूरत pmap । इसके बाद हम lax.psum वाले डिवाइस पर एक योग प्रदर्शन करने के लिए ( "समानांतर योग") समारोह, हम की पहचान नामित अक्ष हम अधिक संक्षेप रहे हैं सुनिश्चित करता है।

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)

ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)

psum सामूहिक समुच्चय के मूल्य x प्रत्येक डिवाइस पर और सिंक्रनाइज़ करता नक्शा भर में अपने मूल्य यानी out है 28. प्रत्येक डिवाइस पर। हम अब एक साधारण "मानचित्र" का प्रदर्शन नहीं कर रहे हैं, लेकिन हम एक एसपीएमडी प्रोग्राम निष्पादित कर रहे हैं जहां प्रत्येक डिवाइस की गणना अब अन्य उपकरणों पर समान गणना के साथ बातचीत कर सकती है, भले ही सामूहिक रूप से सीमित तरीके से। इस परिदृश्य में, हम उपयोग कर सकते हैं out_axes = None , क्योंकि psum मूल्य सिंक्रनाइज़ किए जाएंगे।

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))

ShardedDeviceArray(28., dtype=float32)

SPMD हमें एक प्रोग्राम लिखने में सक्षम बनाता है जो किसी भी TPU कॉन्फ़िगरेशन में प्रत्येक डिवाइस पर एक साथ चलाया जाता है। 8 टीपीयू कोर पर मशीन लर्निंग करने के लिए इस्तेमाल किया जाने वाला एक ही कोड टीपीयू पॉड पर इस्तेमाल किया जा सकता है जिसमें सैकड़ों से हजारों कोर हो सकते हैं! के बारे में विस्तृत ट्यूटोरियल के लिए jax.pmap और SPMD, आप का उल्लेख कर सकते JAX 101 ट्यूटोरियल ।

पैमाने पर एमसीएमसी

इस नोटबुक में, हम बायेसियन अनुमान के लिए मार्कोव चेन मोंटे कार्लो (एमसीएमसी) विधियों का उपयोग करने पर ध्यान केंद्रित करते हैं। एमसीएमसी के लिए हम कई तरह के उपकरणों का उपयोग कर सकते हैं, लेकिन इस नोटबुक में, हम दो पर ध्यान देंगे:

1. विभिन्न उपकरणों पर स्वतंत्र मार्कोव श्रृंखला चलाना। यह मामला काफी सरल है और वेनिला टीएफपी के साथ करना संभव है।
2. सभी उपकरणों में डेटासेट साझा करना। यह मामला थोड़ा अधिक जटिल है और इसके लिए हाल ही में जोड़ी गई TFP मशीनरी की आवश्यकता है।

स्वतंत्र जंजीर

मान लें कि हम एमसीएमसी का उपयोग करके किसी समस्या पर बायेसियन अनुमान करना चाहते हैं और कई उपकरणों में समानांतर में कई श्रृंखलाएं चलाना चाहते हैं (प्रत्येक डिवाइस पर 2 कहें)। यह एक ऐसा प्रोग्राम बन जाता है जिसे हम सभी डिवाइसों में केवल "मानचित्र" कर सकते हैं, अर्थात ऐसा जिसे किसी समूह की आवश्यकता नहीं है। यह सुनिश्चित करने के लिए कि प्रत्येक प्रोग्राम एक अलग मार्कोव श्रृंखला निष्पादित करता है (उसी को चलाने के विपरीत), हम प्रत्येक डिवाइस के लिए यादृच्छिक बीज के लिए एक अलग मान में पास करते हैं।

आइए इसे 2-डी गाऊसी वितरण से नमूने की एक खिलौना समस्या पर आज़माएं। हम टीएफपी की मौजूदा एमसीएमसी कार्यक्षमता का बिल्कुल अलग उपयोग कर सकते हैं। सामान्य तौर पर, हम अपने मैप किए गए फ़ंक्शन के अंदर अधिकांश तर्क डालने का प्रयास करते हैं ताकि सभी उपकरणों पर चल रहे पहले बनाम पहले के बीच स्पष्ट रूप से अंतर किया जा सके।

def run(seed):
  target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob

  initial_state = jnp.zeros([2, 2]) # 2 chains
  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
  def trace_fn(state, pkr):
    return target_log_prob(state)

  states, log_prob = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    kernel=kernel,
    current_state=initial_state,
    trace_fn=trace_fn,
    seed=seed
  )
  return states, log_prob

अपने आप से, run समारोह एक राज्यविहीन यादृच्छिक बीज में ले जाता है (देखने के लिए कैसे राज्यविहीन अनियमितता काम करते हैं, आप पढ़ सकते हैं JAX पर TFP नोटबुक या देखना JAX 101 ट्यूटोरियल )। मानचित्रण run विभिन्न बीज पर कई स्वतंत्र मार्कोव चेन चलाने में परिणाम देगा।

states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)

(8, 1000, 2, 2) (8, 1000, 2)

ध्यान दें कि अब हमारे पास प्रत्येक डिवाइस के अनुरूप एक अतिरिक्त अक्ष कैसे है। हम आयामों को पुनर्व्यवस्थित कर सकते हैं और 16 श्रृंखलाओं के लिए अक्ष प्राप्त करने के लिए उन्हें समतल कर सकते हैं।

states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])

fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()

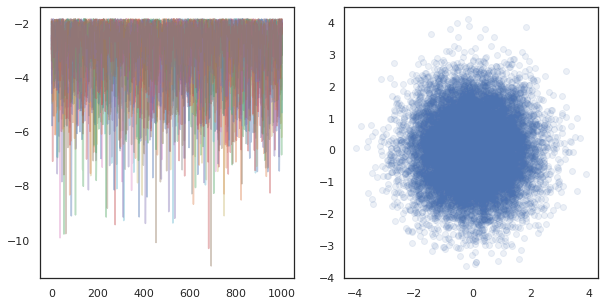
जब कई उपकरणों पर स्वतंत्र चेन चल रहा है, यह जितना आसान है pmap एक समारोह है कि का उपयोग करता है से अधिक आईएनजी tfp.mcmc , यह सुनिश्चित हम एक डिवाइस के लिए यादृच्छिक बीज के लिए अलग मान गुजरती हैं।

डेटा साझा करना

जब हम एमसीएमसी करते हैं, तो लक्ष्य वितरण अक्सर एक डेटासेट पर कंडीशनिंग द्वारा प्राप्त एक पश्च वितरण होता है, और एक असामान्य लॉग-घनत्व की गणना में प्रत्येक देखे गए डेटा के लिए संभावनाओं का योग शामिल होता है।

बहुत बड़े डेटासेट के साथ, एक डिवाइस पर एक श्रृंखला चलाना भी निषेधात्मक रूप से महंगा हो सकता है। हालाँकि, जब हमारे पास कई उपकरणों तक पहुँच होती है, तो हम अपने पास उपलब्ध गणना का बेहतर लाभ उठाने के लिए डेटासेट को सभी उपकरणों में विभाजित कर सकते हैं।

हम एक sharded डाटासेट साथ एमसीएमसी क्या करना चाहते हैं, तो हमें यह सुनिश्चित करना unnormalized लॉग-घनत्व हम प्रत्येक डिवाइस पर गणना की कुल यानि वे डेटा पर घनत्व का प्रतिनिधित्व करता है की जरूरत है, अन्यथा प्रत्येक डिवाइस के लिए अपने स्वयं गलत लक्ष्य के साथ एमसीएमसी कर रही होगी वितरण। इस उद्देश्य से, TFP अब (यानी नए उपकरण है tfp.experimental.distribute और tfp.experimental.mcmc ) कि कंप्यूटिंग "sharded" लॉग संभावनाओं सक्षम है और उनके साथ एमसीएमसी कर।

साझा वितरण

कोर अमूर्त TFP अब कंप्यूटिंग sharded लॉग probabiliities है के लिए प्रदान करता Sharded मेटा-वितरण, जो इनपुट के रूप में एक वितरण लेता है और एक नया वितरण जब एक SPMD संदर्भ में निष्पादित विशिष्ट गुण होते हैं कि देता है। Sharded में जीवन tfp.experimental.distribute ।

Intuitively, एक Sharded यादृच्छिक चर का एक सेट है कि सभी डिवाइस में "विभाजन" किया गया है वितरण मेल खाती है। प्रत्येक डिवाइस पर, वे अलग-अलग नमूने तैयार करेंगे, और व्यक्तिगत रूप से अलग-अलग लॉग-घनत्व हो सकते हैं। वैकल्पिक रूप से, एक Sharded एक "थाली" चित्रमय मॉडल की भाषा में, जहां प्लेट आकार उपकरणों की संख्या है करने के लिए वितरण मेल खाती है।

एक नमूना Sharded वितरण

हम एक से नमूना तो Normal एक कार्यक्रम किया जा रहा है में वितरण pmap प्रत्येक डिवाइस पर एक ही बीज का उपयोग एड, हम प्रत्येक डिवाइस पर ही नमूना मिल जाएगा। हम निम्नलिखित फ़ंक्शन को एक एकल यादृच्छिक चर के नमूने के रूप में सोच सकते हैं जो सभी उपकरणों में सिंक्रनाइज़ है।

# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
  return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                    -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32)

अगर हम लपेट tfd.Normal(0., 1.) एक साथ tfed.Sharded , हम तार्किक अब आठ अलग-अलग यादृच्छिक परिवर्तनीय है (प्रत्येक डिवाइस पर एक) और इसलिए एक ही बीज में गुजर के बावजूद हर एक के लिए एक अलग नमूना उत्पादन करेगा, .

def f(seed, _):
  return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([ 1.2152631 ,  0.7818249 ,  0.32549605,  0.6828047 ,
                     1.3973192 , -0.57830244,  0.37862757,  2.7706041 ],                   dtype=float32)

एक उपकरण पर इस वितरण का एक समान प्रतिनिधित्व सिर्फ 8 स्वतंत्र सामान्य नमूने हैं। हालांकि नमूने के मूल्य अलग होगा ( tfed.Sharded छद्म यादृच्छिक संख्या पीढ़ी कुछ अलग ढंग से करता है), वे दोनों एक ही वितरण प्रतिनिधित्व करते हैं।

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))

DeviceArray([ 0.08086783, -0.38624594, -0.3756545 ,  1.668957  ,
             -1.2758069 ,  2.1192007 , -0.85821325,  1.1305912 ],            dtype=float32)

एक का लॉग घनत्व लेना Sharded वितरण

आइए देखें कि क्या होता है जब हम एक एसपीएमडी संदर्भ में एक नियमित वितरण से नमूने के लॉग-घनत्व की गणना करते हैं।

def f(seed, _):
  dist = tfd.Normal(0., 1.)
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                     -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32),
 ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
                     -0.94012403, -0.94012403, -0.94012403, -0.94012403],                   dtype=float32))

प्रत्येक उपकरण पर प्रत्येक नमूना समान होता है, इसलिए हम प्रत्येक उपकरण पर भी समान घनत्व की गणना करते हैं। सहज रूप से, यहाँ हमारे पास केवल एक सामान्य रूप से वितरित चर पर वितरण है।

एक साथ Sharded वितरण, हम इसलिए जब हम गणना 8 यादृच्छिक परिवर्तनीय पर एक वितरण है, log_prob एक नमूने की, हम योग सभी डिवाइस में, व्यक्तिगत लॉग घनत्व में से प्रत्येक पर। (आप देख सकते हैं कि यह कुल log_prob मान ऊपर परिकलित सिंगलटन log_prob से बड़ा है।)

def f(seed, _):
  dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
    random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)

Sample: [ 1.2152631   0.7818249   0.32549605  0.6828047   1.3973192  -0.57830244
  0.37862757  2.7706041 ]
Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205
 -13.7349205 -13.7349205]

समतुल्य, "अनशेयर्ड" वितरण समान लॉग घनत्व उत्पन्न करता है।

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)

DeviceArray(-13.7349205, dtype=float32)

एक Sharded वितरण से विभिन्न मूल्यों का उत्पादन sample प्रत्येक डिवाइस पर है, लेकिन के लिए एक ही मूल्य प्राप्त log_prob प्रत्येक डिवाइस पर। यहाँ क्या हो रहा है? एक Sharded वितरण एक करता है psum सुनिश्चित करने के लिए आंतरिक रूप से log_prob मूल्यों उपकरणों समन्वयन में कर रहे हैं। हम यह व्यवहार क्यों चाहेंगे? हम प्रत्येक डिवाइस पर एक ही एमसीएमसी श्रृंखला चला रहे हैं, हम चाहते हैं target_log_prob , प्रत्येक डिवाइस में एक ही होने के लिए भले ही गणना में कुछ यादृच्छिक चर सभी डिवाइस में sharded कर रहे हैं।

इसके अतिरिक्त, एक Sharded वितरण सुनिश्चित करें कि सभी डिवाइस में ढ़ाल सही हैं, एच एम सी की तरह है कि एल्गोरिदम, जो संक्रमण समारोह के हिस्से के रूप लॉग-घनत्व समारोह की ढ़ाल लेते हैं, उचित नमूनों का उत्पादन सुनिश्चित करने के लिए।

Sharded JointDistribution रों

हम कई के साथ मॉडल बना सकते हैं Sharded का उपयोग करके यादृच्छिक परिवर्तनीय JointDistribution रों (जेडी)। दुर्भाग्य से, Sharded वितरण सुरक्षित रूप से साथ वेनिला इस्तेमाल किया नहीं किया जा सकता tfd.JointDistribution है, लेकिन tfp.experimental.distribute निर्यात "समझौता" जेडी कि तरह व्यवहार करेगा Sharded वितरण।

def f(seed, _):
  dist = tfed.JointDistributionSequential([
    tfd.Normal(0., 1.),
    tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
  ])
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
                      1.6121525, 1.6121525, 1.6121525], dtype=float32),
  ShardedDeviceArray([ 0.8690128 , -0.83167845,  1.2209264 ,  0.88412696,
                       0.76478404, -0.66208494, -0.0129658 ,  0.7391483 ],                   dtype=float32)],
 ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
                     -12.214451, -12.214451, -12.214451, -12.214451],                   dtype=float32))

ये sharded जेडी दोनों हो सकते हैं Sharded घटक के रूप में और वेनिला TFP वितरण। शार्प न किए गए वितरण के लिए, हम प्रत्येक डिवाइस पर एक ही नमूना प्राप्त करते हैं, और शार्प किए गए वितरण के लिए, हमें अलग-अलग नमूने मिलते हैं। log_prob प्रत्येक डिवाइस पर अच्छी तरह से सिंक्रनाइज़ है।

साथ एमसीएमसी Sharded वितरण

हम के बारे में कैसा लगता है Sharded एमसीएमसी के संदर्भ में वितरण? हम एक उत्पादक मॉडल है कि एक के रूप में व्यक्त किया जा सकता है, तो JointDistribution , हम भर में "ठीकरा" करने के लिए है कि मॉडल से कुछ अक्ष चुन सकते हैं। आम तौर पर, मॉडल में एक यादृच्छिक चर देखे गए डेटा के अनुरूप होगा, और यदि हमारे पास एक बड़ा डेटासेट है जिसे हम सभी उपकरणों में विभाजित करना चाहते हैं, तो हम चाहते हैं कि डेटा बिंदुओं से जुड़े वेरिएबल को भी शार्प किया जाए। हमारे पास "स्थानीय" यादृच्छिक चर भी हो सकते हैं जो एक-से-एक हैं और हम उन टिप्पणियों के साथ हैं जिन्हें हम शार्प कर रहे हैं, इसलिए हमें उन यादृच्छिक चर को अतिरिक्त रूप से शार्प करना होगा।

हम के उपयोग के उदाहरण पर नज़र डालेंगे Sharded इस खंड में TFP एमसीएमसी के साथ वितरण। हम एक सरल बायेसियन रसद प्रतिगमन उदाहरण के साथ शुरू करते हैं, और एक मैट्रिक्स गुणन उदाहरण के साथ समाप्त, कुछ उपयोग-मामले प्रदर्शन करने के लिए के लक्ष्य के साथ करेंगे distribute पुस्तकालय।

उदाहरण: MNIST . के लिए बायेसियन लॉजिस्टिक रिग्रेशन

हम एक बड़े डेटासेट पर बायेसियन लॉजिस्टिक रिग्रेशन करना चाहते हैं; मॉडल एक पूर्व है \(p(\theta)\) प्रतिगमन वजन से अधिक है, और एक संभावना \(p(y_i | \theta, x_i)\) कि सभी डेटा पर अभिव्यक्त किया जाता है \(\{x_i, y_i\}_{i = 1}^N\) कुल संयुक्त लॉग घनत्व प्राप्त करने के लिए। हम अपने डेटा ठीकरा, तो हम मनाया यादृच्छिक परिवर्तनीय ठीकरा था \(x_i\) और \(y_i\) हमारे मॉडल में।

हम MNIST वर्गीकरण के लिए निम्नलिखित बायेसियन लॉजिस्टिक रिग्रेशन मॉडल का उपयोग करते हैं:

\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]

आइए TensorFlow डेटासेट का उपयोग करके MNIST को लोड करें।

mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.

raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.

Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1...
WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your
local data directory. If you'd instead prefer to read directly from our public
GCS bucket (recommended if you're running on GCP), you can instead pass
`try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`.
HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio…
Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.

हमारे पास 60000 प्रशिक्षण छवियां हैं लेकिन आइए हमारे 8 उपलब्ध कोर का लाभ उठाएं और इसे 8 तरीकों से विभाजित करें। हम इस काम के लिए इस्तेमाल करेंगे shard उपयोगिता कार्य करते हैं।

def shard_value(x):
  x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
  return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices

shard = functools.partial(jax.tree_map, shard_value)

sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)

(8, 7500, 784) (8, 7500)

इससे पहले कि हम आगे बढ़ें, आइए शीघ्रता से टीपीयू पर सटीकता और एचएमसी पर इसके प्रभाव पर चर्चा करें। Tpus कम का उपयोग कर मैट्रिक्स गुणा निष्पादित bfloat16 गति के लिए सटीक। bfloat16 मैट्रिक्स गुणा अक्सर कई गहरी सीखने अनुप्रयोगों के लिए पर्याप्त हैं, लेकिन जब एच एम सी के साथ प्रयोग किया है, हम अनुभव पाया है कम सटीक प्रक्षेप पथ भिन्नता वाली, अस्वीकृति के कारण हो सकता है। हम कुछ अतिरिक्त गणना की कीमत पर उच्च परिशुद्धता मैट्रिक्स गुणन का उपयोग कर सकते हैं।

हमारे matmul परिशुद्धता बढ़ाने के लिए, हम उपयोग कर सकते हैं jax.default_matmul_precision साथ डेकोरेटर "tensorfloat32" परिशुद्धता (भी उच्च परिशुद्धता के लिए हम इस्तेमाल कर सकते हैं "float32" परिशुद्धता)।

चलो अब हमारे परिभाषित करते run समारोह है, जो एक यादृच्छिक बीज में ले जाएगा (जो प्रत्येक डिवाइस पर ही होगा) और MNIST की एक ठीकरा। फ़ंक्शन उपरोक्त मॉडल को लागू करेगा और फिर हम एकल श्रृंखला चलाने के लिए TFP की वैनिला MCMC कार्यक्षमता का उपयोग करेंगे। हमें यकीन है कि सजाने के लिए बनाती हूँ run के साथ jax.default_matmul_precision हालांकि नीचे विशिष्ट उदाहरण में, हम बस के रूप में अच्छी तरह से इस्तेमाल कर सकते हैं यकीन है कि आव्यूह गुणन उच्च परिशुद्धता के साथ चलाया जाता है बनाने के लिए डेकोरेटर, jnp.dot(images, w, precision=lax.Precision.HIGH)

# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device. 
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
  images, labels = data # a sharded dataset
  num_examples, dim = images.shape
  num_classes = 10

  def model_fn():
    w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
    b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
    logits = jnp.dot(images, w) + b
    yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
                       shard_axis_name='data')
  model = tfed.JointDistributionCoroutine(model_fn)

  init_seed, sample_seed = random.split(seed)

  initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`

  def target_log_prob(*state):
    return model.log_prob((*state, labels))

  def accuracy(w, b):
    logits = images.dot(w) + b
    preds = logits.argmax(axis=-1)
    # We take the average accuracy across devices by using `lax.pmean`
    return lax.pmean((preds == labels).mean(), 'data')

  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
  kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
  def trace_fn(state, pkr):
    return (
        target_log_prob(*state),
        accuracy(*state),
        pkr.new_step_size)
  states, trace = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    current_state=initial_state,
    kernel=kernel,
    trace_fn=trace_fn,
    seed=sample_seed
  )
  return states, trace

jax.pmap एक JIT संकलन शामिल है, लेकिन संकलित समारोह पहली कॉल के बाद कैश किया गया है। हम फोन करता हूँ run और उत्पादन संकलन कैश करने के लिए ध्यान न दें।

%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s
Wall time: 1min 54s

अब हम फोन करता हूँ run फिर से देखने के लिए कितनी देर तक वास्तविक निष्पादन लेता है।

%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s
Wall time: 1min 43s

हम 200,000 छलांग चरणों को क्रियान्वित कर रहे हैं, जिनमें से प्रत्येक संपूर्ण डेटासेट पर एक ढाल की गणना करता है। गणना को 8 कोर में विभाजित करने से हम लगभग 95 सेकंड में 200,000 युगों के प्रशिक्षण के बराबर की गणना कर सकते हैं, लगभग 2,100 युग प्रति सेकंड!

आइए प्रत्येक नमूने के लॉग-घनत्व और प्रत्येक नमूने की सटीकता को प्लॉट करें:

fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()

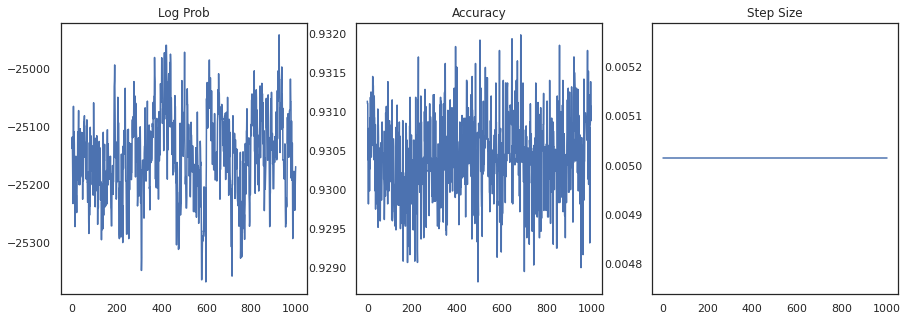
यदि हम नमूनों को जोड़ते हैं, तो हम अपने प्रदर्शन को बेहतर बनाने के लिए बायेसियन मॉडल औसत की गणना कर सकते हैं।

@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
  images, labels = data
  logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
  probs = jax.nn.softmax(logits, axis=-1)
  bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
  avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
  return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')

sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')

Average Accuracy: 0.9188529253005981
BMA Accuracy: 0.9264000058174133
Accuracy Improvement: 0.0075470805168151855

एक बायेसियन मॉडल औसत हमारी सटीकता को लगभग 1% बढ़ा देता है!

उदाहरण: MovieLens अनुशंसा प्रणाली

आइए अब MovieLens अनुशंसा डेटासेट के साथ अनुमान लगाने का प्रयास करें, जो उपयोगकर्ताओं का एक संग्रह है और विभिन्न फिल्मों की उनकी रेटिंग है। विशेष रूप से, हम एक के रूप में MovieLens प्रतिनिधित्व कर सकते हैं \(N \times M\) घड़ी मैट्रिक्स \(W\) जहां \(N\) उपयोगकर्ताओं और की संख्या है \(M\) फिल्मों की संख्या है, हम उम्मीद करते हैं \(N > M\)। की प्रविष्टियों \(W_{ij}\) एक बूलियन का संकेत है या नहीं, उपयोगकर्ता हैं \(i\) देखा फिल्म \(j\)। ध्यान दें कि MovieLens उपयोगकर्ता रेटिंग प्रदान करता है, लेकिन हम समस्या को सरल बनाने के लिए उनकी उपेक्षा कर रहे हैं।

सबसे पहले, हम डेटासेट लोड करेंगे। हम 1 मिलियन रेटिंग वाले संस्करण का उपयोग करेंगे।

movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
          'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
          'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
          'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']

Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0...
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl…

HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value='')))
Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord
HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value='')))
Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.

हम घड़ी मैट्रिक्स प्राप्त करने के लिए डाटासेट में से कुछ पूर्व प्रसंस्करण करूँगा \(W\)।

raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']

movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])

num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1

movie_titles = dict(zip(movielens['train']['movie_id'],
                        movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
                        genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
                     for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]

watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)

(6040, 3706)

हम के लिए एक उत्पादक मॉडल को परिभाषित कर सकते \(W\), एक सरल संभाव्य मैट्रिक्स गुणन मॉडल का उपयोग। हम एक अव्यक्त मान \(N \times D\) उपयोगकर्ता मैट्रिक्स \(U\) और एक अव्यक्त \(M \times D\) फिल्म मैट्रिक्स \(V\), जो जब गुणा घड़ी मैट्रिक्स के लिए एक Bernoulli की logits उत्पादन \(W\)। हम यह भी उपयोगकर्ताओं और फिल्मों, के लिए एक पूर्वाग्रह वैक्टर शामिल करेंगे \(u\) और \(v\)।

\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]

यह एक बहुत बड़ा मैट्रिक्स है; 6040 उपयोगकर्ता और 3706 फिल्में 22 मिलियन से अधिक प्रविष्टियों के साथ एक मैट्रिक्स की ओर ले जाती हैं। हम इस मॉडल को शार्प करने के लिए कैसे संपर्क करते हैं? ठीक है, अगर हम मान लेते हैं कि \(N > M\) (फिल्मों की तुलना में अधिक उपयोगकर्ता हैं यानी), तो यह समझ बनाने हैं उपयोगकर्ता अक्ष भर में घड़ी मैट्रिक्स ठीकरा है, इसलिए प्रत्येक डिवाइस उपयोगकर्ताओं के एक सबसेट के लिए इसी घड़ी मैट्रिक्स का एक हिस्सा होता है . पिछले उदाहरण के विपरीत, तथापि, हम भी ऊपर ठीकरा करना होगा \(U\) मैट्रिक्स, क्योंकि यह प्रत्येक उपयोगकर्ता के लिए एक एम्बेड है, तो प्रत्येक डिवाइस के ठीकरा के लिए जिम्मेदार होगा \(U\) और की एक ठीकरा \(W\). दूसरी ओर, \(V\) unsharded हो जाएगा और उपकरणों में सिंक्रनाइज़ किया।

sharded_watch_matrix = shard(watch_matrix)

इससे पहले कि हम हमारे बारे में run , चलो जल्दी से स्थानीय यादृच्छिक चर sharding साथ अतिरिक्त चुनौतियों पर चर्चा करते हैं \(U\)। जब एच एम सी, वेनिला चल tfp.mcmc.HamiltonianMonteCarlo गिरी नमूना होगा श्रृंखला के राज्य के प्रत्येक तत्व के लिए momenta। पहले, केवल अनशेल्ड रैंडम वेरिएबल ही उस स्थिति का हिस्सा थे, और प्रत्येक डिवाइस पर मोमेंटा समान था। अब हम एक sharded जब \(U\), हम के लिए प्रत्येक डिवाइस पर अलग momenta नमूने के लिए की जरूरत है \(U\)के लिए एक ही momenta नमूने जबकि, \(V\)। इसे पूरा करने के हम उपयोग कर सकते हैं tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo एक साथ Sharded गति वितरण। जैसा कि हम समानांतर गणना को प्रथम श्रेणी बनाना जारी रखते हैं, हम इसे सरल बना सकते हैं, उदाहरण के लिए एचएमसी कर्नेल में एक शार्पनेस इंडिकेटर लेकर।

def make_run(*,
             axis_name,
             dim=20,
             num_chains=2,
             prior_variance=1.,
             step_size=1e-2,
             num_leapfrog_steps=100,
             num_burnin_steps=1000,
             num_results=500,
             ):
  @functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
  @jax.default_matmul_precision('tensorfloat32')
  def run(key, watch_matrix):
    num_users, num_movies = watch_matrix.shape

    Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)

    def prior_fn():
      user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
      user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
      movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
      movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
      return (user_embeddings, user_bias, movie_embeddings, movie_bias)
    prior = tfed.JointDistributionCoroutine(prior_fn)

    def model_fn():
      user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
      logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
                + user_bias[..., :, None] + movie_bias[..., None, :])
      yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
    model = tfed.JointDistributionCoroutine(model_fn)

    init_key, sample_key = random.split(key)
    initial_state = prior.sample(seed=init_key, sample_shape=num_chains)

    def target_log_prob(*state):
      return model.log_prob((*state, watch_matrix))

    momentum_distribution = tfed.JointDistributionSequential([
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
    ])

    # We pass in momentum_distribution here to ensure that the momenta for 
    # user_embeddings and user_bias are also sharded
    kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
                                                      num_leapfrog_steps,
                                                      momentum_distribution=momentum_distribution)

    num_adaptation_steps = int(0.8 * num_burnin_steps)
    kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)

    def trace_fn(state, pkr):
      return {
        'log_prob': target_log_prob(*state),
        'log_accept_ratio': pkr.inner_results.log_accept_ratio,
      }
    return tfm.sample_chain(
        num_results, initial_state,
        kernel=kernel,
        num_burnin_steps=num_burnin_steps,
        trace_fn=trace_fn,
        seed=sample_key)
  return run

संकलित कैश करने के लिए एक बार हम फिर से इसे चलाने जाएगा run ।

%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 56 s, sys: 1min 24s, total: 2min 20s
Wall time: 3min 35s

अब हम इसे कंपाइलेशन ओवरहेड के बिना फिर से चलाएंगे।

%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s
Wall time: 3min 1s

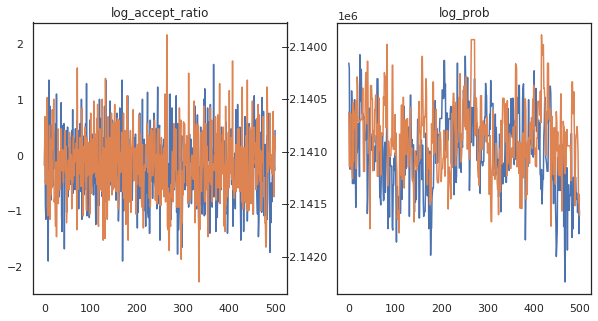
ऐसा लगता है कि हमने लगभग 3 मिनट में लगभग 150,000 छलांग के चरण पूरे कर लिए हैं, इसलिए प्रति सेकंड लगभग 83 छलांग लगाने वाले कदम! आइए हमारे नमूनों के स्वीकार्य अनुपात और लॉग घनत्व को प्लॉट करें।

fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
  ax.plot(val[0]) # Indexing into a sharded array, each element is the same
  ax.set_title(key);

अब जब हमारे पास हमारी मार्कोव श्रृंखला से कुछ नमूने हैं, तो आइए कुछ भविष्यवाणियां करने के लिए उनका उपयोग करें। सबसे पहले, आइए प्रत्येक घटक को निकालें। याद रखें कि user_embeddings और user_bias , डिवाइस भर में विभाजित कर रहे हैं इसलिए हम अपने को श्रेणीबद्ध करने की जरूरत है ShardedArray उन सब को प्राप्त करने के लिए। दूसरी ओर, movie_embeddings और movie_bias हर डिवाइस पर ही कर रहे हैं, तो हम सिर्फ पहली ठीकरा से मूल्य चुन सकते हैं। हम नियमित रूप से इस्तेमाल करेंगे numpy सीपीयू को tpus पीछे से मूल्यों की प्रतिलिपि बनाने के।

user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')

User embeddings: (500, 2, 6040, 20)
User bias: (500, 2, 6040)
Movie embeddings: (500, 2, 3706, 20)
Movie bias: (500, 2, 3706)

आइए एक सरल अनुशंसा प्रणाली बनाने का प्रयास करें जो इन नमूनों में पकड़ी गई अनिश्चितता का उपयोग करती है। आइए पहले एक फ़ंक्शन लिखें जो फिल्मों को घड़ी की संभावना के अनुसार रैंक करता है।

@jax.jit
def recommend(sample, user_id):
  user_embeddings, user_bias, movie_embeddings, movie_bias = sample
  movie_logits = (
      jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
      + user_bias[user_id] + movie_bias)
  return movie_logits.argsort()[::-1]

अब हम एक फ़ंक्शन लिख सकते हैं जो सभी नमूनों पर लूप करता है और प्रत्येक के लिए, शीर्ष रैंक वाली फिल्म चुनता है जिसे उपयोगकर्ता ने पहले नहीं देखा है। फिर हम नमूनों में सभी अनुशंसित फिल्मों की संख्या देख सकते हैं।

def get_recommendations(user_id): 
  movie_ids = []
  already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
  for i in range(500):
    for j in range(2):
      sample = jax.tree_map(lambda x: x[i, j], samples)
      ranking = recommend(sample, user_id)
      for movie_id in ranking:
        if int(movie_id) not in already_watched:
          movie_ids.append(movie_id)
          break
  return movie_ids

def plot_recommendations(movie_ids, ax=None):
  titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
  ax = ax or plt.gca()
  names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
  ax.bar(names, counts)
  ax.set_xticklabels(names, rotation=90)

आइए उस उपयोगकर्ता को लें जिसने सबसे अधिक फिल्में देखी हैं बनाम जिसने सबसे कम देखी है।

user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])

2314 20

हम अपने सिस्टम के बारे में अधिक निश्चितता है आशा user_most से user_least , यह देखते हुए कि हम क्या फिल्मों में से सॉर्ट करता बारे में अधिक जानकारी है कि user_most अधिक देखने के लिए की संभावना है।

fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');

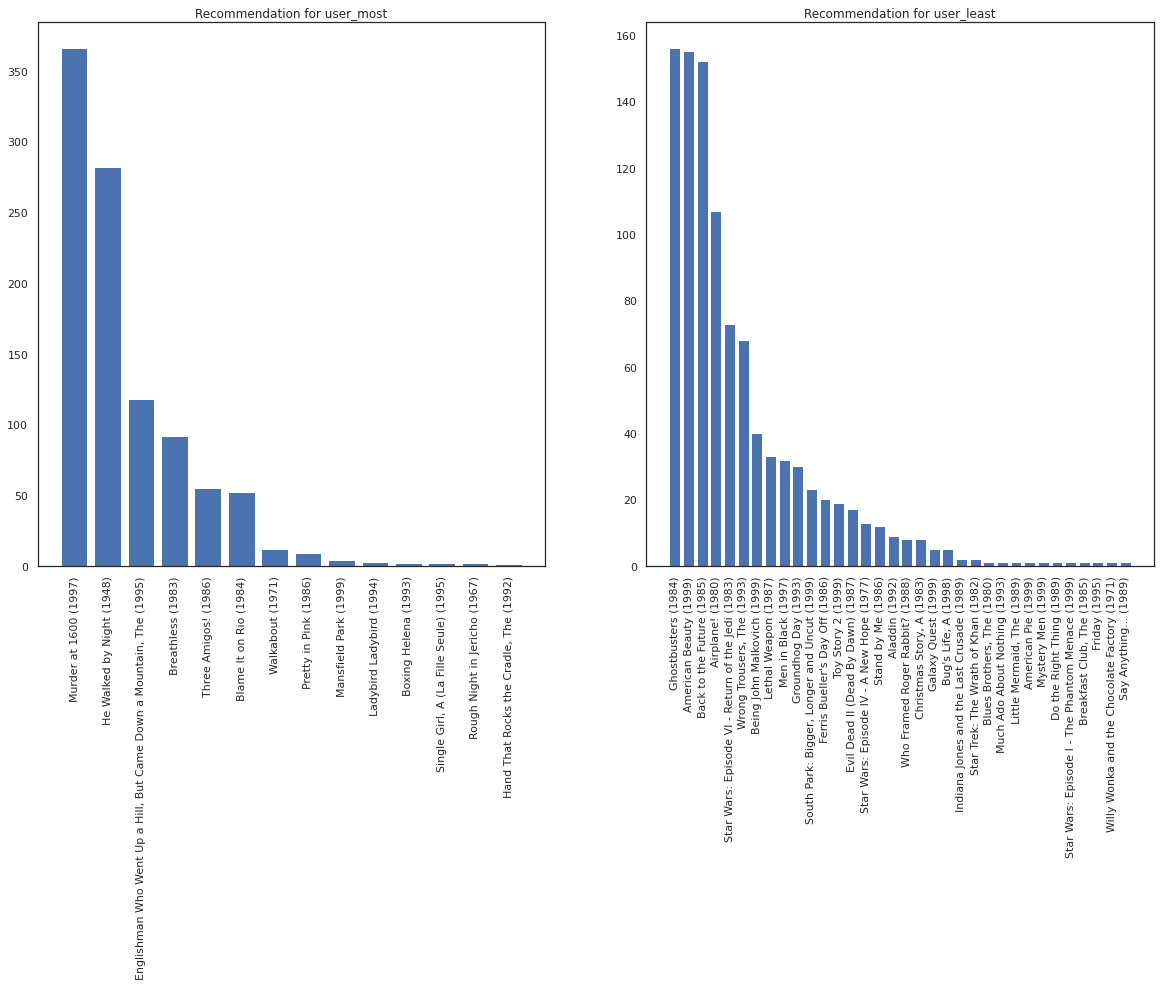
हम के लिए हमारे सुझावों में अधिक विचरण है कि वहाँ देख user_least उनकी घड़ी वरीयताओं में हमारे अतिरिक्त अनिश्चितता को दर्शाती है।

हम अनुशंसित फिल्मों की शैलियों को भी देख सकते हैं।

most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');

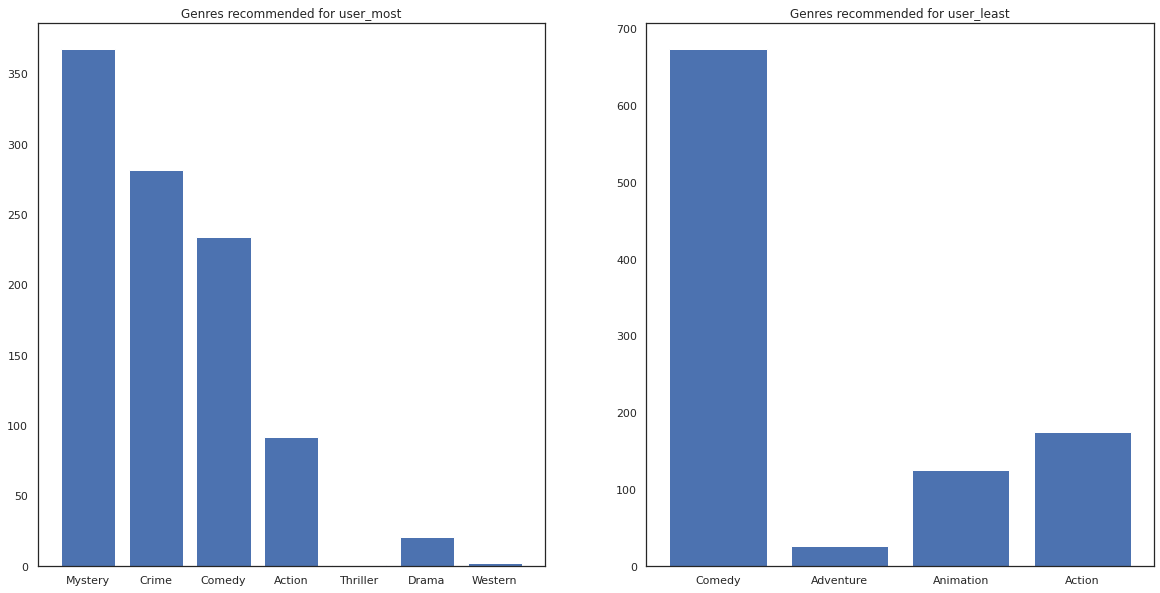
user_most फिल्मों का एक बहुत कुछ देखा है और रहस्य और अपराध की तरह अधिक आला शैलियों सिफारिश की गई है, जबकि user_least कई फिल्मों में देखा नहीं किया गया है और अधिक मुख्यधारा सिनेमा, जो तिरछा कॉमेडी और एक्शन की सिफारिश की थी।