הצג באתר TensorFlow.org

הפעל בגוגל קולאב

צפה במקור ב-GitHub

הורד מחברת

TensorFlow Probability (TFP) ב-JAX כולל כעת כלים עבור מחשוב נומרי מבוזר. כדי להרחיב למספרים גדולים של מאיצים, הכלים בנויים סביב כתיבת קוד תוך שימוש בפרדיגמת "מספר נתונים של תוכנית יחידה", או בקיצור SPMD.

במחברת זו, נעבור על איך "לחשוב ב-SPMD" ונציג את ההפשטות החדשות של TFP לשינוי קנה מידה לתצורות כגון תרמילים של TPU, או אשכולות של GPUs. אם אתה מפעיל את הקוד הזה בעצמך, הקפד לבחור זמן ריצה של TPU.

נתקין תחילה את הגרסאות האחרונות TFP, JAX ו-TF.

מתקין

pip install jaxlib --upgrade -q 2>&1 1> /dev/null
pip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/null
pip install tf-nightly-cpu -q -I 2>&1 1> /dev/null
pip install jax -I -q --upgrade 2>&1 1>/dev/null

נייבא כמה ספריות כלליות, יחד עם כמה כלי עזר של JAX.

הגדרה וייבוא

import functools
import collections
import contextlib

import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds

from tensorflow_probability.substrates import jax as tfp

sns.set(style='white')

INFO:tensorflow:Enabling eager execution
INFO:tensorflow:Enabling v2 tensorshape
INFO:tensorflow:Enabling resource variables
INFO:tensorflow:Enabling tensor equality
INFO:tensorflow:Enabling control flow v2

אנחנו גם נגדיר כמה כינויי TFP שימושיים. האבסטרקטית החדשה ניתנת כיום tfp.experimental.distribute ו tfp.experimental.mcmc .

tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc

Root = tfed.JointDistributionCoroutine.Root

כדי לחבר את המחברת ל-TPU, אנו משתמשים בעוזר הבא מ-JAX. כדי לאשר שאנחנו מחוברים, אנו מדפיסים את מספר המכשירים, שאמור להיות שמונה.

from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')

Found 8 devices

למבוא קצר jax.pmap

לאחר חיבור TPU, יש לנו גישה שמונה מכשירים. עם זאת, כאשר אנו מריצים קוד JAX בשקיקה, ברירת המחדל של JAX היא הפעלת חישובים על אחד בלבד.

הדרך הפשוטה ביותר לביצוע חישוב על פני מכשירים רבים היא מיפוי של פונקציה, כאשר כל מכשיר יבצע אינדקס אחד של המפה. JAX מספק את jax.pmap ( "המפה מקבילה") טרנספורמציה אשר הופך פונקציה לתוך אחד הממפה את הפונקציה בכמה מכשירים.

בדוגמה הבאה, אנו יוצרים מערך בגודל 8 (כדי להתאים למספר המכשירים הזמינים) וממפים פונקציה שמוסיפה 5 על פניו.

xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)

<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5.  6.  7.  8.  9. 10. 11. 12.]

הערה שנקבל ShardedDeviceArray בחזרה סוג, המציין כי מערך התפוקה מפוצל פיזית בין מכשירים שונים.

jax.pmap מעשים סמנטיים כמו מפה, אבל יש כמה אפשרויות חשוב שמשנות את ההתנהגות שלה. כברירת מחדל, pmap מניחה כול תשומות לפונקציה שמתבצעות ממופה מעל, אבל אנחנו יכולים לשנות התנהגות זו עם in_axes הטיעון.

xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)

[ 5.  6.  7.  8.  9. 10. 11. 12.]

בדומה לכך, את out_axes טיעון כדי pmap קובע אם להחזיר את הערכים על כל מכשיר. הגדרת out_axes כדי None אוטומטית מחזירה את הערך על מכשיר ה -1 ויש להשתמש רק אם אנחנו בטוחים הערכים הם זהים בכל מכשיר.

xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)

2.0

מה קורה כאשר מה שהיינו רוצים לעשות לא ניתן לביטוי בקלות כפונקציה טהורה ממופה? לדוגמה, מה אם נרצה לעשות סכום על פני הציר שעליו אנו ממפים? JAX מציעה "קולקטיבים", פונקציות המתקשרות בין מכשירים, כדי לאפשר כתיבת תוכניות מבוזרות מעניינות ומורכבות יותר. כדי להבין איך בדיוק הם עובדים, נציג את SPMD.

מה זה SPMD?

מספר נתונים של תוכנית יחידה (SPMD) הוא מודל תכנות בו-זמנית שבו תוכנית בודדת (כלומר אותו קוד) מבוצעת בו-זמנית על פני התקנים, אך הקלט לכל אחת מהתוכניות הפועלות עשויות להיות שונות.

אם התוכנית שלנו היא פונקציה פשוטה של תשומות שלה (כלומר משהו כמו x + 5 ), הרצת תוכנית ב SPMD הוא פשוט מיפוי זה נתונים שונים על פני, כמו שעשינו עם jax.pmap קודם לכן. עם זאת, אנחנו יכולים לעשות יותר מסתם "מפה" פונקציה. JAX מציעה "קולקטיבים", שהם פונקציות המתקשרות בין מכשירים.

לדוגמה, אולי נרצה לקחת סכום של כמות בכל המכשירים שלנו. לפני שאנחנו עושים את זה, אנחנו צריכים להקצות שם הציר אנו מיפוי אתם מעל ב pmap . אנחנו מכן להשתמש lax.psum ( "סכום מקביל") הפונקציה לבצע סכום במכשירים שונים, הבטחת לנו לזהות את שמו ציר שאנחנו המסכם מעל.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)

ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)

psum קולקטיבית אגרגטים הערך של x על כל מכשיר ומסנכרן הערך שלה ברחבי המפה כלומר out הוא 28. על כל מכשיר. אנחנו כבר לא מבצעים "מפה" פשוטה, אלא אנחנו מפעילים תוכנית SPMD שבה החישוב של כל מכשיר יכול כעת לקיים אינטראקציה עם אותו חישוב במכשירים אחרים, אם כי בצורה מוגבלת באמצעות קולקטיבים. בתרחיש זה, אנו יכולים להשתמש out_axes = None , כי psum יסנכרן את הערך.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))

ShardedDeviceArray(28., dtype=float32)

SPMD מאפשר לנו לכתוב תוכנית אחת המופעלת על כל מכשיר בכל תצורת TPU בו-זמנית. אותו קוד המשמש ללימוד מכונה על 8 ליבות TPU יכול לשמש על פוד TPU שעשוי להכיל מאות עד אלפי ליבות! לקבלת הדרכה מפורטת יותר על jax.pmap ו SPMD, אתה יכול להתייחס אלי הדרכת 101 JAX .

MCMC בקנה מידה

במחברת זו, אנו מתמקדים בשימוש בשיטות Markov Chain Monte Carlo (MCMC) להסקת בייסיאנית. ישנן דרכים עשויות להשתמש במכשירים רבים עבור MCMC, אך במחברת זו נתמקד בשניים:

1. הפעלת רשתות מרקוב עצמאיות במכשירים שונים. המארז הזה הוא די פשוט ואפשר לעשות אותו עם וניל TFP.
2. חלוקת מערך נתונים בין מכשירים. מקרה זה הוא קצת יותר מורכב ודורש מכונות TFP שנוספו לאחרונה.

רשתות עצמאיות

נניח שברצוננו להסיק מסקנות בייסיאניות על בעיה באמצעות MCMC ונרצה להפעיל מספר רשתות במקביל על פני מספר מכשירים (נניח 2 בכל מכשיר). מסתבר שזו תוכנית שאנחנו יכולים פשוט "למפות" על פני מכשירים, כלומר כזו שלא צריכה קולקטיבים. כדי לוודא שכל תוכנית מבצעת שרשרת מרקוב אחרת (בניגוד להרצה של אותה אחת), אנו מעבירים לכל מכשיר ערך שונה עבור הזרע האקראי.

בואו ננסה את זה על בעיית צעצוע של דגימה מהפצה גאוסית דו-ממדית. אנחנו יכולים להשתמש בפונקציונליות ה-MCMC הקיימת של TFP מחוץ לקופסה. באופן כללי, אנו מנסים להכניס את רוב ההיגיון לפונקציה הממפה שלנו כדי להבחין בצורה מפורשת יותר בין מה שרץ בכל המכשירים לעומת רק הראשון.

def run(seed):
  target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob

  initial_state = jnp.zeros([2, 2]) # 2 chains
  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
  def trace_fn(state, pkr):
    return target_log_prob(state)

  states, log_prob = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    kernel=kernel,
    current_state=initial_state,
    trace_fn=trace_fn,
    seed=seed
  )
  return states, log_prob

לכשעצמו, run הפונקציה לוקחת זרע אקראי נתינות (כדי לראות איך עבודה אקראית נתינות, אתה יכול לקרוא את הפריון הכולל על JAX מחברת או לראות את הדרכת JAX 101 ). מיפוי run מעל זרעים שונים יגרום להריץ כמה שרשרות מרקוב עצמאיות.

states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)

(8, 1000, 2, 2) (8, 1000, 2)

שימו לב כיצד יש לנו כעת ציר נוסף המתאים לכל מכשיר. נוכל לסדר מחדש את המידות ולשטח אותן כדי לקבל ציר ל-16 השרשראות.

states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])

fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()

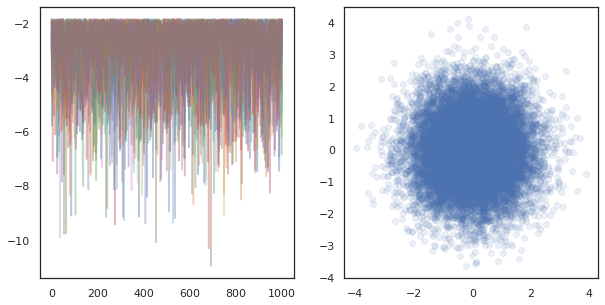
בעת הפעלת רשתות עצמאיות על מכשירים רבים, זה קל כמו pmap -ing מעל פונקציה שימושים tfp.mcmc , הבטחת לנו לעבור ערכים שונים זרע אקראי לכל מכשיר.

שיתוף נתונים

כאשר אנו עושים MCMC, התפלגות המטרה היא לרוב התפלגות אחורית המתקבלת על ידי התניה על מערך נתונים, ומחשוב צפיפות לוג לא מנורמלת כרוך בסיכומו של סבירות לכל נתון שנצפה.

עם מערכי נתונים גדולים מאוד, זה יכול להיות יקר מאוד אפילו להפעיל שרשרת אחת במכשיר בודד. עם זאת, כאשר יש לנו גישה למספר מכשירים, אנו יכולים לפצל את מערך הנתונים על פני המכשירים כדי למנף טוב יותר את המחשוב שיש לנו.

אם היינו רוצים לעשות המרק"ם עם הנתונים sharded, אנחנו צריכים להבטיח את יומן בצפיפות unnormalized אנו מחשבים על כל התקן מייצגת את הכל, כלומר צפיפות מעל כל הנתונים, אחרת כל התקן יעשה המרק"ם עם יעד שגוי משלהם הפצה. לשם כך, הפריון הכולל כעת יש כלים חדשים (כלומר tfp.experimental.distribute ו tfp.experimental.mcmc ) המאפשרים "sharded" הסתברויות יומן מחשוב ועושים המרק"ם איתם.

הפצות מפוצלות

גידול הפריון הכולל הפשטה הליבה מספק כעת לחישוב probabiliities יומן sharded הוא Sharded מטא-הפצה, אשר לוקח הפצה כקלט ומחזירה הפצה חדש כי יש מאפיינים ספציפיים כאשר להורג בהקשר SPMD. Sharded חייהם ב tfp.experimental.distribute .

באופן אינטואיטיבי, A Sharded תואמת החלוקה קבוצה של משתנים אקראיים שהיו "פיצול" בין מכשירים שונים. בכל מכשיר, הם יפיקו דגימות שונות, ויכולות להיות בנפרד צפיפות יומן שונים. לחלופין, Sharded תואמת הפצה "צלחת" בעגת מודל גרפית, שבו גודל הצלחת הוא מספר התקנים.

דגימת Sharded הפצה

אם אנחנו לטעום מן Normal הפצה יצור תוכנית pmap -ed באמצעות אותו זרע על כל מכשיר, נקבל אותו המדגם על כל מכשיר. אנו יכולים לחשוב על הפונקציה הבאה כדגימה של משתנה אקראי יחיד המסונכרן בין מכשירים.

# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
  return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                    -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32)

אם אנו עוטפים tfd.Normal(0., 1.) עם tfed.Sharded , אנו לוגית יש כעת שמונה משתנים אקראיים שונים (אחד על כל מכשיר) ולכן יהיה לייצר מדגם שונה עבור כל אחד, למרות עובר באותו זרע .

def f(seed, _):
  return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([ 1.2152631 ,  0.7818249 ,  0.32549605,  0.6828047 ,
                     1.3973192 , -0.57830244,  0.37862757,  2.7706041 ],                   dtype=float32)

ייצוג שווה ערך של התפלגות זו במכשיר בודד הוא רק 8 דגימות נורמליות עצמאיות. למרות שהערך של המדגם יהיה שונה ( tfed.Sharded עושה הדור מספר פסאודו אקראי מעט שונה), שניהם מייצגים את אותה חלוקה.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))

DeviceArray([ 0.08086783, -0.38624594, -0.3756545 ,  1.668957  ,
             -1.2758069 ,  2.1192007 , -0.85821325,  1.1305912 ],            dtype=float32)

אם תיקח את בצפיפות היומן של Sharded הפצה

בואו נראה מה קורה כאשר אנו מחשבים את צפיפות הלוג של דגימה מהתפלגות רגילה בהקשר SPMD.

def f(seed, _):
  dist = tfd.Normal(0., 1.)
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                     -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32),
 ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
                     -0.94012403, -0.94012403, -0.94012403, -0.94012403],                   dtype=float32))

כל דגימה זהה בכל מכשיר, כך שאנו מחשבים את אותה צפיפות גם בכל מכשיר. באופן אינטואיטיבי, כאן יש לנו רק התפלגות על משתנה יחיד שמתחלק נורמלי.

עם Sharded הפצה, יש לנו הפצה מעל 8 משתנים אקראיים, ולכן כאשר אנו מחשבים את log_prob של מדגם, נסכם, במכשירים שונים, על פני כל אחד צפיפויות יומן הפרט. (ייתכן שתבחין שהערך הכולל הזה של log_prob גדול יותר מהערך הבודד log_prob שחושב למעלה.)

def f(seed, _):
  dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
    random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)

Sample: [ 1.2152631   0.7818249   0.32549605  0.6828047   1.3973192  -0.57830244
  0.37862757  2.7706041 ]
Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205
 -13.7349205 -13.7349205]

ההפצה המקבילה, "לא מרוסקת", מייצרת את אותה צפיפות לוג.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)

DeviceArray(-13.7349205, dtype=float32)

Sharded הפצה מייצרת ערכים שונה sample על כל מכשיר, אלא לקבל אותו ערך עבור log_prob על כל מכשיר. מה קורה כאן? Sharded הפצה עושה psum פנימי כדי להבטיח את log_prob הערכים הם מסונכרנים במכשירים. למה שנרצה את ההתנהגות הזו? אם אנחנו רצים באותו שרשרת המרק"ם על כל מכשיר, היינו רוצים target_log_prob להיות זהה לאורך כל מכשיר, גם אם כמה משתנים אקראיים בחישוב הם sharded במכשירים שונים.

בנוסף, Sharded מבטיחה הפצה הדרגתית בין מכשירים הם נכונים, כדי להבטיח אלגוריתמים כמו HMC, אשר לוקחים הדרגתיות של פונקצית יומן בצפיפות כחלק פונקציית המעבר, לייצר דגימות נכונות.

Sharded JointDistribution ים

אנחנו יכולים ליצור מודלים עם מספר Sharded משתנה אקראי באמצעות JointDistribution הים (JDS). למרבה הצער, Sharded הפצות לא ניתן להשתמש בבטחה עם וניל tfd.JointDistribution ים, אבל tfp.experimental.distribute היצוא "תוקנו" JDS כי יתנהג כמו Sharded הפצות.

def f(seed, _):
  dist = tfed.JointDistributionSequential([
    tfd.Normal(0., 1.),
    tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
  ])
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
                      1.6121525, 1.6121525, 1.6121525], dtype=float32),
  ShardedDeviceArray([ 0.8690128 , -0.83167845,  1.2209264 ,  0.88412696,
                       0.76478404, -0.66208494, -0.0129658 ,  0.7391483 ],                   dtype=float32)],
 ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
                     -12.214451, -12.214451, -12.214451, -12.214451],                   dtype=float32))

JDS sharded אלה יכולות להיות הן Sharded הפצות ווניל הפריון הכולל רכיבים. עבור ההתפלגויות הלא מרוסקות, אנו מקבלים את אותה דגימה בכל מכשיר, ועבור ההפצות המרוסקות, אנו מקבלים דגימות שונות. log_prob על כול מכשיר הוא מסונכרן.

המרק"ם עם Sharded הפצות

איך אפשר לחשוב על Sharded הפצות בהקשר של המרק"ם? אם יש לנו במודל הגנרטיבי שניתן מבוטא JointDistribution , אנחנו יכולים לבחור איזה ציר של שהמודל ל "שבר" על פני. בדרך כלל, משתנה אקראי אחד במודל יתאים לנתונים שנצפו, ואם יש לנו מערך נתונים גדול שברצוננו לפזר בין מכשירים, אנו רוצים שהמשתנים המשויכים לנקודות נתונים יתנפצו גם כן. ייתכן שיש לנו גם משתנים אקראיים "מקומיים" שהם אחד לאחד עם התצפיות שאנו חותכים, אז נצטרך לגזור בנוסף את המשתנים האקראיים האלה.

אנחנו נעבור על דוגמאות של השימוש Sharded הפצות עם הפריון הכולל המרק"ם בסעיף זה. נתחיל עם דוגמה רגרסיה לוגיסטית בייס פשוטה, ולהסיק עם דוגמה לגורמים מטריקס, במטרה להדגים כמה מקרים שבהם השימוש עבור distribute הספרייה.

דוגמה: רגרסיה לוגיסטית בייסיאנית עבור MNIST

ברצוננו לבצע רגרסיה לוגיסטית בייסיאנית על מערך נתונים גדול; יש את הדוגמנית לפני \(p(\theta)\) רחבי משקולות רגרסיה, ועל סבירות \(p(y_i | \theta, x_i)\) כי הוא סיכם על כל הנתונים \(\{x_i, y_i\}_{i = 1}^N\) כדי להשיג צפיפות יומן משותף הכולל. אם אנו שבר הנתונים שלנו, היינו שבר משתנה אקראי הנצפה \(x_i\) ו \(y_i\) במודל שלנו.

אנו משתמשים במודל הרגרסיה הלוגיסטית הבאייסיאנית עבור סיווג MNIST:

\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]

בואו נטען את MNIST באמצעות ערכות נתונים של TensorFlow.

mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.

raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.

Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1...
WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your
local data directory. If you'd instead prefer to read directly from our public
GCS bucket (recommended if you're running on GCP), you can instead pass
`try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`.
HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio…
Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.

יש לנו 60000 תמונות אימון אבל בואו ננצל את 8 הליבות הזמינות שלנו ונחלק אותן ל-8 דרכים. נשתמש שימושי זה shard פונקציית תועלת.

def shard_value(x):
  x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
  return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices

shard = functools.partial(jax.tree_map, shard_value)

sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)

(8, 7500, 784) (8, 7500)

לפני שנמשיך, בואו נדון במהירות בדייקנות ב-TPUs והשפעתו על HMC. TPUs לבצע כפל מטריצות באמצעות נמוכה bfloat16 דיוק עבור מהירות. bfloat16 כפל מטריצות הם בדרך כלל מספיק עבור יישומים רבים למידה עמוקות, אך בעת שימוש עם HMC, אנו אמפיריים מצאנו את הדיוק הנמוך יכול להוביל מסלולי diverging, גרימת דחיות. אנו יכולים להשתמש בכפל מטריצות דיוק גבוה יותר, במחיר של חישוב נוסף.

כדי להגדיל את דיוק matmul שלנו, אנו יכולים להשתמש jax.default_matmul_precision המעצב עם "tensorfloat32" דיוק (אפילו עבור דיוק גבוה שיכולנו להשתמש "float32" דיוק).

בואו עכשיו מגדירים שלנו run הפונקציה, אשר יעביר בתוך זרע אקראי (אשר יהיה זהה על כל מכשיר) וכן שבר של MNIST. הפונקציה תטמיע את המודל הנ"ל ולאחר מכן נשתמש בפונקציונליות הווניל MCMC של TFP כדי להפעיל שרשרת אחת. אנחנו נדאג לקשט run עם jax.default_matmul_precision מעצב כדי לוודא כפל במטריצה מנוהלת עם דיוק גבוה, אם כי בדוגמה מסוימת בהמשך, אנחנו באותה מידה היה יכול להשתמש jnp.dot(images, w, precision=lax.Precision.HIGH) .

# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device. 
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
  images, labels = data # a sharded dataset
  num_examples, dim = images.shape
  num_classes = 10

  def model_fn():
    w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
    b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
    logits = jnp.dot(images, w) + b
    yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
                       shard_axis_name='data')
  model = tfed.JointDistributionCoroutine(model_fn)

  init_seed, sample_seed = random.split(seed)

  initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`

  def target_log_prob(*state):
    return model.log_prob((*state, labels))

  def accuracy(w, b):
    logits = images.dot(w) + b
    preds = logits.argmax(axis=-1)
    # We take the average accuracy across devices by using `lax.pmean`
    return lax.pmean((preds == labels).mean(), 'data')

  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
  kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
  def trace_fn(state, pkr):
    return (
        target_log_prob(*state),
        accuracy(*state),
        pkr.new_step_size)
  states, trace = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    current_state=initial_state,
    kernel=kernel,
    trace_fn=trace_fn,
    seed=sample_seed
  )
  return states, trace

jax.pmap כולל הידור JIT אבל פונקצית ההידור היא במטמון לאחר השיחה הראשונה. אנחנו נתקשר run ולהתעלם הפלט לאפסן את ההידור.

%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s
Wall time: 1min 54s

כעת אנו נתקשר run שוב כדי לראות כמה זמן הביצוע בפועל לוקח.

%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s
Wall time: 1min 43s

אנו מבצעים 200,000 שלבי קפיצת מדרגה, שכל אחד מהם מחשב שיפוע על כל מערך הנתונים. פיצול החישוב על פני 8 ליבות מאפשר לנו לחשב את המקבילה ל-200,000 עידנים של אימון בכ-95 שניות, כ-2,100 עידנים בשנייה!

בואו נשרטט את צפיפות הלוג של כל דגימה ואת הדיוק של כל דגימה:

fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()

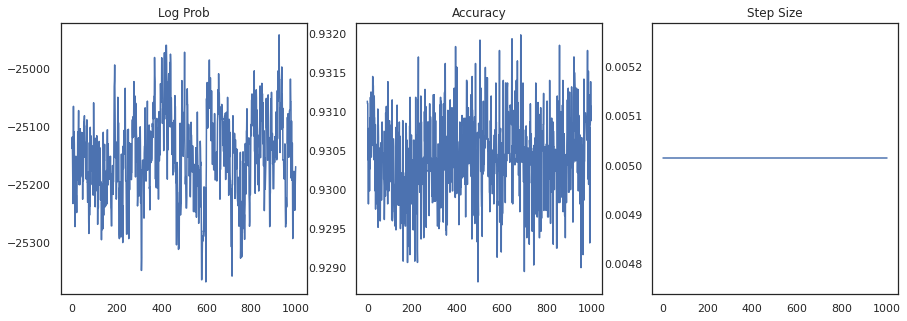
אם נרכיב את הדגימות, נוכל לחשב ממוצע מודל בייסיאני כדי לשפר את הביצועים שלנו.

@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
  images, labels = data
  logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
  probs = jax.nn.softmax(logits, axis=-1)
  bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
  avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
  return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')

sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')

Average Accuracy: 0.9188529253005981
BMA Accuracy: 0.9264000058174133
Accuracy Improvement: 0.0075470805168151855

ממוצע מודל בייסיאני מגדיל את הדיוק שלנו בכמעט 1%!

דוגמה: מערכת המלצות MovieLens

כעת ננסה לעשות מסקנות עם מערך ההמלצות של MovieLens, שהוא אוסף של משתמשים ודירוגיהם של סרטים שונים. באופן ספציפי, אנחנו יכולים לייצג MovieLens כקובץ \(N \times M\) מטריקס שעון \(W\) שבו \(N\) הוא מספר המשתמשים \(M\) הוא מספר סרטים; אנו מצפים \(N > M\). הערכים של \(W_{ij}\) הם בוליאני המציין אם לאו המשתמשים \(i\) צפו בסרט \(j\). שימו לב ש- MovieLens מספקת דירוגי משתמשים, אבל אנחנו מתעלמים מהם כדי לפשט את הבעיה.

ראשית, נטען את מערך הנתונים. נשתמש בגרסה עם מיליון דירוגים.

movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
          'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
          'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
          'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']

Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0...
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl…

HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value='')))
Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord
HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value='')))
Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.

נצטרך לעשות קצת עיבוד מקדים של בסיס הנתונים כדי לקבל את המטריצה שעון \(W\).

raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']

movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])

num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1

movie_titles = dict(zip(movielens['train']['movie_id'],
                        movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
                        genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
                     for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]

watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)

(6040, 3706)

אנו יכולים להגדיר במודל הגנרטיבי \(W\), באמצעות מודל פרוק מטריקס הסתברותית פשוטה. אנו מניחים סמויה \(N \times D\) מטריקס המשתמשים \(U\) וכן סמויה \(M \times D\) מטריקס הסרט \(V\), אשר בעת הכפלה לייצר את logits של ברנולי עבור המטריצה שעון \(W\). נצטרך גם כוללים וקטורים הטיה למשתמשים וסרטים, \(u\) ו \(v\).

\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]

זו מטריצה ​​די גדולה; 6040 משתמשים ו-3706 סרטים מובילים למטריצה ​​עם למעלה מ-22 מיליון ערכים בה. איך אנחנו ניגשים לריסוק המודל הזה? ובכן, אם אנו מניחים כי \(N > M\) (כלומר יש יותר משתמשים מאשר סרטים), אז זה יהיה הגיוני לפיצול המטריצה שעון פני ציר המשתמשים, כך שכל מכשיר יהיה נתח של מטריקס השעון המתאים רק חלק מהמשתמשים . בניגוד בדוגמה הקודמת, אולם, אנו גם אצטרך שבר את \(U\) מטריקס, שכן יש הטבעה עבור כל משתמש, כך שכל מכשיר יהיה אחראי שבר \(U\) וכן שבר של \(W\). מצד השני, \(V\) יהיה unsharded ולהיות מסתנכרן בין מכשירים.

sharded_watch_matrix = shard(watch_matrix)

לפני שאנו כותבים שלנו run , בואו נדבר על אתגרים נוספים במהירות עם sharding משתנה אקראי המקומי \(U\). בעת הפעלת HMC, וניל tfp.mcmc.HamiltonianMonteCarlo הקרנל יהיה לטעום התנע עבור כול רכיב של מדינת השרשרת. בעבר, רק משתנים אקראיים לא מפורקים היו חלק מהמצב הזה, והמומנטים היו זהים בכל מכשיר. כאשר יש לנו כעת sharded \(U\), אנחנו צריכים לדגום התנע שונה בכל מכשיר \(U\), בעודם דוגמים אותו התנע עבור \(V\). כדי להשיג זאת, אנו יכולים להשתמש tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo עם Sharded הפצת מומנטום. ככל שאנו ממשיכים לבצע חישוב מקביל ממדרגה ראשונה, אנו עשויים לפשט זאת, למשל על ידי נטילת מחוון רסיסה לגרעין HMC.

def make_run(*,
             axis_name,
             dim=20,
             num_chains=2,
             prior_variance=1.,
             step_size=1e-2,
             num_leapfrog_steps=100,
             num_burnin_steps=1000,
             num_results=500,
             ):
  @functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
  @jax.default_matmul_precision('tensorfloat32')
  def run(key, watch_matrix):
    num_users, num_movies = watch_matrix.shape

    Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)

    def prior_fn():
      user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
      user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
      movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
      movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
      return (user_embeddings, user_bias, movie_embeddings, movie_bias)
    prior = tfed.JointDistributionCoroutine(prior_fn)

    def model_fn():
      user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
      logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
                + user_bias[..., :, None] + movie_bias[..., None, :])
      yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
    model = tfed.JointDistributionCoroutine(model_fn)

    init_key, sample_key = random.split(key)
    initial_state = prior.sample(seed=init_key, sample_shape=num_chains)

    def target_log_prob(*state):
      return model.log_prob((*state, watch_matrix))

    momentum_distribution = tfed.JointDistributionSequential([
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
    ])

    # We pass in momentum_distribution here to ensure that the momenta for 
    # user_embeddings and user_bias are also sharded
    kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
                                                      num_leapfrog_steps,
                                                      momentum_distribution=momentum_distribution)

    num_adaptation_steps = int(0.8 * num_burnin_steps)
    kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)

    def trace_fn(state, pkr):
      return {
        'log_prob': target_log_prob(*state),
        'log_accept_ratio': pkr.inner_results.log_accept_ratio,
      }
    return tfm.sample_chain(
        num_results, initial_state,
        kernel=kernel,
        num_burnin_steps=num_burnin_steps,
        trace_fn=trace_fn,
        seed=sample_key)
  return run

אנחנו שוב נפעיל אותו פעם לאפסן את ההידור run .

%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 56 s, sys: 1min 24s, total: 2min 20s
Wall time: 3min 35s

כעת נריץ אותו שוב ללא תקורה של הקומפילציה.

%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s
Wall time: 3min 1s

נראה שהשלמנו כ-150,000 צעדי קפיצה בערך ב-3 דקות, אז בערך 83 צעדי קפיצה בשנייה! בואו נשרטט את יחס הקבלה וצפיפות היומן של הדגימות שלנו.

fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
  ax.plot(val[0]) # Indexing into a sharded array, each element is the same
  ax.set_title(key);

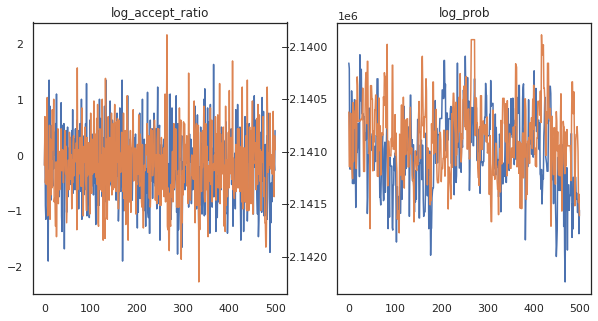
עכשיו, כשיש לנו כמה דוגמאות מרשת מרקוב שלנו, בואו נשתמש בהן כדי ליצור כמה תחזיות. ראשית, בואו נחלץ כל אחד מהרכיבים. זכור כי user_embeddings ו user_bias הם מפוצלים לרוחב המכשיר, כך שאנחנו צריכים לשרשר שלנו ShardedArray להשיג את כולם. מצד שני, movie_embeddings ו movie_bias זהים בכל מכשיר, אז אנחנו פשוט יכולים לבחור את הערך מתוך שבר הראשון. נשתמש רגיל numpy להעתיק את הערכים מהחלק האחורי TPUs כדי CPU.

user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')

User embeddings: (500, 2, 6040, 20)
User bias: (500, 2, 6040)
Movie embeddings: (500, 2, 3706, 20)
Movie bias: (500, 2, 3706)

בואו ננסה לבנות מערכת ממליצים פשוטה המנצלת את אי הוודאות שנלכדה בדגימות אלו. קודם כל נכתוב פונקציה שמדרגת סרטים לפי הסתברות הצפייה.

@jax.jit
def recommend(sample, user_id):
  user_embeddings, user_bias, movie_embeddings, movie_bias = sample
  movie_logits = (
      jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
      + user_bias[user_id] + movie_bias)
  return movie_logits.argsort()[::-1]

כעת אנו יכולים לכתוב פונקציה שעוברת לולאה על כל הדגימות ולכל אחת מהן, בוחרת את הסרט בדירוג העליון שהמשתמש לא צפה בו. לאחר מכן נוכל לראות את הספירות של כל הסרטים המומלצים על פני הדוגמאות.

def get_recommendations(user_id): 
  movie_ids = []
  already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
  for i in range(500):
    for j in range(2):
      sample = jax.tree_map(lambda x: x[i, j], samples)
      ranking = recommend(sample, user_id)
      for movie_id in ranking:
        if int(movie_id) not in already_watched:
          movie_ids.append(movie_id)
          break
  return movie_ids

def plot_recommendations(movie_ids, ax=None):
  titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
  ax = ax or plt.gca()
  names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
  ax.bar(names, counts)
  ax.set_xticklabels(names, rotation=90)

בואו ניקח את המשתמש שראה הכי הרבה סרטים מול זה שראה הכי פחות.

user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])

2314 20

אנו מקווים במערכת שלנו יש יותר ודאות לגבי user_most מ user_least , בהתחשב בכך שיש לנו מידע נוסף על מה מיני סרטים user_most סביר יותר לצפות.

fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');

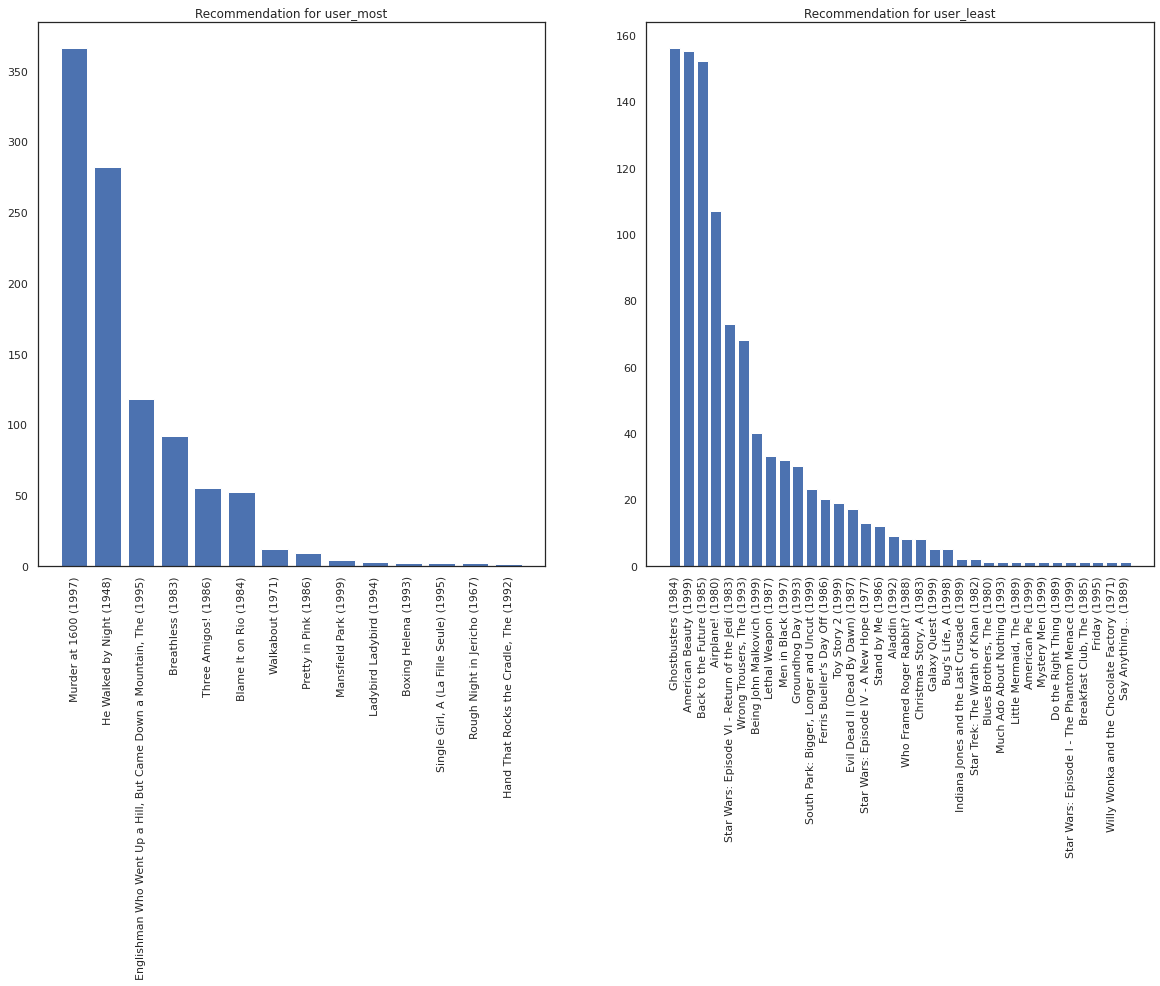
אנחנו רואים שיש יותר משונות המלצותינו user_least משקף הוודאות הנוספת שלנו העדפות הצפייה שלהם.

אנחנו יכולים גם לראות להסתכל על הז'אנרים של הסרטים המומלצים.

most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');

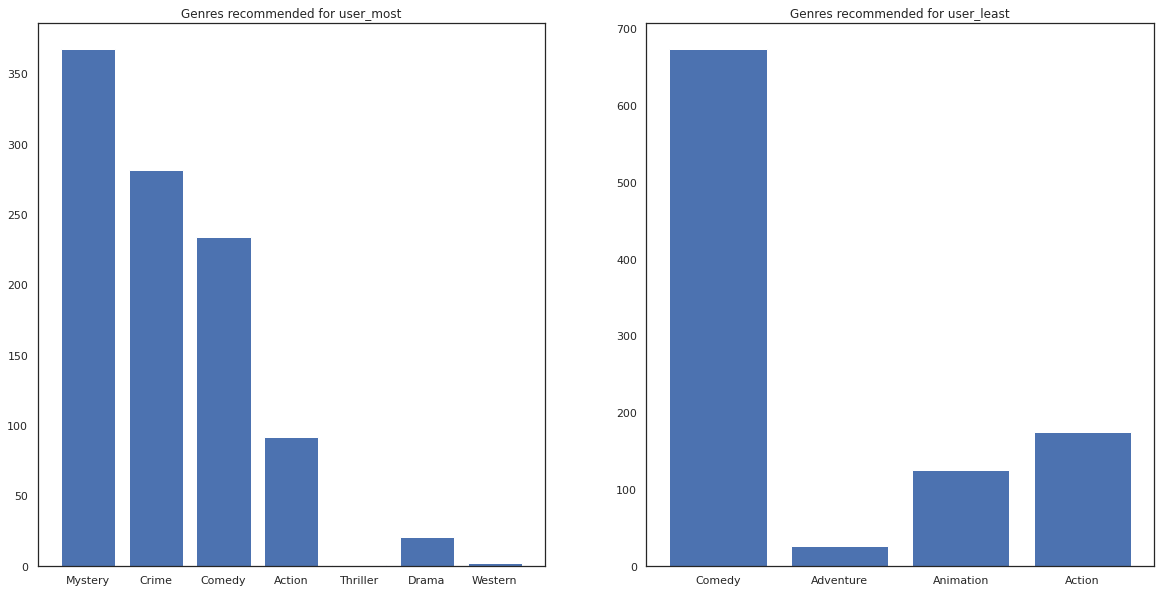
user_most ראה הרבה סרטים והומלץ ז'אנרי נישה יותר כמו מסתורין פשע בעוד user_least לא צפה בסרטים רבים הומלץ יותר סרטים המיינסטרים, אשר קומדיה ופעולה מלוכסנות.