Voir sur TensorFlow.org

Exécuter dans Google Colab

Voir la source sur GitHub

Télécharger le cahier

TensorFlow Probability (TFP) sur JAX dispose désormais d'outils pour le calcul numérique distribué. Pour s'adapter à un grand nombre d'accélérateurs, les outils sont construits autour de l'écriture de code à l'aide du paradigme « programme unique à données multiples », ou SPMD en abrégé.

Dans ce cahier, nous verrons comment « penser en SPMD » et présenterons les nouvelles abstractions TFP pour la mise à l'échelle vers des configurations telles que des pods TPU ou des clusters de GPU. Si vous exécutez ce code vous-même, assurez-vous de sélectionner un environnement d'exécution TPU.

Nous allons d'abord installer les dernières versions TFP, JAX et TF.

Installe

pip install jaxlib --upgrade -q 2>&1 1> /dev/null
pip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/null
pip install tf-nightly-cpu -q -I 2>&1 1> /dev/null
pip install jax -I -q --upgrade 2>&1 1>/dev/null

Nous importerons quelques bibliothèques générales, ainsi que quelques utilitaires JAX.

Configuration et importations

import functools
import collections
import contextlib

import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds

from tensorflow_probability.substrates import jax as tfp

sns.set(style='white')

INFO:tensorflow:Enabling eager execution
INFO:tensorflow:Enabling v2 tensorshape
INFO:tensorflow:Enabling resource variables
INFO:tensorflow:Enabling tensor equality
INFO:tensorflow:Enabling control flow v2

Nous allons également mettre en place des alias TFP pratiques. Les nouvelles abstractions sont actuellement fournis dans tfp.experimental.distribute et tfp.experimental.mcmc .

tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc

Root = tfed.JointDistributionCoroutine.Root

Pour connecter le notebook à un TPU, nous utilisons l'assistant suivant de JAX. Pour confirmer que nous sommes connectés, nous imprimons le nombre d'appareils, qui devrait être huit.

from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')

Found 8 devices

Une introduction rapide à jax.pmap

Après la connexion à un TPU, nous avons accès à huit appareils. Cependant, lorsque nous exécutons du code JAX avec impatience, JAX par défaut n'exécute les calculs que sur un seul.

Le moyen le plus simple d'exécuter un calcul sur de nombreux appareils consiste à mapper une fonction, chaque appareil exécutant un index de la carte. JAX fournit le jax.pmap ( « plan parallèle ») transformation qui transforme une fonction en une fonction qui mappe le couvre plusieurs dispositifs.

Dans l'exemple suivant, nous créons un tableau de taille 8 (pour correspondre au nombre d'appareils disponibles) et mappons une fonction qui en ajoute 5.

xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)

<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5.  6.  7.  8.  9. 10. 11. 12.]

Notez que nous recevons un ShardedDeviceArray arrière de type, ce qui indique que le tableau de sortie est divisé physiquement sur tous les appareils.

jax.pmap agit sémantiquement comme une carte, mais a quelques options importantes qui modifient son comportement. Par défaut, pmap assume toutes les entrées de la fonction sont mis en correspondance sur, mais nous pouvons modifier ce comportement avec le in_axes argument.

xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)

[ 5.  6.  7.  8.  9. 10. 11. 12.]

De manière analogue, le out_axes argument pmap détermine si oui ou non pour retourner les valeurs sur chaque appareil. Réglage out_axes à None renvoie automatiquement la valeur sur le 1er appareil et ne doivent être utilisés si nous sommes convaincus que les valeurs sont les mêmes sur tous les appareils.

xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)

2.0

Que se passe-t-il lorsque ce que nous aimerions faire n'est pas facilement exprimable en tant que fonction pure mappée ? Par exemple, que se passe-t-il si nous souhaitons faire une somme sur l'axe sur lequel nous cartographions ? JAX propose des "collectifs", des fonctions qui communiquent entre les appareils, pour permettre l'écriture de programmes distribués plus intéressants et complexes. Pour comprendre exactement comment ils fonctionnent, nous allons présenter SPMD.

Qu'est-ce que le SPMD ?

Un seul programme multi-données (SPMD) est un modèle de programmation simultanée dans lequel un seul programme (c'est-à-dire le même code) est exécuté simultanément sur tous les appareils, mais les entrées de chacun des programmes en cours d'exécution peuvent différer.

Si notre programme est une simple fonction de ses entrées ( par exemple quelque chose comme x + 5 ), l' exécution d' un programme DGBS est la cartographie juste des données sur différentes, comme nous l' avons fait avec jax.pmap plus tôt. Cependant, nous pouvons faire plus que simplement « mapper » une fonction. JAX propose des « collectifs », qui sont des fonctions qui communiquent entre les appareils.

Par exemple, nous aimerions peut-être prendre la somme d'une quantité sur tous nos appareils. Avant de le faire, nous devons attribuer un nom au nous sur la cartographie Axe dans êtes la la pmap . Nous utilisons ensuite la lax.psum fonction ( « somme parallèle ») pour effectuer une somme sur tous les appareils, nous assurer que nous identifions le nous somme nommé axe sur.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)

ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)

Le psum agrégats collectifs , la valeur de x sur chaque dispositif et synchronise sa valeur à travers la carte -à- dire out est 28. de chaque dispositif. Nous n'effectuons plus une simple « carte », mais nous exécutons un programme SPMD où le calcul de chaque appareil peut désormais interagir avec le même calcul sur d'autres appareils, bien que de manière limitée en utilisant des collectifs. Dans ce scénario, nous pouvons utiliser out_axes = None , car psum synchronise la valeur.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))

ShardedDeviceArray(28., dtype=float32)

SPMD nous permet d'écrire un programme qui s'exécute sur chaque appareil dans n'importe quelle configuration TPU simultanément. Le même code qui est utilisé pour faire de l'apprentissage automatique sur 8 cœurs TPU peut être utilisé sur un pod TPU qui peut avoir des centaines à des milliers de cœurs ! Pour un tutoriel plus détaillées sur jax.pmap et DGBS, vous pouvez vous référer au le tutoriel JAX 101 .

MCMC à grande échelle

Dans ce cahier, nous nous concentrons sur l'utilisation des méthodes de Markov Chain Monte Carlo (MCMC) pour l'inférence bayésienne. Il existe plusieurs façons d'utiliser de nombreux périphériques pour MCMC, mais dans ce cahier, nous nous concentrerons sur deux :

1. Exécution de chaînes de Markov indépendantes sur différents appareils. Ce cas est assez simple et est réalisable avec la TFP vanille.
2. Partage d'un ensemble de données sur plusieurs appareils. Ce cas est un peu plus complexe et nécessite des machines TFP récemment ajoutées.

Chaînes indépendantes

Disons que nous aimerions faire une inférence bayésienne sur un problème à l'aide de MCMC et que nous aimerions exécuter plusieurs chaînes en parallèle sur plusieurs appareils (disons 2 sur chaque appareil). Cela s'avère être un programme que nous pouvons simplement « mapper » sur plusieurs appareils, c'est-à-dire un programme qui n'a pas besoin de collectifs. Pour nous assurer que chaque programme exécute une chaîne de Markov différente (au lieu d'exécuter la même), nous passons une valeur différente pour la graine aléatoire à chaque périphérique.

Essayons-le sur un problème jouet d'échantillonnage à partir d'une distribution gaussienne 2D. Nous pouvons utiliser la fonctionnalité MCMC existante de TFP prête à l'emploi. En général, nous essayons de mettre la majeure partie de la logique à l'intérieur de notre fonction mappée pour distinguer plus explicitement ce qui s'exécute sur tous les appareils par rapport au premier.

def run(seed):
  target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob

  initial_state = jnp.zeros([2, 2]) # 2 chains
  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
  def trace_fn(state, pkr):
    return target_log_prob(state)

  states, log_prob = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    kernel=kernel,
    current_state=initial_state,
    trace_fn=trace_fn,
    seed=seed
  )
  return states, log_prob

En soi, la run fonction prend dans une graine aléatoire sans état (pour voir comment le travail de caractère aléatoire sans état, vous pouvez lire le TFP sur JAX ordinateur portable ou voir le tutoriel JAX 101 ). Cartographie run sur différentes semences entraînera l' exécution de plusieurs chaînes de Markov indépendantes.

states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)

(8, 1000, 2, 2) (8, 1000, 2)

Notez comment nous avons maintenant un axe supplémentaire correspondant à chaque appareil. On peut réarranger les dimensions et les aplatir pour obtenir un axe pour les 16 chaînes.

states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])

fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()

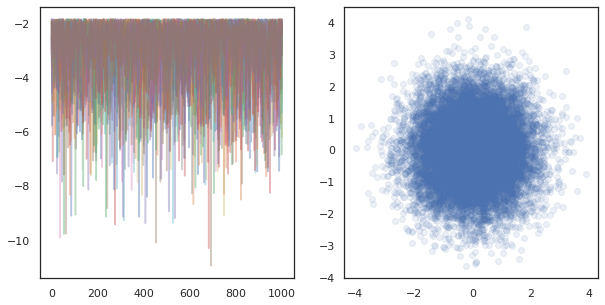
Lors de l' exécution des chaînes indépendantes sur de nombreux appareils, il est aussi facile que pmap -ment sur une fonction qui utilise tfp.mcmc , assurant que nous passer des valeurs différentes pour la semence aléatoire à chaque appareil.

Partage des données

Lorsque nous faisons MCMC, la distribution cible est souvent une distribution postérieure obtenue en conditionnant sur un ensemble de données, et le calcul d'une densité logarithmique non normalisée implique la somme des vraisemblances pour chaque donnée observée.

Avec des ensembles de données très volumineux, il peut être prohibitif même d'exécuter une chaîne sur un seul appareil. Cependant, lorsque nous avons accès à plusieurs appareils, nous pouvons répartir l'ensemble de données entre les appareils pour mieux exploiter le calcul dont nous disposons.

Si nous aimerions faire MCCM avec un ensemble de données fragmentées, nous devons assurer le journal densité non normalisée on calcule sur chaque appareil représente le total, soit la densité sur toutes les données, sinon chaque appareil va faire MCCM avec leur propre cible incorrecte Distribution. À cette fin, TFP a maintenant de nouveaux outils (c. -à- tfp.experimental.distribute et tfp.experimental.mcmc ) qui permettent de calcul « probabilités » de fragmentées journal et de faire MCCM avec eux.

Distributions fragmentées

L'abstraction noyau PTF prévoit maintenant le calcul probabiliities log fragmentées est le Sharded méta-distribution, qui prend une distribution en entrée et renvoie une nouvelle distribution qui a des propriétés spécifiques lorsqu'elles sont exécutées dans un contexte de SPMD. Sharded vit à tfp.experimental.distribute .

Intuitivement, un Sharded correspond de distribution à un ensemble de variables aléatoires qui ont été « split » sur tous les appareils. Sur chaque appareil, ils produiront des échantillons différents et peuvent avoir individuellement des densités logarithmiques différentes. En variante, un Sharded correspond de distribution à un « plateau » dans le langage de modélisation graphique, où la taille de la plaque est le nombre de dispositifs.

L' échantillonnage d' un Sharded de distribution

Si nous échantillon d'une Normal de distribution dans un être du programme pmap -El en utilisant la même graine sur chaque appareil, nous aurons le même échantillon sur chaque appareil. Nous pouvons considérer la fonction suivante comme échantillonnant une seule variable aléatoire qui est synchronisée sur tous les appareils.

# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
  return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                    -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32)

Si nous emballons tfd.Normal(0., 1.) avec un tfed.Sharded , nous avons logiquement maintenant huit différentes variables aléatoires (un sur chaque appareil) et produira donc un échantillon différent pour chacun, malgré le passage dans la même graine .

def f(seed, _):
  return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([ 1.2152631 ,  0.7818249 ,  0.32549605,  0.6828047 ,
                     1.3973192 , -0.57830244,  0.37862757,  2.7706041 ],                   dtype=float32)

Une représentation équivalente de cette distribution sur un seul appareil est juste 8 échantillons normaux indépendants. Même si la valeur de l'échantillon sera différent ( tfed.Sharded que la génération de nombres pseudo-aléatoires légèrement différente), ils représentent tous deux la même distribution.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))

DeviceArray([ 0.08086783, -0.38624594, -0.3756545 ,  1.668957  ,
             -1.2758069 ,  2.1192007 , -0.85821325,  1.1305912 ],            dtype=float32)

En prenant le log-densité d'une Sharded de distribution

Voyons ce qui se passe lorsque nous calculons la densité logarithmique d'un échantillon à partir d'une distribution régulière dans un contexte SPMD.

def f(seed, _):
  dist = tfd.Normal(0., 1.)
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                     -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32),
 ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
                     -0.94012403, -0.94012403, -0.94012403, -0.94012403],                   dtype=float32))

Chaque échantillon est le même sur chaque appareil, nous calculons donc la même densité sur chaque appareil également. Intuitivement, nous n'avons ici qu'une distribution sur une seule variable normalement distribuée.

Avec une Sharded distribution, nous avons une distribution de plus de 8 variables aléatoires, donc quand on calcule la log_prob d'un échantillon, on somme, à travers les dispositifs, sur chacune des densités individuelles de log. (Vous remarquerez peut-être que cette valeur totale de log_prob est supérieure au singleton log_prob calculé ci-dessus.)

def f(seed, _):
  dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
    random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)

Sample: [ 1.2152631   0.7818249   0.32549605  0.6828047   1.3973192  -0.57830244
  0.37862757  2.7706041 ]
Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205
 -13.7349205 -13.7349205]

La distribution équivalente, "unsharded" produit la même densité de log.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)

DeviceArray(-13.7349205, dtype=float32)

Une Sharded de distribution produit des valeurs différentes de l' sample sur chaque appareil, mais obtenir la même valeur pour log_prob sur chaque appareil. Qu'est-ce qu'il se passe ici? Un Sharded de distribution fait un psum interne pour assurer les log_prob valeurs sont synchronisés à travers les dispositifs. Pourquoi voudrions-nous ce comportement ? Si nous courons la même chaîne MCMC sur chaque appareil, nous aimerions que le target_log_prob être le même sur chaque appareil, même si certaines variables aléatoires dans le calcul sont fragmentées à travers les dispositifs.

En outre, un Sharded assure que les gradients de distribution à travers les dispositifs sont correct, pour garantir que les algorithmes comme HMC, qui prennent des gradients de la fonction log-densité dans le cadre de la fonction de transition, donnent des échantillons appropriés.

Fragmentées JointDistribution s

Nous pouvons créer des modèles avec plusieurs Sharded variables aléatoires à l'aide JointDistribution s (JDs). Malheureusement, Sharded distributions ne peuvent pas être utilisés en toute sécurité à la vanille tfd.JointDistribution s, mais tfp.experimental.distribute exportations « patchés » JDS se comportera comme Sharded distributions.

def f(seed, _):
  dist = tfed.JointDistributionSequential([
    tfd.Normal(0., 1.),
    tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
  ])
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
                      1.6121525, 1.6121525, 1.6121525], dtype=float32),
  ShardedDeviceArray([ 0.8690128 , -0.83167845,  1.2209264 ,  0.88412696,
                       0.76478404, -0.66208494, -0.0129658 ,  0.7391483 ],                   dtype=float32)],
 ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
                     -12.214451, -12.214451, -12.214451, -12.214451],                   dtype=float32))

Ces JDs peuvent avoir des fragmentées Sharded distributions et TFP vanille en tant que composants. Pour les distributions non partitionnées, nous obtenons le même échantillon sur chaque périphérique, et pour les distributions partitionnées, nous obtenons des échantillons différents. Le log_prob sur chaque périphérique est synchronisée aussi bien.

MCMC avec Sharded distributions

Comment pouvons-nous penser à Sharded distributions dans le cadre de MCCM? Si nous avons un modèle génératif qui peut être exprimé en JointDistribution , on peut choisir un certain axe de ce modèle à « tesson » à travers. En règle générale, une variable aléatoire dans le modèle correspondra aux données observées, et si nous avons un grand ensemble de données que nous aimerions fragmenter sur plusieurs appareils, nous voulons que les variables associées aux points de données soient également fragmentées. Nous pouvons également avoir des variables aléatoires "locales" qui sont un à un avec les observations que nous partitionnons, nous devrons donc partitionner en plus ces variables aléatoires.

Nous allons passer en revue les exemples de l'utilisation des Sharded distributions avec TFP MCCM dans cette section. Nous allons commencer par un exemple de régression logistique bayésienne plus simple, et conclure par un exemple de matrice factorisation, dans le but de démontrer certains cas d' utilisation pour la distribute bibliothèque.

Exemple : régression logistique bayésienne pour MNIST

Nous aimerions faire une régression logistique bayésienne sur un grand ensemble de données ; le modèle a un avant \(p(\theta)\) sur les coefficients de régression, et une probabilité \(p(y_i | \theta, x_i)\) qui est additionnée sur toutes les données \(\{x_i, y_i\}_{i = 1}^N\) pour obtenir la densité totale du journal commun. Si nous Shard nos données, nous avions Shard les variables aléatoires observées \(x_i\) et \(y_i\) dans notre modèle.

Nous utilisons le modèle de régression logistique bayésienne suivant pour la classification MNIST :

\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]

Chargeons MNIST à l'aide des ensembles de données TensorFlow.

mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.

raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.

Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1...
WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your
local data directory. If you'd instead prefer to read directly from our public
GCS bucket (recommended if you're running on GCP), you can instead pass
`try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`.
HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio…
Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.

Nous avons 60000 images d'entraînement mais profitons de nos 8 cœurs disponibles et divisons-les de 8 manières. Nous allons utiliser cette pratique shard fonction d'utilité.

def shard_value(x):
  x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
  return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices

shard = functools.partial(jax.tree_map, shard_value)

sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)

(8, 7500, 784) (8, 7500)

Avant de continuer, discutons rapidement de la précision sur les TPU et de son impact sur la console HMC. PUT exécuter multiplications de matrice à l' aide de faible bfloat16 précision pour la vitesse. bfloat16 matrice multiplications sont souvent suffisantes pour de nombreuses applications d'apprentissage en profondeur, mais lorsqu'il est utilisé avec la console HMC, nous avons empiriquement la précision inférieure peut conduire à des trajectoires divergentes, ce qui provoque des rejets. Nous pouvons utiliser des multiplications matricielles plus précises, au prix de quelques calculs supplémentaires.

Pour augmenter notre précision matmul, nous pouvons utiliser le jax.default_matmul_precision décorateur avec "tensorfloat32" précision (pour une précision encore plus que nous pourrions utiliser "float32" précision).

Définissons maintenant notre run fonction, qui prendra dans une graine aléatoire (qui sera le même sur chaque appareil) et un tesson de MNIST. La fonction implémentera le modèle susmentionné et nous utiliserons ensuite la fonctionnalité MCMC vanille de TFP pour exécuter une seule chaîne. Nous nous assurerons de décorant les run avec le jax.default_matmul_precision décorateur pour vous assurer que la multiplication de la matrice est exécutée avec une plus grande précision, bien que dans l'exemple ci - dessous en particulier, nous pourrions tout aussi bien utiliser jnp.dot(images, w, precision=lax.Precision.HIGH) .

# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device. 
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
  images, labels = data # a sharded dataset
  num_examples, dim = images.shape
  num_classes = 10

  def model_fn():
    w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
    b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
    logits = jnp.dot(images, w) + b
    yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
                       shard_axis_name='data')
  model = tfed.JointDistributionCoroutine(model_fn)

  init_seed, sample_seed = random.split(seed)

  initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`

  def target_log_prob(*state):
    return model.log_prob((*state, labels))

  def accuracy(w, b):
    logits = images.dot(w) + b
    preds = logits.argmax(axis=-1)
    # We take the average accuracy across devices by using `lax.pmean`
    return lax.pmean((preds == labels).mean(), 'data')

  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
  kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
  def trace_fn(state, pkr):
    return (
        target_log_prob(*state),
        accuracy(*state),
        pkr.new_step_size)
  states, trace = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    current_state=initial_state,
    kernel=kernel,
    trace_fn=trace_fn,
    seed=sample_seed
  )
  return states, trace

jax.pmap comprend une compilation JIT mais la fonction compilé est mis en cache après le premier appel. Nous appellerons run et d' ignorer la sortie pour mettre en cache la compilation.

%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s
Wall time: 1min 54s

Nous allons maintenant entendre run à nouveau pour voir combien de temps l'exécution réelle prend.

%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s
Wall time: 1min 43s

Nous exécutons 200 000 étapes de sauts-de-mouton, dont chacune calcule un gradient sur l'ensemble de données. Répartir le calcul sur 8 cœurs nous permet de calculer l'équivalent de 200 000 époques d'entraînement en environ 95 secondes, soit environ 2 100 époques par seconde !

Traçons la densité logarithmique de chaque échantillon et la précision de chaque échantillon :

fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()

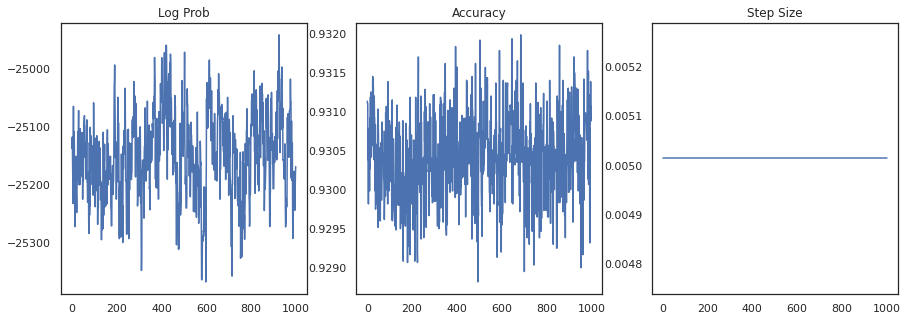
Si nous regroupons les échantillons, nous pouvons calculer une moyenne du modèle bayésien pour améliorer nos performances.

@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
  images, labels = data
  logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
  probs = jax.nn.softmax(logits, axis=-1)
  bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
  avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
  return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')

sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')

Average Accuracy: 0.9188529253005981
BMA Accuracy: 0.9264000058174133
Accuracy Improvement: 0.0075470805168151855

Une moyenne de modèle bayésien augmente notre précision de près de 1 % !

Exemple : système de recommandation MovieLens

Essayons maintenant de faire une inférence avec l'ensemble de données de recommandations MovieLens, qui est une collection d'utilisateurs et de leurs notes sur divers films. Plus précisément, nous pouvons représenter MovieLens comme un \(N \times M\) matrice montre \(W\) où \(N\) est le nombre d'utilisateurs et \(M\) est le nombre de films; nous nous attendons à \(N > M\). Les entrées de \(W_{ij}\) sont un booléen indiquant si oui ou non l' utilisateur \(i\) film regardé \(j\). Notez que MovieLens fournit des évaluations d'utilisateurs, mais nous les ignorons pour simplifier le problème.

Tout d'abord, nous allons charger l'ensemble de données. Nous utiliserons la version avec 1 million de notes.

movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
          'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
          'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
          'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']

Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0...
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl…

HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value='')))
Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord
HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value='')))
Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.

Nous ferons une pré - traitement de l'ensemble de données pour obtenir la matrice de montre \(W\).

raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']

movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])

num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1

movie_titles = dict(zip(movielens['train']['movie_id'],
                        movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
                        genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
                     for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]

watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)

(6040, 3706)

Nous pouvons définir un modèle génératif pour \(W\), en utilisant un modèle de matrice de factorisation probabiliste simple. Nous supposons une latente \(N \times D\) matrice utilisateur \(U\) et latente \(M \times D\) matrice de film \(V\)qui Multiplié produisent logits d'une Bernoulli pour la matrice de montre \(W\). Nous allons inclure aussi un des vecteurs de biais pour les utilisateurs et les films, \(u\) et \(v\).

\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]

C'est une assez grosse matrice ; 6040 utilisateurs et 3706 films mènent à une matrice contenant plus de 22 millions d'entrées. Comment abordons-nous le sharding de ce modèle ? Eh bien, si nous supposons que \(N > M\) (autrement dit , il y a plus d' utilisateurs que des films), il serait alors logique de shard la matrice montre à travers l'axe de l' utilisateur, de sorte que chaque dispositif aurait une partie de la matrice de montre correspondant à un sous - ensemble d'utilisateurs . Contrairement à l'exemple précédent, cependant, nous allons aussi Shard la \(U\) matrice, car il a un plongement pour chaque utilisateur, de sorte que chaque appareil sera responsable d'un tesson de \(U\) et un tesson de \(W\). D'autre part, \(V\) sera unsharded et être synchronisé sur tous les appareils.

sharded_watch_matrix = shard(watch_matrix)

Avant d' écrire notre run , nous allons discuter rapidement des défis supplémentaires avec sharding local variable aléatoire \(U\). Lors de l' exécution HMC, la vanille tfp.mcmc.HamiltonianMonteCarlo noyau échantillon pour chaque élément impulsions de l'état de la chaîne. Auparavant, seules les variables aléatoires non partagées faisaient partie de cet état et les impulsions étaient les mêmes sur chaque appareil. Quand nous avons maintenant un fragmentées \(U\), nous avons besoin de goûter à différentes moments sur chaque appareil pour \(U\), tout en goûtant le même pour impulsions \(V\). Pour ce faire , nous pouvons utiliser tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo avec une Sharded distribution dynamique. Comme nous continuons à faire du calcul parallèle de première classe, nous pouvons simplifier cela, par exemple en prenant un indicateur de shardedness au noyau HMC.

def make_run(*,
             axis_name,
             dim=20,
             num_chains=2,
             prior_variance=1.,
             step_size=1e-2,
             num_leapfrog_steps=100,
             num_burnin_steps=1000,
             num_results=500,
             ):
  @functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
  @jax.default_matmul_precision('tensorfloat32')
  def run(key, watch_matrix):
    num_users, num_movies = watch_matrix.shape

    Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)

    def prior_fn():
      user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
      user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
      movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
      movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
      return (user_embeddings, user_bias, movie_embeddings, movie_bias)
    prior = tfed.JointDistributionCoroutine(prior_fn)

    def model_fn():
      user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
      logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
                + user_bias[..., :, None] + movie_bias[..., None, :])
      yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
    model = tfed.JointDistributionCoroutine(model_fn)

    init_key, sample_key = random.split(key)
    initial_state = prior.sample(seed=init_key, sample_shape=num_chains)

    def target_log_prob(*state):
      return model.log_prob((*state, watch_matrix))

    momentum_distribution = tfed.JointDistributionSequential([
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
    ])

    # We pass in momentum_distribution here to ensure that the momenta for 
    # user_embeddings and user_bias are also sharded
    kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
                                                      num_leapfrog_steps,
                                                      momentum_distribution=momentum_distribution)

    num_adaptation_steps = int(0.8 * num_burnin_steps)
    kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)

    def trace_fn(state, pkr):
      return {
        'log_prob': target_log_prob(*state),
        'log_accept_ratio': pkr.inner_results.log_accept_ratio,
      }
    return tfm.sample_chain(
        num_results, initial_state,
        kernel=kernel,
        num_burnin_steps=num_burnin_steps,
        trace_fn=trace_fn,
        seed=sample_key)
  return run

Nous nous représenterons une fois pour mettre en cache la compilation run .

%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 56 s, sys: 1min 24s, total: 2min 20s
Wall time: 3min 35s

Nous allons maintenant l'exécuter à nouveau sans la surcharge de compilation.

%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s
Wall time: 3min 1s

On dirait que nous avons effectué environ 150 000 pas de saute-mouton en 3 minutes environ, donc environ 83 pas de saute-mouton par seconde ! Traçons le taux d'acceptation et la densité logarithmique de nos échantillons.

fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
  ax.plot(val[0]) # Indexing into a sharded array, each element is the same
  ax.set_title(key);

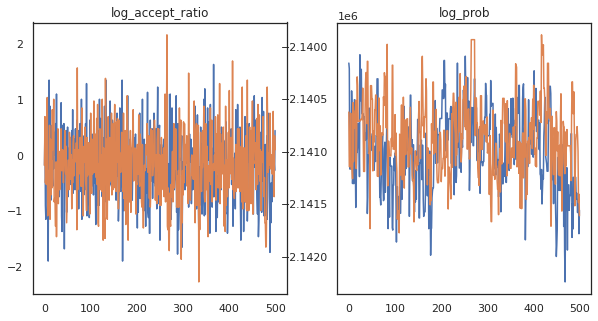
Maintenant que nous avons quelques échantillons de notre chaîne de Markov, utilisons-les pour faire des prédictions. Tout d'abord, extrayons chacun des composants. Rappelez - vous que les user_embeddings et user_bias sont répartis à travers l' appareil, donc nous devons concaténer notre ShardedArray pour les obtenir tous. D'autre part, movie_embeddings et movie_bias sont les mêmes sur tous les appareils, afin que nous puissions simplement choisir la valeur de la première tesson. Nous allons utiliser régulièrement numpy pour copier les valeurs de l'arrière de PUT à la CPU.

user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')

User embeddings: (500, 2, 6040, 20)
User bias: (500, 2, 6040)
Movie embeddings: (500, 2, 3706, 20)
Movie bias: (500, 2, 3706)

Essayons de construire un système de recommandation simple qui utilise l'incertitude capturée dans ces échantillons. Écrivons d'abord une fonction qui classe les films en fonction de la probabilité de visionnage.

@jax.jit
def recommend(sample, user_id):
  user_embeddings, user_bias, movie_embeddings, movie_bias = sample
  movie_logits = (
      jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
      + user_bias[user_id] + movie_bias)
  return movie_logits.argsort()[::-1]

Nous pouvons maintenant écrire une fonction qui parcourt tous les échantillons et pour chacun, sélectionne le film le mieux classé que l'utilisateur n'a pas encore regardé. Nous pouvons alors voir le nombre de tous les films recommandés dans les échantillons.

def get_recommendations(user_id): 
  movie_ids = []
  already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
  for i in range(500):
    for j in range(2):
      sample = jax.tree_map(lambda x: x[i, j], samples)
      ranking = recommend(sample, user_id)
      for movie_id in ranking:
        if int(movie_id) not in already_watched:
          movie_ids.append(movie_id)
          break
  return movie_ids

def plot_recommendations(movie_ids, ax=None):
  titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
  ax = ax or plt.gca()
  names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
  ax.bar(names, counts)
  ax.set_xticklabels(names, rotation=90)

Prenons l'utilisateur qui a vu le plus de films par rapport à celui qui en a vu le moins.

user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])

2314 20

Nous espérons que notre système a plus de certitude au sujet user_most que user_least , étant donné que nous avons plus d' informations sur ce genre de films user_most est plus susceptible de regarder.

fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');

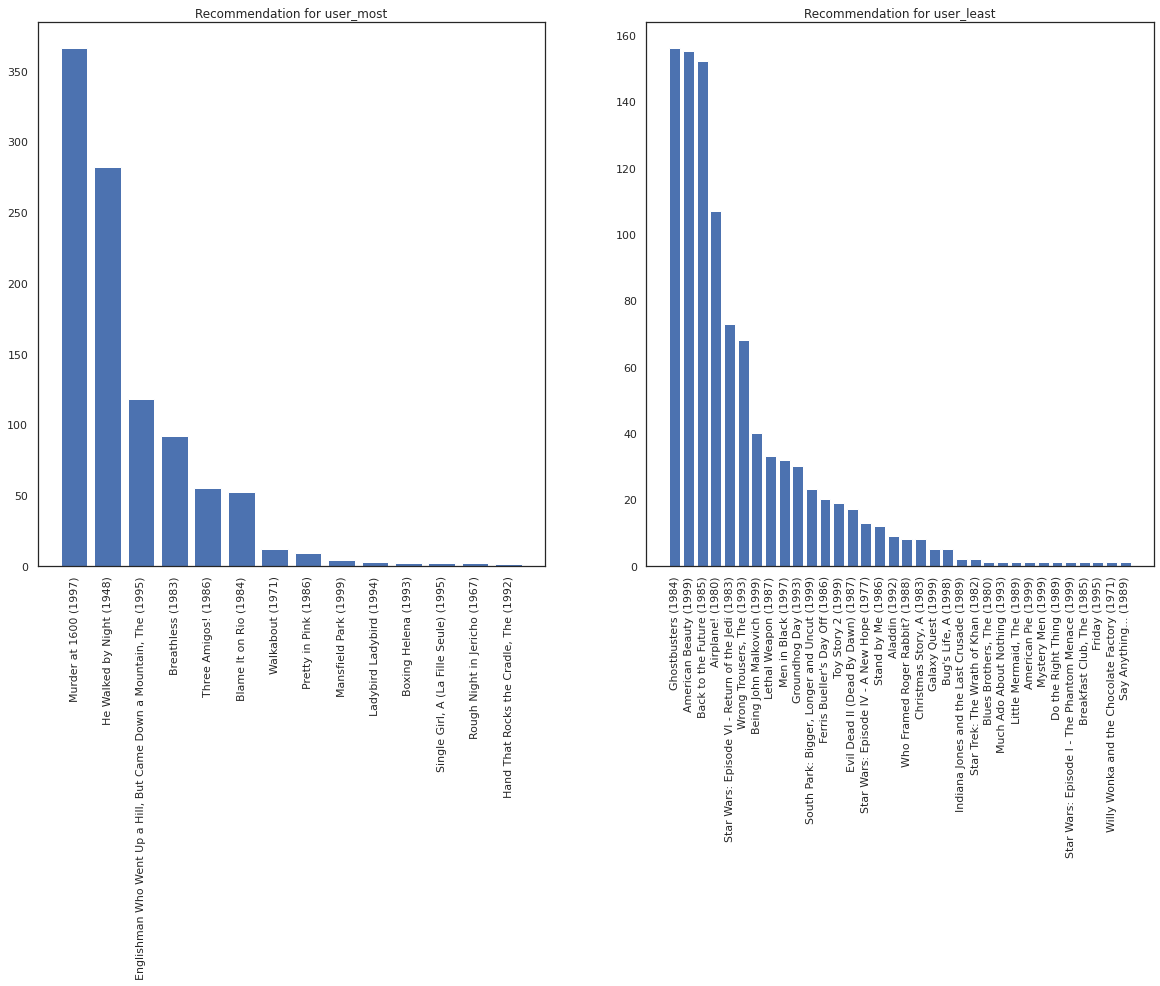
Nous voyons qu'il ya plus de variance dans nos recommandations pour user_least qui reflète notre incertitude supplémentaire dans leurs préférences de la montre.

Nous pouvons également voir regarder les genres des films recommandés.

most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');

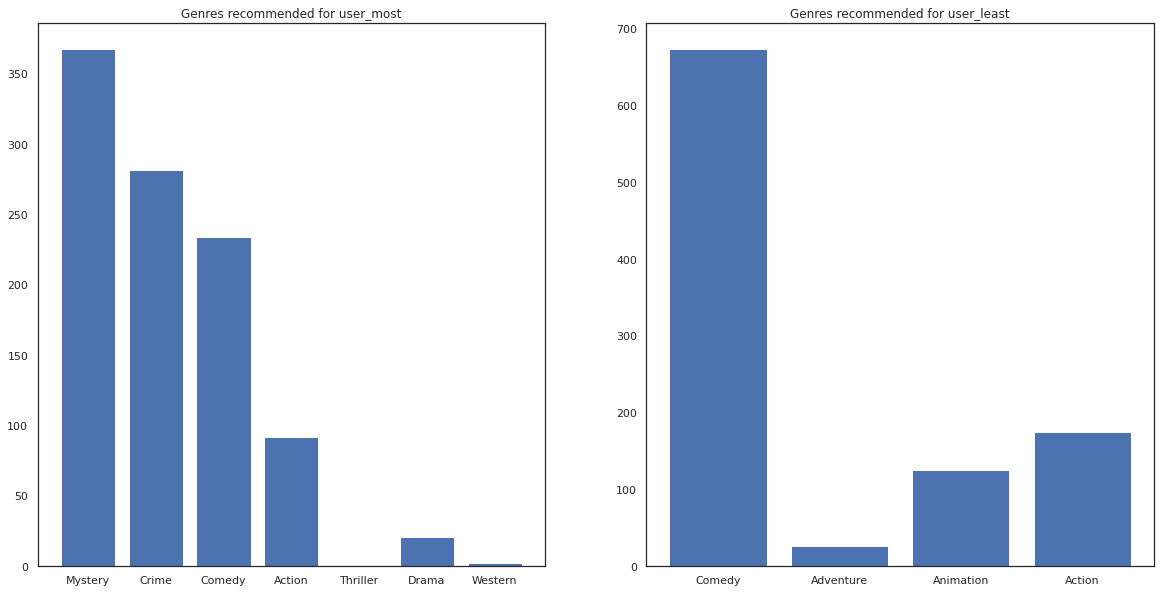
user_most a vu beaucoup de films et a été plus genres de niche comme recommandé mystère et de la criminalité alors que user_least n'a pas regardé de nombreux films et a été recommandé plus de films traditionnels, qui comédie obliquité et de l' action.