مشاهده در TensorFlow.org

در Google Colab اجرا شود

مشاهده منبع در GitHub

دانلود دفترچه یادداشت

TensorFlow Probability (TFP) در JAX اکنون ابزارهایی برای محاسبات عددی توزیع شده دارد. برای مقیاس‌بندی به تعداد زیادی شتاب‌دهنده، ابزارها حول نوشتن کد با استفاده از پارادایم «تک برنامه‌ای چندگانه» یا به اختصار SPMD ساخته شده‌اند.

در این نوت بوک، به نحوه "فکر کردن در SPMD" و معرفی انتزاعات TFP جدید برای مقیاس بندی به پیکربندی هایی مانند TPU pods یا خوشه های GPU خواهیم پرداخت. اگر خودتان این کد را اجرا می کنید، مطمئن شوید که زمان اجرای TPU را انتخاب کنید.

ابتدا آخرین نسخه‌های TFP، JAX و TF را نصب می‌کنیم.

نصب می کند

pip install jaxlib --upgrade -q 2>&1 1> /dev/null
pip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/null
pip install tf-nightly-cpu -q -I 2>&1 1> /dev/null
pip install jax -I -q --upgrade 2>&1 1>/dev/null

ما تعدادی کتابخانه عمومی را به همراه برخی از ابزارهای JAX وارد خواهیم کرد.

راه اندازی و واردات

import functools
import collections
import contextlib

import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds

from tensorflow_probability.substrates import jax as tfp

sns.set(style='white')

INFO:tensorflow:Enabling eager execution
INFO:tensorflow:Enabling v2 tensorshape
INFO:tensorflow:Enabling resource variables
INFO:tensorflow:Enabling tensor equality
INFO:tensorflow:Enabling control flow v2

ما همچنین چند نام مستعار TFP مفید را تنظیم خواهیم کرد. انتزاعی جدید در حال حاضر در ارائه tfp.experimental.distribute و tfp.experimental.mcmc .

tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc

Root = tfed.JointDistributionCoroutine.Root

برای اتصال نوت بوک به TPU از کمکی زیر از JAX استفاده می کنیم. برای تأیید اتصال ما، تعداد دستگاه‌ها را چاپ می‌کنیم که باید هشت عدد باشد.

from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')

Found 8 devices

معرفی سریع به jax.pmap

پس از اتصال به یک TPU، ما دسترسی به هشت دستگاه داشته باشد. با این حال، زمانی که کد JAX را مشتاقانه اجرا می کنیم، JAX به طور پیش فرض محاسبات را روی یک مورد اجرا می کند.

ساده ترین راه برای اجرای یک محاسبات در بسیاری از دستگاه ها، ترسیم یک تابع است که هر دستگاه یک شاخص از نقشه را اجرا می کند. JAX فراهم می کند jax.pmap ( "نقشه موازی") تحول که تبدیل یک تابع را به یک است که نقشه های عملکرد را در چندین دستگاه.

در مثال زیر، آرایه‌ای به اندازه 8 ایجاد می‌کنیم (برای مطابقت با تعداد دستگاه‌های موجود) و تابعی را ترسیم می‌کنیم که 5 عدد به آن اضافه می‌کند.

xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)

<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5.  6.  7.  8.  9. 10. 11. 12.]

توجه داشته باشید که ما دریافت ShardedDeviceArray نوع تماس، نشان می دهد که آرایه خروجی به صورت فیزیکی در سراسر دستگاه تقسیم می شود.

jax.pmap عمل می کند معنایی مانند یک نقشه، اما دارای چند گزینه مهم است که رفتار خود را تغییر دهید. به طور پیش فرض، pmap فرض تمام ورودی به تابع در حال نقشه برداری بیش از، اما ما می توانیم این رفتار را با تغییر in_axes استدلال است.

xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)

[ 5.  6.  7.  8.  9. 10. 11. 12.]

شبیه از out_axes آرگومان به pmap تعیین اینکه آیا یا نه برای بازگشت به ارزش در هر دستگاه. تنظیم out_axes به None طور خودکار ارزش بر روی دستگاه 1 را برمی گرداند و تنها باید مورد استفاده قرار گیرد اگر ما با اعتماد به نفس ارزش همان در هر دستگاه هستند.

xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)

2.0

چه اتفاقی می‌افتد وقتی کاری که می‌خواهیم انجام دهیم به‌راحتی به‌عنوان یک تابع خالص نگاشت‌شده قابل بیان نباشد؟ به عنوان مثال، اگر بخواهیم در محوری که روی آن نقشه برداری می کنیم، جمع آوری کنیم، چطور؟ JAX "مجموعه ها" را ارائه می دهد، عملکردهایی که در بین دستگاه ها ارتباط برقرار می کنند تا نوشتن برنامه های توزیع شده جالب تر و پیچیده تر را امکان پذیر کند. برای درک اینکه دقیقا چگونه کار می کنند، SPMD را معرفی می کنیم.

SPMD چیست؟

داده های چندگانه تک برنامه ای (SPMD) یک مدل برنامه نویسی همزمان است که در آن یک برنامه واحد (یعنی همان کد) به طور همزمان در دستگاه ها اجرا می شود، اما ورودی های هر یک از برنامه های در حال اجرا می تواند متفاوت باشد.

اگر برنامه ما یک تابع ساده از ورودی های آن (یعنی چیزی شبیه به این است x + 5 )، اجرای یک برنامه در SPMD فقط نقشه برداری آن داده ها در طول های مختلف، مانند ما با انجام jax.pmap پیش از آن. با این حال، ما می‌توانیم کارهایی بیش از یک تابع انجام دهیم. JAX "مجموعه ها" را ارائه می دهد، که عملکردهایی هستند که بین دستگاه ها ارتباط برقرار می کنند.

به عنوان مثال، شاید ما بخواهیم مجموع یک مقدار را در تمام دستگاه های خود در نظر بگیریم. قبل از انجام این کار، ما نیاز به اختصاص یک نام به ما محور نقشه برداری هستید بیش از در pmap . پس از آن ما با استفاده از lax.psum ( "مجموع موازی") تابع برای انجام یک جمع در سراسر دستگاه، حصول اطمینان از ما شناسایی به نام محور ما در حال جمع.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)

ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)

psum مصالح جمعی ارزش x در هر دستگاه و هماهنگ ارزش خود را در سراسر نقشه یعنی out است 28. در هر دستگاه. ما دیگر یک «نقشه» ساده را انجام نمی‌دهیم، اما در حال اجرای یک برنامه SPMD هستیم که در آن محاسبات هر دستگاه اکنون می‌تواند با همان محاسبات روی دستگاه‌های دیگر تعامل داشته باشد، البته به روشی محدود با استفاده از مجموعه‌ها. در این سناریو، ما می توانیم استفاده out_axes = None ، چون psum خواهد شد که ارزش همگام سازی کنید.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))

ShardedDeviceArray(28., dtype=float32)

SPMD ما را قادر می سازد یک برنامه بنویسیم که بر روی هر دستگاهی در هر پیکربندی TPU به طور همزمان اجرا شود. همان کدی که برای انجام یادگیری ماشینی روی 8 هسته TPU استفاده می شود، می تواند روی یک پاد TPU که ممکن است صدها تا هزاران هسته داشته باشد، استفاده شود! برای یک آموزش مفصل تر در مورد jax.pmap و SPMD، شما می توانید به مراجعه JAX 101 آموزش .

MCMC در مقیاس

در این دفترچه، ما بر روی استفاده از روش‌های مونت کارلو زنجیره مارکوف (MCMC) برای استنتاج بیزی تمرکز می‌کنیم. ممکن است راه‌هایی وجود داشته باشد که از دستگاه‌های زیادی برای MCMC استفاده کنیم، اما در این نوت‌بوک، روی دو مورد تمرکز می‌کنیم:

1. اجرای زنجیره های مارکوف مستقل در دستگاه های مختلف. این مورد نسبتاً ساده است و انجام آن با وانیل TFP امکان پذیر است.
2. به اشتراک گذاری یک مجموعه داده در بین دستگاه ها. این مورد کمی پیچیده تر است و به ماشین آلات TFP اخیراً اضافه شده نیاز دارد.

زنجیر مستقل

فرض کنید می‌خواهیم با استفاده از MCMC استنتاج بیزی روی یک مشکل انجام دهیم و می‌خواهیم چندین زنجیره را به صورت موازی در چندین دستگاه اجرا کنیم (مثلاً 2 در هر دستگاه). معلوم می‌شود که این برنامه‌ای است که ما می‌توانیم فقط در دستگاه‌ها «نقشه‌برداری» کنیم، یعنی برنامه‌ای که نیازی به جمع ندارد. برای اطمینان از اینکه هر برنامه یک زنجیره مارکوف متفاوت را اجرا می کند (برخلاف اجرای یک زنجیره)، مقدار متفاوتی را برای دانه تصادفی به هر دستگاه ارسال می کنیم.

بیایید آن را روی یک مشکل اسباب بازی نمونه برداری از توزیع گاوسی دو بعدی امتحان کنیم. ما می توانیم از عملکرد موجود MCMC TFP خارج از جعبه استفاده کنیم. به طور کلی، ما سعی می کنیم بیشتر منطق را در عملکرد نقشه برداری خود قرار دهیم تا به وضوح بین آنچه در همه دستگاه ها در حال اجرا است در مقابل دستگاه اول تمایز قائل شویم.

def run(seed):
  target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob

  initial_state = jnp.zeros([2, 2]) # 2 chains
  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
  def trace_fn(state, pkr):
    return target_log_prob(state)

  states, log_prob = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    kernel=kernel,
    current_state=initial_state,
    trace_fn=trace_fn,
    seed=seed
  )
  return states, log_prob

به خودی خود، run تابع طول می کشد در یک دانه تصادفی بدون تابعیت (تا ببینید که چگونه بدون تابعیت کار اتفاقی، شما می توانید به عنوان خوانده شده TFP در JAX نوت بوک یا دیدن آموزش JAX 101 ). نقشه برداری run بیش از دانه های مختلف در حال اجرا چند زنجیره مارکوف مستقل خواهد شد.

states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)

(8, 1000, 2, 2) (8, 1000, 2)

توجه داشته باشید که چگونه ما اکنون یک محور اضافی مربوط به هر دستگاه داریم. می توانیم ابعاد را دوباره مرتب کنیم و آنها را صاف کنیم تا یک محور برای 16 زنجیره بدست آوریم.

states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])

fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()

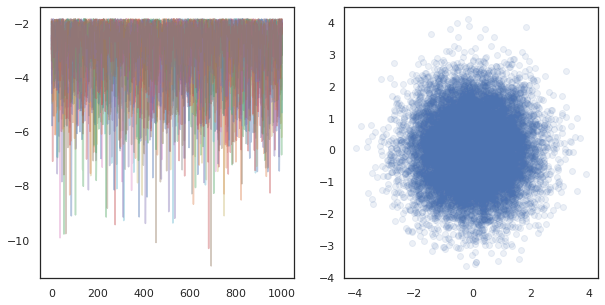
هنگامی که در حال اجرا زنجیره مستقل در بسیاری از دستگاه، آن را به عنوان آسان به عنوان pmap -ing بیش از یک تابع که با استفاده از tfp.mcmc ، حصول اطمینان از ما عبور مقادیر مختلف برای دانه تصادفی به هر دستگاه.

اشتراک گذاری داده ها

وقتی MCMC را انجام می‌دهیم، توزیع هدف اغلب یک توزیع پسین است که با شرطی کردن یک مجموعه داده به دست می‌آید، و محاسبه چگالی ورود به سیستم غیرعادی شامل جمع کردن احتمالات برای هر داده مشاهده‌شده است.

با مجموعه داده های بسیار بزرگ، حتی اجرای یک زنجیره روی یک دستگاه می تواند بسیار گران باشد. با این حال، وقتی به چندین دستگاه دسترسی داریم، می‌توانیم مجموعه داده را در بین دستگاه‌ها تقسیم کنیم تا از محاسباتی که در دسترس داریم بهتر استفاده کنیم.

اگر ما می خواهم به انجام MCMC با یک مجموعه داده sharded، ما نیاز به اطمینان از unnormalized ورود به سیستم با چگالی ما در هر دستگاه محاسبه نشان دهنده مجموع، یعنی چگالی بیش از همه داده ها، در غیر این صورت هر یک از دستگاه انجام خواهد MCMC با هدف نادرست خود را توزیع برای این منظور، بهره وری کل عوامل در حال حاضر ابزارهای جدید (یعنی tfp.experimental.distribute و tfp.experimental.mcmc ) است که قادر به محاسبه "sharded" احتمال ورود به سیستم و انجام MCMC با آنها.

توزیع های خرد شده

بر TFP انتزاع هسته در حال حاضر برای محاسبه probabiliities ورود به سیستم sharded است فراهم می کند Sharded متا توزیع، که طول می کشد یک توزیع به عنوان ورودی و یک توزیع جدید که دارای خواص خاص زمانی که در یک زمینه SPMD اعدام می گرداند. Sharded زندگی در tfp.experimental.distribute .

به طور مستقیم، یک Sharded مربوط توزیع به مجموعه ای از متغیرهای تصادفی که "تقسیم" در سراسر دستگاه بوده است. در هر دستگاه، آنها نمونه های مختلفی تولید می کنند و می توانند به صورت جداگانه دارای دانسیته ورود به سیستم متفاوتی باشند. روش دیگر، یک Sharded مربوط توزیع به "بشقاب" در مدل اصطلاح گرافیکی، که در آن اندازه صفحه تعداد دستگاه است.

نمونه برداری یک Sharded توزیع

اگر ما از یک نمونه Normal توزیع در یک برنامه در حال pmap اد با استفاده از دانه های مشابه بر روی هر دستگاه، ما را به نمونه های مشابه در هر دستگاه را دریافت کنید. می‌توانیم تابع زیر را به عنوان نمونه‌برداری از یک متغیر تصادفی که در بین دستگاه‌ها همگام‌سازی شده است، در نظر بگیریم.

# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
  return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                    -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32)

اگر ما بسته بندی tfd.Normal(0., 1.) با tfed.Sharded ، ما در حال حاضر منطقی هشت متغیر تصادفی مختلف (یکی در هر دستگاه) و در نتیجه تولید یک نمونه مختلف برای هر یک، با وجود عبور در دانه همان .

def f(seed, _):
  return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([ 1.2152631 ,  0.7818249 ,  0.32549605,  0.6828047 ,
                     1.3973192 , -0.57830244,  0.37862757,  2.7706041 ],                   dtype=float32)

یک نمایش معادل از این توزیع در یک دستگاه تنها 8 نمونه عادی مستقل است. هر چند ارزش از نمونه متفاوت خواهد بود ( tfed.Sharded کند شبه تصادفی تولید اعداد کمی متفاوت)، هر دو آنها نشان دهنده توزیع یکسان.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))

DeviceArray([ 0.08086783, -0.38624594, -0.3756545 ,  1.668957  ,
             -1.2758069 ,  2.1192007 , -0.85821325,  1.1305912 ],            dtype=float32)

با توجه به ورود چگالی یک Sharded توزیع

بیایید ببینیم چه اتفاقی می‌افتد وقتی که چگالی لگ یک نمونه را از یک توزیع معمولی در یک زمینه SPMD محاسبه می‌کنیم.

def f(seed, _):
  dist = tfd.Normal(0., 1.)
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                     -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32),
 ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
                     -0.94012403, -0.94012403, -0.94012403, -0.94012403],                   dtype=float32))

هر نمونه در هر دستگاه یکسان است، بنابراین ما چگالی یکسان را در هر دستگاه نیز محاسبه می کنیم. به طور شهودی، در اینجا ما فقط یک توزیع بر روی یک متغیر معمولی توزیع شده داریم.

با Sharded توزیع، ما باید یک توزیع بیش از 8 متغیرهای تصادفی، بنابراین زمانی که ما محاسبه log_prob از یک نمونه، ما خلاصه، در سراسر دستگاه، بیش از هر یک از تراکم ورود به سیستم منحصر به فرد. (شاید متوجه شوید که این مقدار کل log_prob بزرگتر از log_prob singleton محاسبه شده در بالا است.)

def f(seed, _):
  dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
    random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)

Sample: [ 1.2152631   0.7818249   0.32549605  0.6828047   1.3973192  -0.57830244
  0.37862757  2.7706041 ]
Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205
 -13.7349205 -13.7349205]

توزیع معادل، "نشقه نشده" همان چگالی ورود را تولید می کند.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)

DeviceArray(-13.7349205, dtype=float32)

Sharded توزیع مقادیر مختلف تولید از sample در هر دستگاه است، اما همان مقدار برای log_prob در هر دستگاه. اینجا چه خبره؟ Sharded توزیع می کند psum داخلی برای اطمینان از log_prob ارزش ها در هماهنگی در سراسر دستگاه می باشد. چرا این رفتار را می خواهیم؟ اگر ما در حال اجرا با همان سند MCMC در هر دستگاه، ما می خواهم target_log_prob به همان در سراسر هر دستگاه، حتی اگر برخی از متغیرهای تصادفی در محاسبه در سراسر دستگاه sharded.

علاوه بر این، Sharded تضمین می کند توزیع که شیب در سراسر دستگاه درست باشد، به اطمینان حاصل شود که الگوریتم های مانند شورای عالی رسانه ها، که به شیب تابع ورود به سیستم با چگالی به عنوان بخشی از تابع انتقال، تولید نمونه مناسب.

Sharded JointDistribution بازدید کنندگان

ما می توانیم مدل با متعدد ایجاد Sharded متغیرهای تصادفی با استفاده از JointDistribution بازدید کنندگان (JDS). متاسفانه، Sharded توزیع نمی تواند با خیال راحت با وانیل استفاده tfd.JointDistribution ، اما tfp.experimental.distribute صادرات "وصله" JDS که مانند رفتار خواهد شد Sharded توزیع.

def f(seed, _):
  dist = tfed.JointDistributionSequential([
    tfd.Normal(0., 1.),
    tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
  ])
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
                      1.6121525, 1.6121525, 1.6121525], dtype=float32),
  ShardedDeviceArray([ 0.8690128 , -0.83167845,  1.2209264 ,  0.88412696,
                       0.76478404, -0.66208494, -0.0129658 ,  0.7391483 ],                   dtype=float32)],
 ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
                     -12.214451, -12.214451, -12.214451, -12.214451],                   dtype=float32))

این JDS sharded می توانید هر دو Sharded توزیع و وانیل بهره وری کل عوامل به عنوان اجزای. برای توزیع‌های تکه‌ای نشده، نمونه‌های مشابهی را در هر دستگاه به‌دست می‌آوریم و برای توزیع‌های خرد شده، نمونه‌های متفاوتی دریافت می‌کنیم. log_prob در هر دستگاه است و همچنین هماهنگ شده است.

MCMC با Sharded توزیع

چگونه ما در مورد فکر می کنم Sharded توزیع در زمینه MCMC؟ اگر ما یک مدل مولد است که می تواند به عنوان یک ابراز کرده اند JointDistribution ، ما می توانیم برخی محور که مدل به "سفال" در سراسر انتخاب کنید. به طور معمول، یک متغیر تصادفی در مدل با داده‌های مشاهده‌شده مطابقت دارد، و اگر مجموعه داده‌ای بزرگ داشته باشیم که می‌خواهیم آن را در دستگاه‌ها تقسیم کنیم، می‌خواهیم متغیرهایی که به نقاط داده مرتبط هستند نیز تقسیم شوند. همچنین ممکن است متغیرهای تصادفی «محلی» داشته باشیم که با مشاهداتی که به اشتراک می‌گذاریم، یک به یک هستند، بنابراین باید آن متغیرهای تصادفی را نیز برش دهیم.

ما بیش از نمونه هایی از استفاده از رفتن Sharded توزیع با بهره وری کل عوامل MCMC در این بخش. ما با یک بیزی مثال رگرسیون لجستیک ساده شروع و نتیجه گیری با یک مثال فاکتور ماتریس، با هدف نشان دادن برخی استفاده از موارد برای distribute کتابخانه.

مثال: رگرسیون لجستیک بیزی برای MNIST

ما می خواهیم رگرسیون لجستیک بیزی را روی یک مجموعه داده بزرگ انجام دهیم. این مدل یک قبل \(p(\theta)\) بیش از وزن های رگرسیون، و احتمال \(p(y_i | \theta, x_i)\) است که بیش از همه داده ها خلاصه \(\{x_i, y_i\}_{i = 1}^N\) برای به دست آوردن کل چگالی ورود به سیستم مشترک. اگر ما داده های ما سفال، ما می خواهم متغیرهای تصادفی مشاهده سفال \(x_i\) و \(y_i\) در مدل ما.

ما از مدل رگرسیون لجستیک بیزی زیر برای طبقه بندی MNIST استفاده می کنیم:

\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]

بیایید MNIST را با استفاده از مجموعه داده های TensorFlow بارگیری کنیم.

mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.

raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.

Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1...
WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your
local data directory. If you'd instead prefer to read directly from our public
GCS bucket (recommended if you're running on GCP), you can instead pass
`try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`.
HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio…
Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.

ما 60000 تصویر آموزشی داریم اما بیایید از 8 هسته موجود خود استفاده کنیم و آن را به 8 روش تقسیم کنیم. ما این دستی را استفاده می کنید shard تابع مطلوبیت.

def shard_value(x):
  x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
  return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices

shard = functools.partial(jax.tree_map, shard_value)

sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)

(8, 7500, 784) (8, 7500)

قبل از ادامه، بیایید به سرعت در مورد دقت TPU و تأثیر آن بر HMC بحث کنیم. TPU ها اجرا ضرب ماتریس با استفاده از کم bfloat16 دقت برای سرعت. bfloat16 ضرب ماتریس اغلب برای بسیاری از برنامه های کاربردی یادگیری عمیق کافی است، اما زمانی که با شورای عالی رسانه ها استفاده می شود، ما به طور تجربی در بر داشت با دقت کمتر می توانید به واگرا مدار، باعث رد شود. ما می‌توانیم از ضرب‌های ماتریس با دقت بالاتر، به قیمت محاسبات اضافی استفاده کنیم.

برای افزایش دقت matmul ما، ما می توانید استفاده jax.default_matmul_precision دکوراتور با "tensorfloat32" دقت (برای دقت و حتی بالاتر ما می تواند استفاده "float32" دقت).

اکنون بیایید ما را تعریف run تابع، که در یک دانه تصادفی خواهد (که همان خواهد شد در هر دستگاه) و تکه های شکسته MNIST. تابع مدل فوق را پیاده سازی می کند و سپس از عملکرد وانیلی MCMC TFP برای اجرای یک زنجیره استفاده می کنیم. ما مطمئن شوید که برای تزئین run با jax.default_matmul_precision دکوراتور مطمئن شوید ضرب ماتریس است که با دقت بالاتر اجرا شود، هر چند در مثال خاص زیر، ما فقط به عنوان به خوبی می تواند با استفاده از jnp.dot(images, w, precision=lax.Precision.HIGH) .

# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device. 
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
  images, labels = data # a sharded dataset
  num_examples, dim = images.shape
  num_classes = 10

  def model_fn():
    w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
    b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
    logits = jnp.dot(images, w) + b
    yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
                       shard_axis_name='data')
  model = tfed.JointDistributionCoroutine(model_fn)

  init_seed, sample_seed = random.split(seed)

  initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`

  def target_log_prob(*state):
    return model.log_prob((*state, labels))

  def accuracy(w, b):
    logits = images.dot(w) + b
    preds = logits.argmax(axis=-1)
    # We take the average accuracy across devices by using `lax.pmean`
    return lax.pmean((preds == labels).mean(), 'data')

  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
  kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
  def trace_fn(state, pkr):
    return (
        target_log_prob(*state),
        accuracy(*state),
        pkr.new_step_size)
  states, trace = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    current_state=initial_state,
    kernel=kernel,
    trace_fn=trace_fn,
    seed=sample_seed
  )
  return states, trace

jax.pmap شامل یک کامپایل JIT اما تابع وارد شده است بعد از اولین تماس ذخیره سازی. ما پاسخ run و چشم پوشی از خروجی به کش تلفیقی.

%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s
Wall time: 1min 54s

حال به سراغ پاسخ run دوباره به ببینید که چه مدت طول می کشد اجرای واقعی.

%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s
Wall time: 1min 43s

ما در حال اجرای 200000 مرحله جهشی هستیم که هر یک از آنها یک گرادیان را در کل مجموعه داده محاسبه می کند. تقسیم محاسبات بر روی 8 هسته ما را قادر می سازد معادل 200000 دوره آموزشی را در حدود 95 ثانیه محاسبه کنیم، یعنی حدود 2100 دوره در ثانیه!

بیایید log-density هر نمونه و دقت هر نمونه را رسم کنیم:

fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()

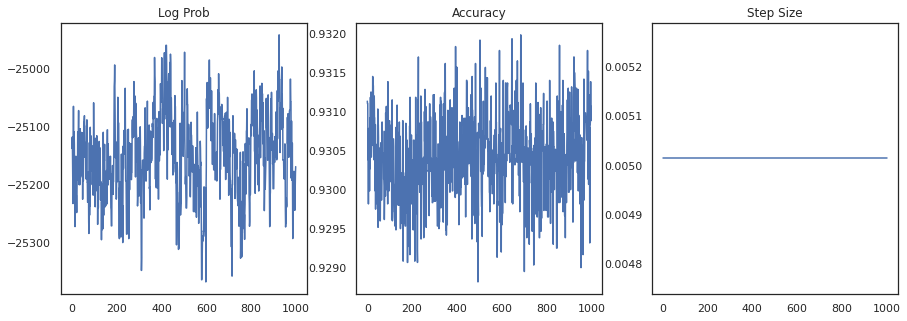
اگر نمونه ها را جمع آوری کنیم، می توانیم میانگین مدل بیزی را برای بهبود عملکرد خود محاسبه کنیم.

@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
  images, labels = data
  logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
  probs = jax.nn.softmax(logits, axis=-1)
  bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
  avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
  return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')

sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')

Average Accuracy: 0.9188529253005981
BMA Accuracy: 0.9264000058174133
Accuracy Improvement: 0.0075470805168151855

میانگین مدل بیزی دقت ما را تقریباً 1٪ افزایش می دهد!

مثال: سیستم توصیه MovieLens

اکنون بیایید با مجموعه داده توصیه های MovieLens که مجموعه ای از کاربران و رتبه بندی آنها از فیلم های مختلف است، استنتاج کنیم. به طور خاص، ما می توانیم MovieLens به عنوان یک نماینده \(N \times M\) ماتریس ساعت \(W\) که در آن \(N\) است که تعداد کاربران و \(M\) تعداد فیلم است. ما انتظار داریم \(N > M\). ورودی های \(W_{ij}\) یک بولی که نشان میدهد آیا کاربران \(i\) تماشا فیلم \(j\). توجه داشته باشید که MovieLens رتبه‌بندی‌های کاربران را ارائه می‌کند، اما برای ساده‌تر کردن مشکل، آن‌ها را نادیده می‌گیریم.

ابتدا مجموعه داده را بارگذاری می کنیم. ما از نسخه با 1 میلیون رتبه استفاده خواهیم کرد.

movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
          'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
          'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
          'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']

Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0...
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl…

HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value='')))
Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord
HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value='')))
Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.

ما برخی از پیش پردازش از مجموعه داده را انجام دهد به دست آوردن ماتریس ساعت \(W\).

raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']

movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])

num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1

movie_titles = dict(zip(movielens['train']['movie_id'],
                        movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
                        genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
                     for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]

watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)

(6040, 3706)

ما می توانیم یک مدل مولد برای تعریف \(W\)، با استفاده از یک مدل فاکتور ماتریس احتمالی ساده است. فرض کنیم یک نهفته \(N \times D\) ماتریس کاربران \(U\) و نهان \(M \times D\) ماتریس فیلم \(V\)، که هنگامی که ضرب ماتریس برای تولید ساعت مچی logits یک برنولی \(W\). ما همچنین شامل یک بردار تعصب برای کاربران و فیلم، \(u\) و \(v\).

\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]

این یک ماتریس بسیار بزرگ است. 6040 کاربر و 3706 فیلم منجر به ماتریسی با بیش از 22 میلیون ورودی در آن می شود. چگونه به اشتراک گذاری این مدل نزدیک شویم؟ خب، اگر فرض کنیم که \(N > M\) (یعنی کاربران بیش از فیلم وجود دارد)، و سپس آن را حس به سفال ماتریس ساعت در سراسر محور کاربران، بنابراین هر دستگاه را یک تکه از ماتریس ساعت مربوط به یک زیر مجموعه از کاربران . بر خلاف مثال قبلی، با این حال، ما نیز به سفال تا دارند \(U\) ماتریس، از آن است که تعبیه برای هر کاربر، بنابراین هر یک از دستگاه مسئول تکه های شکسته خواهد \(U\) و تکه های شکسته \(W\). از سوی دیگر، \(V\) unsharded خواهد بود و توان در سراسر دستگاه هماهنگ شده است.

sharded_watch_matrix = shard(watch_matrix)

قبل از اینکه ما ارسال ما run ، اجازه دهید به سرعت بحث در مورد چالش های اضافی با sharding محلی متغیر تصادفی \(U\). هنگامی که در حال اجرا HMC، وانیل tfp.mcmc.HamiltonianMonteCarlo هسته نمونه خواهد تکانه برای هر عنصر از دولت زنجیره ای است. پیش از این، تنها متغیرهای تصادفی تقسیم نشده بخشی از آن حالت بودند و لحظه لحظه در هر دستگاه یکسان بود. هنگامی که ما در حال حاضر sharded دارند \(U\)، ما نیاز به نمونه تکانه های مختلف در هر دستگاه برای \(U\)، در حالی که نمونه برداری از تکانه برای \(V\). برای انجام این کار، ما می توانیم با استفاده از tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo با Sharded توزیع حرکت. همانطور که ما به محاسبات موازی درجه یک ادامه می دهیم، ممکن است این را ساده کنیم، به عنوان مثال با گرفتن یک نشانگر تیرگی به هسته HMC.

def make_run(*,
             axis_name,
             dim=20,
             num_chains=2,
             prior_variance=1.,
             step_size=1e-2,
             num_leapfrog_steps=100,
             num_burnin_steps=1000,
             num_results=500,
             ):
  @functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
  @jax.default_matmul_precision('tensorfloat32')
  def run(key, watch_matrix):
    num_users, num_movies = watch_matrix.shape

    Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)

    def prior_fn():
      user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
      user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
      movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
      movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
      return (user_embeddings, user_bias, movie_embeddings, movie_bias)
    prior = tfed.JointDistributionCoroutine(prior_fn)

    def model_fn():
      user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
      logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
                + user_bias[..., :, None] + movie_bias[..., None, :])
      yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
    model = tfed.JointDistributionCoroutine(model_fn)

    init_key, sample_key = random.split(key)
    initial_state = prior.sample(seed=init_key, sample_shape=num_chains)

    def target_log_prob(*state):
      return model.log_prob((*state, watch_matrix))

    momentum_distribution = tfed.JointDistributionSequential([
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
    ])

    # We pass in momentum_distribution here to ensure that the momenta for 
    # user_embeddings and user_bias are also sharded
    kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
                                                      num_leapfrog_steps,
                                                      momentum_distribution=momentum_distribution)

    num_adaptation_steps = int(0.8 * num_burnin_steps)
    kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)

    def trace_fn(state, pkr):
      return {
        'log_prob': target_log_prob(*state),
        'log_accept_ratio': pkr.inner_results.log_accept_ratio,
      }
    return tfm.sample_chain(
        num_results, initial_state,
        kernel=kernel,
        num_burnin_steps=num_burnin_steps,
        trace_fn=trace_fn,
        seed=sample_key)
  return run

ما دوباره آن را اجرا کنید یک بار به کش وارد run .

%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 56 s, sys: 1min 24s, total: 2min 20s
Wall time: 3min 35s

اکنون آن را دوباره بدون سربار کامپایل اجرا می کنیم.

%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s
Wall time: 3min 1s

به نظر می رسد که ما حدود 150000 مرحله جهشی را در حدود 3 دقیقه تکمیل کرده ایم، بنابراین حدود 83 مرحله جهشی در ثانیه! بیایید نسبت پذیرش و چگالی لگ نمونه های خود را رسم کنیم.

fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
  ax.plot(val[0]) # Indexing into a sharded array, each element is the same
  ax.set_title(key);

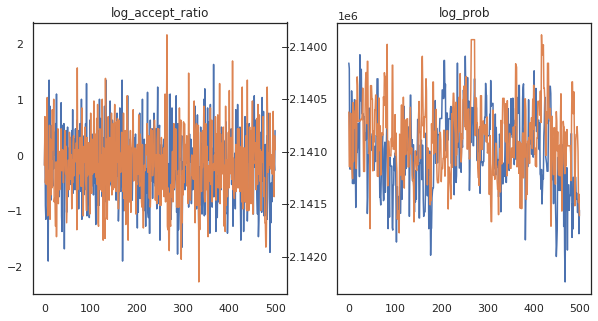
اکنون که چند نمونه از زنجیره مارکوف خود داریم، بیایید از آنها برای پیش‌بینی استفاده کنیم. ابتدا اجازه دهید هر یک از اجزا را استخراج کنیم. به یاد داشته باشید که user_embeddings و user_bias هستند تقسیم در دستگاه، بنابراین ما نیاز به الحاق ما ShardedArray به همه آنها را به دست آورد. از سوی دیگر، movie_embeddings و movie_bias همان در هر دستگاه است، بنابراین ما فقط می توانید مقدار از سفال اولین انتخاب کنید. ما به طور منظم استفاده numpy برای کپی از مقادیر تماس TPU ها را به پردازنده.

user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')

User embeddings: (500, 2, 6040, 20)
User bias: (500, 2, 6040)
Movie embeddings: (500, 2, 3706, 20)
Movie bias: (500, 2, 3706)

بیایید سعی کنیم یک سیستم توصیه گر ساده بسازیم که از عدم قطعیت ثبت شده در این نمونه ها استفاده کند. بیایید ابتدا تابعی بنویسیم که فیلم ها را بر اساس احتمال تماشا رتبه بندی می کند.

@jax.jit
def recommend(sample, user_id):
  user_embeddings, user_bias, movie_embeddings, movie_bias = sample
  movie_logits = (
      jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
      + user_bias[user_id] + movie_bias)
  return movie_logits.argsort()[::-1]

اکنون می‌توانیم تابعی بنویسیم که روی همه نمونه‌ها حلقه بزند و برای هر یک، فیلم رتبه‌بندی شده برتر را که کاربر قبلاً تماشا نکرده است، انتخاب کند. سپس می‌توانیم تعداد فیلم‌های پیشنهادی را در بین نمونه‌ها ببینیم.

def get_recommendations(user_id): 
  movie_ids = []
  already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
  for i in range(500):
    for j in range(2):
      sample = jax.tree_map(lambda x: x[i, j], samples)
      ranking = recommend(sample, user_id)
      for movie_id in ranking:
        if int(movie_id) not in already_watched:
          movie_ids.append(movie_id)
          break
  return movie_ids

def plot_recommendations(movie_ids, ax=None):
  titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
  ax = ax or plt.gca()
  names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
  ax.bar(names, counts)
  ax.set_xticklabels(names, rotation=90)

بیایید کاربری را که بیشترین فیلم را دیده در مقابل شخصی که کمترین فیلم را دیده است، در نظر بگیریم.

user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])

2314 20

ما امیدواریم که سیستم ما است اطمینان بیشتری در مورد user_most از user_least ، با توجه به اینکه ما باید اطلاعات بیشتری در مورد اینکه چه نوع از فیلم user_most بیشتر احتمال دارد به تماشا.

fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');

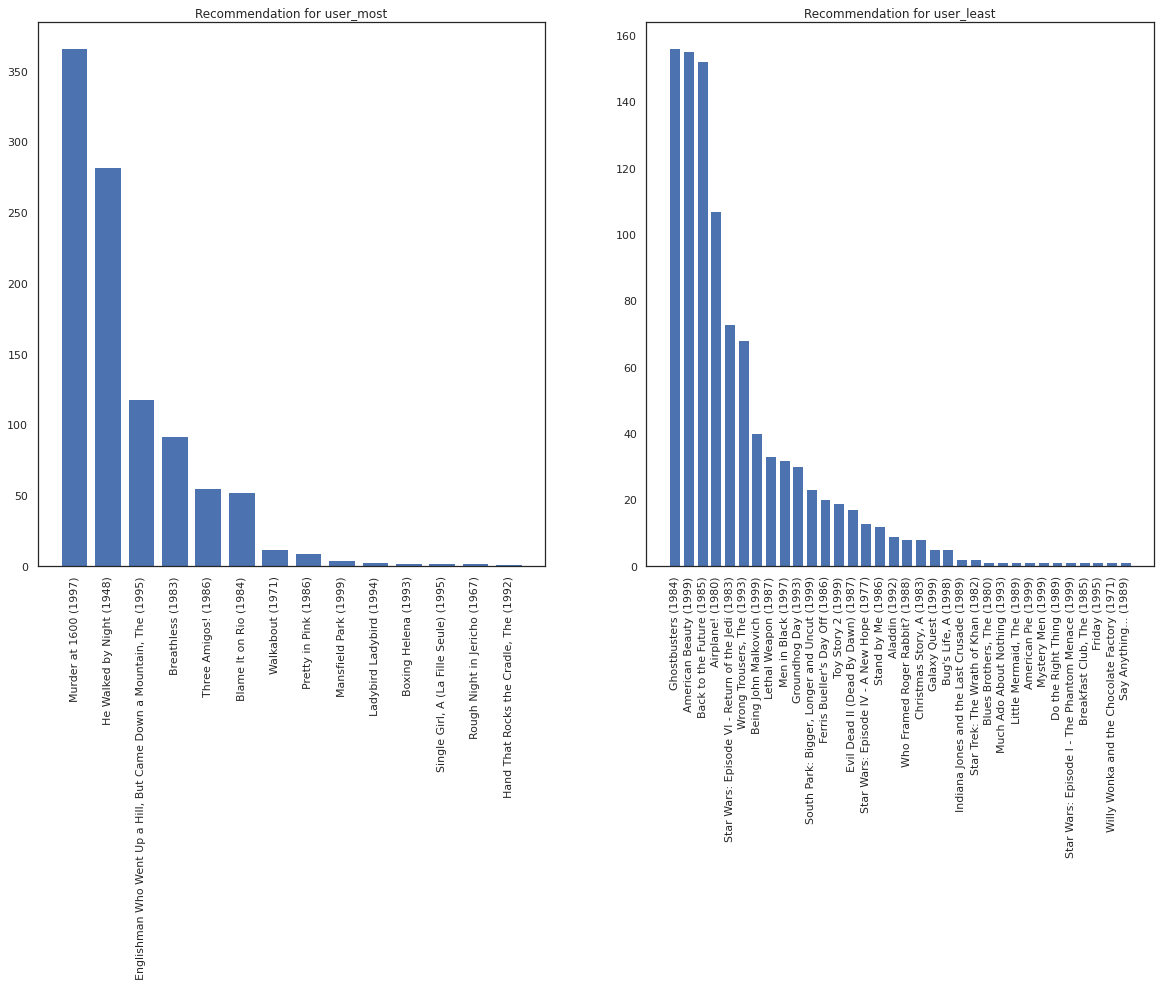
ما می بینیم این است که واریانس در توصیه های ما برای وجود دارد user_least منعکس عدم قطعیت اضافی ما در تنظیمات سازمان دیده بان خود.

همچنین می‌توانیم نگاهی به ژانرهای فیلم‌های پیشنهادی داشته باشیم.

most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');

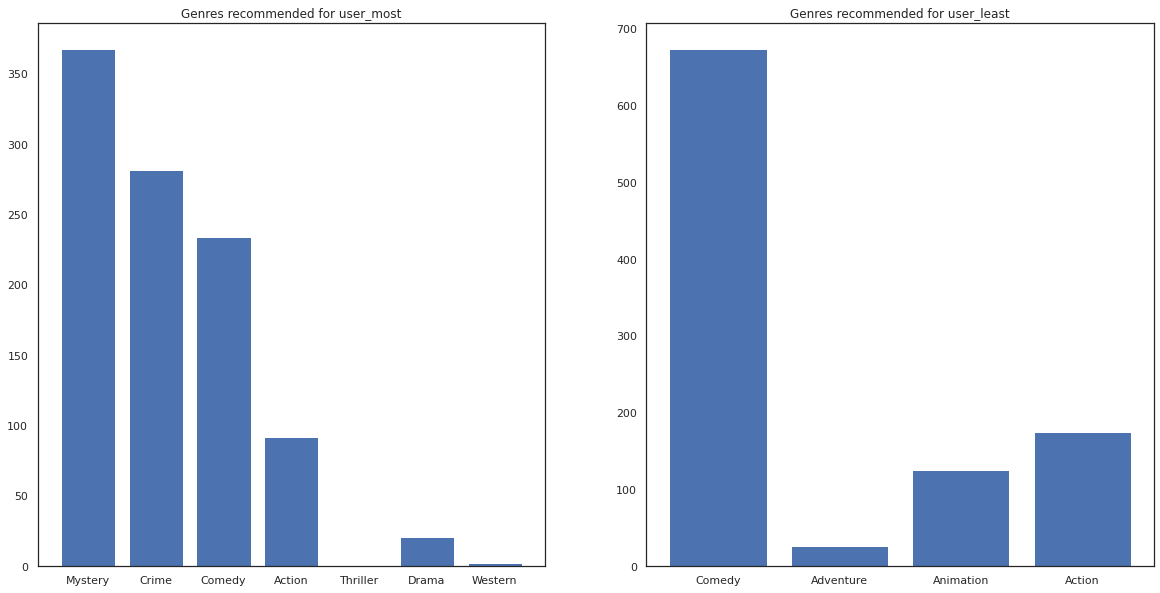
user_most دیده است بسیاری از فیلم ها و ژانرهای است طاقچه مانند رمز و راز و جرم و جنایت توصیه شده است در حالی که user_least است بسیاری از فیلم را تماشا نیست و فیلم بیشتر جریان اصلی، که کمدی و اکشن چوله توصیه شده است.