TensorFlow.org এ দেখুন

Google Colab-এ চালান

GitHub-এ উৎস দেখুন

নোটবুক ডাউনলোড করুন

JAX-এ TensorFlow সম্ভাব্যতা (TFP) এখন বিতরণ করা সংখ্যাসূচক কম্পিউটিংয়ের জন্য সরঞ্জাম রয়েছে। বৃহৎ সংখ্যক এক্সিলারেটরের স্কেল করার জন্য, টুলগুলি "একক-প্রোগ্রাম মাল্টিপল-ডেটা" দৃষ্টান্ত, বা সংক্ষেপে SPMD ব্যবহার করে কোড লেখার চারপাশে তৈরি করা হয়।

এই নোটবুকে, আমরা কীভাবে "এসপিএমডি-তে ভাবতে হয়" এবং টিপিইউ পড বা জিপিইউ-এর ক্লাস্টারগুলির মতো কনফিগারেশনে স্কেলিং করার জন্য নতুন TFP বিমূর্ততাগুলি প্রবর্তন করব। আপনি যদি এই কোডটি নিজে চালান, তাহলে একটি TPU রানটাইম নির্বাচন করতে ভুলবেন না।

আমরা প্রথমে সর্বশেষ সংস্করণ TFP, JAX এবং TF ইনস্টল করব।

ইন্সটল করে

pip install jaxlib --upgrade -q 2>&1 1> /dev/null
pip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/null
pip install tf-nightly-cpu -q -I 2>&1 1> /dev/null
pip install jax -I -q --upgrade 2>&1 1>/dev/null

আমরা কিছু JAX ইউটিলিটি সহ কিছু সাধারণ লাইব্রেরি আমদানি করব।

সেটআপ এবং আমদানি

import functools
import collections
import contextlib

import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds

from tensorflow_probability.substrates import jax as tfp

sns.set(style='white')

INFO:tensorflow:Enabling eager execution
INFO:tensorflow:Enabling v2 tensorshape
INFO:tensorflow:Enabling resource variables
INFO:tensorflow:Enabling tensor equality
INFO:tensorflow:Enabling control flow v2

আমরা কিছু সহজ TFP উপনামও সেট আপ করব৷ নতুন বিমূর্ত বর্তমানে প্রদান করা হয় tfp.experimental.distribute এবং tfp.experimental.mcmc ।

tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc

Root = tfed.JointDistributionCoroutine.Root

নোটবুকটিকে একটি TPU এর সাথে সংযুক্ত করতে, আমরা JAX থেকে নিম্নলিখিত সাহায্যকারী ব্যবহার করি৷ আমরা সংযুক্ত আছি তা নিশ্চিত করতে, আমরা ডিভাইসের সংখ্যা প্রিন্ট করি, যা আটটি হওয়া উচিত।

from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')

Found 8 devices

জন্য একটি দ্রুত ভূমিকা jax.pmap

একটি নমনীয় সাথে সংযোগ করার পর, আমরা আট ডিভাইসের এক্সেস আছে। যাইহোক, যখন আমরা JAX কোডটি সাগ্রহে চালাই, তখন JAX ডিফল্ট হয় শুধুমাত্র একটিতে কম্পিউটেশন চালাতে।

অনেক ডিভাইস জুড়ে একটি গণনা চালানোর সবচেয়ে সহজ উপায় হল একটি ফাংশন ম্যাপ করা, প্রতিটি ডিভাইস মানচিত্রের একটি সূচী সম্পাদন করে। Jax উপলব্ধ jax.pmap ( "সমান্তরাল মানচিত্র") রূপান্তর যা এক বিভিন্ন ডিভাইস জুড়ে ফাংশন মানচিত্র যে মধ্যে একটি ফাংশন সক্রিয়।

নিম্নলিখিত উদাহরণে, আমরা 8 আকারের একটি অ্যারে তৈরি করি (উপলব্ধ ডিভাইসের সংখ্যার সাথে মেলে) এবং একটি ফাংশন ম্যাপ করি যা এটি জুড়ে 5 যোগ করে।

xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)

<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5.  6.  7.  8.  9. 10. 11. 12.]

নোট আমরা পাওয়া ShardedDeviceArray টাইপ পিছনে, যা নির্দেশ করে আউটপুট অ্যারে শারীরিকভাবে ডিভাইস জুড়ে বিভক্ত করা হয়।

jax.pmap শব্দার্থগতভাবে একটি মানচিত্র মত কাজ করে, কিন্তু কিছু গুরুত্বপূর্ণ অপশন তার আচরণ পরিবর্তন যে হয়েছে। ডিফল্টরূপে, pmap অনুমান ফাংশন সমস্ত ইনপুট উপর ম্যাপ হচ্ছে, কিন্তু আমরা এই আচরণ পরিবর্তন করতে পারেন in_axes যুক্তি।

xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)

[ 5.  6.  7.  8.  9. 10. 11. 12.]

অনুরূপভাবে, out_axes আর্গুমেন্ট প্রাপ্ত করতে pmap কিনা তা নির্ধারণ করে প্রত্যেকটি ডিভাইসে মান দেখাবে। সেট out_axes করার None স্বয়ংক্রিয়ভাবে 1st ডিভাইসে মান এবং কেবল যদি আমরা আত্মবিশ্বাসী মান যে ডিভাইসে একই হয় ব্যবহার করা উচিত।

xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)

2.0

আমরা যা করতে চাই তা ম্যাপ করা বিশুদ্ধ ফাংশন হিসাবে সহজে প্রকাশযোগ্য না হলে কী ঘটে? উদাহরণস্বরূপ, যদি আমরা অক্ষ জুড়ে একটি সমষ্টি করতে চাই যা আমরা ম্যাপিং করছি? JAX আরও আকর্ষণীয় এবং জটিল বিতরণ করা প্রোগ্রাম লেখার জন্য সক্ষম করার জন্য "সম্মিলিত", ফাংশনগুলি অফার করে যা ডিভাইস জুড়ে যোগাযোগ করে। তারা ঠিক কিভাবে কাজ করে তা বোঝার জন্য, আমরা SPMD পরিচয় করিয়ে দেব।

SPMD কি?

একক-প্রোগ্রাম মাল্টিপল-ডেটা (SPMD) হল একটি সমসাময়িক প্রোগ্রামিং মডেল যেখানে একটি একক প্রোগ্রাম (অর্থাৎ একই কোড) একই সাথে ডিভাইস জুড়ে কার্যকর করা হয়, কিন্তু চলমান প্রতিটি প্রোগ্রামের ইনপুট ভিন্ন হতে পারে।

তাহলে আমাদের প্রোগ্রাম তার ইনপুট একটি সহজ ফাংশন (যেমন অর্থাত কিছু x + 5 ), SPMD মধ্যে একটি প্রোগ্রাম ব্যবহার করছেন তা শুধু এটি উপর বিভিন্ন তথ্য ম্যাপিং করা হয়, মনে হচ্ছে আমরা করেছিল jax.pmap আগে। যাইহোক, আমরা একটি ফাংশনকে "ম্যাপ" করার চেয়ে আরও বেশি কিছু করতে পারি। JAX "সমষ্টিগত" অফার করে, যা এমন ফাংশন যা ডিভাইস জুড়ে যোগাযোগ করে।

উদাহরণস্বরূপ, হয়তো আমরা আমাদের সমস্ত ডিভাইস জুড়ে একটি পরিমাণের যোগফল নিতে চাই। আগে আমরা তা করতে, আমরা একটি নাম নির্ধারণ করতে আমরা ওখানে ম্যাপিং অক্ষ প্রয়োজন pmap । আমরা তখন ব্যবহার lax.psum ডিভাইস জুড়ে একটি সমষ্টি সম্পাদন করতে ( "সমান্তরাল সমষ্টি") ফাংশন, আমরা চিহ্নিত নামে অক্ষ আমরা ধরে summing করছি নিশ্চিত।

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)

ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)

psum সমষ্টিগত দলা মান x প্রতিটি ডিভাইস চালু এবং সিঙ্ক্রোনাইজ মানচিত্র জুড়ে এর মান অর্থাৎ out হয় 28. প্রতিটি ডিভাইসে। আমরা আর একটি সাধারণ "মানচিত্র" সম্পাদন করছি না, তবে আমরা একটি SPMD প্রোগ্রাম চালাচ্ছি যেখানে প্রতিটি ডিভাইসের গণনা এখন অন্যান্য ডিভাইসে একই গণনার সাথে ইন্টারঅ্যাক্ট করতে পারে, যদিও সীমিত উপায়ে সমষ্টি ব্যবহার করে। এই পরিস্থিতিতে, আমরা ব্যবহার করতে পারি out_axes = None , কারণ psum মান সুসংগত করা হবে।

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))

ShardedDeviceArray(28., dtype=float32)

SPMD আমাদেরকে একটি প্রোগ্রাম লিখতে সক্ষম করে যা একই সাথে যেকোনো TPU কনফিগারেশনে প্রতিটি ডিভাইসে চালানো হয়। 8 টি টিপিইউ কোরে মেশিন লার্নিং করার জন্য যে কোডটি ব্যবহার করা হয় সেই একই কোড টিপিইউ পডে ব্যবহার করা যেতে পারে যাতে কয়েকশ থেকে হাজার কোর থাকতে পারে! সম্পর্কে আরো বিস্তারিত টিউটোরিয়াল জন্য jax.pmap এবং SPMD, আপনি উল্লেখ করতে পারেন Jax 101 টিউটোরিয়াল ।

স্কেলে MCMC

এই নোটবুকে, আমরা বায়েসিয়ান ইনফারেন্সের জন্য মার্কভ চেইন মন্টে কার্লো (MCMC) পদ্ধতি ব্যবহার করার উপর ফোকাস করি। MCMC এর জন্য আমরা অনেক ডিভাইস ব্যবহার করার উপায় আছে, কিন্তু এই নোটবুকে, আমরা দুটির উপর ফোকাস করব:

1. বিভিন্ন ডিভাইসে স্বাধীন মার্কভ চেইন চালানো। এই কেসটি মোটামুটি সহজ এবং ভ্যানিলা TFP দিয়ে করা সম্ভব।
2. ডিভাইস জুড়ে একটি ডেটাসেট ভাগ করা। এই কেসটি একটু বেশি জটিল এবং এর জন্য সম্প্রতি যোগ করা TFP যন্ত্রপাতি প্রয়োজন৷

স্বাধীন চেইন

বলুন আমরা MCMC ব্যবহার করে একটি সমস্যা নিয়ে Bayesian অনুমান করতে চাই এবং বেশ কয়েকটি ডিভাইস জুড়ে সমান্তরালভাবে কয়েকটি চেইন চালাতে চাই (প্রতিটি ডিভাইসে 2 বলুন)। এটি এমন একটি প্রোগ্রাম হিসাবে দেখা যাচ্ছে যা আমরা সমস্ত ডিভাইস জুড়ে কেবল "ম্যাপ" করতে পারি, অর্থাত্ যেটির কোনও সমষ্টির প্রয়োজন নেই৷ প্রতিটি প্রোগ্রাম একটি ভিন্ন মার্কভ চেইন (একটি চালানোর বিপরীতে) কার্যকর করে তা নিশ্চিত করতে, আমরা প্রতিটি ডিভাইসে এলোমেলো বীজের জন্য আলাদা মান দিয়ে থাকি।

2-ডি গাউসিয়ান ডিস্ট্রিবিউশন থেকে নমুনা নেওয়ার একটি খেলনা সমস্যা নিয়ে এটি চেষ্টা করা যাক। আমরা TFP এর বিদ্যমান MCMC কার্যকারিতা বাক্সের বাইরে ব্যবহার করতে পারি। সাধারণভাবে, আমরা আমাদের ম্যাপ করা ফাংশনের ভিতরে বেশিরভাগ যুক্তি রাখার চেষ্টা করি যাতে সমস্ত ডিভাইসে কি চলছে বনাম প্রথমটির মধ্যে আরও স্পষ্টভাবে পার্থক্য করা যায়।

def run(seed):
  target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob

  initial_state = jnp.zeros([2, 2]) # 2 chains
  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
  def trace_fn(state, pkr):
    return target_log_prob(state)

  states, log_prob = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    kernel=kernel,
    current_state=initial_state,
    trace_fn=trace_fn,
    seed=seed
  )
  return states, log_prob

নিজে, run ফাংশন একটি আড়ম্বরহীন র্যান্ডম বীজ লাগে (দেখুন কিভাবে আড়ম্বরহীন যদৃচ্ছতা কাজ, আপনি পড়তে পারেন Jax উপর TFP নোটবুক বা দেখতে Jax 101 টিউটোরিয়াল )। ম্যাপিং run বিভিন্ন বীজ অনেকগুলি স্বাধীন মার্কভ চেইন চালাতে হবে।

states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)

(8, 1000, 2, 2) (8, 1000, 2)

এখন প্রতিটি ডিভাইসের সাথে সম্পর্কিত একটি অতিরিক্ত অক্ষ রয়েছে তা নোট করুন। 16টি চেইনের জন্য একটি অক্ষ পেতে আমরা মাত্রাগুলিকে পুনরায় সাজাতে পারি এবং তাদের সমতল করতে পারি।

states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])

fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()

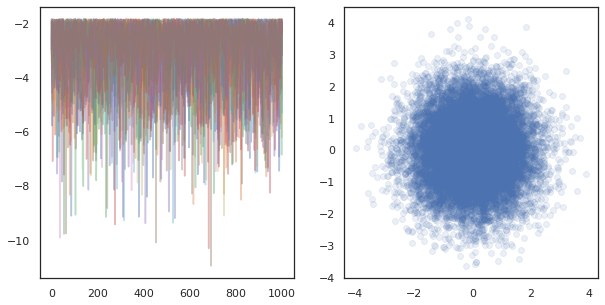
যখন অনেক ডিভাইসের স্বাধীন চেইন চলমান, এটি হিসাবে সহজ হিসাবে pmap একটি ফাংশন যে ব্যবহারসমূহ উপর -ing tfp.mcmc নিশ্চিত আমরা একে ডিভাইসে র্যান্ডম বীজ জন্য আলাদা মান পাস।

তথ্য ভাগ করা

যখন আমরা MCMC করি, টার্গেট ডিস্ট্রিবিউশন প্রায়শই একটি ডেটাসেটে কন্ডিশনার দ্বারা প্রাপ্ত একটি পোস্টেরিয়র ডিস্ট্রিবিউশন হয় এবং একটি অস্বাভাবিক লগ-ঘনত্ব গণনা করা প্রতিটি পর্যবেক্ষণ করা ডেটার সম্ভাব্যতা যোগ করে।

খুব বড় ডেটাসেটের সাথে, এটি একটি একক ডিভাইসে একটি চেইন চালানো নিষেধমূলকভাবে ব্যয়বহুল হতে পারে। যাইহোক, যখন আমাদের একাধিক ডিভাইসে অ্যাক্সেস থাকে, তখন আমরা উপলব্ধ গণনাটি আরও ভালভাবে লাভ করতে আমরা সমস্ত ডিভাইস জুড়ে ডেটাসেটকে বিভক্ত করতে পারি।

আমরা একটি sharded ডেটা সেটটি সঙ্গে এমসিএমসি করতে চান তাহলে, এটি করার জন্য unnormalized লগ-ঘনত্ব আমরা একে ডিভাইসে গনা মোট, অর্থাত্ সব ডেটার উপর ঘনত্ব প্রতিনিধিত্ব করে প্রয়োজন, অন্যথায় প্রতিটি যন্ত্রের তাদের নিজস্ব ভুল লক্ষ্য সঙ্গে এমসিএমসি কাজ করা হবে বিতরণ এই শেষ, TFP এখন (অর্থাত নতুন সরঞ্জামগুলি হয়েছে tfp.experimental.distribute এবং tfp.experimental.mcmc ) যে কম্পিউটিং "sharded" লগ সম্ভাব্যতা সক্ষম এবং তাদের সঙ্গে এমসিএমসি করছেন।

শেয়ার্ড ডিস্ট্রিবিউশন

কোর বিমূর্ততা TFP এখন কম্পিউটিং sharded লগ probabiliities জন্য প্রদান করে Sharded মেটা-বন্টন, যা ইনপুট হিসাবে একটি বিতরণ নেয় এবং নতুন ডিস্ট্রিবিউশন একটি SPMD প্রেক্ষাপটে মৃত্যুদন্ড কার্যকর নির্দিষ্ট বৈশিষ্ট্য আছে যে ফেরৎ। Sharded এ থাকেন tfp.experimental.distribute ।

Intuitively, একটি Sharded র্যান্ডম ভেরিয়েবল হয়েছেন এমন একটি সেটের ডিভাইস জুড়ে "বিভাজিত" হয়েছে বন্টন অনুরূপ। প্রতিটি ডিভাইসে, তারা বিভিন্ন নমুনা তৈরি করবে এবং পৃথকভাবে বিভিন্ন লগ-ঘনত্ব থাকতে পারে। অন্যথা, একটি Sharded একটি "প্লেট" গ্রাফিক্যাল মডেল বাচনে, যেখানে প্লেট আকার ডিভাইসের সংখ্যা বিতরণের অনুরূপ।

একটি স্যাম্পলিং Sharded বন্টন

আমরা একটি থেকে নমুনা তাহলে Normal একটি প্রোগ্রাম হচ্ছে বন্টন pmap প্রতিটি ডিভাইসে একই বীজ ব্যবহার -ed, আমরা প্রতিটি ডিভাইসে একই নমুনা পাবেন। আমরা নিম্নলিখিত ফাংশনটিকে একটি একক র্যান্ডম ভেরিয়েবলের নমুনা হিসাবে ভাবতে পারি যা ডিভাইস জুড়ে সিঙ্ক্রোনাইজ করা হয়।

# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
  return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                    -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32)

আমরা যদি মোড়ানো tfd.Normal(0., 1.) একটি সঙ্গে tfed.Sharded , আমরা কথাটি এখন আট বিভিন্ন র্যান্ডম ভেরিয়েবল আছে (প্রতিটি ডিভাইসে একটি) এবং সেইজন্য একই বীজ মধ্যে ক্ষণস্থায়ী সত্ত্বেও প্রতিটি এক জন্য একটি ভিন্ন নমুনা উত্পাদন করা হবে, .

def f(seed, _):
  return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([ 1.2152631 ,  0.7818249 ,  0.32549605,  0.6828047 ,
                     1.3973192 , -0.57830244,  0.37862757,  2.7706041 ],                   dtype=float32)

একটি একক ডিভাইসে এই বিতরণের একটি সমতুল্য উপস্থাপনা হল মাত্র 8টি স্বাধীন স্বাভাবিক নমুনা। যদিও নমুনা মান আলাদা হতে হবে ( tfed.Sharded সিউডো-রেণ্ডম সংখ্যা প্রজন্মের সামান্য ভিন্নভাবে করে), তারা উভয় একই বন্টন প্রতিনিধিত্ব করে।

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))

DeviceArray([ 0.08086783, -0.38624594, -0.3756545 ,  1.668957  ,
             -1.2758069 ,  2.1192007 , -0.85821325,  1.1305912 ],            dtype=float32)

একটি লগ ঘনত্বের গ্রহণ Sharded বন্টন

দেখা যাক যখন আমরা একটি SPMD প্রসঙ্গে একটি নিয়মিত বিতরণ থেকে একটি নমুনার লগ-ঘনত্ব গণনা করি তখন কী ঘটে।

def f(seed, _):
  dist = tfd.Normal(0., 1.)
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                     -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32),
 ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
                     -0.94012403, -0.94012403, -0.94012403, -0.94012403],                   dtype=float32))

প্রতিটি নমুনা প্রতিটি ডিভাইসে একই, তাই আমরা প্রতিটি ডিভাইসেও একই ঘনত্ব গণনা করি। স্বজ্ঞাতভাবে, এখানে আমাদের কেবলমাত্র একটি একক সাধারণভাবে বিতরণ করা ভেরিয়েবলের উপর একটি বিতরণ রয়েছে।

একটি সঙ্গে Sharded বন্টন, আমরা তাই যখন আমরা গনা 8 র্যান্ডম ভেরিয়েবল উপর একটি বিতরণ আছে, log_prob একটি নমুনা, আমরা যোগফল, বিভিন্ন ডিভাইস জুড়ে পৃথক লগ ঘনত্বের প্রতিটি করেছে। (আপনি লক্ষ্য করতে পারেন যে এই মোট log_prob মান উপরে গণনা করা singleton log_prob থেকে বড়।)

def f(seed, _):
  dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
    random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)

Sample: [ 1.2152631   0.7818249   0.32549605  0.6828047   1.3973192  -0.57830244
  0.37862757  2.7706041 ]
Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205
 -13.7349205 -13.7349205]

সমতুল্য, "আনশার্ডেড" ডিস্ট্রিবিউশন একই লগ ঘনত্ব তৈরি করে।

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)

DeviceArray(-13.7349205, dtype=float32)

একজন Sharded বন্টন থেকে আলাদা মান উৎপন্ন sample প্রতিটি ডিভাইসে কিন্তু একই মান পেতে log_prob প্রতিটি ডিভাইসে। এখানে কি হচ্ছে? একজন Sharded বন্টন একটি করে psum নিশ্চিত করার অভ্যন্তরীণভাবে log_prob মান ডিভাইস জুড়ে সিঙ্ক হয়। কেন আমরা এই আচরণ চাই? আমরা প্রতিটি ডিভাইসে একই এমসিএমসি শৃঙ্খল চালিয়ে থাকেন, আমরা চাই target_log_prob , প্রতিটি ডিভাইস জুড়ে একই এমনকি যদি গণনার মধ্যে কিছু র্যান্ডম ভেরিয়েবল ডিভাইস জুড়ে sharded করছে।

উপরন্তু, একটি Sharded বন্টন নিশ্চিত করে যে ডিভাইস জুড়ে গ্রেডিয়েন্ট সঠিক ক্ষেত্রে HMC মতো আলগোরিদিম, যা রূপান্তর ফাংশন অংশ হিসেবে লগ-ঘনত্ব ফাংশন গ্রেডিয়েন্ট নেওয়া সঠিক নমুনা উত্পাদন নিশ্চিত করতে হবে।

Sharded JointDistribution গুলি

আমরা একাধিক মডেল তৈরি করতে পারেন Sharded ব্যবহার করে র্যান্ডম ভেরিয়েবল JointDistribution গুলি (JDS)। দুর্ভাগ্যবশত, Sharded ডিস্ট্রিবিউশন নিরাপদে সঙ্গে ভ্যানিলা ব্যবহার করা যাবে না tfd.JointDistribution গুলি কিন্তু tfp.experimental.distribute রপ্তানির "patched" JDS যে ভালো আচরণ করবে Sharded ডিস্ট্রিবিউশন।

def f(seed, _):
  dist = tfed.JointDistributionSequential([
    tfd.Normal(0., 1.),
    tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
  ])
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
                      1.6121525, 1.6121525, 1.6121525], dtype=float32),
  ShardedDeviceArray([ 0.8690128 , -0.83167845,  1.2209264 ,  0.88412696,
                       0.76478404, -0.66208494, -0.0129658 ,  0.7391483 ],                   dtype=float32)],
 ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
                     -12.214451, -12.214451, -12.214451, -12.214451],                   dtype=float32))

এই sharded JDS উভয় থাকতে পারে Sharded উপাদান হিসাবে এবং ভ্যানিলা TFP ডিস্ট্রিবিউশন। আনশার্ডড ডিস্ট্রিবিউশনের জন্য, আমরা প্রতিটি ডিভাইসে একই নমুনা পাই এবং শার্ডড ডিস্ট্রিবিউশনের জন্য আমরা বিভিন্ন নমুনা পাই। log_prob প্রতিটি ডিভাইসে পাশাপাশি সিঙ্ক্রোনাইজ করা হয়।

সঙ্গে এমসিএমসি Sharded ডিস্ট্রিবিউশন

আমরা কীভাবে মনে করেন Sharded এমসিএমসি প্রেক্ষাপটে ডিস্ট্রিবিউশন? আমরা একটি সৃজক মডেল যে হিসেবে প্রকাশ করা যেতে পারে যদি JointDistribution , আমরা জুড়ে "ঠিকরা" এ মডেলটির কিছু অক্ষ বাছাই করতে পারেন। সাধারণত, মডেলের একটি র্যান্ডম ভেরিয়েবল পর্যবেক্ষিত ডেটার সাথে মিলে যায়, এবং যদি আমাদের কাছে একটি বড় ডেটাসেট থাকে যা আমরা ডিভাইস জুড়ে শার্ড করতে চাই, আমরা চাই যে ডেটা পয়েন্টগুলির সাথে যুক্ত ভেরিয়েবলগুলিকেও শার্ড করা হোক। আমাদের "স্থানীয়" র্যান্ডম ভেরিয়েবল থাকতে পারে যেগুলি আমরা যে পর্যবেক্ষণগুলি শার্ড করছি তার সাথে এক-এক, তাই আমাদের সেই র্যান্ডম ভেরিয়েবলগুলিকে অতিরিক্তভাবে শার্ড করতে হবে।

আমরা ব্যবহার উদাহরণ উপর যাবেন Sharded এই বিভাগে TFP এমসিএমসি সঙ্গে ডিস্ট্রিবিউশন। আমরা একটি সহজ Bayesian লজিস্টিক রিগ্রেশন উদাহরণ দিয়ে শুরু, এবং একটি ম্যাট্রিক্স গুণকনির্ণয় উদাহরণ উপসংহার, কিছু ব্যবহার-মামলা প্রদর্শক জন্য লক্ষ্যে করব distribute গ্রন্থাগার।

উদাহরণ: MNIST-এর জন্য Bayesian লজিস্টিক রিগ্রেশন

আমরা একটি বড় ডেটাসেটে বায়েসিয়ান লজিস্টিক রিগ্রেশন করতে চাই; মডেল একটি পূর্বে হয়েছে \(p(\theta)\) রিগ্রেশন ওজন বেশি, এবং একটি সম্ভাবনা \(p(y_i | \theta, x_i)\) যে সব ডেটার উপর সংকলিত \(\{x_i, y_i\}_{i = 1}^N\) মোট যৌথ লগ ঘনত্ব প্রাপ্ত। আমরা আমাদের তথ্য ঠিকরা, তাহলে আমরা পর্যবেক্ষিত র্যান্ডম ভেরিয়েবল ঠিকরা চাই \(x_i\) এবং \(y_i\) আমাদের মডেল।

আমরা MNIST শ্রেণীবিভাগের জন্য নিম্নলিখিত Bayesian লজিস্টিক রিগ্রেশন মডেল ব্যবহার করি:

\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]

TensorFlow ডেটাসেট ব্যবহার করে MNIST লোড করা যাক।

mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.

raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.

Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1...
WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your
local data directory. If you'd instead prefer to read directly from our public
GCS bucket (recommended if you're running on GCP), you can instead pass
`try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`.
HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio…
Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.

আমাদের কাছে 60000টি প্রশিক্ষণের চিত্র রয়েছে তবে আসুন আমাদের 8টি উপলব্ধ কোরের সুবিধা গ্রহণ করি এবং এটিকে 8টি উপায়ে বিভক্ত করি। আমরা এই কুশলী ব্যবহার করব shard ইউটিলিটি ফাংশন।

def shard_value(x):
  x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
  return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices

shard = functools.partial(jax.tree_map, shard_value)

sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)

(8, 7500, 784) (8, 7500)

আমরা চালিয়ে যাওয়ার আগে, আসুন দ্রুত TPU-এর নির্ভুলতা এবং HMC-তে এর প্রভাব নিয়ে আলোচনা করি। TPUs কম ব্যবহার ম্যাট্রিক্স multiplications চালানো bfloat16 গতির জন্য স্পষ্টতা। bfloat16 ম্যাট্রিক্স multiplications প্রায়ই অনেক গভীর শিক্ষা অ্যাপ্লিকেশনের জন্য যথেষ্ট, কিন্তু যখন ক্ষেত্রে HMC সঙ্গে ব্যবহার, আমরা প্রায়োগিক পাওয়া যায় কম স্পষ্টতা নির্দিষ্ট আবক্র বিচ্যুত, rejections ঘটাচ্ছে হতে পারে। আমরা কিছু অতিরিক্ত গণনার খরচে উচ্চ নির্ভুলতা ম্যাট্রিক্স গুণ ব্যবহার করতে পারি।

আমাদের matmul স্পষ্টতা বৃদ্ধি করার জন্য, আমরা ব্যবহার করতে পারেন jax.default_matmul_precision সঙ্গে প্রসাধক "tensorfloat32" স্পষ্টতা (এমনকি উচ্চতর স্পষ্টতা জন্য আমরা ব্যবহার করতে পারে "float32" স্পষ্টতা)।

এখন আমাদের সংজ্ঞায়িত করা যাক run ফাংশন, যা একটি র্যান্ডম বীজ মধ্যে নিতে হবে (যা প্রতিটি ডিভাইসে একই হবে) এবং MNIST একটি ঠিকরা। ফাংশনটি পূর্বোক্ত মডেলটি বাস্তবায়ন করবে এবং তারপরে আমরা একটি একক চেইন চালানোর জন্য TFP এর ভ্যানিলা MCMC কার্যকারিতা ব্যবহার করব। আমরা নিশ্চিত সাজাইয়া করতে হবে run সঙ্গে jax.default_matmul_precision যদিও নিচে বিশেষ উদাহরণ, আমরা ঠিক যেমন ভাল ব্যবহার করতে পারে নিশ্চিত ম্যাট্রিক্স গুণ বেশী স্পষ্টতা সঙ্গে চালানো হয় করতে প্রসাধক, jnp.dot(images, w, precision=lax.Precision.HIGH)

# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device. 
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
  images, labels = data # a sharded dataset
  num_examples, dim = images.shape
  num_classes = 10

  def model_fn():
    w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
    b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
    logits = jnp.dot(images, w) + b
    yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
                       shard_axis_name='data')
  model = tfed.JointDistributionCoroutine(model_fn)

  init_seed, sample_seed = random.split(seed)

  initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`

  def target_log_prob(*state):
    return model.log_prob((*state, labels))

  def accuracy(w, b):
    logits = images.dot(w) + b
    preds = logits.argmax(axis=-1)
    # We take the average accuracy across devices by using `lax.pmean`
    return lax.pmean((preds == labels).mean(), 'data')

  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
  kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
  def trace_fn(state, pkr):
    return (
        target_log_prob(*state),
        accuracy(*state),
        pkr.new_step_size)
  states, trace = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    current_state=initial_state,
    kernel=kernel,
    trace_fn=trace_fn,
    seed=sample_seed
  )
  return states, trace

jax.pmap একটি জে আই টি JIT কম্পাইল রয়েছে তবে কম্পাইল ফাংশন প্রথম কল পর সংরক্ষিত করা হয়েছে। আমরা ডাকবো run এবং আউটপুট সংকলন ক্যাশে করার উপেক্ষা করি।

%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s
Wall time: 1min 54s

আমরা এখন ডাকবো run আবার দেখতে কতদিন প্রকৃত মৃত্যুদন্ড লাগে।

%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s
Wall time: 1min 43s

আমরা 200,000টি লিপফ্রগ ধাপ চালাচ্ছি, যার প্রতিটি সমগ্র ডেটাসেটের উপর একটি গ্রেডিয়েন্ট গণনা করে। 8টি কোরের উপর গণনা বিভক্ত করা আমাদেরকে প্রায় 95 সেকেন্ডে প্রশিক্ষণের 200,000 যুগের সমতুল্য গণনা করতে সক্ষম করে, প্রতি সেকেন্ডে প্রায় 2,100 যুগ!

আসুন প্রতিটি নমুনার লগ-ঘনত্ব এবং প্রতিটি নমুনার যথার্থতা প্লট করি:

fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()

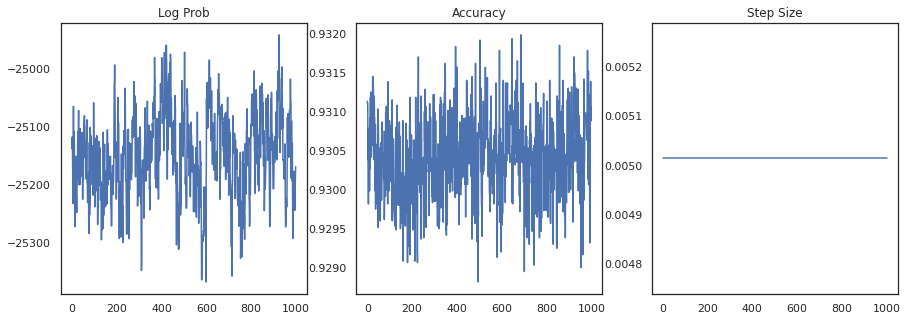
যদি আমরা নমুনাগুলি একত্রিত করি, আমরা আমাদের কর্মক্ষমতা উন্নত করতে একটি Bayesian মডেল গড় গণনা করতে পারি।

@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
  images, labels = data
  logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
  probs = jax.nn.softmax(logits, axis=-1)
  bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
  avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
  return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')

sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')

Average Accuracy: 0.9188529253005981
BMA Accuracy: 0.9264000058174133
Accuracy Improvement: 0.0075470805168151855

একটি Bayesian মডেল গড় আমাদের নির্ভুলতা প্রায় 1% বৃদ্ধি করে!

উদাহরণ: MovieLens সুপারিশ সিস্টেম

আসুন এখন মুভিলেন্সের সুপারিশ ডেটাসেটের সাথে অনুমান করার চেষ্টা করি, যা ব্যবহারকারীদের একটি সংগ্রহ এবং বিভিন্ন চলচ্চিত্রের তাদের রেটিং। বিশেষ করে, আমরা একটি হিসাবে MovieLens উপস্থাপন করতে পারেন \(N \times M\) ঘড়ি ম্যাট্রিক্স \(W\) যেখানে \(N\) ব্যবহারকারী এবং সংখ্যা \(M\) চলচ্চিত্র সংখ্যা; আমরা আশা \(N > M\)। এর এন্ট্রি \(W_{ij}\) একটি বুলিয়ান ইঙ্গিত থাকুক বা না থাকুক ব্যবহারকারী হন \(i\) প্রেক্ষিত সিনেমা \(j\)। মনে রাখবেন যে MovieLens ব্যবহারকারীর রেটিং প্রদান করে, কিন্তু আমরা সমস্যাটিকে সহজ করার জন্য সেগুলিকে উপেক্ষা করছি৷

প্রথমে, আমরা ডেটাসেট লোড করব। আমরা 1 মিলিয়ন রেটিং সহ সংস্করণটি ব্যবহার করব।

movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
          'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
          'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
          'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']

Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0...
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl…

HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value='')))
Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord
HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value='')))
Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.

আমরা ঘড়ি ম্যাট্রিক্স প্রাপ্ত ডেটাসেটের কিছু প্রাক-প্রক্রিয়াকরণ করব \(W\)।

raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']

movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])

num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1

movie_titles = dict(zip(movielens['train']['movie_id'],
                        movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
                        genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
                     for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]

watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)

(6040, 3706)

আমরা একটি সৃজক মডেল বর্ণনা করতে পারেন \(W\), একটি সহজ সম্ভাব্য ম্যাট্রিক্স গুণকনির্ণয় মডেল ব্যবহার করে। আমরা একটি সুপ্ত অনুমান \(N \times D\) ব্যবহারকারী ম্যাট্রিক্স \(U\) এবং একটি সুপ্ত \(M \times D\) সিনেমা ম্যাট্রিক্স \(V\), যা যখন গুন ঘড়ি ম্যাট্রিক্স একটি বের্নুলির logits উত্পাদন \(W\)। আমরা ব্যবহারকারী এবং চলচ্চিত্র, একটি পক্ষপাত ভেক্টর অন্তর্ভুক্ত করব \(u\) এবং \(v\)।

\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]

এটি একটি চমত্কার বড় ম্যাট্রিক্স; 6040 ব্যবহারকারী এবং 3706টি চলচ্চিত্র 22 মিলিয়নেরও বেশি এন্ট্রি সহ একটি ম্যাট্রিক্সের দিকে নিয়ে যায়। কিভাবে আমরা এই মডেল sharding যোগাযোগ করব? ওয়েল, যদি আমরা ধরে নিই যে \(N > M\) (সিনেমা বেশি ব্যবহারকারীর আছে অর্থাত), তারপর এটা জানার জন্য হবে ব্যবহারকারী অক্ষ জুড়ে ঘড়ি ম্যাট্রিক্স ঠিকরা, তাই প্রতিটি ডিভাইস ব্যবহারকারীদের একটি উপসেট সংশ্লিষ্ট ঘড়ি ম্যাট্রিক্স একটি খণ্ড হবে . পূর্ববর্তী উদাহরণ থেকে পৃথক, কিন্তু, আমরা আপ ঠিকরা করতে হবে \(U\) ম্যাট্রিক্স, যেহেতু এটি প্রত্যেক ব্যবহারকারীর জন্য একটি এম্বেড আছে, তাই প্রতিটি যন্ত্রের একটি ঠিকরা জন্য দায়ী করা হবে \(U\) এবং একটি ঠিকরা \(W\). অন্যদিকে, \(V\) unsharded হতে পারে এবং ডিভাইস জুড়ে সিঙ্ক্রোনাইজ করা।

sharded_watch_matrix = shard(watch_matrix)

আগে আমাদের লিখতে run , এর দ্রুত স্থানীয় দৈব চলক sharding অতিরিক্ত চ্যালেঞ্জ আলোচনা করি \(U\)। যখন ক্ষেত্রে HMC, ভ্যানিলা চলমান tfp.mcmc.HamiltonianMonteCarlo কার্নেল নমুনা হবে শৃঙ্খল রাষ্ট্রীয় প্রতিটি উপাদানের জন্য momenta। পূর্বে, শুধুমাত্র unsharded র্যান্ডম ভেরিয়েবলগুলি সেই অবস্থার অংশ ছিল এবং প্রতিটি ডিভাইসে মোমেন্টা একই ছিল। আমরা এখন একটি sharded আছে \(U\), আমরা একে ডিভাইসে বিভিন্ন momenta নমুনা প্রয়োজন \(U\)জন্য একই momenta স্যাম্পলিং সময় \(V\)। এই কাজ করা সম্ভব করতে, আমরা ব্যবহার করতে পারেন tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo একটি সঙ্গে Sharded ভরবেগ বন্টন। যেহেতু আমরা সমান্তরাল গণনা প্রথম-শ্রেণীর করা চালিয়ে যাচ্ছি, আমরা এটিকে সরল করতে পারি, যেমন HMC কার্নেলে একটি শার্ডিনেস ইন্ডিকেটর নিয়ে।

def make_run(*,
             axis_name,
             dim=20,
             num_chains=2,
             prior_variance=1.,
             step_size=1e-2,
             num_leapfrog_steps=100,
             num_burnin_steps=1000,
             num_results=500,
             ):
  @functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
  @jax.default_matmul_precision('tensorfloat32')
  def run(key, watch_matrix):
    num_users, num_movies = watch_matrix.shape

    Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)

    def prior_fn():
      user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
      user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
      movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
      movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
      return (user_embeddings, user_bias, movie_embeddings, movie_bias)
    prior = tfed.JointDistributionCoroutine(prior_fn)

    def model_fn():
      user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
      logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
                + user_bias[..., :, None] + movie_bias[..., None, :])
      yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
    model = tfed.JointDistributionCoroutine(model_fn)

    init_key, sample_key = random.split(key)
    initial_state = prior.sample(seed=init_key, sample_shape=num_chains)

    def target_log_prob(*state):
      return model.log_prob((*state, watch_matrix))

    momentum_distribution = tfed.JointDistributionSequential([
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
    ])

    # We pass in momentum_distribution here to ensure that the momenta for 
    # user_embeddings and user_bias are also sharded
    kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
                                                      num_leapfrog_steps,
                                                      momentum_distribution=momentum_distribution)

    num_adaptation_steps = int(0.8 * num_burnin_steps)
    kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)

    def trace_fn(state, pkr):
      return {
        'log_prob': target_log_prob(*state),
        'log_accept_ratio': pkr.inner_results.log_accept_ratio,
      }
    return tfm.sample_chain(
        num_results, initial_state,
        kernel=kernel,
        num_burnin_steps=num_burnin_steps,
        trace_fn=trace_fn,
        seed=sample_key)
  return run

সংকলিত ক্যাশে একবার আমরা আবার এটিকে চালাতে পারবেন run ।

%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 56 s, sys: 1min 24s, total: 2min 20s
Wall time: 3min 35s

এখন আমরা কম্পাইলেশন ওভারহেড ছাড়াই এটি আবার চালাব।

%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s
Wall time: 3min 1s

দেখে মনে হচ্ছে আমরা প্রায় 3 মিনিটে প্রায় 150,000টি লিপফ্রগ ধাপ সম্পূর্ণ করেছি, তাই প্রতি সেকেন্ডে প্রায় 83টি লিপফ্রগ ধাপ! আসুন আমাদের নমুনার গ্রহণ অনুপাত এবং লগ ঘনত্ব প্লট করা যাক।

fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
  ax.plot(val[0]) # Indexing into a sharded array, each element is the same
  ax.set_title(key);

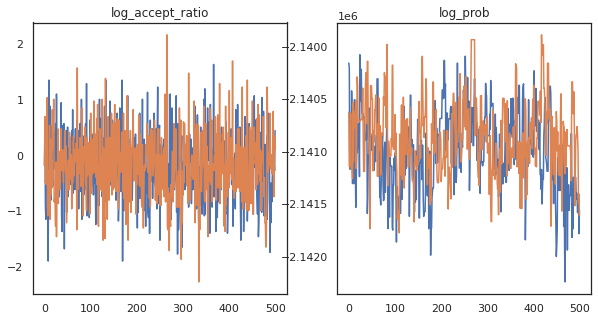
এখন যেহেতু আমাদের মার্কভ চেইন থেকে কিছু নমুনা আছে, আসুন কিছু ভবিষ্যদ্বাণী করতে সেগুলি ব্যবহার করি। প্রথমে, আসুন প্রতিটি উপাদান বের করি। মনে রাখবেন যে user_embeddings এবং user_bias , ডিভাইসের জুড়ে বিভক্ত, তাই আমরা আমাদের কনক্যাটেনেট প্রয়োজন ShardedArray তাদের সবাইকে প্রাপ্ত। অন্যদিকে, movie_embeddings এবং movie_bias প্রত্যেকটি ডিভাইসে একই, তাই আমরা শুধুমাত্র প্রথম ঠিকরা থেকে মান বাছাই করতে পারেন। আমরা নিয়মিত ব্যবহার করব numpy CPU- র TPUs পিছন থেকে মান কপি করার।

user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')

User embeddings: (500, 2, 6040, 20)
User bias: (500, 2, 6040)
Movie embeddings: (500, 2, 3706, 20)
Movie bias: (500, 2, 3706)

আসুন একটি সাধারণ সুপারিশকারী সিস্টেম তৈরি করার চেষ্টা করি যা এই নমুনাগুলিতে ক্যাপচার করা অনিশ্চয়তাকে কাজে লাগায়। চলুন প্রথমে একটি ফাংশন লিখি যা মুভিগুলিকে ঘড়ির সম্ভাব্যতা অনুসারে স্থান দেয়।

@jax.jit
def recommend(sample, user_id):
  user_embeddings, user_bias, movie_embeddings, movie_bias = sample
  movie_logits = (
      jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
      + user_bias[user_id] + movie_bias)
  return movie_logits.argsort()[::-1]

আমরা এখন এমন একটি ফাংশন লিখতে পারি যা সমস্ত নমুনাকে লুপ করে এবং প্রতিটির জন্য, শীর্ষস্থানীয় মুভি বাছাই করে যা ব্যবহারকারী ইতিমধ্যে দেখেনি। তারপরে আমরা সমস্ত নমুনা জুড়ে প্রস্তাবিত সিনেমাগুলির গণনা দেখতে পারি।

def get_recommendations(user_id): 
  movie_ids = []
  already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
  for i in range(500):
    for j in range(2):
      sample = jax.tree_map(lambda x: x[i, j], samples)
      ranking = recommend(sample, user_id)
      for movie_id in ranking:
        if int(movie_id) not in already_watched:
          movie_ids.append(movie_id)
          break
  return movie_ids

def plot_recommendations(movie_ids, ax=None):
  titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
  ax = ax or plt.gca()
  names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
  ax.bar(names, counts)
  ax.set_xticklabels(names, rotation=90)

সবচেয়ে বেশি মুভি দেখেছেন এমন ব্যবহারকারীর বিপরীতে যিনি সবচেয়ে কম দেখেছেন তাকেই ধরা যাক।

user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])

2314 20

আমাদের সিস্টেমে সম্পর্কে আরো নিশ্চয়তা রয়েছে আশা করি user_most চেয়ে user_least দেওয়া কি আমরা সিনেমা প্রকারের সম্পর্কে আরও তথ্য আছে যে user_most আরও অনেক কিছু দেখুন পারে।

fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');

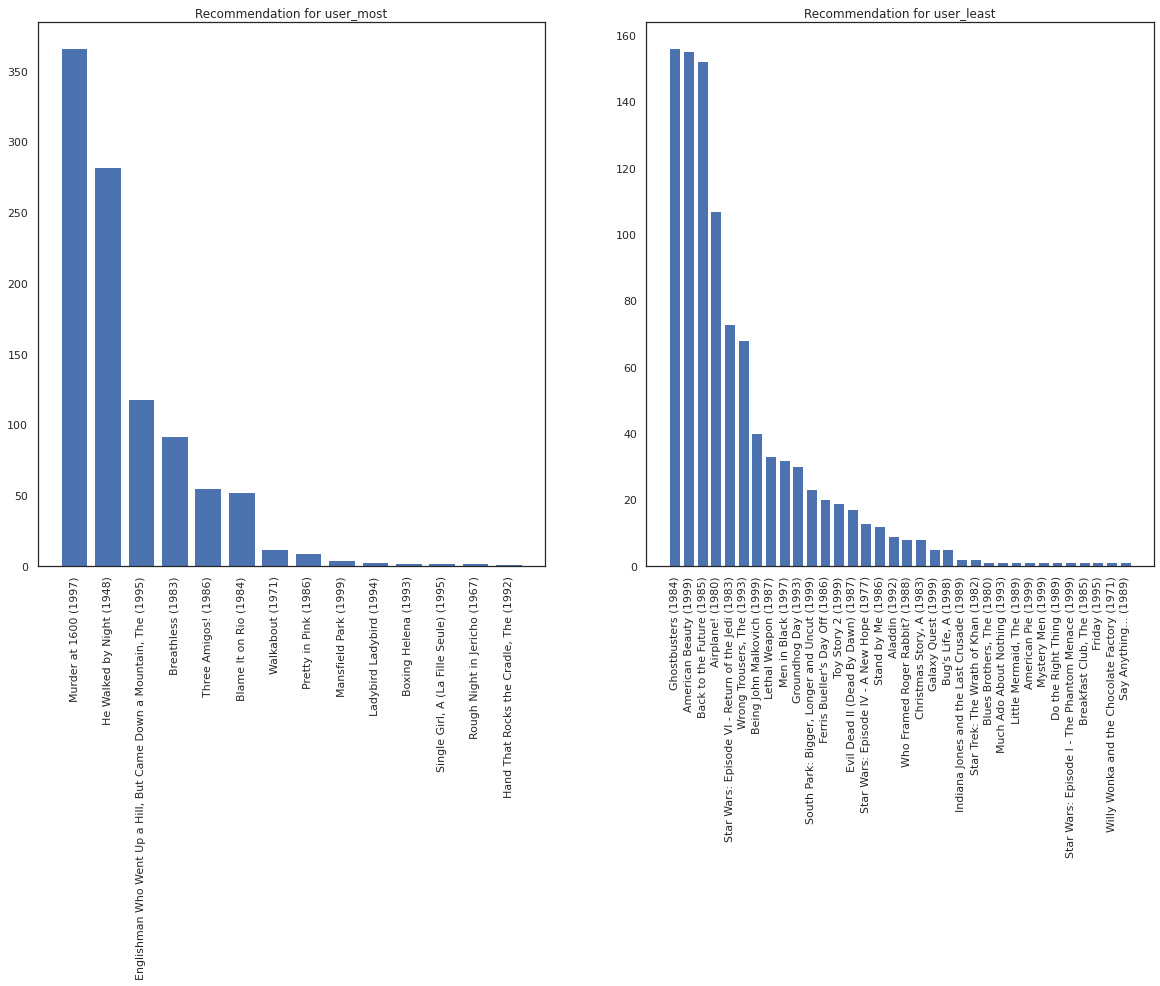
আমরা আমাদের সুপারিশ আরও ভ্যারিয়েন্স আছে দেখতে user_least তাদের ঘড়ি পছন্দগুলি আমাদের অতিরিক্ত অনিশ্চয়তা অনুধ্যায়ী।

আমরা প্রস্তাবিত সিনেমার ধরণগুলিও দেখতে পারি।

most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');

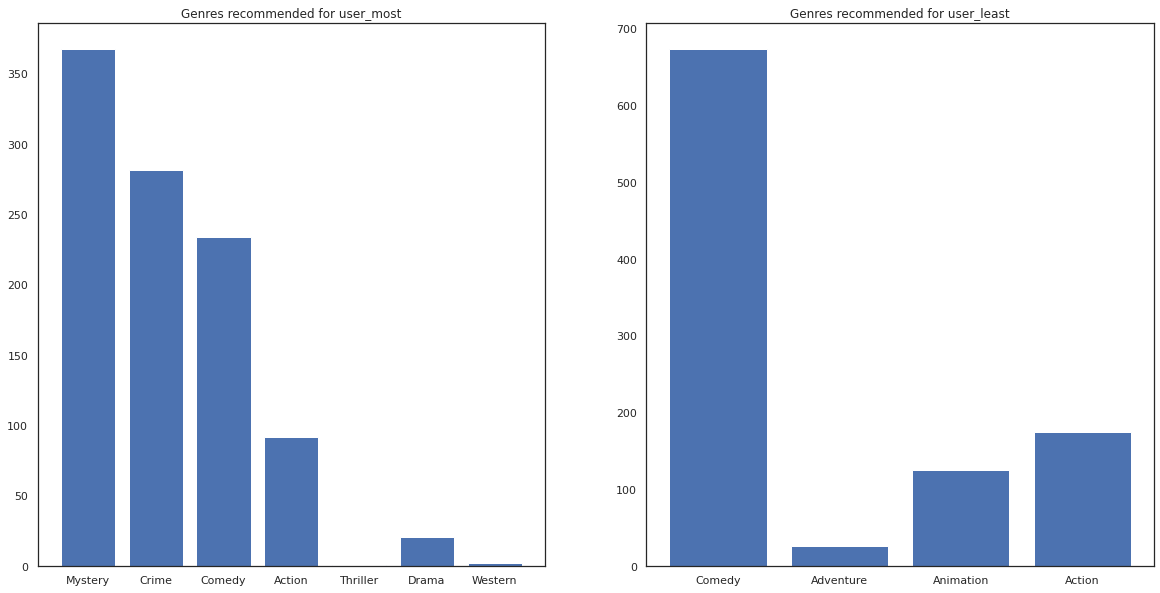
user_most সিনেমা অনেক দেখেছেন আর রহস্য অপরাধ মত আরো কুলুঙ্গি ঘরানার সুপারিশ করা হয়েছে যেহেতু user_least অনেক চলচ্চিত্র প্রেক্ষিত নি এবং আরো মূলধারার চলচ্চিত্র, যা স্কিউ কমেডি এবং ব্যবস্থা নেয়ার সুপারিশ করা হয়েছে।