عرض على TensorFlow.org

تشغيل في Google Colab

عرض المصدر على جيثب

تحميل دفتر

لدى TensorFlow Probability (TFP) على JAX الآن أدوات للحوسبة الرقمية الموزعة. للتوسع في أعداد كبيرة من المسرّعات ، تم بناء الأدوات حول كتابة التعليمات البرمجية باستخدام نموذج "برنامج واحد متعدد البيانات" ، أو اختصارًا SPMD.

في هذا الكمبيوتر الدفتري ، سنتعرف على كيفية "التفكير في SPMD" ونقدم تجريدات TFP الجديدة لتوسيع نطاق التكوينات مثل كبسولات TPU أو مجموعات وحدات معالجة الرسومات. إذا كنت تقوم بتشغيل هذا الرمز بنفسك ، فتأكد من تحديد وقت تشغيل TPU.

سنقوم أولاً بتثبيت أحدث إصدارات TFP و JAX و TF.

التثبيتات

pip install jaxlib --upgrade -q 2>&1 1> /dev/null
pip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/null
pip install tf-nightly-cpu -q -I 2>&1 1> /dev/null
pip install jax -I -q --upgrade 2>&1 1>/dev/null

سنقوم باستيراد بعض المكتبات العامة ، جنبًا إلى جنب مع بعض أدوات JAX المساعدة.

الإعداد والواردات

import functools
import collections
import contextlib

import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds

from tensorflow_probability.substrates import jax as tfp

sns.set(style='white')

INFO:tensorflow:Enabling eager execution
INFO:tensorflow:Enabling v2 tensorshape
INFO:tensorflow:Enabling resource variables
INFO:tensorflow:Enabling tensor equality
INFO:tensorflow:Enabling control flow v2

سنقوم أيضًا بإعداد بعض الأسماء المستعارة لـ TFP. يتم توفير تجريدية جديدة حاليا في tfp.experimental.distribute و tfp.experimental.mcmc .

tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc

Root = tfed.JointDistributionCoroutine.Root

لتوصيل الكمبيوتر الدفتري بجهاز TPU ، نستخدم المساعد التالي من JAX. للتأكد من أننا متصلون ، نطبع عدد الأجهزة ، الذي يجب أن يكون ثمانية.

from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')

Found 8 devices

مقدمة سريعة ل jax.pmap

بعد الاتصال إلى TPU، لدينا إمكانية الوصول إلى ثمانية أجهزة. ومع ذلك ، عندما نقوم بتشغيل كود JAX بفارغ الصبر ، فإن JAX تكون افتراضية لتشغيل العمليات الحسابية على واحد فقط.

إن أبسط طريقة لتنفيذ عملية حسابية عبر العديد من الأجهزة هي تعيين وظيفة ، بحيث يقوم كل جهاز بتنفيذ فهرس واحد على الخريطة. يوفر JAX في jax.pmap ( "خارطة الموازية") تحول الأمر الذي يجعل وظيفة في واحدة التي تعين على وظيفة عبر العديد من الأجهزة.

في المثال التالي ، قمنا بإنشاء مصفوفة بحجم 8 (لمطابقة عدد الأجهزة المتاحة) وقمنا بتعيين وظيفة تضيف 5 عبرها.

xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)

<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5.  6.  7.  8.  9. 10. 11. 12.]

علما بأن نتلقى ShardedDeviceArray نوع الظهر، مشيرا إلى أن مجموعة الانتاج يتم تقسيم جسديا عبر الأجهزة.

jax.pmap يعمل غويا مثل الخريطة، ولكن لديها عدد قليل من الخيارات الهامة التي تعدل سلوكها. افتراضيا، pmap يفترض يتم تعيين جميع المدخلات إلى وظيفة أكثر، ولكن يمكننا تعديل هذا السلوك مع in_axes حجة.

xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)

[ 5.  6.  7.  8.  9. 10. 11. 12.]

بالقياس، و out_axes حجة ل pmap يحدد ما إذا كان أو لم يكن لإرجاع القيم على كل جهاز. وضع out_axes ل None تلقائيا بإرجاع قيمة على الجهاز 1st و ينبغي ألا تستخدم إلا إذا كنا على ثقة من القيم هي نفسها على كل جهاز.

xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)

2.0

ماذا يحدث عندما لا يمكن التعبير عن ما نرغب في القيام به بسهولة كدالة نقية معينة؟ على سبيل المثال ، ماذا لو أردنا إجراء مجموع عبر المحور الذي نرسمه؟ تقدم JAX "مجموعات" ، وهي وظائف تتواصل عبر الأجهزة ، لتمكين كتابة برامج موزعة أكثر تشويقًا وتعقيدًا. لفهم كيفية عملها بالضبط ، سنقدم SPMD.

ما هو SPMD؟

البيانات المتعددة أحادية البرنامج (SPMD) هي نموذج برمجة متزامن يتم فيه تنفيذ برنامج واحد (أي نفس الرمز) في وقت واحد عبر الأجهزة ، ولكن يمكن أن تختلف مدخلات كل برنامج من البرامج قيد التشغيل.

إذا برنامجنا هو وظيفة بسيطة من مدخلاته (أي شيء من هذا القبيل x + 5 )، تشغيل برنامج في SPMD هو مجرد رسم ذلك البيانات المختلفة أكثر، كما فعلنا مع jax.pmap في وقت سابق. ومع ذلك ، يمكننا أن نفعل أكثر من مجرد "تعيين" وظيفة. تقدم JAX "المجموعات" ، وهي وظائف تتواصل عبر الأجهزة.

على سبيل المثال ، ربما نرغب في أخذ مجموع الكمية عبر جميع أجهزتنا. قبل ان نفعل ذلك، نحن بحاجة لتعيين اسم لمحور نحن الخرائط كنت فوق في pmap . نحن ثم استخدم lax.psum وظيفة ( "مبلغ مواز") لتنفيذ المبلغ عبر الأجهزة، وضمان نحدد اسمه محور نحن تلخيص أكثر.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)

ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)

و psum المجاميع الجماعية قيمة x على كل جهاز ومزامنة قيمته عبر الخريطة، أي out هو 28. على كل جهاز. لم نعد نقوم بتنفيذ "خريطة" بسيطة ، لكننا ننفذ برنامج SPMD حيث يمكن الآن لحسابات كل جهاز أن تتفاعل مع نفس الحساب على الأجهزة الأخرى ، وإن كان ذلك بطريقة محدودة باستخدام المجموعات. في هذا السيناريو، يمكننا استخدام out_axes = None ، لأن psum سوف مزامنة القيمة.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))

ShardedDeviceArray(28., dtype=float32)

يتيح لنا SPMD كتابة برنامج واحد يتم تشغيله على كل جهاز في أي تكوين TPU في وقت واحد. يمكن استخدام نفس الكود المستخدم في التعلم الآلي على 8 نوى من مادة TPU على جراب TPU الذي قد يحتوي على مئات إلى آلاف النوى! لتعليمي أكثر تفصيلا حول jax.pmap وSPMD، يمكنك الرجوع إلى و JAX 101 التعليمي .

MCMC على نطاق واسع

في هذا الكمبيوتر الدفتري ، نركز على استخدام أساليب Markov Chain Monte Carlo (MCMC) للاستدلال البايزي. قد تكون هناك طرق لاستخدام العديد من الأجهزة في MCMC ، ولكن في هذا الكمبيوتر الدفتري ، سنركز على اثنين:

1. تشغيل سلاسل ماركوف المستقلة على أجهزة مختلفة. هذه الحالة بسيطة إلى حد ما ويمكن القيام بها باستخدام Vanilla TFP.
2. مشاركة مجموعة بيانات عبر الأجهزة. هذه الحالة أكثر تعقيدًا قليلاً وتتطلب آلات TFP المضافة حديثًا.

سلاسل مستقلة

لنفترض أننا نرغب في إجراء استنتاج بايزي بشأن مشكلة باستخدام MCMC ونود تشغيل عدة سلاسل بالتوازي عبر عدة أجهزة (لنقل 2 على كل جهاز). تبين أن هذا برنامج يمكننا فقط "تعيينه" عبر الأجهزة ، أي برنامج لا يحتاج إلى مجموعات. للتأكد من أن كل برنامج ينفذ سلسلة Markov مختلفة (بدلاً من تشغيل نفس السلسلة) ، نقوم بتمرير قيمة مختلفة للبذور العشوائية لكل جهاز.

لنجربها في مشكلة لعبة لأخذ عينات من توزيع غاوسي ثنائي الأبعاد. يمكننا استخدام وظيفة MCMC الحالية الخاصة بـ TFP من خارج الصندوق. بشكل عام ، نحاول وضع معظم المنطق داخل الوظيفة المعينة لدينا للتمييز بشكل أكثر وضوحًا بين ما يتم تشغيله على جميع الأجهزة مقابل الأول فقط.

def run(seed):
  target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob

  initial_state = jnp.zeros([2, 2]) # 2 chains
  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
  def trace_fn(state, pkr):
    return target_log_prob(state)

  states, log_prob = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    kernel=kernel,
    current_state=initial_state,
    trace_fn=trace_fn,
    seed=seed
  )
  return states, log_prob

في حد ذاته، و run يأخذ وظيفة في البذور عشوائي عديمي الجنسية (البدون لنرى كيف العمل العشوائية، يمكنك قراءة TFP على JAX المحمول أو رؤية البرنامج التعليمي JAX 101 ). خرائط run وأكثر من البذور المختلفة يؤدي إلى تشغيل عدة سلاسل ماركوف مستقلة.

states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)

(8, 1000, 2, 2) (8, 1000, 2)

لاحظ كيف لدينا الآن محور إضافي يتوافق مع كل جهاز. يمكننا إعادة ترتيب الأبعاد وتسويتها للحصول على محور لـ 16 سلسلة.

states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])

fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()

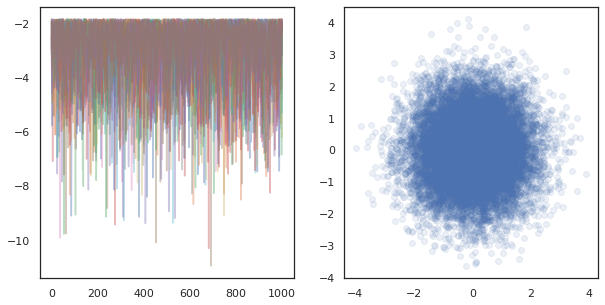
عند تشغيل سلاسل المستقلة على العديد من الأجهزة، انها سهلة كما pmap -ing على وظيفة أن الاستخدامات tfp.mcmc ، وضمان نجتاز قيم مختلفة للالبذور عشوائي لكل جهاز.

تقاسم البيانات

عندما نقوم بعمل MCMC ، غالبًا ما يكون التوزيع المستهدف هو التوزيع اللاحق الذي يتم الحصول عليه عن طريق التكييف على مجموعة بيانات ، ويتضمن حساب كثافة السجل غير الطبيعية جمع الاحتمالات لكل بيانات تمت ملاحظتها.

مع مجموعات البيانات الكبيرة جدًا ، قد يكون تشغيل سلسلة واحدة على جهاز واحد مكلفًا للغاية. ومع ذلك ، عندما نتمكن من الوصول إلى أجهزة متعددة ، يمكننا تقسيم مجموعة البيانات عبر الأجهزة للاستفادة بشكل أفضل من الحوسبة المتوفرة لدينا.

إذا كنا نرغب في القيام MCMC مع مجموعة بيانات sharded، نحن بحاجة إلى ضمان unnormalized سجل الكثافة نحسب على كل جهاز يمثل المجموع، أي كثافة على جميع البيانات، وإلا كل جهاز سوف تفعل MCMC مع الهدف غير صحيح الخاصة توزيع. ولهذه الغاية، TFP لديها الآن أدوات جديدة (أي tfp.experimental.distribute و tfp.experimental.mcmc ) التي تمكن الحوسبة "sharded" الاحتمالات سجل والقيام MCMC معهم.

توزيعات مُقسمة

يوفر التجريد TFP الأساسية الآن لحساب probabiliities سجل sharded هو Sharded الفوقية التوزيع، والتي تأخذ توزيع كمدخل وإرجاع توزيع جديد له خصائص معينة عند تنفيذها في سياق SPMD. Sharded حياة في tfp.experimental.distribute .

حدسي، و Sharded يتوافق توزيعها على مجموعة من المتغيرات العشوائية التي تم "تقسيم" عبر الأجهزة. على كل جهاز ، سينتجون عينات مختلفة ، ويمكن أن يكون لكل منهم كثافات لوغاريتمية مختلفة. بدلا من ذلك، Sharded يتوافق توزيع إلى "لوحة" في لغة نموذج الرسومية، حيث حجم لوحة هو عدد من الأجهزة.

أخذ عينات من Sharded التوزيع

إذا كان لنا عينة من Normal التوزيع في برنامج كائن pmap افتتاحية باستخدام نفس البذور على كل جهاز، سوف نحصل على نفس العينة على كل جهاز. يمكننا التفكير في الوظيفة التالية كأخذ عينات لمتغير عشوائي واحد تتم مزامنته عبر الأجهزة.

# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
  return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                    -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32)

إذا كنا التفاف tfd.Normal(0., 1.) مع tfed.Sharded ، فإننا منطقيا لديها الآن ثمانية المتغيرات العشوائية المختلفة (واحد على كل جهاز)، وبالتالي سوف تنتج عينة مختلفة لكل واحد، على الرغم من يمر في نفس البذور .

def f(seed, _):
  return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([ 1.2152631 ,  0.7818249 ,  0.32549605,  0.6828047 ,
                     1.3973192 , -0.57830244,  0.37862757,  2.7706041 ],                   dtype=float32)

تمثيل مكافئ لهذا التوزيع على جهاز واحد هو مجرد 8 عينات عادية مستقلة. على الرغم من أن قيمة العينة ستكون مختلفة ( tfed.Sharded يفعل شبه عشوائي توليد عدد مختلف قليلا)، وكلاهما يمثل نفس التوزيع.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))

DeviceArray([ 0.08086783, -0.38624594, -0.3756545 ,  1.668957  ,
             -1.2758069 ,  2.1192007 , -0.85821325,  1.1305912 ],            dtype=float32)

أخذ سجل الكثافة من Sharded التوزيع

دعونا نرى ما يحدث عندما نحسب كثافة اللوغاريتمات لعينة من توزيع منتظم في سياق SPMD.

def f(seed, _):
  dist = tfd.Normal(0., 1.)
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                     -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32),
 ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
                     -0.94012403, -0.94012403, -0.94012403, -0.94012403],                   dtype=float32))

كل عينة هي نفسها على كل جهاز ، لذلك نحسب نفس الكثافة على كل جهاز أيضًا. بشكل بديهي ، لدينا هنا فقط توزيع على متغير واحد يتم توزيعه بشكل طبيعي.

مع Sharded التوزيع، لدينا توزيع أكثر من 8 المتغيرات العشوائية، لذلك عندما كنا حساب log_prob لعينة، ونحن خلاصة القول، عبر الأجهزة، على كل من الكثافة سجل الفردية. (قد تلاحظ أن إجمالي قيمة log_prob هذه أكبر من قيمة log_prob المفرد المحسوبة أعلاه.)

def f(seed, _):
  dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
    random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)

Sample: [ 1.2152631   0.7818249   0.32549605  0.6828047   1.3973192  -0.57830244
  0.37862757  2.7706041 ]
Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205
 -13.7349205 -13.7349205]

ينتج التوزيع المكافئ "غير المقوى" نفس كثافة اللوغاريتمات.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)

DeviceArray(-13.7349205, dtype=float32)

A Sharded توزيع ينتج قيم مختلفة من sample على كل جهاز، ولكن الحصول على نفس القيمة ل log_prob على كل جهاز. ماذا يحصل هنا؟ A Sharded توزيع يقوم psum داخليا لضمان log_prob القيم متزامنة عبر الأجهزة. لماذا نريد هذا السلوك؟ إذا كان لنا أن تقوم بتشغيل نفس السلسلة MCMC على كل جهاز، نود أن target_log_prob أن تكون هي نفسها في كل جهاز، حتى لو تم sharded بعض المتغيرات العشوائية في حساب عبر الأجهزة.

بالإضافة إلى ذلك، Sharded يضمن التوزيع التي التدرجات عبر الأجهزة هي صحيحة، لضمان أن خوارزميات مثل مؤسسة حمد الطبية، والتي تأخذ التدرجات وظيفة سجل الكثافة كجزء من وظيفة التحول، وإنتاج العينات المناسبة.

Sharded JointDistribution الصورة

يمكننا خلق نماذج متعددة مع Sharded المتغيرات العشوائية باستخدام JointDistribution الصورة (دينار). للأسف، Sharded توزيعات لا يمكن استخدامها بأمان مع الفانيليا tfd.JointDistribution الصورة، ولكن tfp.experimental.distribute الصادرات "يرقع" دينار التي سوف تتصرف مثل Sharded التوزيعات.

def f(seed, _):
  dist = tfed.JointDistributionSequential([
    tfd.Normal(0., 1.),
    tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
  ])
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
                      1.6121525, 1.6121525, 1.6121525], dtype=float32),
  ShardedDeviceArray([ 0.8690128 , -0.83167845,  1.2209264 ,  0.88412696,
                       0.76478404, -0.66208494, -0.0129658 ,  0.7391483 ],                   dtype=float32)],
 ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
                     -12.214451, -12.214451, -12.214451, -12.214451],                   dtype=float32))

ويمكن لهذه دينار sharded على حد سواء Sharded والفانيليا TFP توزيعات كمكونات. بالنسبة للتوزيعات غير المجهزة ، نحصل على نفس العينة على كل جهاز ، وبالنسبة للتوزيعات المُقسمة ، نحصل على عينات مختلفة. و log_prob تتم مزامنة على كل جهاز أيضا.

MCMC مع Sharded التوزيعات

كيف نفكر Sharded التوزيعات في سياق MCMC؟ إذا كان لدينا نموذج توليدي التي يمكن أن يعبر عنه JointDistribution ، يمكننا اختيار بعض محور هذا النموذج ب "قشرة" عبر. عادةً ، سيتوافق أحد المتغيرات العشوائية في النموذج مع البيانات المرصودة ، وإذا كانت لدينا مجموعة بيانات كبيرة نرغب في تجزئتها عبر الأجهزة ، فنحن نريد أيضًا تجزئة المتغيرات المرتبطة بنقاط البيانات. قد يكون لدينا أيضًا متغيرات عشوائية "محلية" تكون فردية مع الملاحظات التي نقوم بتقسيمها ، لذلك سيتعين علينا إضافة هذه المتغيرات العشوائية إلى أجزاء أخرى.

سنذهب على أمثلة على استخدام Sharded توزيعات مع TFP MCMC في هذا القسم. سنبدأ مع أبسط النظرية الافتراضية سبيل المثال الانحدار اللوجستي، وتختتم مع مثال مصفوفة التعميل، وذلك بهدف إثبات بعض حالات الاستخدام ل distribute مكتبة.

مثال: الانحدار اللوجستي Bayesian لـ MNIST

نود إجراء الانحدار اللوجستي Bayesian على مجموعة بيانات كبيرة ؛ نموذج لديه مسبق \(p(\theta)\) على أوزان الانحدار، واحتمال \(p(y_i | \theta, x_i)\) التي تتلخص على جميع البيانات \(\{x_i, y_i\}_{i = 1}^N\) للحصول على مجموع كثافة السجل المشترك. إذا كنا شارد بياناتنا، كنا شارد المتغيرات العشوائية المرصودة \(x_i\) و \(y_i\) في نموذجنا.

نستخدم نموذج الانحدار اللوجستي Bayesian التالي لتصنيف MNIST:

\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]

لنقم بتحميل MNIST باستخدام مجموعات بيانات TensorFlow.

mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.

raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.

Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1...
WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your
local data directory. If you'd instead prefer to read directly from our public
GCS bucket (recommended if you're running on GCP), you can instead pass
`try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`.
HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio…
Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.

لدينا 60000 صورة تدريبية ولكن دعونا نستفيد من 8 مراكز متوفرة لدينا ونقسمها 8 طرق. سنستخدم هذا يدوية shard دالة المنفعة.

def shard_value(x):
  x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
  return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices

shard = functools.partial(jax.tree_map, shard_value)

sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)

(8, 7500, 784) (8, 7500)

قبل أن نواصل ، دعنا نناقش بسرعة الدقة على TPU وتأثيرها على HMC. TPUs تنفيذ ضرب المصفوفات باستخدام منخفضة bfloat16 الدقة للسرعة. bfloat16 ضرب المصفوفات وغالبا ما تكون كافية لكثير من تطبيقات التعلم عميقة، ولكن عندما تستخدم مع مؤسسة حمد الطبية، وجدنا تجريبيا دقة أقل يمكن أن يؤدي إلى تباين المسارات، مما تسبب في الرفض. يمكننا استخدام مضاعفات المصفوفات بدقة أعلى على حساب بعض الحسابات الإضافية.

لزيادة الدقة لدينا matmul، يمكننا استخدام jax.default_matmul_precision الديكور مع "tensorfloat32" الدقة (لأعلى دقة يمكن أن نستخدمها "float32" الدقة).

دعونا الآن تحديد لدينا run وظيفة، والتي سوف تأخذ في البذور العشوائي (والتي سوف تكون هي نفسها في كل جهاز) وكسرة فخارية من MNIST. ستقوم الوظيفة بتنفيذ النموذج المذكور أعلاه وسنستخدم بعد ذلك وظيفة Vanilla MCMC في TFP لتشغيل سلسلة واحدة. ونحن سوف نتأكد من أن تزيين run مع jax.default_matmul_precision الديكور للتأكد من تشغيل الضرب مصفوفة بدقة أعلى، وإن كان في مثال معين أدناه، فإننا يمكن أن تستخدم فقط كذلك jnp.dot(images, w, precision=lax.Precision.HIGH) .

# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device. 
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
  images, labels = data # a sharded dataset
  num_examples, dim = images.shape
  num_classes = 10

  def model_fn():
    w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
    b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
    logits = jnp.dot(images, w) + b
    yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
                       shard_axis_name='data')
  model = tfed.JointDistributionCoroutine(model_fn)

  init_seed, sample_seed = random.split(seed)

  initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`

  def target_log_prob(*state):
    return model.log_prob((*state, labels))

  def accuracy(w, b):
    logits = images.dot(w) + b
    preds = logits.argmax(axis=-1)
    # We take the average accuracy across devices by using `lax.pmean`
    return lax.pmean((preds == labels).mean(), 'data')

  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
  kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
  def trace_fn(state, pkr):
    return (
        target_log_prob(*state),
        accuracy(*state),
        pkr.new_step_size)
  states, trace = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    current_state=initial_state,
    kernel=kernel,
    trace_fn=trace_fn,
    seed=sample_seed
  )
  return states, trace

jax.pmap يتضمن ترجمة JIT ولكن تم تخزينها مؤقتا وظيفة جمعت بعد المكالمة الأولى. وسوف ندعو run وتجاهل الإخراج إلى ذاكرة التخزين المؤقت تجميع.

%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s
Wall time: 1min 54s

سنقوم الآن الدعوة run مرة أخرى لنرى كم من الوقت يستغرق التنفيذ الفعلي.

%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s
Wall time: 1min 43s

نحن ننفذ 200000 خطوة قفزة ، كل منها يحسب تدرجًا على مجموعة البيانات بأكملها. يتيح لنا تقسيم الحساب على 8 مراكز حساب ما يعادل 200000 حقبة تدريب في حوالي 95 ثانية ، أي حوالي 2100 حقبة في الثانية!

دعنا نرسم كثافة اللوغاريتمات لكل عينة ودقة كل عينة:

fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()

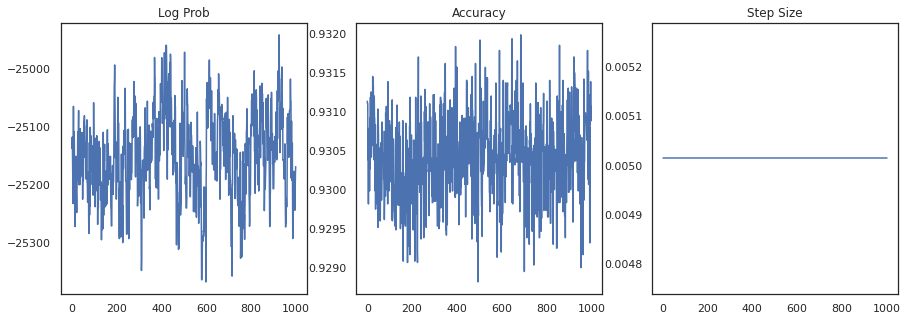
إذا قمنا بتجميع العينات ، فيمكننا حساب متوسط ​​نموذج بايزي لتحسين أدائنا.

@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
  images, labels = data
  logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
  probs = jax.nn.softmax(logits, axis=-1)
  bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
  avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
  return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')

sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')

Average Accuracy: 0.9188529253005981
BMA Accuracy: 0.9264000058174133
Accuracy Improvement: 0.0075470805168151855

يزيد متوسط ​​نموذج بايزي من دقتنا بنسبة 1٪ تقريبًا!

مثال: نظام توصية MovieLens

دعنا الآن نحاول الاستدلال باستخدام مجموعة بيانات توصيات MovieLens ، وهي مجموعة من المستخدمين وتقييماتهم للأفلام المختلفة. على وجه التحديد، ونحن يمكن أن تمثل MovieLens باعتبارها \(N \times M\) ساعة مصفوفة \(W\) حيث \(N\) هو عدد المستخدمين و \(M\) هو عدد من الأفلام. نتوقع \(N > M\). مداخل \(W_{ij}\) هي منطقية تشير أم لا المستعمل \(i\) شاهدت فيلم \(j\). لاحظ أن برنامج MovieLens يوفر تقييمات للمستخدمين ، لكننا نتجاهلها لتبسيط المشكلة.

أولاً ، سنقوم بتحميل مجموعة البيانات. سنستخدم الإصدار بمليون تقييم.

movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
          'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
          'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
          'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']

Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0...
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl…

HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value='')))
Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord
HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value='')))
Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.

سنفعل بعض تجهيزها من مجموعة البيانات للحصول على ساعة مصفوفة \(W\).

raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']

movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])

num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1

movie_titles = dict(zip(movielens['train']['movie_id'],
                        movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
                        genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
                     for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]

watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)

(6040, 3706)

يمكننا تحديد نموذج توليدي ل \(W\)، وذلك باستخدام مصفوفة الاحتمالية نموذج توكيل تجاري بسيط. ونحن نفترض كامنة \(N \times D\) مصفوفة المستخدم \(U\) وكامنة \(M \times D\) الفيلم مصفوفة \(V\)، والتي عندما تضاعف إنتاج logits من برنولي للساعة مصفوفة \(W\). ونحن سوف تشمل أيضا ناقلات التحيز للمستخدمين والأفلام، \(u\) و \(v\).

\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]

هذه مصفوفة كبيرة جدًا ؛ 6040 مستخدم و 3706 فيلم يؤدي إلى مصفوفة بها أكثر من 22 مليون مدخل. كيف نقترب من تجزئة هذا النموذج؟ حسنا، إذا افترضنا أن \(N > M\) (أي هناك المزيد من المستخدمين من الأفلام)، فإنه سيكون من المنطقي أن شارد مصفوفة ساعة عبر محور المستخدم، بحيث كل جهاز سيكون له قطعة من الساعات المصفوفة المقابلة لمجموعة فرعية من المستخدمين . على عكس المثال السابق، ومع ذلك، سيكون لدينا أيضا إلى شارد حتى \(U\) المصفوفة، نظرا لما له من التضمين لكل مستخدم، بحيث كل جهاز ستكون مسؤولة عن كسرة فخارية من \(U\) وكسرة فخارية من \(W\). من ناحية أخرى، \(V\) سيكون unsharded وتكون متزامنة عبر الأجهزة.

sharded_watch_matrix = shard(watch_matrix)

قبل نكتب لدينا run ، دعونا بسرعة مناقشة تحديات إضافية مع عملية التجزئة المحلي متغير عشوائي \(U\). عند تشغيل مؤسسة حمد الطبية، والفانيليا tfp.mcmc.HamiltonianMonteCarlo نواة سوف تذوق العزم لكل عنصر من عناصر الدولة في السلسلة. في السابق ، كانت المتغيرات العشوائية غير المقيدة فقط جزءًا من تلك الحالة ، وكانت العزم هي نفسها على كل جهاز. عندما يكون لدينا الآن sharded \(U\)، نحن بحاجة إلى أخذ عينات العزم مختلفة على كل جهاز ل \(U\)، في حين أخذ عينات من نفس العزم ل \(V\). ولتحقيق ذلك، يمكننا استخدام tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo مع Sharded توزيع العزم. بينما نستمر في إجراء الحساب المتوازي من الدرجة الأولى ، يمكننا تبسيط ذلك ، على سبيل المثال عن طريق أخذ مؤشر الحدة إلى نواة HMC.

def make_run(*,
             axis_name,
             dim=20,
             num_chains=2,
             prior_variance=1.,
             step_size=1e-2,
             num_leapfrog_steps=100,
             num_burnin_steps=1000,
             num_results=500,
             ):
  @functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
  @jax.default_matmul_precision('tensorfloat32')
  def run(key, watch_matrix):
    num_users, num_movies = watch_matrix.shape

    Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)

    def prior_fn():
      user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
      user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
      movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
      movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
      return (user_embeddings, user_bias, movie_embeddings, movie_bias)
    prior = tfed.JointDistributionCoroutine(prior_fn)

    def model_fn():
      user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
      logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
                + user_bias[..., :, None] + movie_bias[..., None, :])
      yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
    model = tfed.JointDistributionCoroutine(model_fn)

    init_key, sample_key = random.split(key)
    initial_state = prior.sample(seed=init_key, sample_shape=num_chains)

    def target_log_prob(*state):
      return model.log_prob((*state, watch_matrix))

    momentum_distribution = tfed.JointDistributionSequential([
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
    ])

    # We pass in momentum_distribution here to ensure that the momenta for 
    # user_embeddings and user_bias are also sharded
    kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
                                                      num_leapfrog_steps,
                                                      momentum_distribution=momentum_distribution)

    num_adaptation_steps = int(0.8 * num_burnin_steps)
    kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)

    def trace_fn(state, pkr):
      return {
        'log_prob': target_log_prob(*state),
        'log_accept_ratio': pkr.inner_results.log_accept_ratio,
      }
    return tfm.sample_chain(
        num_results, initial_state,
        kernel=kernel,
        num_burnin_steps=num_burnin_steps,
        trace_fn=trace_fn,
        seed=sample_key)
  return run

ونحن مرة أخرى سوف تشغيله مرة واحدة إلى ذاكرة التخزين المؤقت المترجمة run .

%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 56 s, sys: 1min 24s, total: 2min 20s
Wall time: 3min 35s

الآن سنقوم بتشغيله مرة أخرى دون تحميل النفقات العامة.

%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s
Wall time: 3min 1s

يبدو أننا أكملنا حوالي 150000 خطوة قفزة في حوالي 3 دقائق ، أي حوالي 83 خطوة قفزة في الثانية! دعنا نرسم نسبة القبول وكثافة اللوغاريتمات لعيناتنا.

fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
  ax.plot(val[0]) # Indexing into a sharded array, each element is the same
  ax.set_title(key);

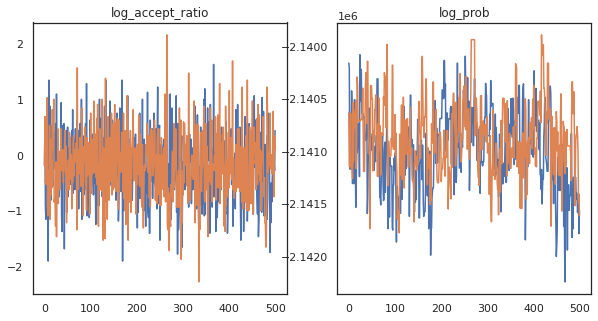
الآن بعد أن أصبح لدينا بعض العينات من سلسلة ماركوف ، فلنستخدمها لعمل بعض التنبؤات. أولاً ، دعنا نستخرج كل مكون. تذكر أن user_embeddings و user_bias هي الانقسام عبر الجهاز، لذلك نحن بحاجة إلى سلسلة لدينا ShardedArray للحصول على كل منهم. من ناحية أخرى، movie_embeddings و movie_bias هي نفسها على كل جهاز، حتى نتمكن من مجرد اختيار القيمة من قشرة الأولى. سنستخدم العادية numpy لنسخ القيم من الخلف TPUs إلى وحدة المعالجة المركزية.

user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')

User embeddings: (500, 2, 6040, 20)
User bias: (500, 2, 6040)
Movie embeddings: (500, 2, 3706, 20)
Movie bias: (500, 2, 3706)

دعنا نحاول بناء نظام توصية بسيط يستخدم عدم اليقين الذي تم تسجيله في هذه العينات. لنكتب أولاً دالة تصنف الأفلام وفقًا لاحتمال المشاهدة.

@jax.jit
def recommend(sample, user_id):
  user_embeddings, user_bias, movie_embeddings, movie_bias = sample
  movie_logits = (
      jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
      + user_bias[user_id] + movie_bias)
  return movie_logits.argsort()[::-1]

يمكننا الآن كتابة وظيفة تتكرر في جميع العينات ولكل منها ، تختار الفيلم الأعلى تصنيفًا الذي لم يشاهده المستخدم بالفعل. يمكننا بعد ذلك رؤية أعداد جميع الأفلام الموصى بها عبر العينات.

def get_recommendations(user_id): 
  movie_ids = []
  already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
  for i in range(500):
    for j in range(2):
      sample = jax.tree_map(lambda x: x[i, j], samples)
      ranking = recommend(sample, user_id)
      for movie_id in ranking:
        if int(movie_id) not in already_watched:
          movie_ids.append(movie_id)
          break
  return movie_ids

def plot_recommendations(movie_ids, ax=None):
  titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
  ax = ax or plt.gca()
  names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
  ax.bar(names, counts)
  ax.set_xticklabels(names, rotation=90)

لنأخذ المستخدم الذي شاهد معظم الأفلام مقابل المستخدم الذي شاهد أقل عدد من الأفلام.

user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])

2314 20

نأمل نظامنا أكبر من اليقين حول user_most من user_least ، بالنظر إلى أن لدينا المزيد من المعلومات حول ما يفرز من الأفلام user_most هو أكثر عرضة للمشاهدة.

fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');

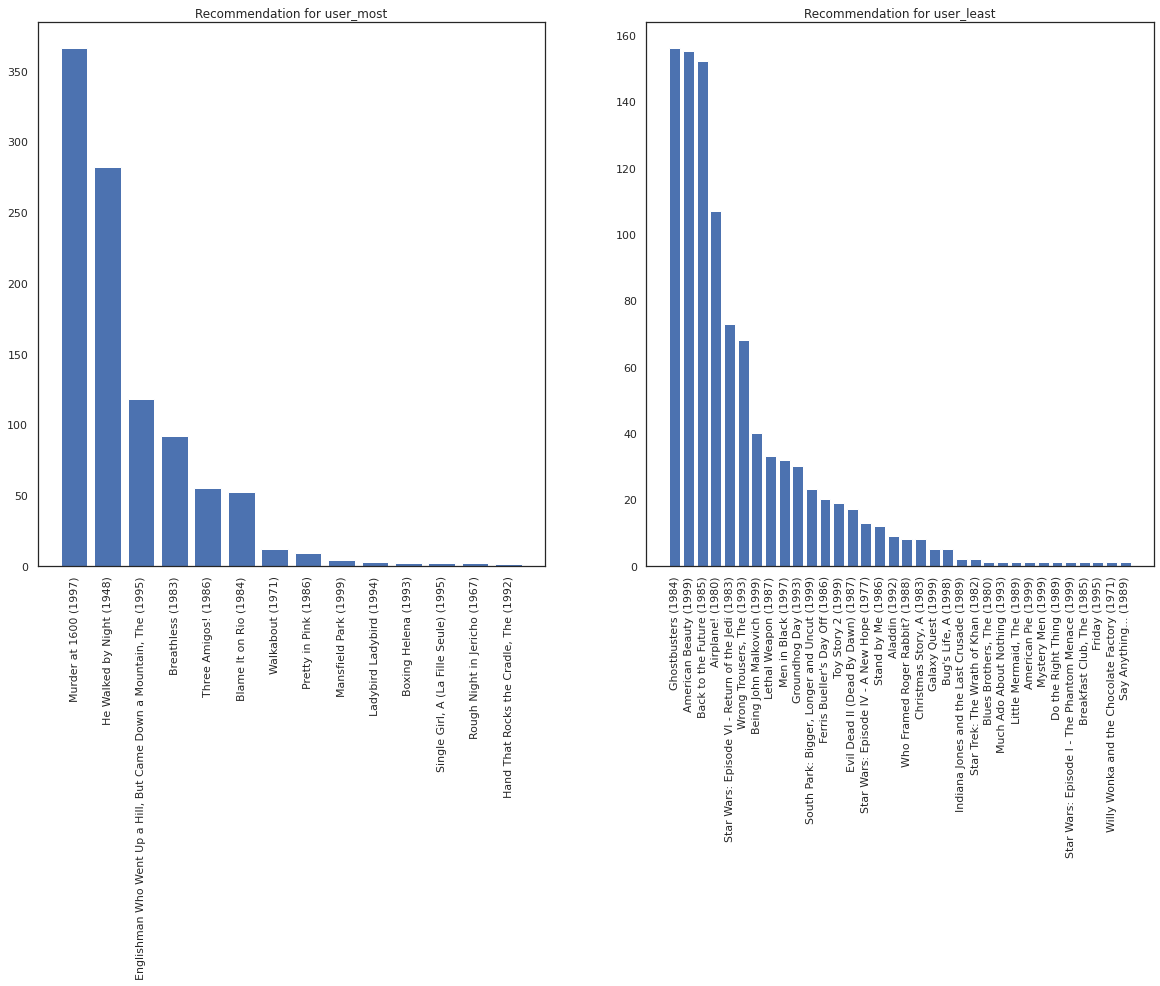
ونحن نرى أن هناك المزيد من التباين في توصياتنا لل user_least يعكس لدينا المزيد من عدم اليقين في تفضيلات مراقبتهم.

يمكننا أيضًا الاطلاع على أنواع الأفلام الموصى بها.

most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');

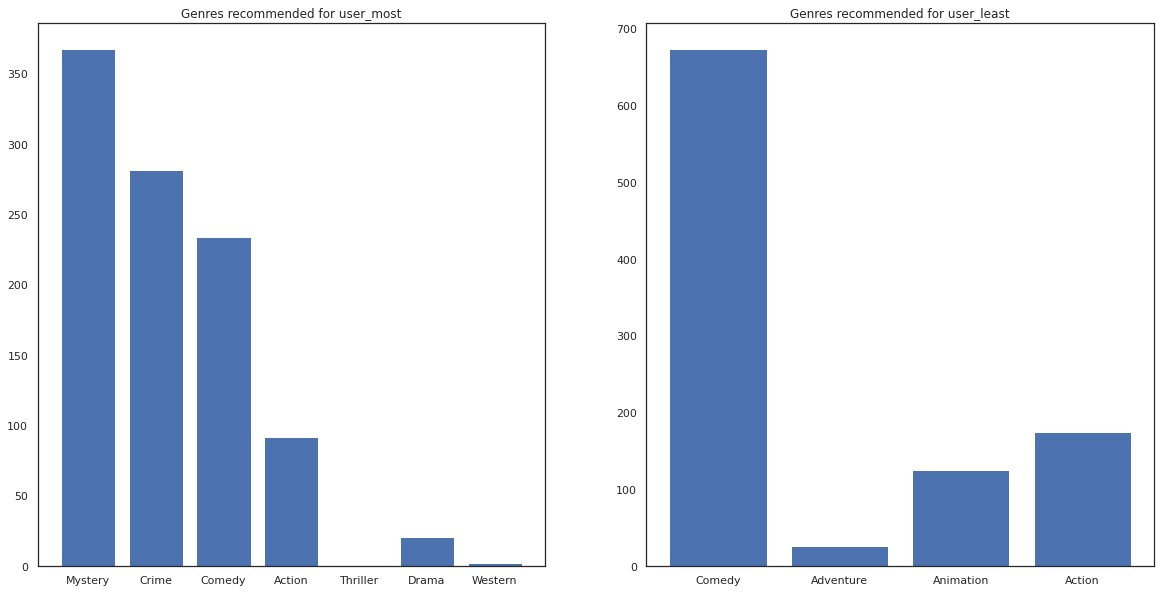
user_most شهدت الكثير من الأفلام والموصى بها أكثر الأنواع المتخصصة مثل الغموض والجريمة في حين user_least لم يشاهد العديد من الأفلام، وأوصى المزيد من الأفلام السائدة، التي الكوميديا الانحراف والعمل.