Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Máy tính xách tay này reimplements và mở rộng “phân tích điểm đổi” Bayesian ví dụ từ các tài liệu pymc3 .
Điều kiện tiên quyết
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (15,8)
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
Dataset
Bộ dữ liệu là từ đây . Lưu ý, có một phiên bản của ví dụ này nổi xung quanh , nhưng nó đã “mất tích” dữ liệu - trong trường hợp này bạn cần phải quy cho các giá trị bị mất tích. (Nếu không, mô hình của bạn sẽ không bao giờ để lại các tham số ban đầu vì hàm khả năng sẽ không được xác định.)
disaster_data = np.array([ 4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
2, 2, 3, 4, 2, 1, 3, 2, 2, 1, 1, 1, 1, 3, 0, 0,
1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
3, 3, 1, 1, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1])
years = np.arange(1851, 1962)
plt.plot(years, disaster_data, 'o', markersize=8);
plt.ylabel('Disaster count')
plt.xlabel('Year')
plt.title('Mining disaster data set')
plt.show()
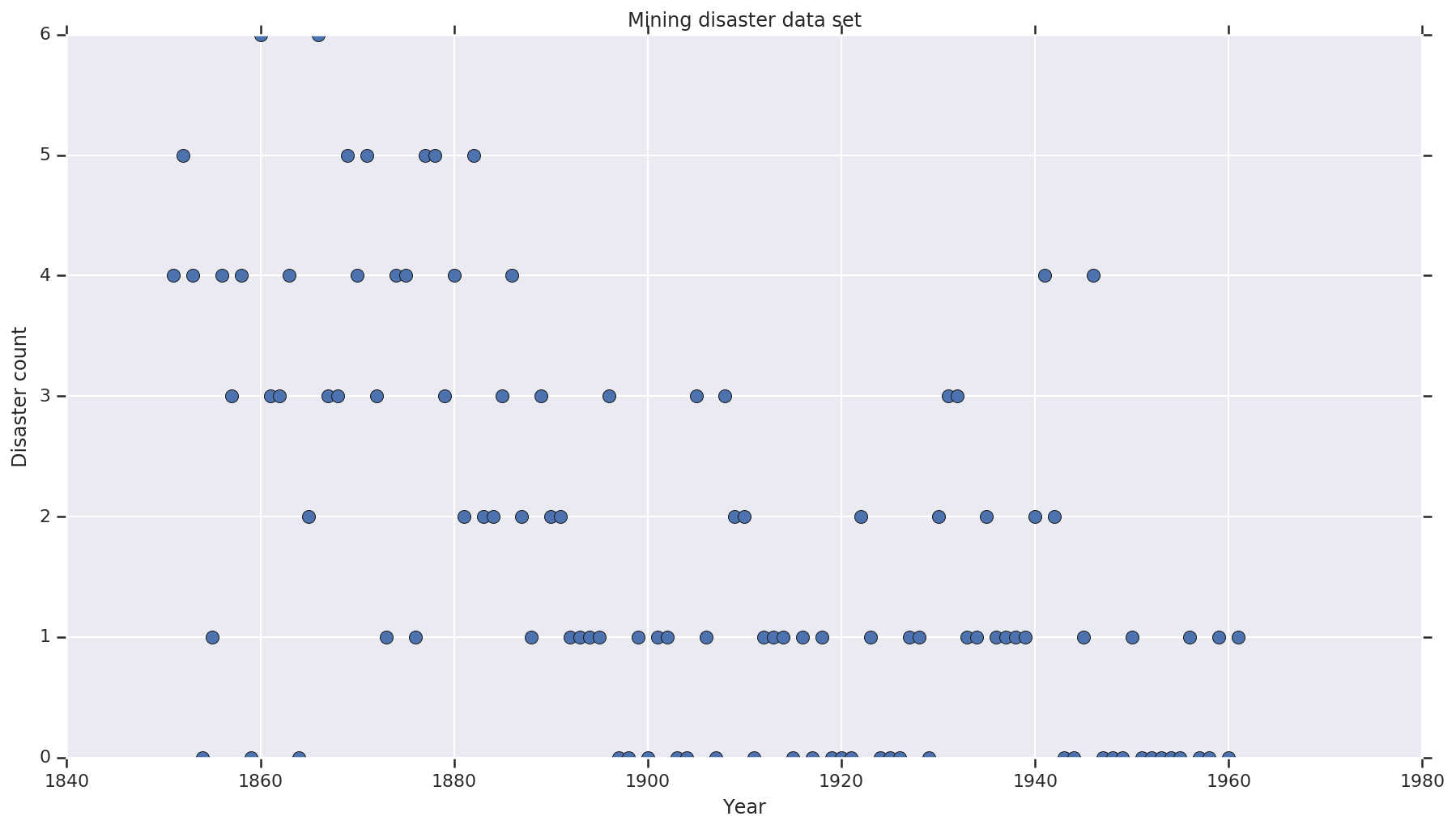
Mô hình xác suất
Mô hình giả định một “điểm chuyển đổi” (ví dụ: một năm mà các quy định về an toàn đã thay đổi) và tỷ lệ thiên tai được phân phối theo Poisson với tỷ lệ không đổi (nhưng có thể khác nhau) trước và sau điểm chuyển đổi đó.
Số lượng thảm họa thực tế được cố định (quan sát); bất kỳ mẫu nào của mô hình này sẽ cần xác định cả điểm chuyển mạch và tỷ lệ "sớm" và "muộn" của thảm họa.
Mô hình ban đầu từ ví dụ tài liệu pymc3 :
\[ \begin{align*} (D_t|s,e,l)&\sim \text{Poisson}(r_t), \\ & \,\quad\text{with}\; r_t = \begin{cases}e & \text{if}\; t < s\\l &\text{if}\; t \ge s\end{cases} \\ s&\sim\text{Discrete Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
Tuy nhiên, giá trị trung bình tỷ lệ thảm họa \(r_t\) có một gián đoạn tại switchpoint \(s\), mà làm cho nó không khả vi. Vì vậy nó không cung cấp tín hiệu gradient cho (HMC) thuật toán Hamiltonian Monte Carlo - nhưng vì \(s\) trước là liên tục, dự phòng HMC để bước ngẫu nhiên là tốt, đủ để thấy các lĩnh vực khối lượng xác suất cao trong ví dụ này.
Là một mô hình thứ hai, chúng tôi thay đổi mô hình ban đầu sử dụng một sigmoid “chuyển đổi” giữa e và l để làm cho quá trình chuyển đổi khả vi, và sử dụng một phân bố đều liên tục cho switchpoint \(s\). (Người ta có thể tranh luận rằng mô hình này đúng hơn với thực tế, vì một "chuyển đổi" về tỷ lệ trung bình có thể sẽ được kéo dài trong nhiều năm.) Do đó, mô hình mới là:
\[ \begin{align*} (D_t|s,e,l)&\sim\text{Poisson}(r_t), \\ & \,\quad \text{with}\; r_t = e + \frac{1}{1+\exp(s-t)}(l-e) \\ s&\sim\text{Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
Trong trường hợp không có thêm thông tin chúng tôi giả định \(r_e = r_l = 1\) như tham số cho priors. Chúng tôi sẽ chạy cả hai mô hình và so sánh kết quả suy luận của chúng.
def disaster_count_model(disaster_rate_fn):
disaster_count = tfd.JointDistributionNamed(dict(
e=tfd.Exponential(rate=1.),
l=tfd.Exponential(rate=1.),
s=tfd.Uniform(0., high=len(years)),
d_t=lambda s, l, e: tfd.Independent(
tfd.Poisson(rate=disaster_rate_fn(np.arange(len(years)), s, l, e)),
reinterpreted_batch_ndims=1)
))
return disaster_count
def disaster_rate_switch(ys, s, l, e):
return tf.where(ys < s, e, l)
def disaster_rate_sigmoid(ys, s, l, e):
return e + tf.sigmoid(ys - s) * (l - e)
model_switch = disaster_count_model(disaster_rate_switch)
model_sigmoid = disaster_count_model(disaster_rate_sigmoid)
Đoạn mã trên xác định mô hình thông qua các bản phân phối JointDistributionSequential. Các disaster_rate chức năng được gọi với một mảng của [0, ..., len(years)-1] để tạo ra một vector của len(years) các biến ngẫu nhiên - những năm trước switchpoint là early_disaster_rate , những người sau late_disaster_rate (modulo sự chuyển tiếp sigmoid).
Dưới đây là kiểm tra sự tỉnh táo để đảm bảo rằng chức năng kiểm tra nhật ký mục tiêu hoạt động tốt:
def target_log_prob_fn(model, s, e, l):
return model.log_prob(s=s, e=e, l=l, d_t=disaster_data)
models = [model_switch, model_sigmoid]
print([target_log_prob_fn(m, 40., 3., .9).numpy() for m in models]) # Somewhat likely result
print([target_log_prob_fn(m, 60., 1., 5.).numpy() for m in models]) # Rather unlikely result
print([target_log_prob_fn(m, -10., 1., 1.).numpy() for m in models]) # Impossible result
[-176.94559, -176.28717] [-371.3125, -366.8816] [-inf, -inf]
HMC để thực hiện suy luận Bayes
Chúng tôi xác định số lượng kết quả và các bước ghi cần thiết; mã chủ yếu theo mô hình sau khi các tài liệu của tfp.mcmc.HamiltonianMonteCarlo . Nó sử dụng kích thước bước thích ứng (nếu không thì kết quả rất nhạy cảm với giá trị kích thước bước đã chọn). Chúng tôi sử dụng các giá trị của một làm trạng thái ban đầu của chuỗi.
Đây không phải là câu chuyện đầy đủ mặc dù. Nếu bạn quay lại định nghĩa mô hình ở trên, bạn sẽ lưu ý rằng một số phân phối xác suất không được xác định rõ ràng trên toàn bộ dòng số thực. Vì vậy chúng tôi hạn chế không gian mà HMC phải kiểm tra bằng cách gói kernel HMC với một TransformedTransitionKernel chỉ định bijectors mong muốn chuyển đổi số thực vào miền mà phân bố xác suất được xác định trên (xem chú thích trong mã dưới đây).
num_results = 10000
num_burnin_steps = 3000
@tf.function(autograph=False, jit_compile=True)
def make_chain(target_log_prob_fn):
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.05,
num_leapfrog_steps=3),
bijector=[
# The switchpoint is constrained between zero and len(years).
# Hence we supply a bijector that maps the real numbers (in a
# differentiable way) to the interval (0;len(yers))
tfb.Sigmoid(low=0., high=tf.cast(len(years), dtype=tf.float32)),
# Early and late disaster rate: The exponential distribution is
# defined on the positive real numbers
tfb.Softplus(),
tfb.Softplus(),
])
kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=int(0.8*num_burnin_steps))
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
# The three latent variables
tf.ones([], name='init_switchpoint'),
tf.ones([], name='init_early_disaster_rate'),
tf.ones([], name='init_late_disaster_rate'),
],
trace_fn=None,
kernel=kernel)
return states
switch_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_switch, *args))]
sigmoid_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_sigmoid, *args))]
switchpoint, early_disaster_rate, late_disaster_rate = zip(
switch_samples, sigmoid_samples)
Chạy song song cả hai mô hình:
Hình dung kết quả
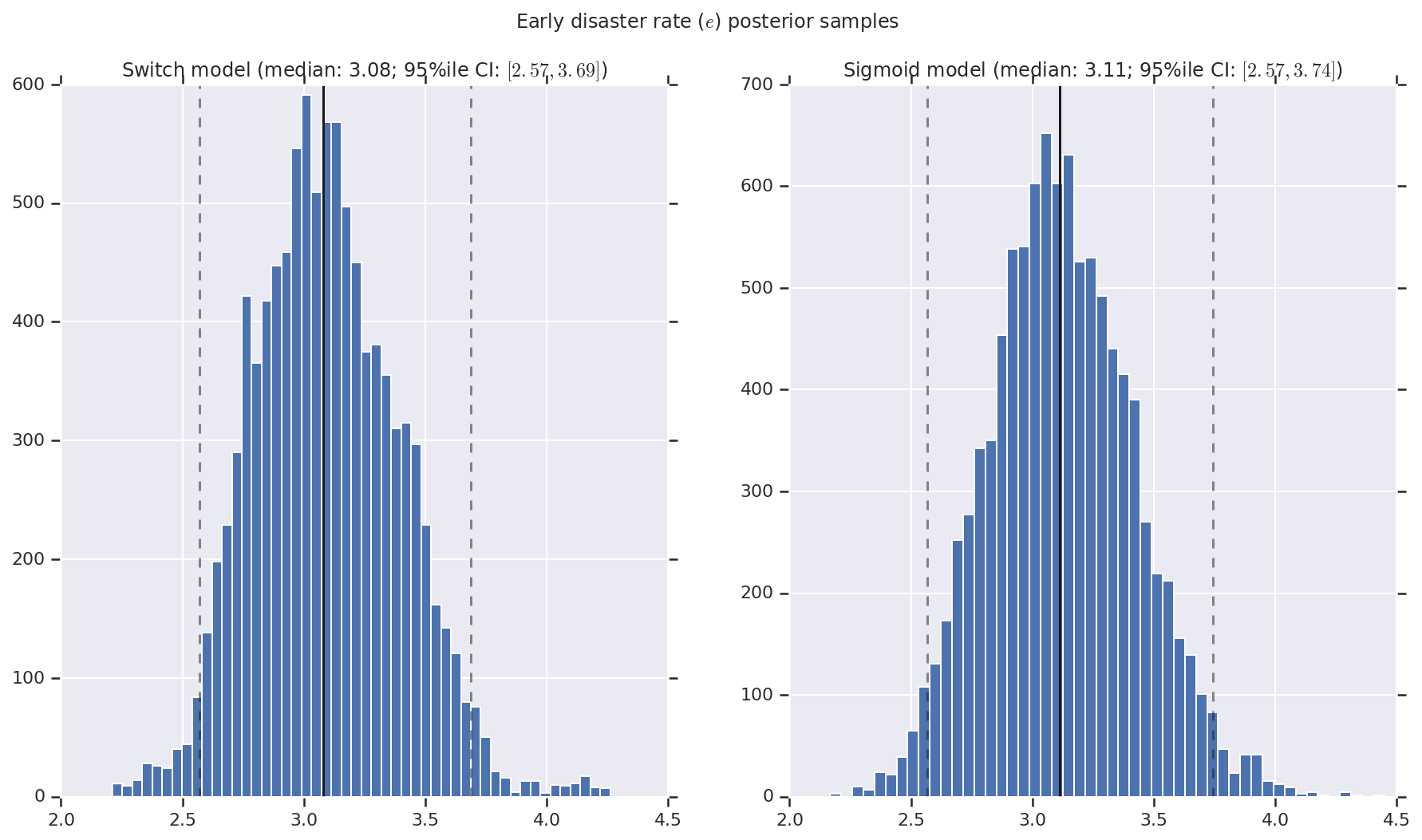
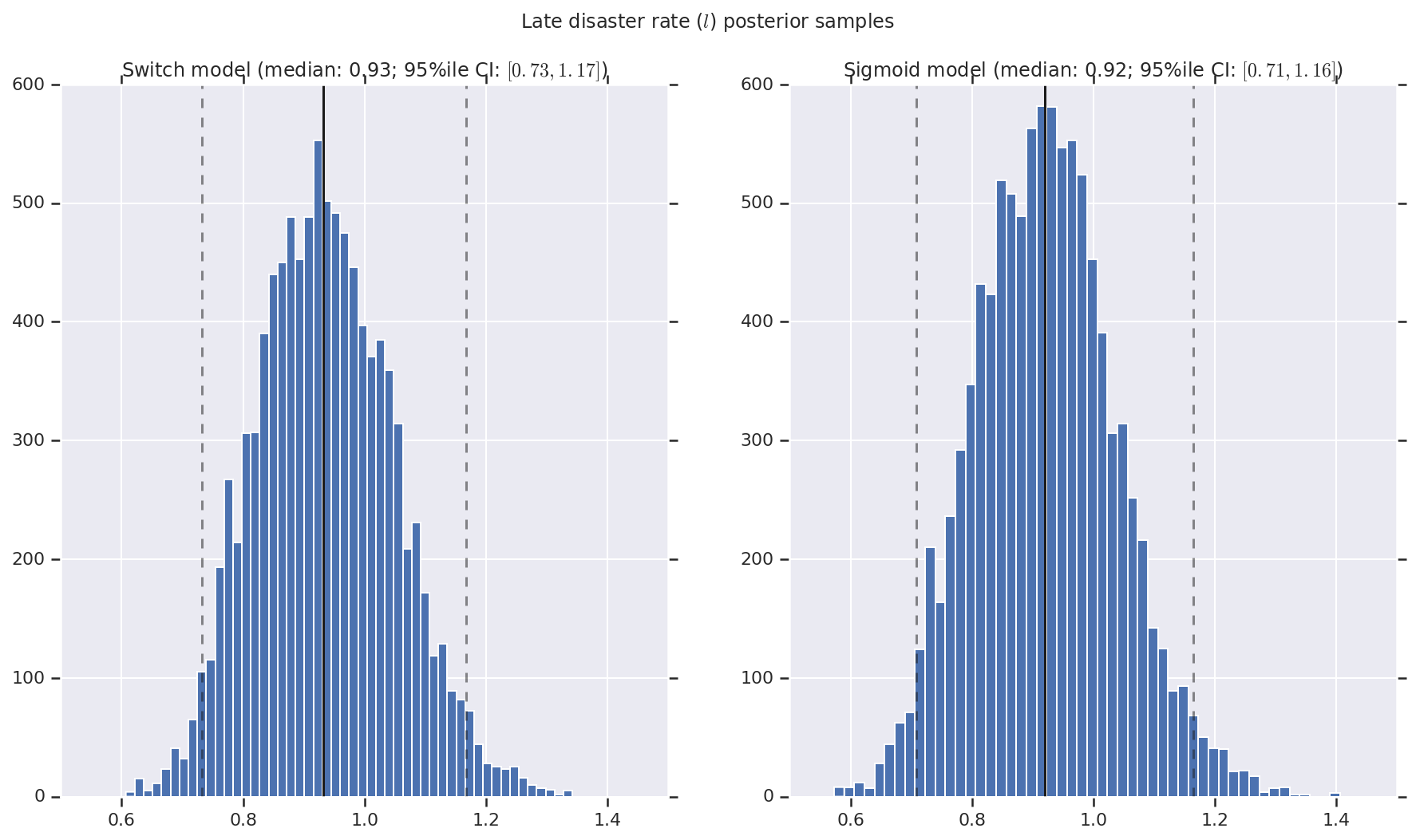
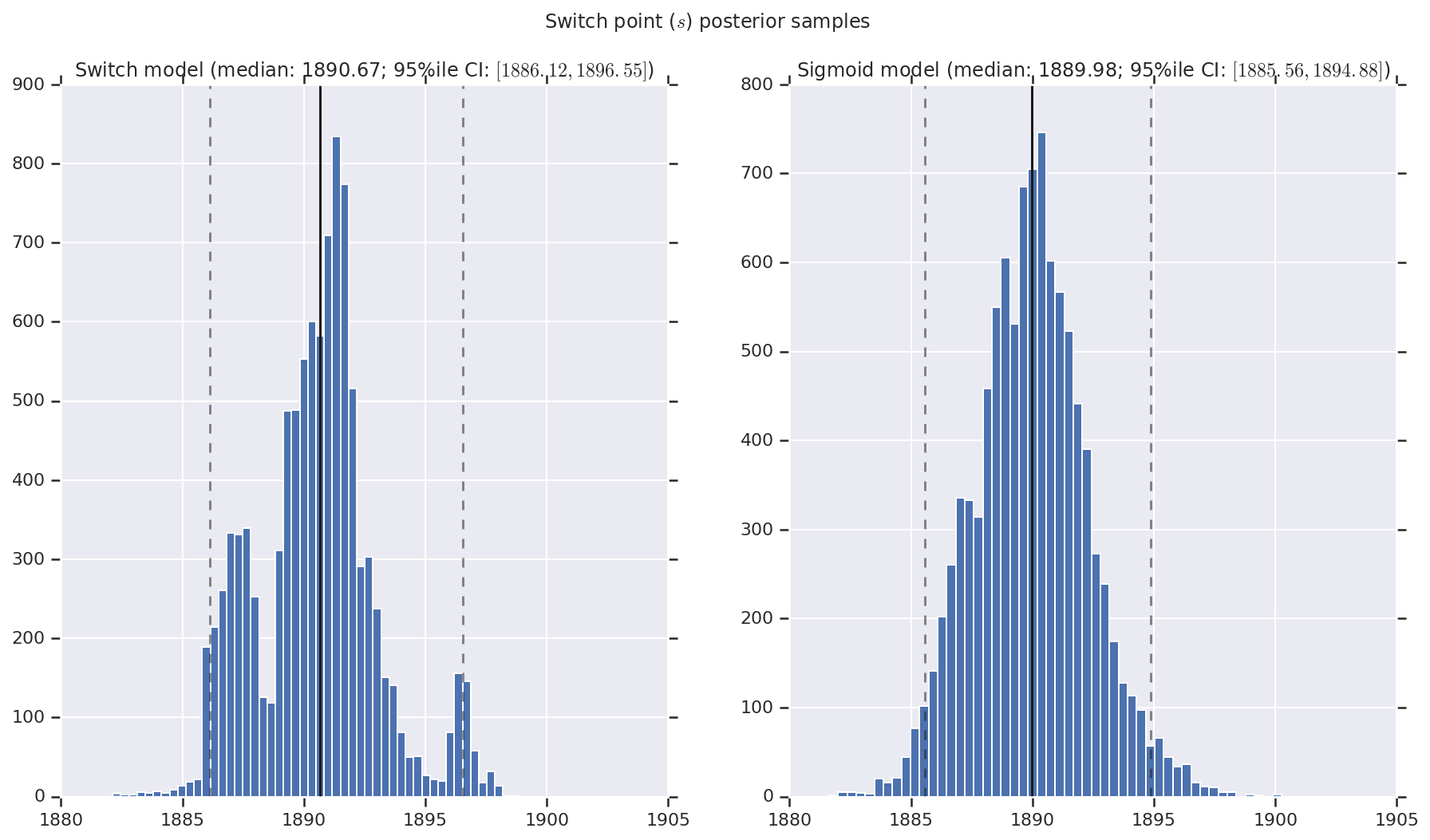
Chúng tôi hình dung kết quả dưới dạng biểu đồ của các mẫu phân bố sau cho tỷ lệ thiên tai sớm và muộn, cũng như điểm chuyển mạch. Biểu đồ được phủ bởi một đường liền nét thể hiện trung vị mẫu, cũng như giới hạn khoảng tin cậy 95% ile dưới dạng đường đứt nét.
def _desc(v):
return '(median: {}; 95%ile CI: $[{}, {}]$)'.format(
*np.round(np.percentile(v, [50, 2.5, 97.5]), 2))
for t, v in [
('Early disaster rate ($e$) posterior samples', early_disaster_rate),
('Late disaster rate ($l$) posterior samples', late_disaster_rate),
('Switch point ($s$) posterior samples', years[0] + switchpoint),
]:
fig, ax = plt.subplots(nrows=1, ncols=2, sharex=True)
for (m, i) in (('Switch', 0), ('Sigmoid', 1)):
a = ax[i]
a.hist(v[i], bins=50)
a.axvline(x=np.percentile(v[i], 50), color='k')
a.axvline(x=np.percentile(v[i], 2.5), color='k', ls='dashed', alpha=.5)
a.axvline(x=np.percentile(v[i], 97.5), color='k', ls='dashed', alpha=.5)
a.set_title(m + ' model ' + _desc(v[i]))
fig.suptitle(t)
plt.show()