Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Este notebook reimplementa e estende a “análise de ponto de Change” Bayesian exemplo da documentação pymc3 .
Pré-requisitos
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (15,8)
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
Conjunto de dados
O conjunto de dados é a partir daqui . Note, há uma outra versão deste exemplo flutuando ao redor , mas tem “falta” de dados - caso em que você precisa para imputar valores ausentes. (Caso contrário, seu modelo nunca deixará seus parâmetros iniciais porque a função de verossimilhança ficará indefinida.)
disaster_data = np.array([ 4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
2, 2, 3, 4, 2, 1, 3, 2, 2, 1, 1, 1, 1, 3, 0, 0,
1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
3, 3, 1, 1, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1])
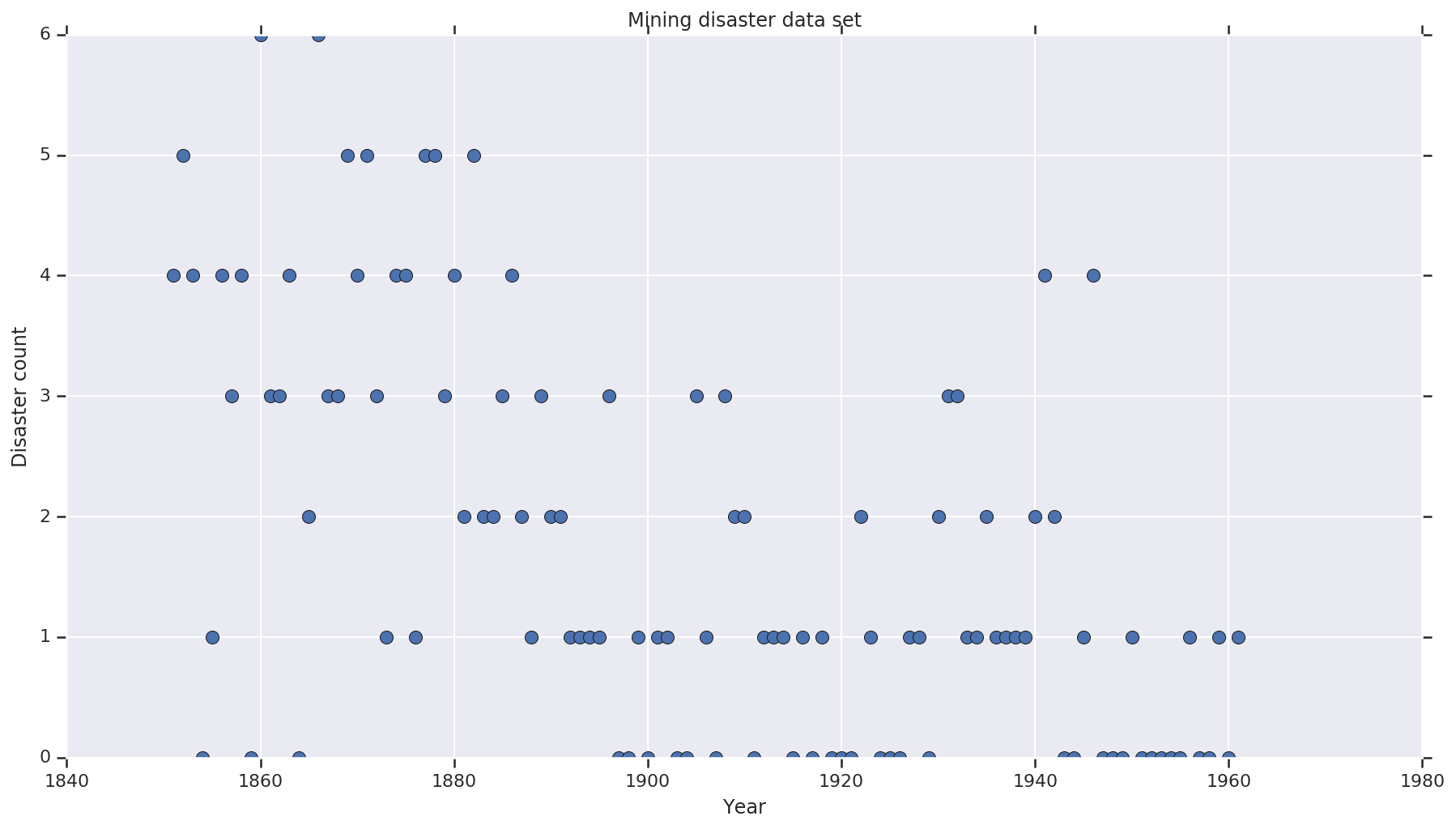
years = np.arange(1851, 1962)
plt.plot(years, disaster_data, 'o', markersize=8);
plt.ylabel('Disaster count')
plt.xlabel('Year')
plt.title('Mining disaster data set')
plt.show()
Modelo Probabilístico
O modelo assume um “ponto de troca” (por exemplo, um ano durante o qual os regulamentos de segurança mudaram) e a taxa de desastres distribuída por Poisson com taxas constantes (mas potencialmente diferentes) antes e depois desse ponto de troca.
A contagem real de desastres é fixa (observada); qualquer amostra desse modelo precisará especificar tanto o ponto de mudança quanto a taxa de desastres “inicial” e “tardia”.
Modelo original de exemplo documentação pymc3 :
\[ \begin{align*} (D_t|s,e,l)&\sim \text{Poisson}(r_t), \\ & \,\quad\text{with}\; r_t = \begin{cases}e & \text{if}\; t < s\\l &\text{if}\; t \ge s\end{cases} \\ s&\sim\text{Discrete Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
No entanto, a média taxa de desastre \(r_t\) tem uma descontinuidade na switchpoint \(s\), o que faz com que não diferenciável. Assim, não fornece nenhum sinal de gradiente para o algoritmo Hamiltonian Monte Carlo (HMC) - mas porque o \(s\) antes é contínua, fallback do HMC para um passeio aleatório é bom o suficiente para encontrar as áreas de massa de alta probabilidade neste exemplo.
Como um segundo modelo, modificar o modelo original usando um sigmóide “switch” entre E e L para fazer a transição diferenciável, e usar uma distribuição uniforme contínua para o switchpoint \(s\). (Pode-se argumentar que este modelo é mais fiel à realidade, já que uma "mudança" na taxa média provavelmente seria estendida ao longo de vários anos.) O novo modelo é assim:
\[ \begin{align*} (D_t|s,e,l)&\sim\text{Poisson}(r_t), \\ & \,\quad \text{with}\; r_t = e + \frac{1}{1+\exp(s-t)}(l-e) \\ s&\sim\text{Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
Na ausência de mais informações assumimos \(r_e = r_l = 1\) como parâmetros para os priores. Executaremos os dois modelos e compararemos seus resultados de inferência.
def disaster_count_model(disaster_rate_fn):
disaster_count = tfd.JointDistributionNamed(dict(
e=tfd.Exponential(rate=1.),
l=tfd.Exponential(rate=1.),
s=tfd.Uniform(0., high=len(years)),
d_t=lambda s, l, e: tfd.Independent(
tfd.Poisson(rate=disaster_rate_fn(np.arange(len(years)), s, l, e)),
reinterpreted_batch_ndims=1)
))
return disaster_count
def disaster_rate_switch(ys, s, l, e):
return tf.where(ys < s, e, l)
def disaster_rate_sigmoid(ys, s, l, e):
return e + tf.sigmoid(ys - s) * (l - e)
model_switch = disaster_count_model(disaster_rate_switch)
model_sigmoid = disaster_count_model(disaster_rate_sigmoid)
O código acima define o modelo por meio de distribuições JointDistributionSequential. Os disaster_rate funções são chamadas com uma matriz de [0, ..., len(years)-1] para produzir um vector de len(years) variáveis aleatórias - os anos antes da switchpoint são early_disaster_rate , aqueles depois late_disaster_rate (modulo do transição sigmóide).
Aqui está uma verificação de sanidade se a função de prob log de destino é sã:
def target_log_prob_fn(model, s, e, l):
return model.log_prob(s=s, e=e, l=l, d_t=disaster_data)
models = [model_switch, model_sigmoid]
print([target_log_prob_fn(m, 40., 3., .9).numpy() for m in models]) # Somewhat likely result
print([target_log_prob_fn(m, 60., 1., 5.).numpy() for m in models]) # Rather unlikely result
print([target_log_prob_fn(m, -10., 1., 1.).numpy() for m in models]) # Impossible result
[-176.94559, -176.28717] [-371.3125, -366.8816] [-inf, -inf]
HMC para fazer inferência bayesiana
Nós definimos o número de resultados e etapas de burn-in necessárias; o código é mais modelado após a documentação de tfp.mcmc.HamiltonianMonteCarlo . Ele usa um tamanho de passo adaptável (caso contrário, o resultado é muito sensível ao valor do tamanho do passo escolhido). Usamos valores de um como o estado inicial da cadeia.
Esta não é a história completa. Se você voltar à definição do modelo acima, notará que algumas das distribuições de probabilidade não estão bem definidas em toda a linha de número real. Portanto, restringir o espaço que HMC examinará envolvendo o kernel HMC com um TransformedTransitionKernel que especifica o bijectors frente para transformar os números reais sobre o domínio que a distribuição de probabilidade é definido em (ver comentários no código abaixo).
num_results = 10000
num_burnin_steps = 3000
@tf.function(autograph=False, jit_compile=True)
def make_chain(target_log_prob_fn):
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.05,
num_leapfrog_steps=3),
bijector=[
# The switchpoint is constrained between zero and len(years).
# Hence we supply a bijector that maps the real numbers (in a
# differentiable way) to the interval (0;len(yers))
tfb.Sigmoid(low=0., high=tf.cast(len(years), dtype=tf.float32)),
# Early and late disaster rate: The exponential distribution is
# defined on the positive real numbers
tfb.Softplus(),
tfb.Softplus(),
])
kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=int(0.8*num_burnin_steps))
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
# The three latent variables
tf.ones([], name='init_switchpoint'),
tf.ones([], name='init_early_disaster_rate'),
tf.ones([], name='init_late_disaster_rate'),
],
trace_fn=None,
kernel=kernel)
return states
switch_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_switch, *args))]
sigmoid_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_sigmoid, *args))]
switchpoint, early_disaster_rate, late_disaster_rate = zip(
switch_samples, sigmoid_samples)
Execute os dois modelos em paralelo:
Visualize o resultado
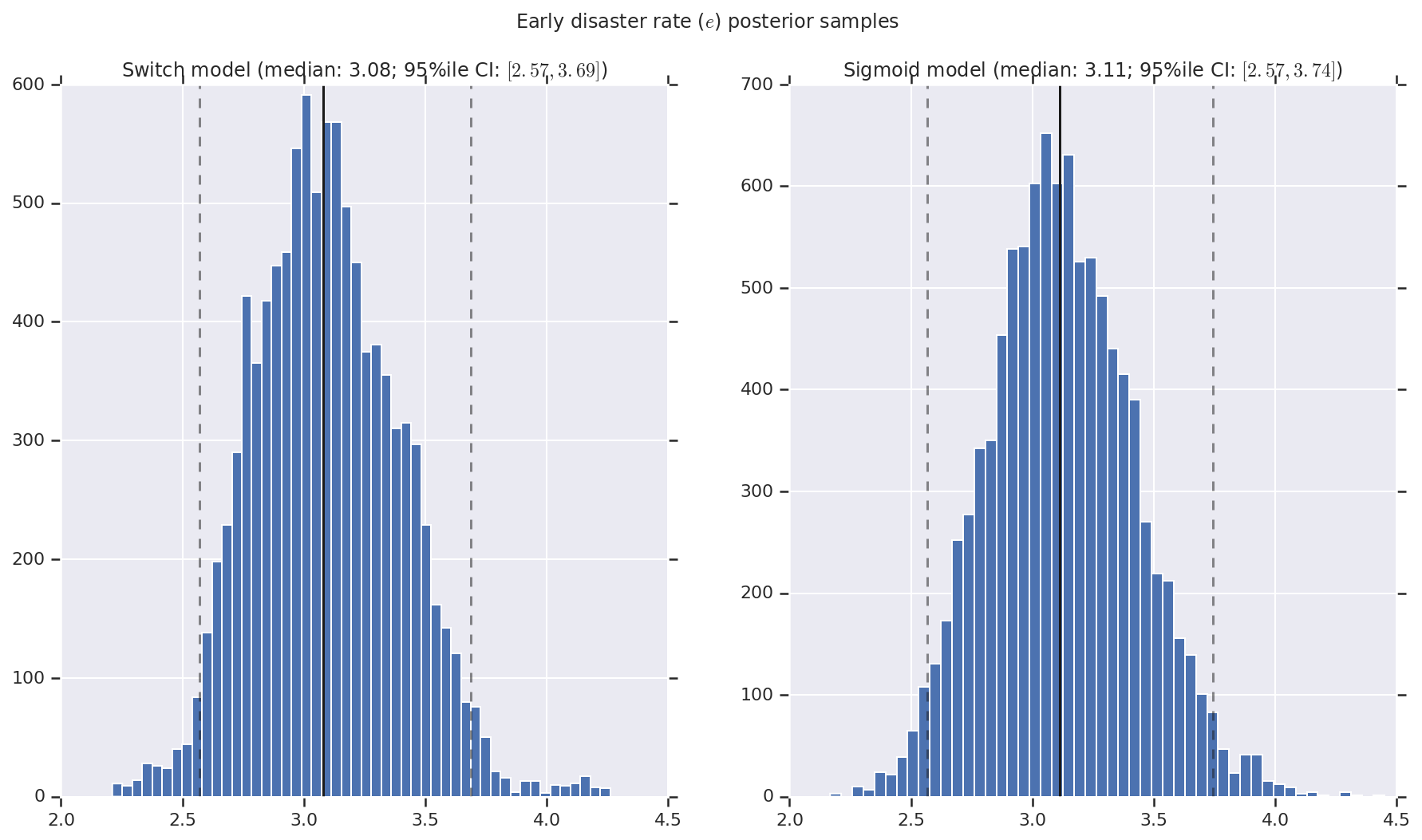
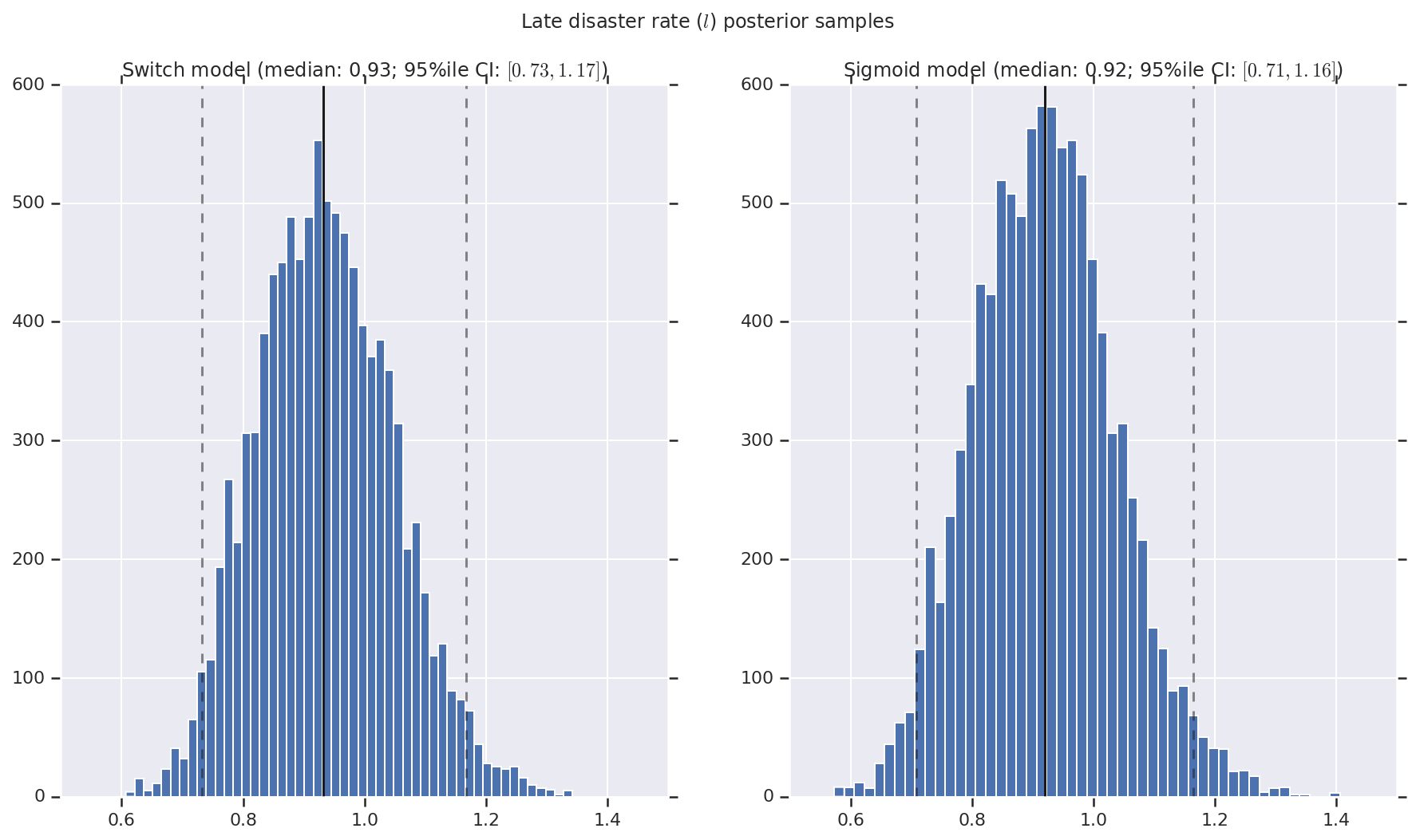
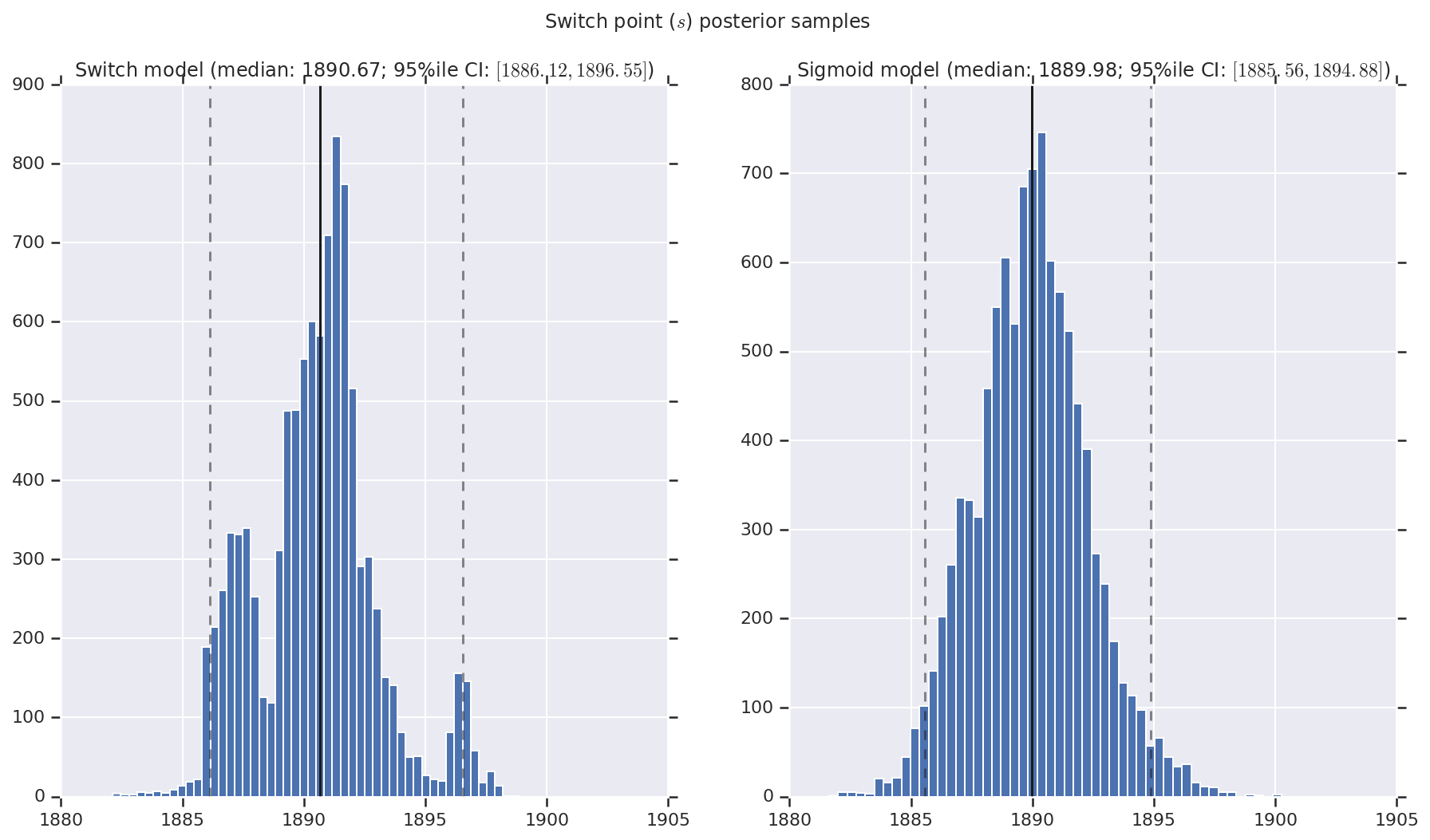
Visualizamos o resultado como histogramas de amostras da distribuição posterior para a taxa de desastre inicial e tardia, bem como o ponto de mudança. Os histogramas são sobrepostos com uma linha sólida representando a mediana da amostra, bem como os limites de intervalo confiáveis de 95% como linhas tracejadas.
def _desc(v):
return '(median: {}; 95%ile CI: $[{}, {}]$)'.format(
*np.round(np.percentile(v, [50, 2.5, 97.5]), 2))
for t, v in [
('Early disaster rate ($e$) posterior samples', early_disaster_rate),
('Late disaster rate ($l$) posterior samples', late_disaster_rate),
('Switch point ($s$) posterior samples', years[0] + switchpoint),
]:
fig, ax = plt.subplots(nrows=1, ncols=2, sharex=True)
for (m, i) in (('Switch', 0), ('Sigmoid', 1)):
a = ax[i]
a.hist(v[i], bins=50)
a.axvline(x=np.percentile(v[i], 50), color='k')
a.axvline(x=np.percentile(v[i], 2.5), color='k', ls='dashed', alpha=.5)
a.axvline(x=np.percentile(v[i], 97.5), color='k', ls='dashed', alpha=.5)
a.set_title(m + ' model ' + _desc(v[i]))
fig.suptitle(t)
plt.show()