Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Notebook ten reimplements i rozszerza Bayesa „Zmień analizę Point” przykład z dokumentacją pymc3 .
Warunki wstępne
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (15,8)
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
Zbiór danych
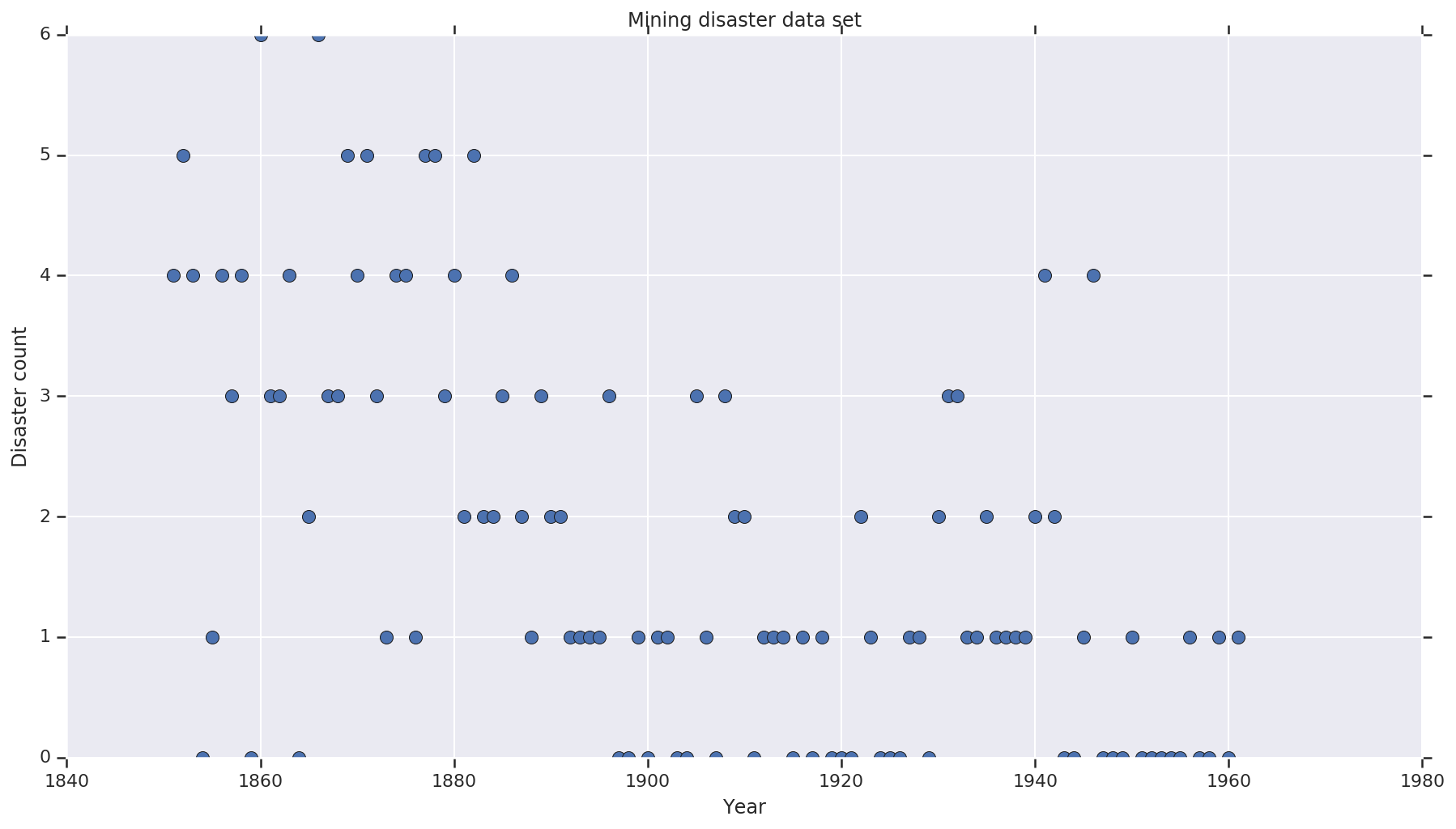
Zbiór danych jest od tutaj . Uwaga, nie ma innej wersji tego przykładu pływających wokół , ale to „brakujące” danych - w takim przypadku, że trzeba przypisać brakujące wartości. (W przeciwnym razie Twój model nigdy nie opuści swoich początkowych parametrów, ponieważ funkcja prawdopodobieństwa będzie niezdefiniowana).
disaster_data = np.array([ 4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
2, 2, 3, 4, 2, 1, 3, 2, 2, 1, 1, 1, 1, 3, 0, 0,
1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
3, 3, 1, 1, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1])
years = np.arange(1851, 1962)
plt.plot(years, disaster_data, 'o', markersize=8);
plt.ylabel('Disaster count')
plt.xlabel('Year')
plt.title('Mining disaster data set')
plt.show()
Model probabilistyczny
Model zakłada „punkt zmiany” (np. rok, w którym zmieniły się przepisy dotyczące bezpieczeństwa) oraz wskaźnik klęsk żywiołowych rozłożonych przez Poissona ze stałymi (ale potencjalnie różnymi) wskaźnikami przed i po tym punkcie zmiany.
Rzeczywista liczba katastrof jest ustalona (obserwowana); każda próbka tego modelu będzie musiała określić zarówno punkt przełączenia, jak i „wczesny” i „późny” wskaźnik katastrof.
Oryginalny model z przykładu dokumentacji pymc3 :
\[ \begin{align*} (D_t|s,e,l)&\sim \text{Poisson}(r_t), \\ & \,\quad\text{with}\; r_t = \begin{cases}e & \text{if}\; t < s\\l &\text{if}\; t \ge s\end{cases} \\ s&\sim\text{Discrete Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
Jednak średni wskaźnik katastrofa \(r_t\) ma nieciągłość w przełączeniowych \(s\), co sprawia, że nie różniczkowalna. W ten sposób zapewnia, że nie ma sygnału gradientu algorytmu Hamiltona Monte Carlo (HMC) - ale dlatego, że \(s\) przed jest ciągła, awaryjna HMC do błądzenia losowego jest wystarczająco dobry, aby znaleźć obszary o wysokiej masie prawdopodobieństwa w tym przykładzie.
W drugim modelu, że modyfikację pierwotnego modelu z wykorzystaniem esicy „switch” pomiędzy E i L dokonać przejścia różniczkowalną i użyć ciągły rozkład jednolity dla przełączeniowych \(s\). (Można argumentować, że ten model jest bardziej wierny rzeczywistości, ponieważ „zmiana” średniego wskaźnika prawdopodobnie rozciągnęłaby się na wiele lat). Nowy model jest zatem:
\[ \begin{align*} (D_t|s,e,l)&\sim\text{Poisson}(r_t), \\ & \,\quad \text{with}\; r_t = e + \frac{1}{1+\exp(s-t)}(l-e) \\ s&\sim\text{Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
W związku z brakiem dalszych informacji zakładamy \(r_e = r_l = 1\) jako parametry dla priors. Przeprowadzimy oba modele i porównamy ich wyniki wnioskowania.
def disaster_count_model(disaster_rate_fn):
disaster_count = tfd.JointDistributionNamed(dict(
e=tfd.Exponential(rate=1.),
l=tfd.Exponential(rate=1.),
s=tfd.Uniform(0., high=len(years)),
d_t=lambda s, l, e: tfd.Independent(
tfd.Poisson(rate=disaster_rate_fn(np.arange(len(years)), s, l, e)),
reinterpreted_batch_ndims=1)
))
return disaster_count
def disaster_rate_switch(ys, s, l, e):
return tf.where(ys < s, e, l)
def disaster_rate_sigmoid(ys, s, l, e):
return e + tf.sigmoid(ys - s) * (l - e)
model_switch = disaster_count_model(disaster_rate_switch)
model_sigmoid = disaster_count_model(disaster_rate_sigmoid)
Powyższy kod definiuje model za pośrednictwem dystrybucji JointDistributionSequential. W disaster_rate funkcje są wywoływane z tablicą [0, ..., len(years)-1] w celu wytworzenia wektora len(years) zmiennych losowych - lata przed switchpoint są early_disaster_rate , te po late_disaster_rate (modulo przejście esicy).
Oto kontrola poprawności, czy funkcja prob logu docelowego jest rozsądna:
def target_log_prob_fn(model, s, e, l):
return model.log_prob(s=s, e=e, l=l, d_t=disaster_data)
models = [model_switch, model_sigmoid]
print([target_log_prob_fn(m, 40., 3., .9).numpy() for m in models]) # Somewhat likely result
print([target_log_prob_fn(m, 60., 1., 5.).numpy() for m in models]) # Rather unlikely result
print([target_log_prob_fn(m, -10., 1., 1.).numpy() for m in models]) # Impossible result
[-176.94559, -176.28717] [-371.3125, -366.8816] [-inf, -inf]
HMC do wnioskowania bayesowskiego
Określamy liczbę wyników i wymaganych kroków wypalania; kod jest przeważnie wzorowane dokumentacji tfp.mcmc.HamiltonianMonteCarlo . Wykorzystuje adaptacyjny rozmiar kroku (w przeciwnym razie wynik jest bardzo wrażliwy na wybraną wartość rozmiaru kroku). Używamy wartości jeden jako stanu początkowego łańcucha.
To jednak nie jest pełna historia. Jeśli wrócisz do powyższej definicji modelu, zauważysz, że niektóre rozkłady prawdopodobieństwa nie są dobrze zdefiniowane na całej linii liczb rzeczywistych. Dlatego ograniczyć przestrzeń HMC zbada owijania jądra HMC z TransformedTransitionKernel określająca forward bijectors do przekształcania liczb rzeczywistych na domenie, że rozkład prawdopodobieństwa jest zdefiniowany (patrz komentarze w kodzie poniżej).
num_results = 10000
num_burnin_steps = 3000
@tf.function(autograph=False, jit_compile=True)
def make_chain(target_log_prob_fn):
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.05,
num_leapfrog_steps=3),
bijector=[
# The switchpoint is constrained between zero and len(years).
# Hence we supply a bijector that maps the real numbers (in a
# differentiable way) to the interval (0;len(yers))
tfb.Sigmoid(low=0., high=tf.cast(len(years), dtype=tf.float32)),
# Early and late disaster rate: The exponential distribution is
# defined on the positive real numbers
tfb.Softplus(),
tfb.Softplus(),
])
kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=int(0.8*num_burnin_steps))
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
# The three latent variables
tf.ones([], name='init_switchpoint'),
tf.ones([], name='init_early_disaster_rate'),
tf.ones([], name='init_late_disaster_rate'),
],
trace_fn=None,
kernel=kernel)
return states
switch_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_switch, *args))]
sigmoid_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_sigmoid, *args))]
switchpoint, early_disaster_rate, late_disaster_rate = zip(
switch_samples, sigmoid_samples)
Uruchom oba modele równolegle:
Wizualizuj wynik
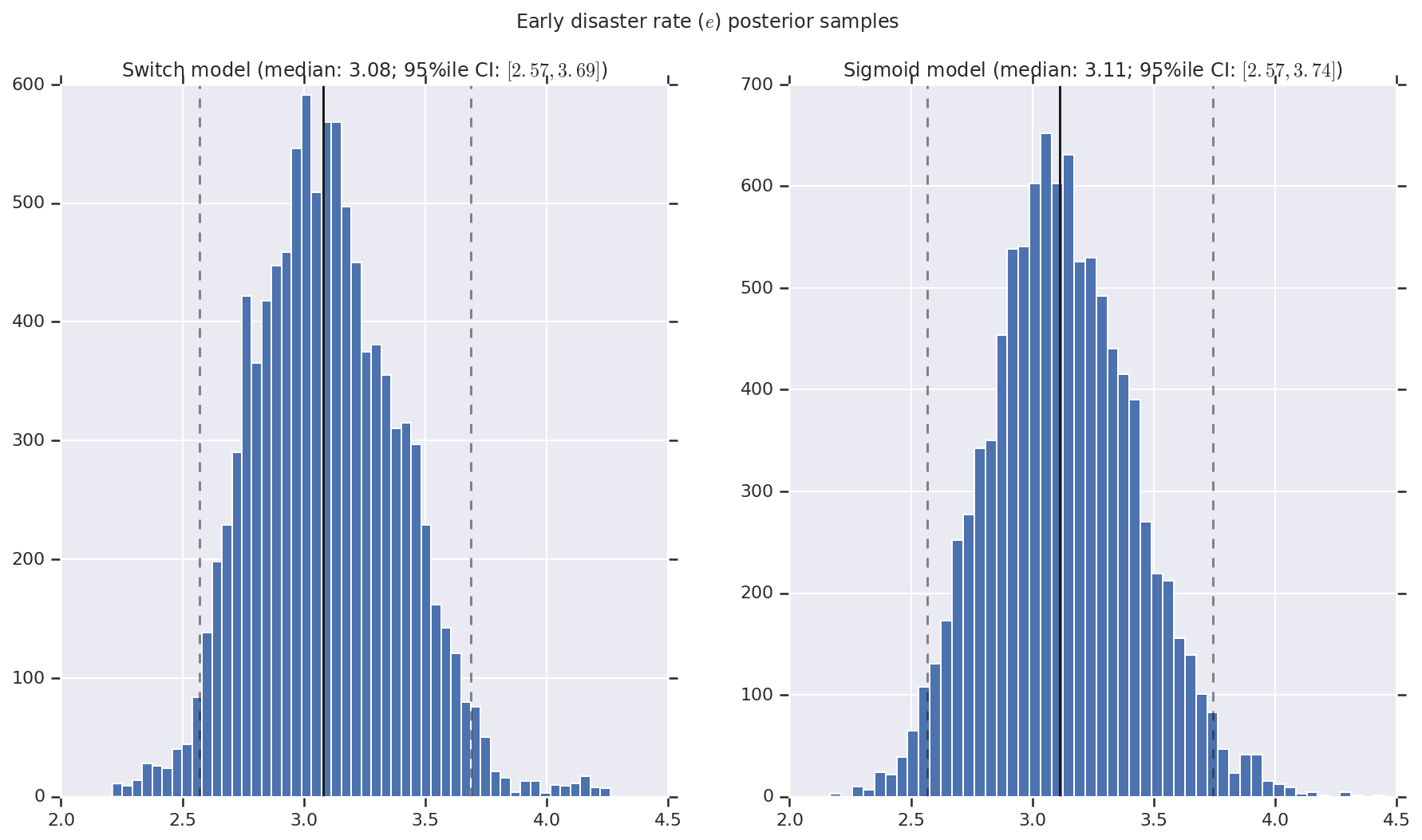
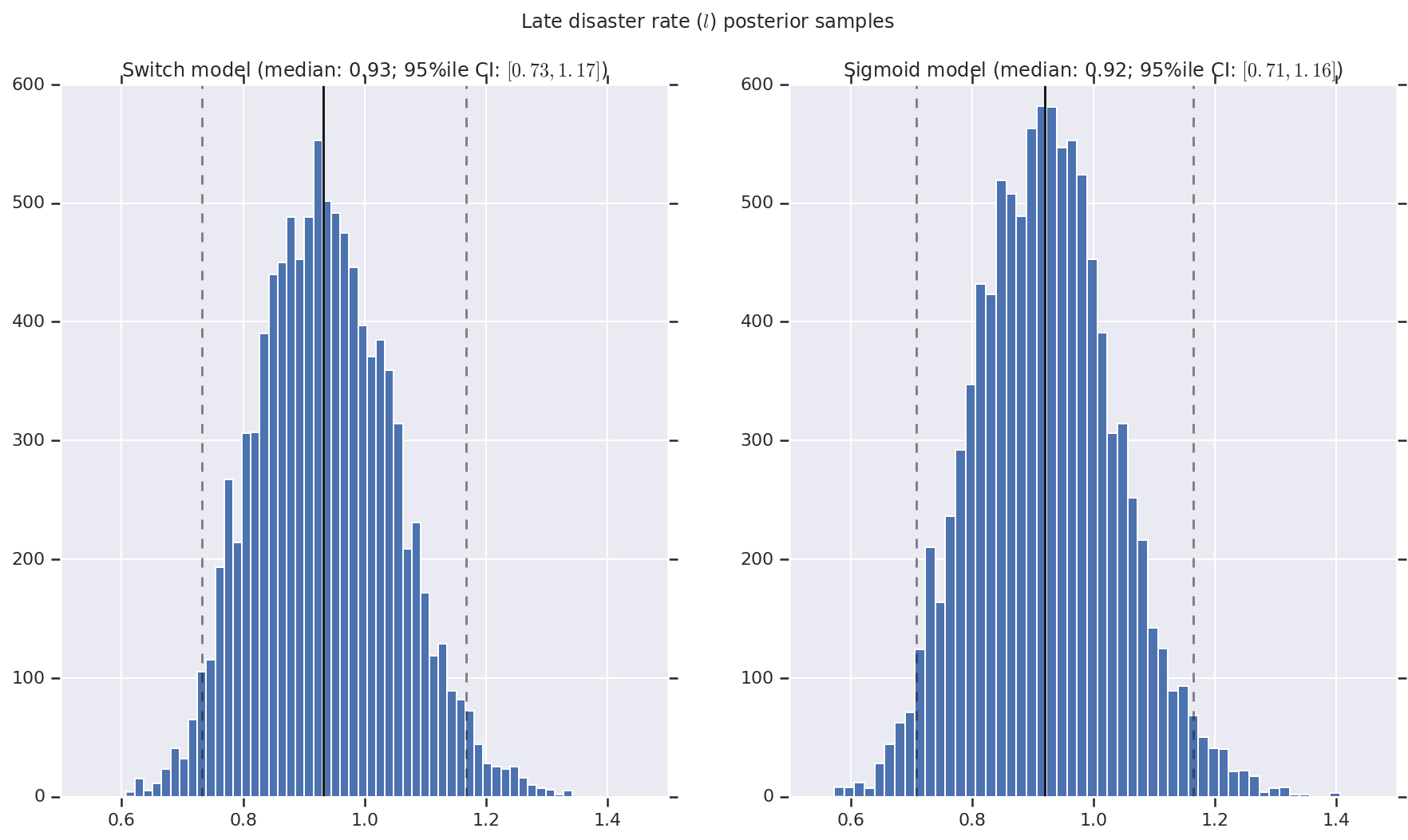
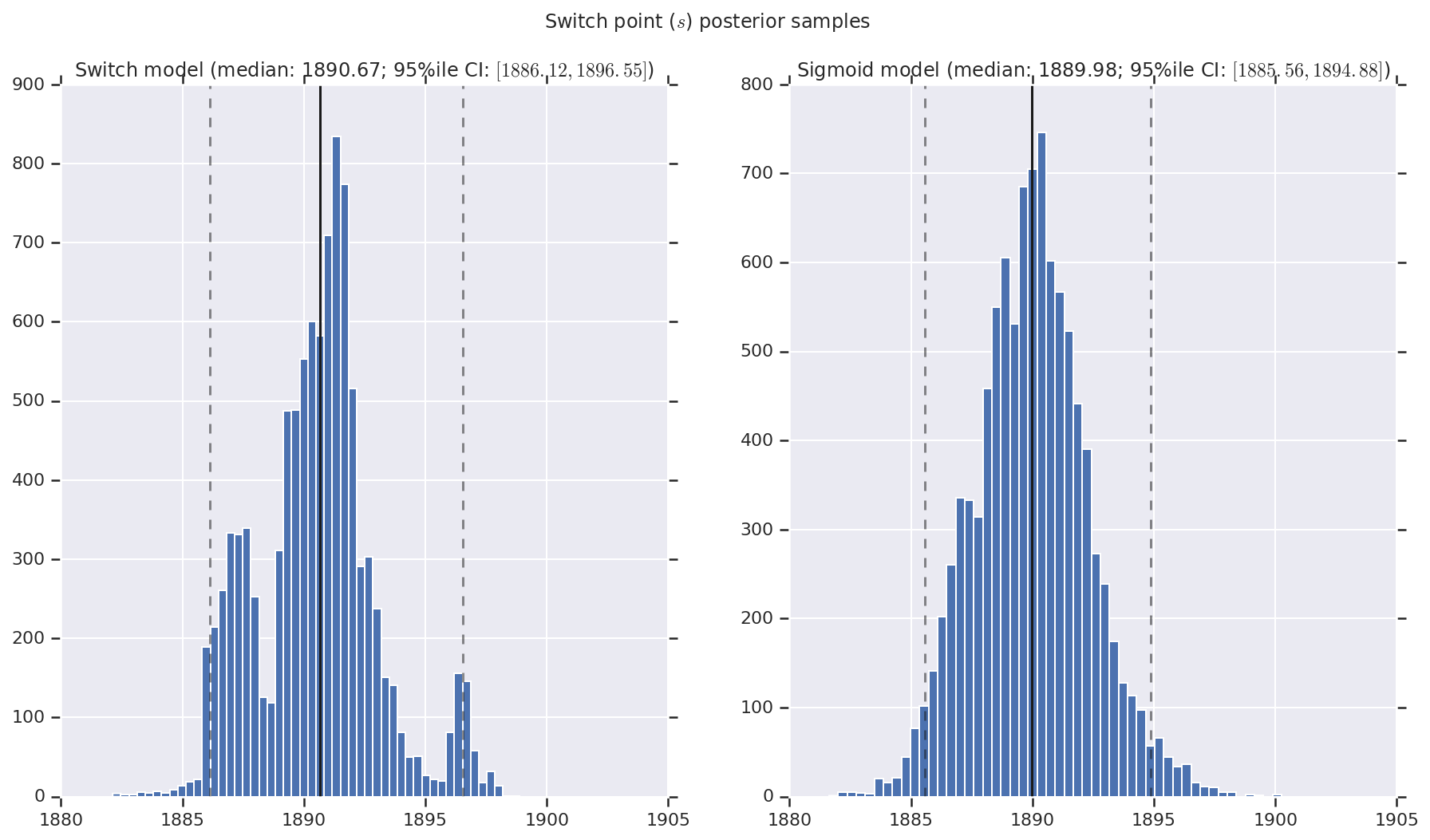
Wizualizujemy wynik jako histogramy próbek rozkładu a posteriori dla wskaźnika wczesnej i późnej katastrofy, a także punkt przełączania. Na histogramy nałożona jest linia ciągła przedstawiająca medianę próbki, a także 95% il granicy wiarygodnego przedziału jako linie przerywane.
def _desc(v):
return '(median: {}; 95%ile CI: $[{}, {}]$)'.format(
*np.round(np.percentile(v, [50, 2.5, 97.5]), 2))
for t, v in [
('Early disaster rate ($e$) posterior samples', early_disaster_rate),
('Late disaster rate ($l$) posterior samples', late_disaster_rate),
('Switch point ($s$) posterior samples', years[0] + switchpoint),
]:
fig, ax = plt.subplots(nrows=1, ncols=2, sharex=True)
for (m, i) in (('Switch', 0), ('Sigmoid', 1)):
a = ax[i]
a.hist(v[i], bins=50)
a.axvline(x=np.percentile(v[i], 50), color='k')
a.axvline(x=np.percentile(v[i], 2.5), color='k', ls='dashed', alpha=.5)
a.axvline(x=np.percentile(v[i], 97.5), color='k', ls='dashed', alpha=.5)
a.set_title(m + ' model ' + _desc(v[i]))
fig.suptitle(t)
plt.show()