Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Notebook ini reimplements dan memperluas Bayesian “Perubahan titik analisis” contoh dari dokumentasi pymc3 .
Prasyarat
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (15,8)
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
Himpunan data
Dataset adalah dari sini . Catatan, ada versi lain dari contoh ini mengambang di sekitar , tetapi telah “hilang” Data - dalam hal ini Anda akan perlu untuk menghubungkan nilai-nilai yang hilang. (Jika tidak, model Anda tidak akan pernah meninggalkan parameter awalnya karena fungsi kemungkinan tidak akan ditentukan.)
disaster_data = np.array([ 4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
2, 2, 3, 4, 2, 1, 3, 2, 2, 1, 1, 1, 1, 3, 0, 0,
1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
3, 3, 1, 1, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1])
years = np.arange(1851, 1962)
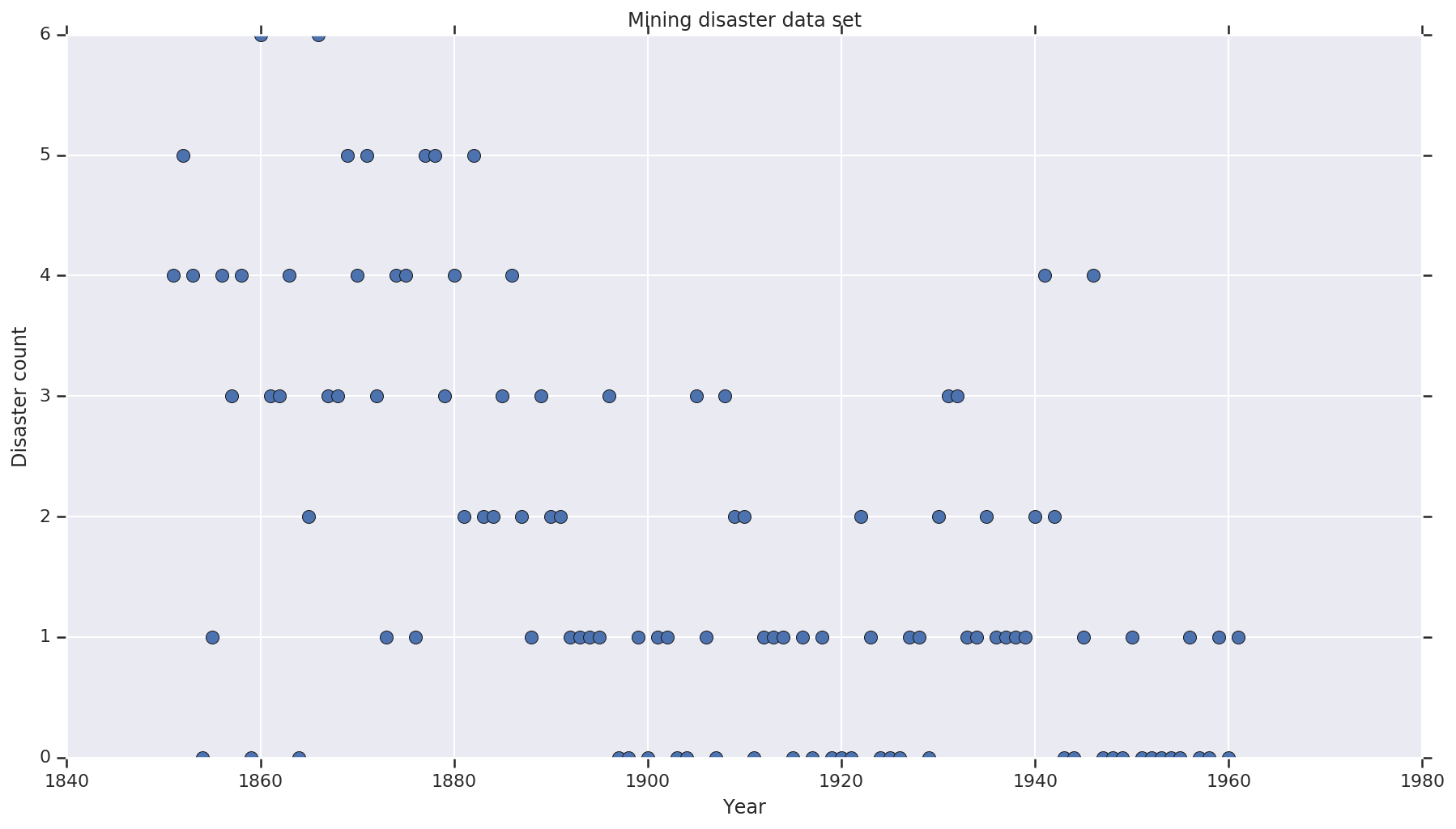
plt.plot(years, disaster_data, 'o', markersize=8);
plt.ylabel('Disaster count')
plt.xlabel('Year')
plt.title('Mining disaster data set')
plt.show()
Model Probabilistik
Model mengasumsikan sebuah “titik saklar” (misalnya satu tahun di mana peraturan keselamatan berubah), dan tingkat bencana terdistribusi Poisson dengan tingkat yang konstan (tetapi berpotensi berbeda) sebelum dan sesudah titik saklar tersebut.
Hitungan bencana yang sebenarnya adalah tetap (diamati); sampel apa pun dari model ini perlu menentukan baik titik sakelar maupun tingkat bencana "awal" dan "terlambat".
Model asli dari dokumentasi pymc3 contoh :
\[ \begin{align*} (D_t|s,e,l)&\sim \text{Poisson}(r_t), \\ & \,\quad\text{with}\; r_t = \begin{cases}e & \text{if}\; t < s\\l &\text{if}\; t \ge s\end{cases} \\ s&\sim\text{Discrete Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
Namun, rata-rata tingkat bencana \(r_t\) memiliki diskontinuitas di switchpoint \(s\), yang membuatnya tidak terdiferensiasi. Oleh karena itu tidak memberikan sinyal gradien untuk Hamiltonian Monte Carlo (HMC) algoritma - tetapi karena \(s\) sebelum kontinu, fallback HMC untuk acak berjalan cukup baik untuk menemukan daerah massa probabilitas tinggi dalam contoh ini.
Sebagai model kedua, kami memodifikasi model asli menggunakan sigmoid “switch” antara e dan l untuk membuat transisi terdiferensiasi, dan menggunakan distribusi seragam terus menerus untuk switchpoint \(s\). (Orang dapat berargumentasi bahwa model ini lebih sesuai dengan kenyataan, karena "peralihan" dalam tingkat rata-rata kemungkinan akan diperpanjang selama beberapa tahun.) Model barunya adalah:
\[ \begin{align*} (D_t|s,e,l)&\sim\text{Poisson}(r_t), \\ & \,\quad \text{with}\; r_t = e + \frac{1}{1+\exp(s-t)}(l-e) \\ s&\sim\text{Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
Dengan tidak adanya informasi lebih lanjut kita asumsikan \(r_e = r_l = 1\) sebagai parameter untuk prior. Kami akan menjalankan kedua model dan membandingkan hasil inferensi mereka.
def disaster_count_model(disaster_rate_fn):
disaster_count = tfd.JointDistributionNamed(dict(
e=tfd.Exponential(rate=1.),
l=tfd.Exponential(rate=1.),
s=tfd.Uniform(0., high=len(years)),
d_t=lambda s, l, e: tfd.Independent(
tfd.Poisson(rate=disaster_rate_fn(np.arange(len(years)), s, l, e)),
reinterpreted_batch_ndims=1)
))
return disaster_count
def disaster_rate_switch(ys, s, l, e):
return tf.where(ys < s, e, l)
def disaster_rate_sigmoid(ys, s, l, e):
return e + tf.sigmoid(ys - s) * (l - e)
model_switch = disaster_count_model(disaster_rate_switch)
model_sigmoid = disaster_count_model(disaster_rate_sigmoid)
Kode di atas mendefinisikan model melalui distribusi JointDistributionSequential. The disaster_rate fungsi disebut dengan array [0, ..., len(years)-1] untuk menghasilkan vektor len(years) variabel acak - tahun-tahun sebelum switchpoint yang early_disaster_rate , yang setelah late_disaster_rate (modulo transisi sigmoid).
Berikut adalah pemeriksaan kewarasan bahwa fungsi log prob target waras:
def target_log_prob_fn(model, s, e, l):
return model.log_prob(s=s, e=e, l=l, d_t=disaster_data)
models = [model_switch, model_sigmoid]
print([target_log_prob_fn(m, 40., 3., .9).numpy() for m in models]) # Somewhat likely result
print([target_log_prob_fn(m, 60., 1., 5.).numpy() for m in models]) # Rather unlikely result
print([target_log_prob_fn(m, -10., 1., 1.).numpy() for m in models]) # Impossible result
[-176.94559, -176.28717] [-371.3125, -366.8816] [-inf, -inf]
HMC untuk melakukan inferensi Bayesian
Kami menentukan jumlah hasil dan langkah-langkah burn-in yang diperlukan; Kode ini kebanyakan model setelah dokumentasi tfp.mcmc.HamiltonianMonteCarlo . Ini menggunakan ukuran langkah adaptif (jika tidak, hasilnya sangat sensitif terhadap nilai ukuran langkah yang dipilih). Kami menggunakan nilai satu sebagai keadaan awal rantai.
Ini bukan cerita lengkapnya. Jika Anda kembali ke definisi model di atas, Anda akan melihat bahwa beberapa distribusi probabilitas tidak terdefinisi dengan baik pada seluruh garis bilangan real. Oleh karena itu kami membatasi ruang yang HMC harus memeriksa dengan membungkus kernel HMC dengan TransformedTransitionKernel yang menentukan bijectors depan untuk mengubah bilangan real ke domain bahwa distribusi probabilitas didefinisikan pada (lihat komentar dalam kode di bawah).
num_results = 10000
num_burnin_steps = 3000
@tf.function(autograph=False, jit_compile=True)
def make_chain(target_log_prob_fn):
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.05,
num_leapfrog_steps=3),
bijector=[
# The switchpoint is constrained between zero and len(years).
# Hence we supply a bijector that maps the real numbers (in a
# differentiable way) to the interval (0;len(yers))
tfb.Sigmoid(low=0., high=tf.cast(len(years), dtype=tf.float32)),
# Early and late disaster rate: The exponential distribution is
# defined on the positive real numbers
tfb.Softplus(),
tfb.Softplus(),
])
kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=int(0.8*num_burnin_steps))
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
# The three latent variables
tf.ones([], name='init_switchpoint'),
tf.ones([], name='init_early_disaster_rate'),
tf.ones([], name='init_late_disaster_rate'),
],
trace_fn=None,
kernel=kernel)
return states
switch_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_switch, *args))]
sigmoid_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_sigmoid, *args))]
switchpoint, early_disaster_rate, late_disaster_rate = zip(
switch_samples, sigmoid_samples)
Jalankan kedua model secara paralel:
Visualisasikan hasilnya
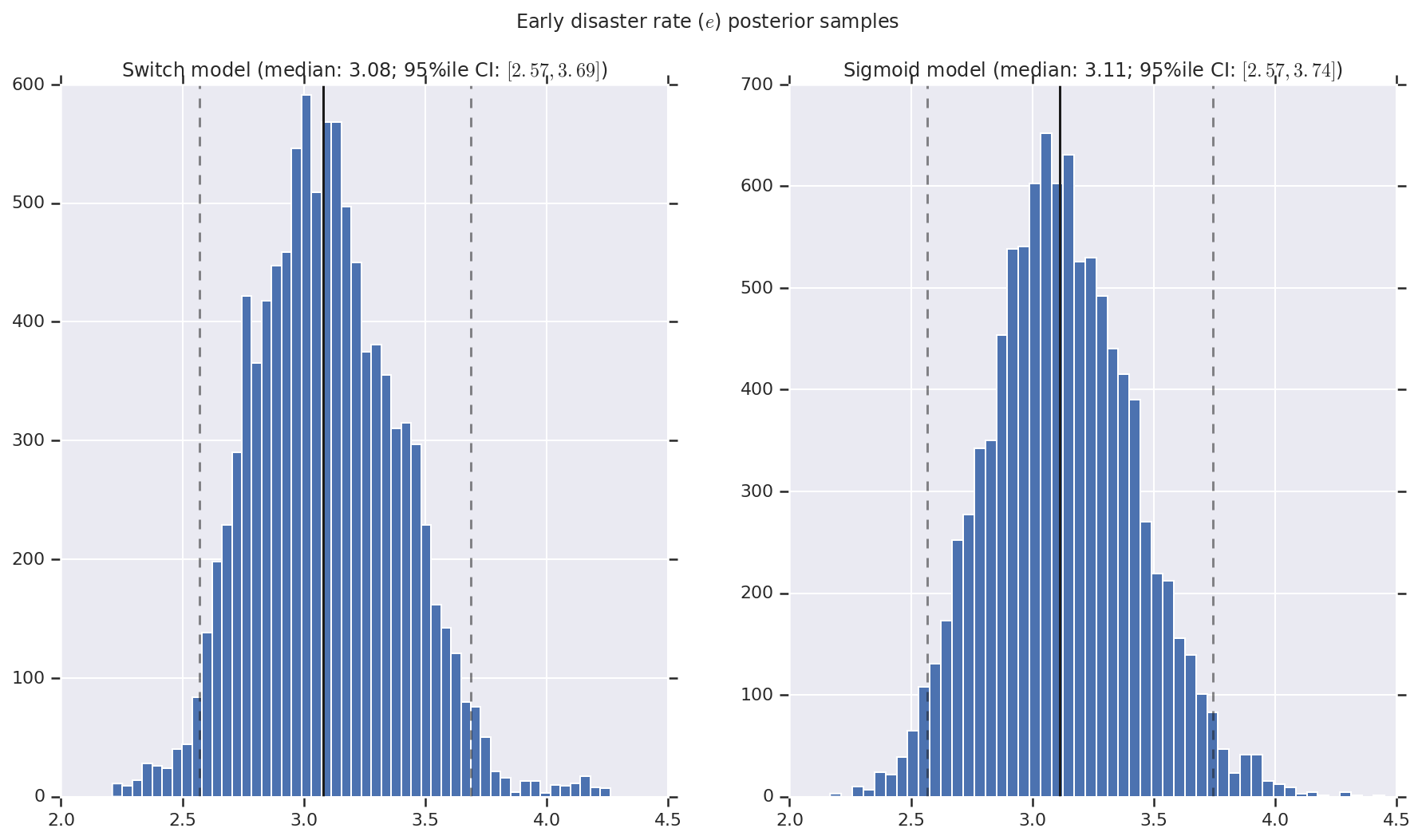
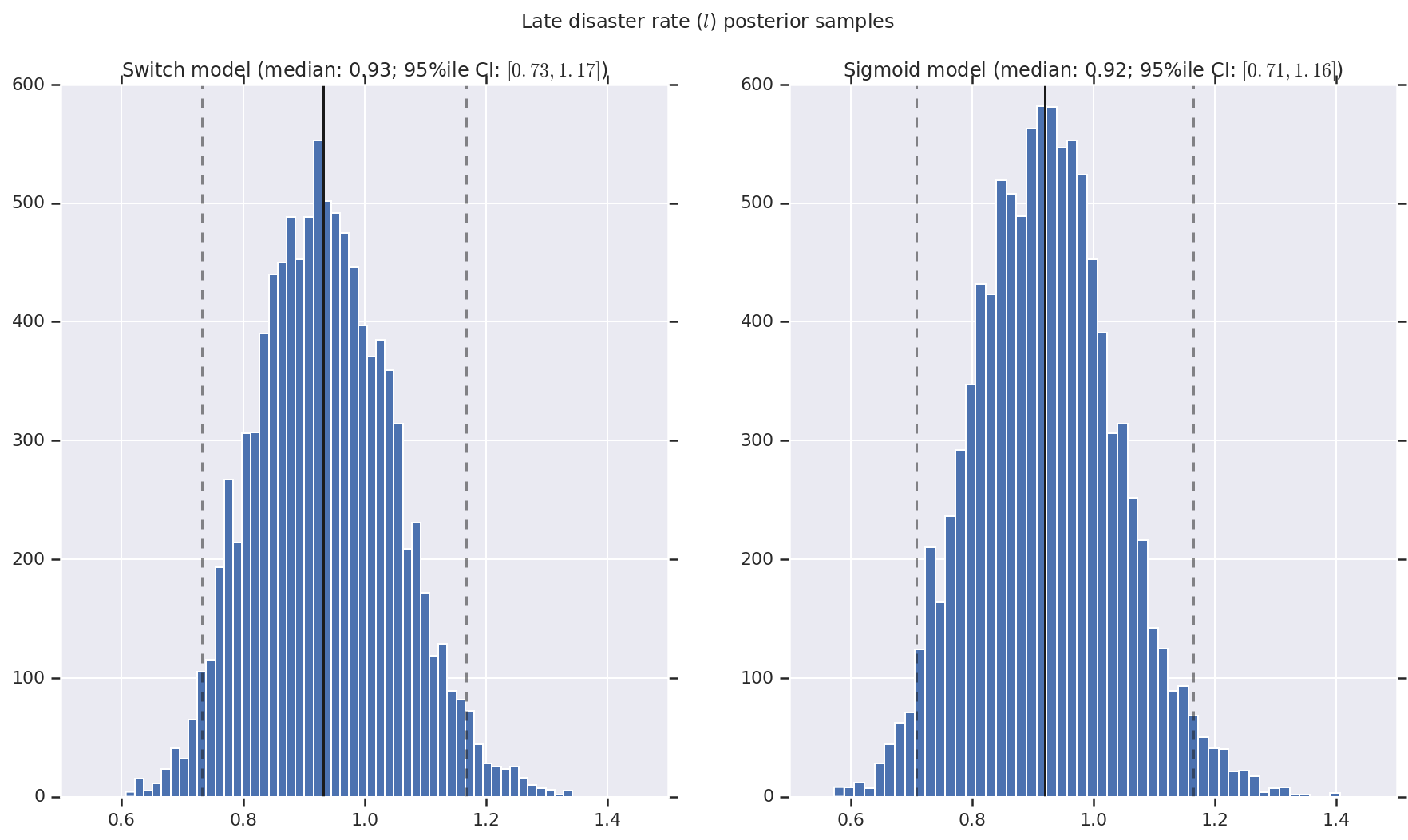
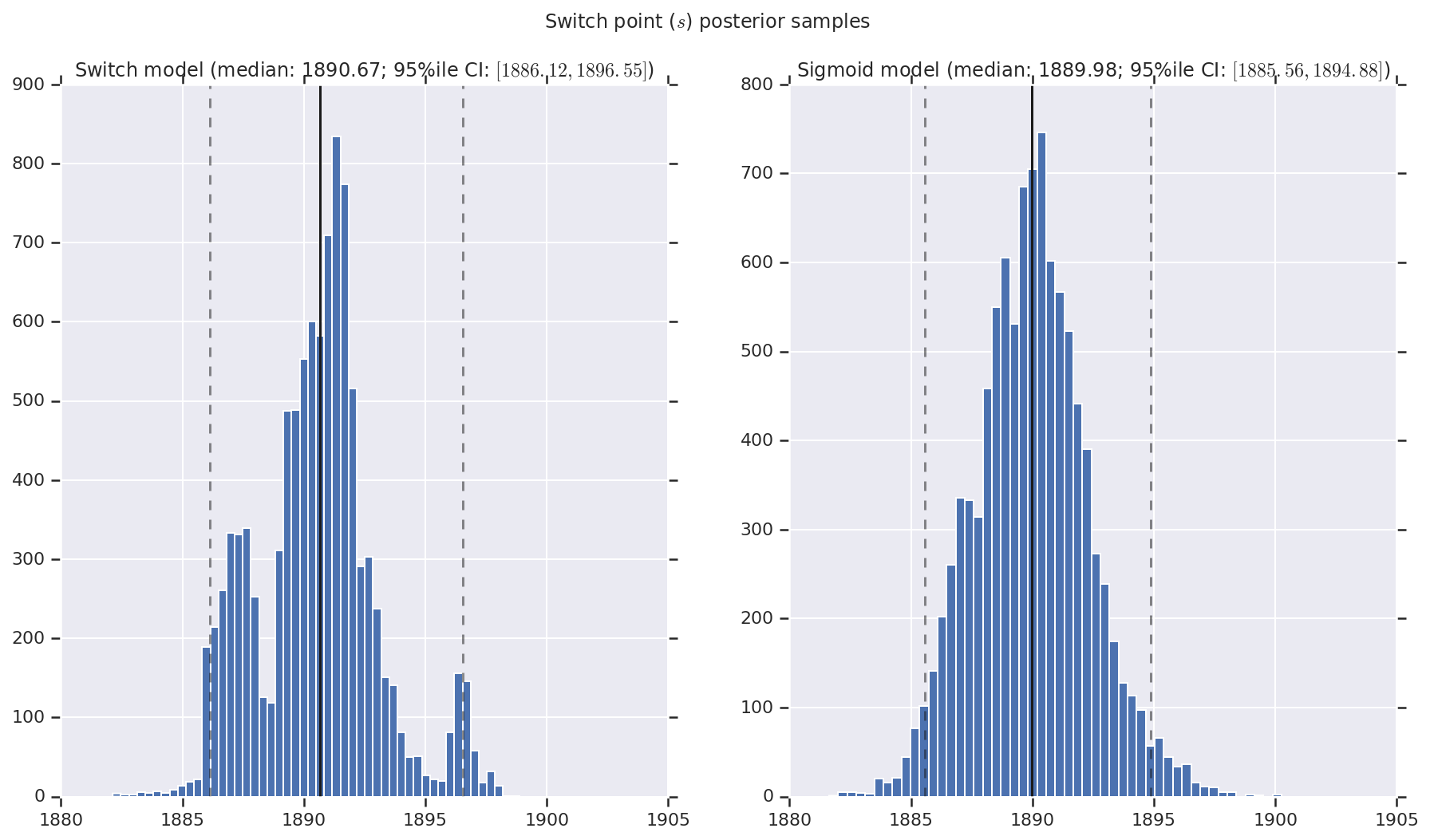
Kami memvisualisasikan hasilnya sebagai histogram sampel distribusi posterior untuk tingkat bencana awal dan akhir, serta titik peralihan. Histogram dilapis dengan garis padat yang mewakili median sampel, serta batas interval kredibel 95% sebagai garis putus-putus.
def _desc(v):
return '(median: {}; 95%ile CI: $[{}, {}]$)'.format(
*np.round(np.percentile(v, [50, 2.5, 97.5]), 2))
for t, v in [
('Early disaster rate ($e$) posterior samples', early_disaster_rate),
('Late disaster rate ($l$) posterior samples', late_disaster_rate),
('Switch point ($s$) posterior samples', years[0] + switchpoint),
]:
fig, ax = plt.subplots(nrows=1, ncols=2, sharex=True)
for (m, i) in (('Switch', 0), ('Sigmoid', 1)):
a = ax[i]
a.hist(v[i], bins=50)
a.axvline(x=np.percentile(v[i], 50), color='k')
a.axvline(x=np.percentile(v[i], 2.5), color='k', ls='dashed', alpha=.5)
a.axvline(x=np.percentile(v[i], 97.5), color='k', ls='dashed', alpha=.5)
a.set_title(m + ' model ' + _desc(v[i]))
fig.suptitle(t)
plt.show()