مشاهده در TensorFlow.org مشاهده در TensorFlow.org |  در Google Colab اجرا شود در Google Colab اجرا شود |  مشاهده منبع در GitHub مشاهده منبع در GitHub |  دانلود دفترچه یادداشت دانلود دفترچه یادداشت |
این reimplements نوت بوک و "تجزیه و تحلیل نقطه تغییر" بیزی به عنوان مثال از گسترش مستندات pymc3 .
پیش نیازها
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (15,8)
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
مجموعه داده
مجموعه داده از است در اینجا . توجه داشته باشید، نسخه دیگری از این مثال وجود دارد شناور در اطراف ، اما آن را "از دست رفته" داده ها - که در این صورت شما می باید نسبت دادن مقادیر از دست رفته. (در غیر این صورت مدل شما هرگز پارامترهای اولیه خود را ترک نخواهد کرد زیرا تابع احتمال تعریف نشده است.)
disaster_data = np.array([ 4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
2, 2, 3, 4, 2, 1, 3, 2, 2, 1, 1, 1, 1, 3, 0, 0,
1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
3, 3, 1, 1, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1])
years = np.arange(1851, 1962)
plt.plot(years, disaster_data, 'o', markersize=8);
plt.ylabel('Disaster count')
plt.xlabel('Year')
plt.title('Mining disaster data set')
plt.show()
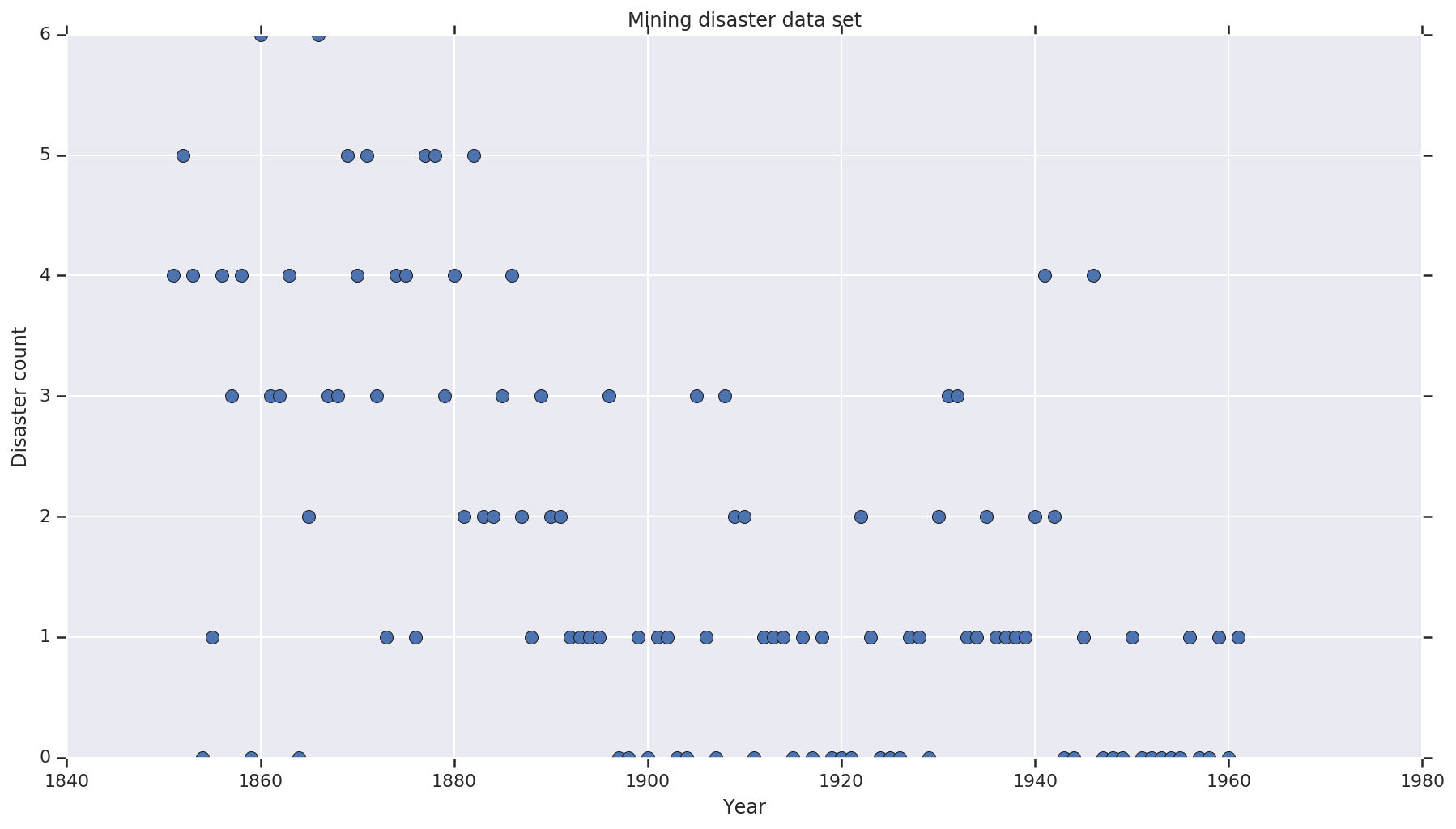
مدل احتمالی
این مدل یک "نقطه سوئیچ" (به عنوان مثال سالی که در طی آن مقررات ایمنی تغییر کرد) و نرخ فاجعه توزیع شده توسط پواسون با نرخ های ثابت (اما بالقوه متفاوت) قبل و بعد از آن نقطه سوئیچ را در نظر می گیرد.
شمارش واقعی فاجعه ثابت است (مشاهده)؛ هر نمونه ای از این مدل باید هم نقطه سوئیچ و هم نرخ "زود" و "دیر" بلایا را مشخص کند.
مدل اصلی از مثال مستندات pymc3 :
\[ \begin{align*} (D_t|s,e,l)&\sim \text{Poisson}(r_t), \\ & \,\quad\text{with}\; r_t = \begin{cases}e & \text{if}\; t < s\\l &\text{if}\; t \ge s\end{cases} \\ s&\sim\text{Discrete Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
با این حال، میانگین نرخ فاجعه \(r_t\) است ناپیوستگی در switchpoint \(s\)، که آن را مشتق پذیر نیست. بنابراین آن را فراهم می کند که هیچ سیگنال شیب به (HMC) الگوریتم هامیلتونی مونت کارلو - اما به دلیل \(s\) قبل پیوسته است، مجدد شورای عالی رسانه ها را به یک پیاده روی تصادفی به اندازه کافی خوب برای پیدا کردن زمینه های جرم احتمال بالا در این مثال است.
به عنوان یک مدل دوم، ما از مدل اصلی با استفاده از یک تغییر سیگموئید "سوئیچ" بین E و l به انتقال مشتقپذیر، و استفاده از یک توزیع یکنواخت پیوسته برای switchpoint \(s\). (کسی میتواند استدلال کند که این مدل بیشتر با واقعیت صادق است، زیرا یک "تغییر" در نرخ متوسط احتمالاً در طی چندین سال طولانی خواهد شد.) مدل جدید بدین ترتیب است:
\[ \begin{align*} (D_t|s,e,l)&\sim\text{Poisson}(r_t), \\ & \,\quad \text{with}\; r_t = e + \frac{1}{1+\exp(s-t)}(l-e) \\ s&\sim\text{Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
در صورت عدم وجود اطلاعات بیشتر ما فرض \(r_e = r_l = 1\) عنوان پارامتر به priors. ما هر دو مدل را اجرا می کنیم و نتایج استنتاج آنها را با هم مقایسه می کنیم.
def disaster_count_model(disaster_rate_fn):
disaster_count = tfd.JointDistributionNamed(dict(
e=tfd.Exponential(rate=1.),
l=tfd.Exponential(rate=1.),
s=tfd.Uniform(0., high=len(years)),
d_t=lambda s, l, e: tfd.Independent(
tfd.Poisson(rate=disaster_rate_fn(np.arange(len(years)), s, l, e)),
reinterpreted_batch_ndims=1)
))
return disaster_count
def disaster_rate_switch(ys, s, l, e):
return tf.where(ys < s, e, l)
def disaster_rate_sigmoid(ys, s, l, e):
return e + tf.sigmoid(ys - s) * (l - e)
model_switch = disaster_count_model(disaster_rate_switch)
model_sigmoid = disaster_count_model(disaster_rate_sigmoid)
کد بالا مدل را از طریق توزیع های JointDistributionSequential تعریف می کند. disaster_rate توابع با آرایه ای از نام [0, ..., len(years)-1] برای تولید یک بردار len(years) متغیرهای تصادفی - سال های پیش از switchpoint هستند early_disaster_rate ، آنهایی که پس از late_disaster_rate (پیمانه انتقال سیگموئید).
در اینجا یک بررسی عاقلانه وجود دارد که آیا تابع log target prob سالم است:
def target_log_prob_fn(model, s, e, l):
return model.log_prob(s=s, e=e, l=l, d_t=disaster_data)
models = [model_switch, model_sigmoid]
print([target_log_prob_fn(m, 40., 3., .9).numpy() for m in models]) # Somewhat likely result
print([target_log_prob_fn(m, 60., 1., 5.).numpy() for m in models]) # Rather unlikely result
print([target_log_prob_fn(m, -10., 1., 1.).numpy() for m in models]) # Impossible result
[-176.94559, -176.28717] [-371.3125, -366.8816] [-inf, -inf]
HMC برای انجام استنتاج بیزی
ما تعداد نتایج و مراحل رایت در مورد نیاز را تعریف می کنیم. کد عمدتا پس از مدل سازی اسناد از tfp.mcmc.HamiltonianMonteCarlo . از یک اندازه گام تطبیقی استفاده می کند (در غیر این صورت نتیجه به مقدار اندازه مرحله انتخاب شده بسیار حساس است). ما از مقادیر یک به عنوان حالت اولیه زنجیره استفاده می کنیم.
اگرچه این داستان کامل نیست. اگر به تعریف مدل بالا برگردید، متوجه خواهید شد که برخی از توزیعهای احتمال در کل خط اعداد واقعی به خوبی تعریف نشدهاند. بنابراین ما فضا است که شورای عالی رسانه ها باید با کاغذ بسته بندی هسته HMC با بررسی محدود TransformedTransitionKernel که را مشخص bijectors رو به جلو برای تبدیل اعداد حقیقی بر روی دامنه ای که توزیع احتمال بر تعریف (نظرات در کد زیر را ببینید).
num_results = 10000
num_burnin_steps = 3000
@tf.function(autograph=False, jit_compile=True)
def make_chain(target_log_prob_fn):
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.05,
num_leapfrog_steps=3),
bijector=[
# The switchpoint is constrained between zero and len(years).
# Hence we supply a bijector that maps the real numbers (in a
# differentiable way) to the interval (0;len(yers))
tfb.Sigmoid(low=0., high=tf.cast(len(years), dtype=tf.float32)),
# Early and late disaster rate: The exponential distribution is
# defined on the positive real numbers
tfb.Softplus(),
tfb.Softplus(),
])
kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=int(0.8*num_burnin_steps))
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
# The three latent variables
tf.ones([], name='init_switchpoint'),
tf.ones([], name='init_early_disaster_rate'),
tf.ones([], name='init_late_disaster_rate'),
],
trace_fn=None,
kernel=kernel)
return states
switch_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_switch, *args))]
sigmoid_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_sigmoid, *args))]
switchpoint, early_disaster_rate, late_disaster_rate = zip(
switch_samples, sigmoid_samples)
هر دو مدل را به صورت موازی اجرا کنید:
نتیجه را تجسم کنید
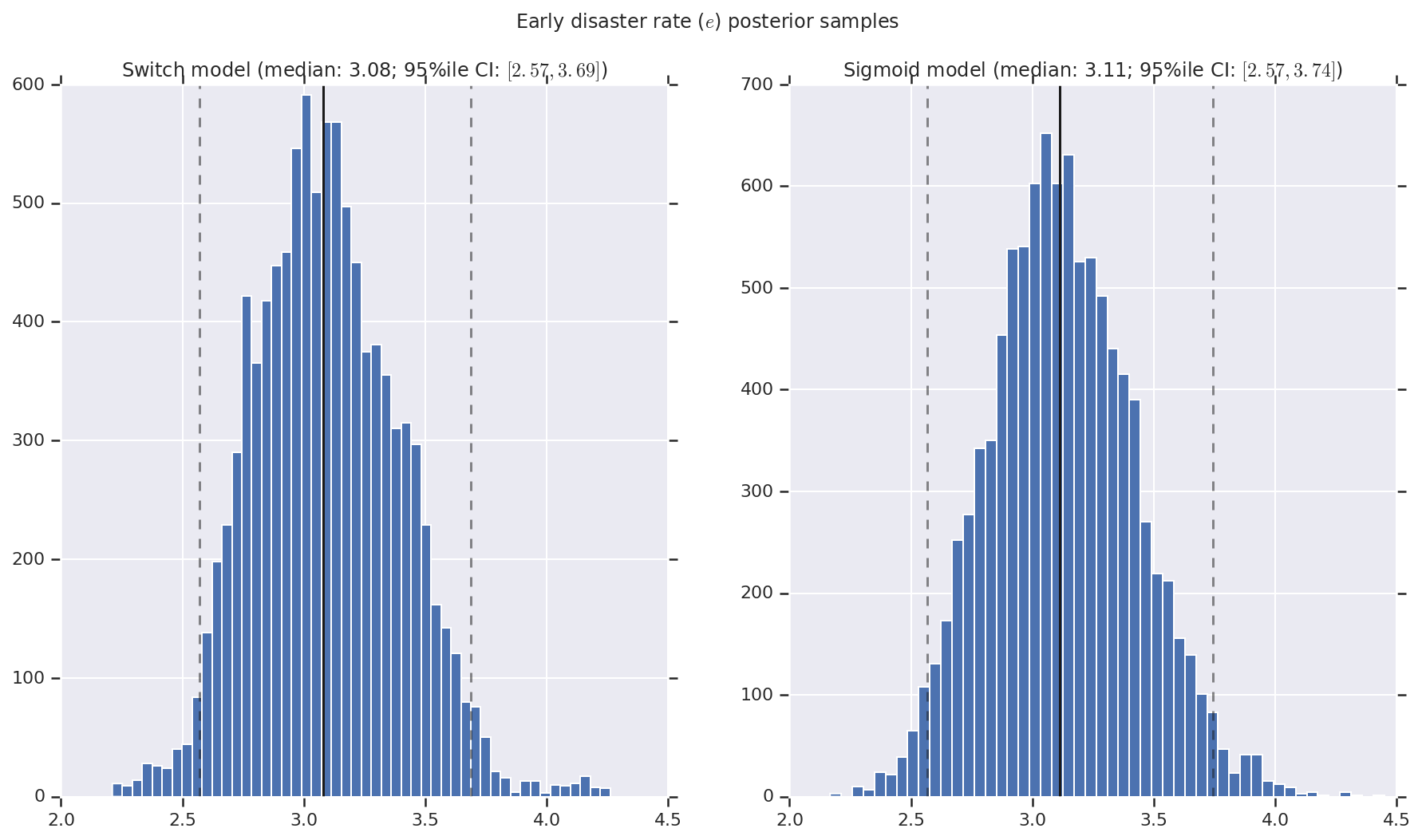
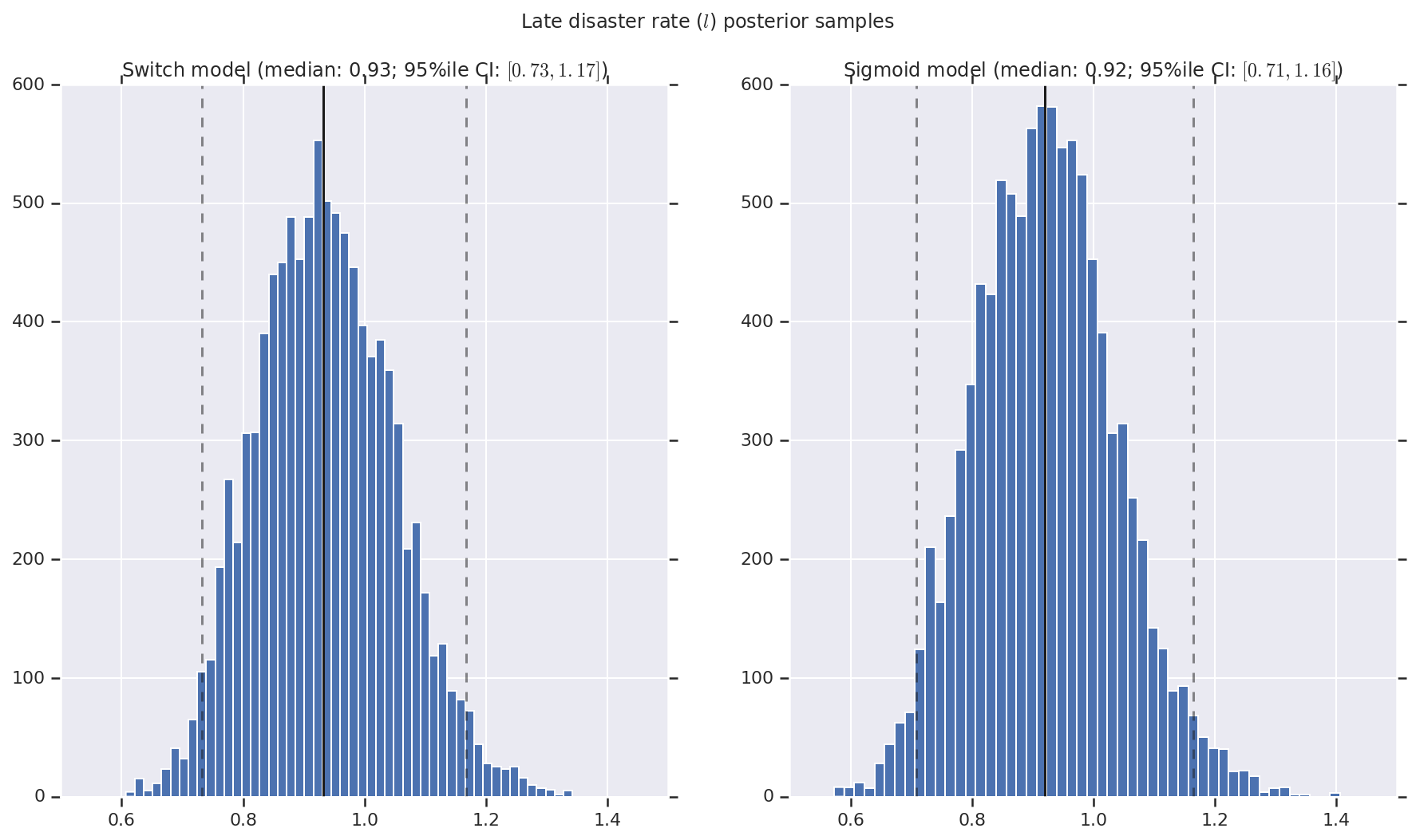
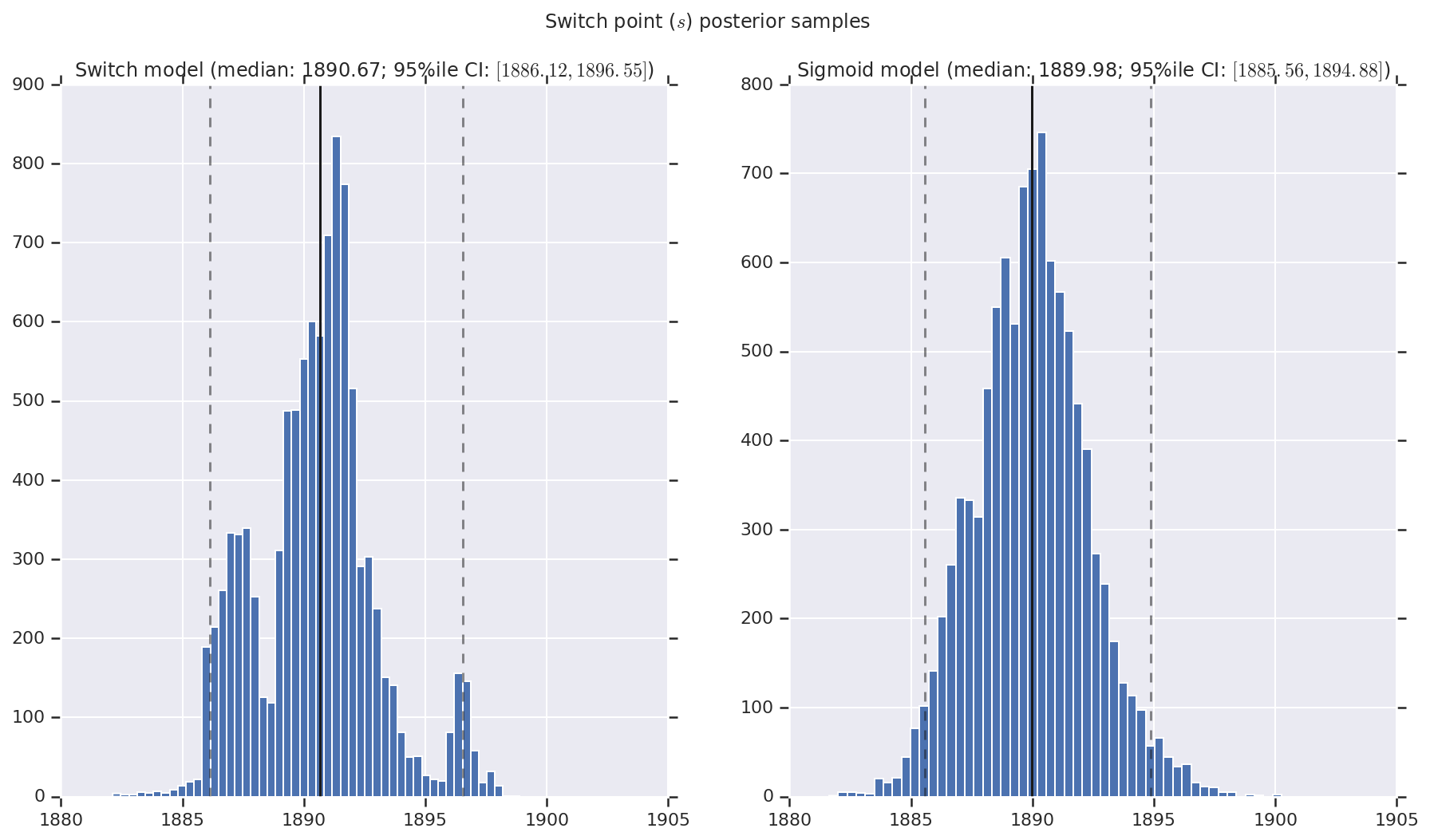
ما نتیجه را بهعنوان هیستوگرامهایی از نمونههای توزیع پسین برای نرخ فاجعه اولیه و دیررس و همچنین نقطه سوئیچ تجسم میکنیم. هیستوگرام ها با یک خط جامد که نشان دهنده میانه نمونه است، و همچنین مرزهای بازه معتبر 95% به صورت خطوط چین پوشیده شده اند.
def _desc(v):
return '(median: {}; 95%ile CI: $[{}, {}]$)'.format(
*np.round(np.percentile(v, [50, 2.5, 97.5]), 2))
for t, v in [
('Early disaster rate ($e$) posterior samples', early_disaster_rate),
('Late disaster rate ($l$) posterior samples', late_disaster_rate),
('Switch point ($s$) posterior samples', years[0] + switchpoint),
]:
fig, ax = plt.subplots(nrows=1, ncols=2, sharex=True)
for (m, i) in (('Switch', 0), ('Sigmoid', 1)):
a = ax[i]
a.hist(v[i], bins=50)
a.axvline(x=np.percentile(v[i], 50), color='k')
a.axvline(x=np.percentile(v[i], 2.5), color='k', ls='dashed', alpha=.5)
a.axvline(x=np.percentile(v[i], 97.5), color='k', ls='dashed', alpha=.5)
a.set_title(m + ' model ' + _desc(v[i]))
fig.suptitle(t)
plt.show()