Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
Este cuaderno reimplementa y extiende el “análisis de punto de cambio” Bayesiano ejemplo a partir de la documentación pymc3 .
Prerrequisitos
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (15,8)
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
Conjunto de datos
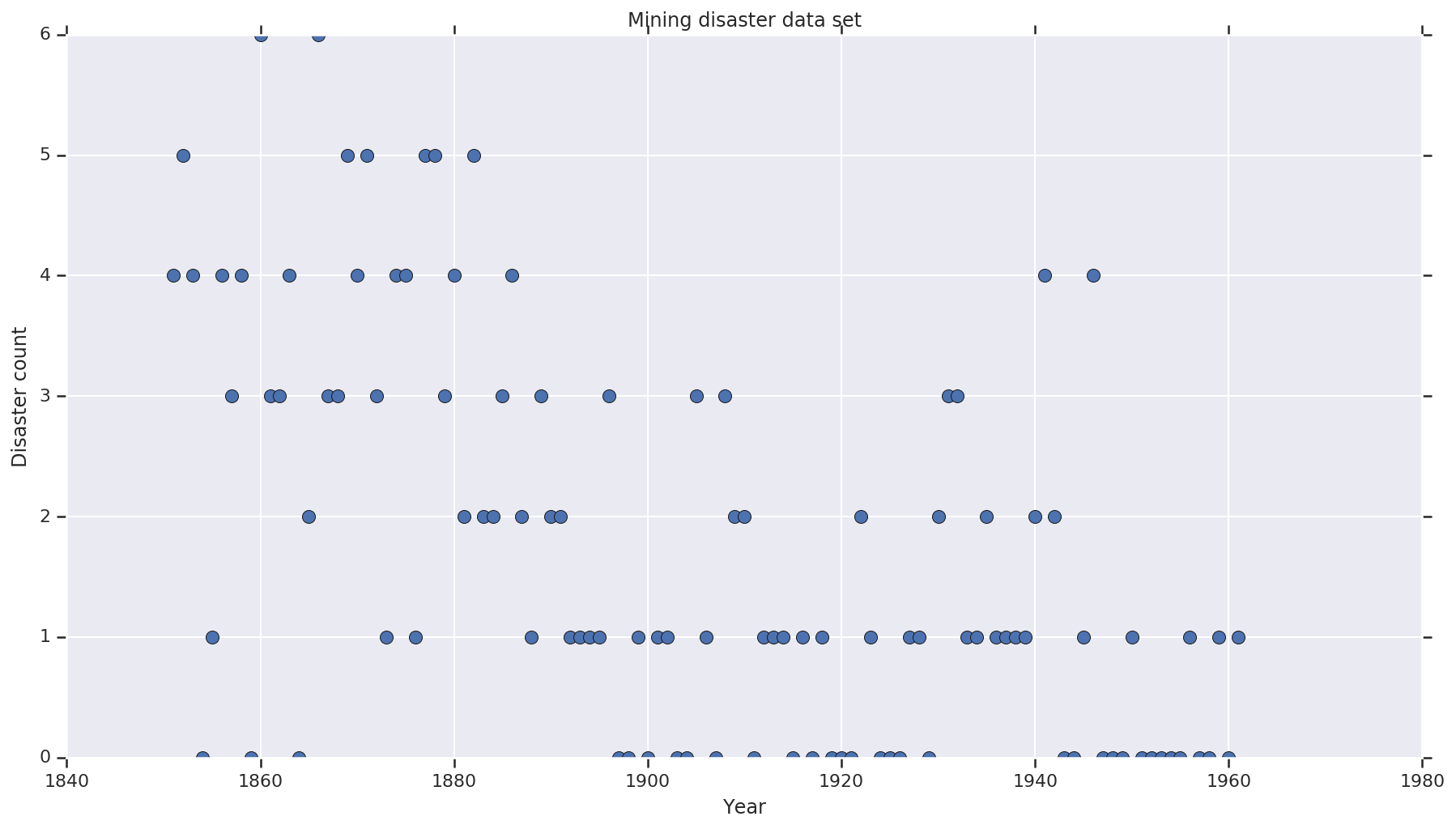
El conjunto de datos es de aquí . Nota, hay otra versión de este ejemplo flotando alrededor , pero se ha “perdido” de datos - en cuyo caso se necesitaría para imputar los valores perdidos. (De lo contrario, su modelo nunca dejará sus parámetros iniciales porque la función de probabilidad no estará definida).
disaster_data = np.array([ 4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
2, 2, 3, 4, 2, 1, 3, 2, 2, 1, 1, 1, 1, 3, 0, 0,
1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
3, 3, 1, 1, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1])
years = np.arange(1851, 1962)
plt.plot(years, disaster_data, 'o', markersize=8);
plt.ylabel('Disaster count')
plt.xlabel('Year')
plt.title('Mining disaster data set')
plt.show()
Modelo probabilístico
El modelo asume un “punto de conmutación” (por ejemplo, un año durante el cual cambiaron las normas de seguridad) y una tasa de desastre distribuida por Poisson con tasas constantes (pero potencialmente diferentes) antes y después de ese punto de conmutación.
El recuento real de desastres es fijo (observado); cualquier muestra de este modelo deberá especificar tanto el punto de conmutación como la tasa de desastres "temprana" y "tardía".
Modelo original del ejemplo pymc3 documentación :
\[ \begin{align*} (D_t|s,e,l)&\sim \text{Poisson}(r_t), \\ & \,\quad\text{with}\; r_t = \begin{cases}e & \text{if}\; t < s\\l &\text{if}\; t \ge s\end{cases} \\ s&\sim\text{Discrete Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
Sin embargo, la tasa media de desastres \(r_t\) tiene una discontinuidad en el punto de conmutación \(s\), lo que hace que no sea diferenciable. Por lo tanto, no proporciona ninguna señal de gradientes con el algoritmo de Hamilton Monte Carlo (HMC) - sino porque el \(s\) previo es continua, de repliegue de HMC con un paseo aleatorio es lo suficientemente bueno para encontrar las áreas de masas de alta probabilidad en este ejemplo.
Como un segundo modelo, modificamos el modelo original utilizando un “interruptor” sigmoide entre E y L para hacer la transición diferenciable, y el uso de una distribución uniforme continua para el punto de conmutación \(s\). (Se podría argumentar que este modelo es más fiel a la realidad, ya que un "cambio" en la tasa media probablemente se prolongaría durante varios años). El nuevo modelo es así:
\[ \begin{align*} (D_t|s,e,l)&\sim\text{Poisson}(r_t), \\ & \,\quad \text{with}\; r_t = e + \frac{1}{1+\exp(s-t)}(l-e) \\ s&\sim\text{Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
A falta de más información asumimos \(r_e = r_l = 1\) como parámetros para los priores. Ejecutaremos ambos modelos y compararemos sus resultados de inferencia.
def disaster_count_model(disaster_rate_fn):
disaster_count = tfd.JointDistributionNamed(dict(
e=tfd.Exponential(rate=1.),
l=tfd.Exponential(rate=1.),
s=tfd.Uniform(0., high=len(years)),
d_t=lambda s, l, e: tfd.Independent(
tfd.Poisson(rate=disaster_rate_fn(np.arange(len(years)), s, l, e)),
reinterpreted_batch_ndims=1)
))
return disaster_count
def disaster_rate_switch(ys, s, l, e):
return tf.where(ys < s, e, l)
def disaster_rate_sigmoid(ys, s, l, e):
return e + tf.sigmoid(ys - s) * (l - e)
model_switch = disaster_count_model(disaster_rate_switch)
model_sigmoid = disaster_count_model(disaster_rate_sigmoid)
El código anterior define el modelo a través de distribuciones JointDistributionSequential. Los disaster_rate funciones se denominan con una variedad de [0, ..., len(years)-1] para producir un vector de len(years) variables aleatorias - los años antes del switchpoint son early_disaster_rate , los queridos después late_disaster_rate (módulo el transición sigmoidea).
Aquí hay una verificación de cordura de que la función de problema de registro de destino es sensata:
def target_log_prob_fn(model, s, e, l):
return model.log_prob(s=s, e=e, l=l, d_t=disaster_data)
models = [model_switch, model_sigmoid]
print([target_log_prob_fn(m, 40., 3., .9).numpy() for m in models]) # Somewhat likely result
print([target_log_prob_fn(m, 60., 1., 5.).numpy() for m in models]) # Rather unlikely result
print([target_log_prob_fn(m, -10., 1., 1.).numpy() for m in models]) # Impossible result
[-176.94559, -176.28717] [-371.3125, -366.8816] [-inf, -inf]
HMC para hacer inferencia bayesiana
Definimos el número de resultados y los pasos necesarios; el código se modela sobre todo después de la documentación de tfp.mcmc.HamiltonianMonteCarlo . Utiliza un tamaño de paso adaptativo (de lo contrario, el resultado es muy sensible al valor de tamaño de paso elegido). Usamos valores de uno como estado inicial de la cadena.
Sin embargo, esta no es la historia completa. Si vuelve a la definición del modelo anterior, notará que algunas de las distribuciones de probabilidad no están bien definidas en toda la recta numérica real. Por lo tanto, limitan el espacio que HMC examinará envolviendo el núcleo HMC con un TransformedTransitionKernel que especifica el bijectors hacia adelante para transformar los números reales en el dominio que la distribución de probabilidad se define en (ver comentarios en el código de abajo).
num_results = 10000
num_burnin_steps = 3000
@tf.function(autograph=False, jit_compile=True)
def make_chain(target_log_prob_fn):
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.05,
num_leapfrog_steps=3),
bijector=[
# The switchpoint is constrained between zero and len(years).
# Hence we supply a bijector that maps the real numbers (in a
# differentiable way) to the interval (0;len(yers))
tfb.Sigmoid(low=0., high=tf.cast(len(years), dtype=tf.float32)),
# Early and late disaster rate: The exponential distribution is
# defined on the positive real numbers
tfb.Softplus(),
tfb.Softplus(),
])
kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=int(0.8*num_burnin_steps))
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
# The three latent variables
tf.ones([], name='init_switchpoint'),
tf.ones([], name='init_early_disaster_rate'),
tf.ones([], name='init_late_disaster_rate'),
],
trace_fn=None,
kernel=kernel)
return states
switch_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_switch, *args))]
sigmoid_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_sigmoid, *args))]
switchpoint, early_disaster_rate, late_disaster_rate = zip(
switch_samples, sigmoid_samples)
Ejecute ambos modelos en paralelo:
Visualiza el resultado
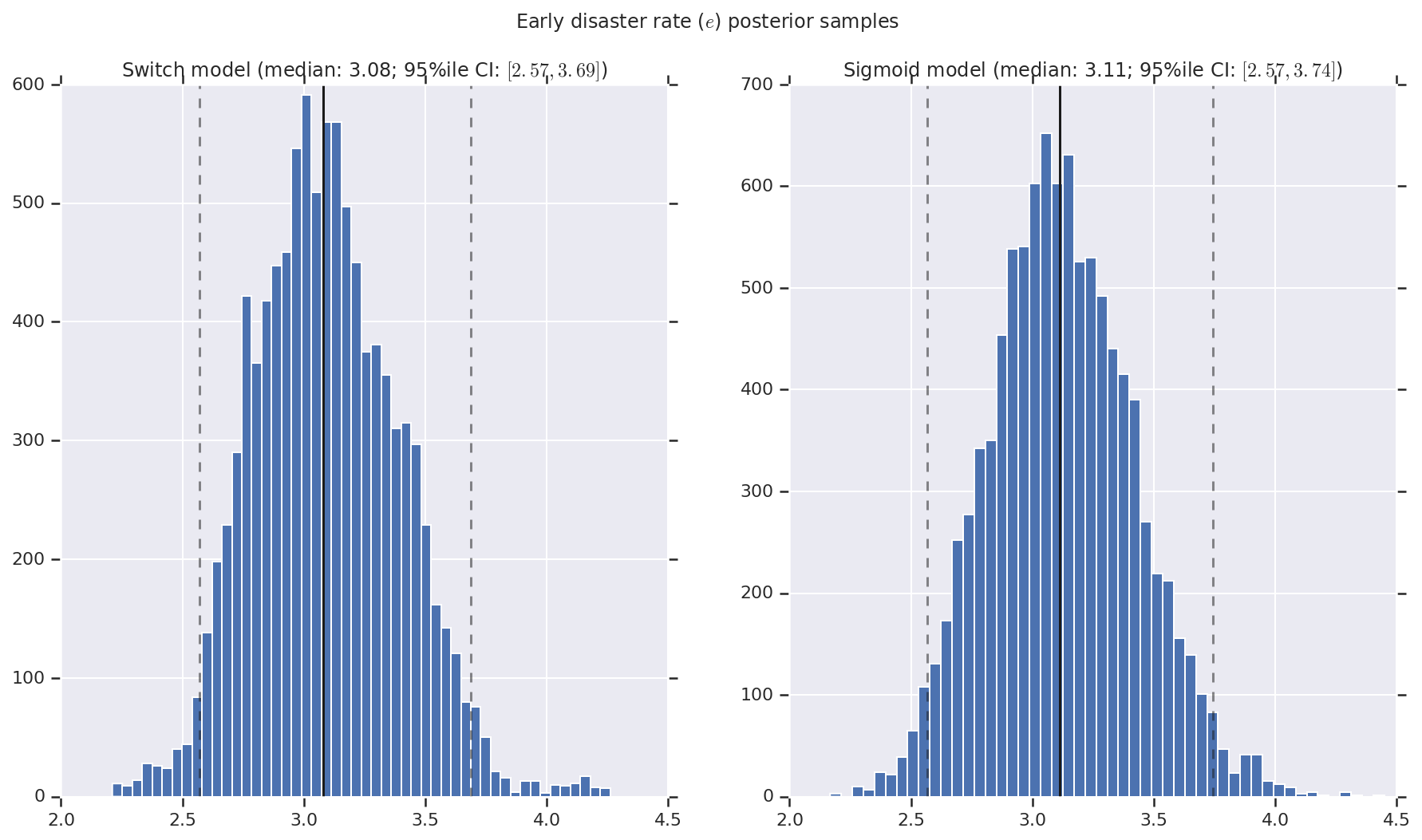
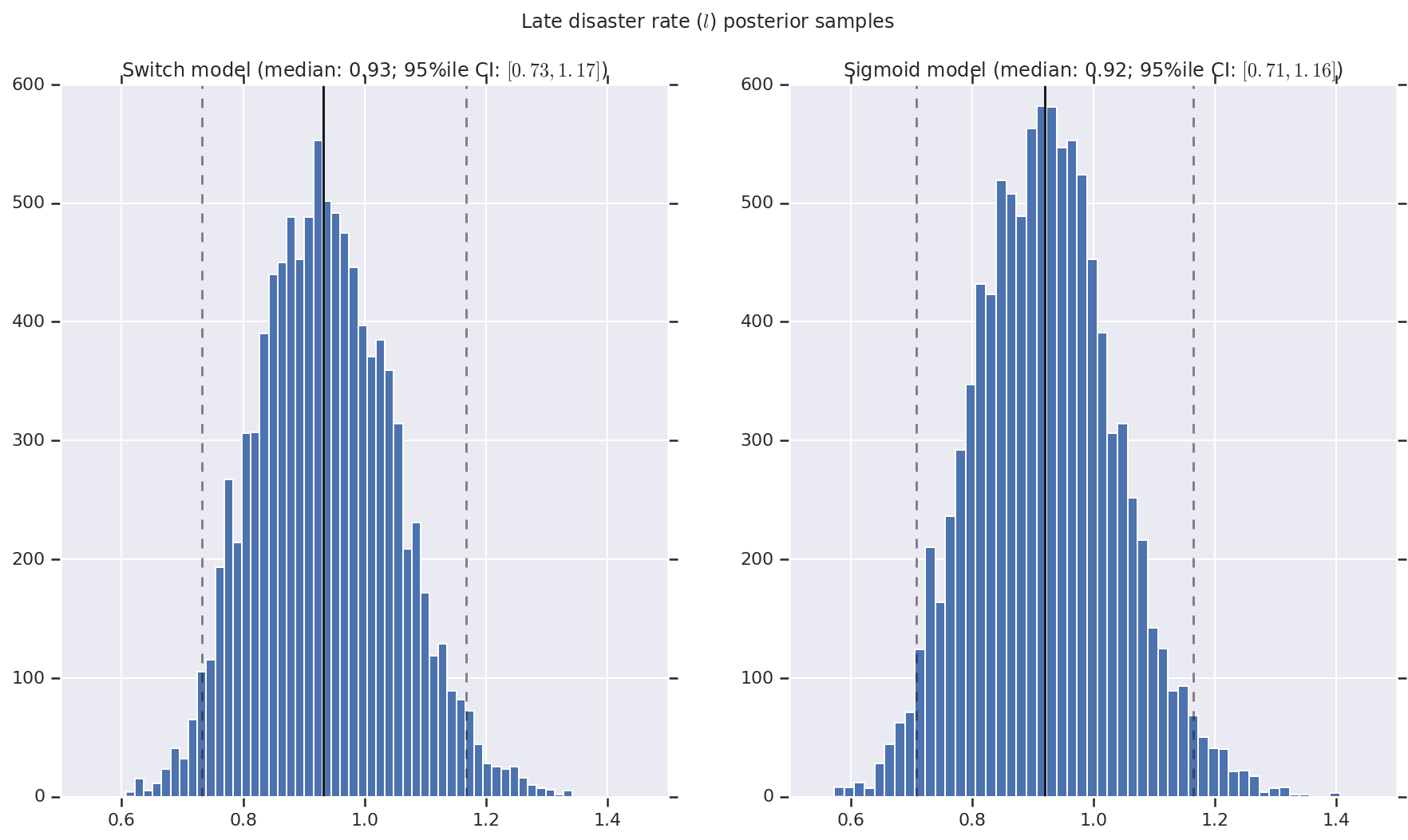
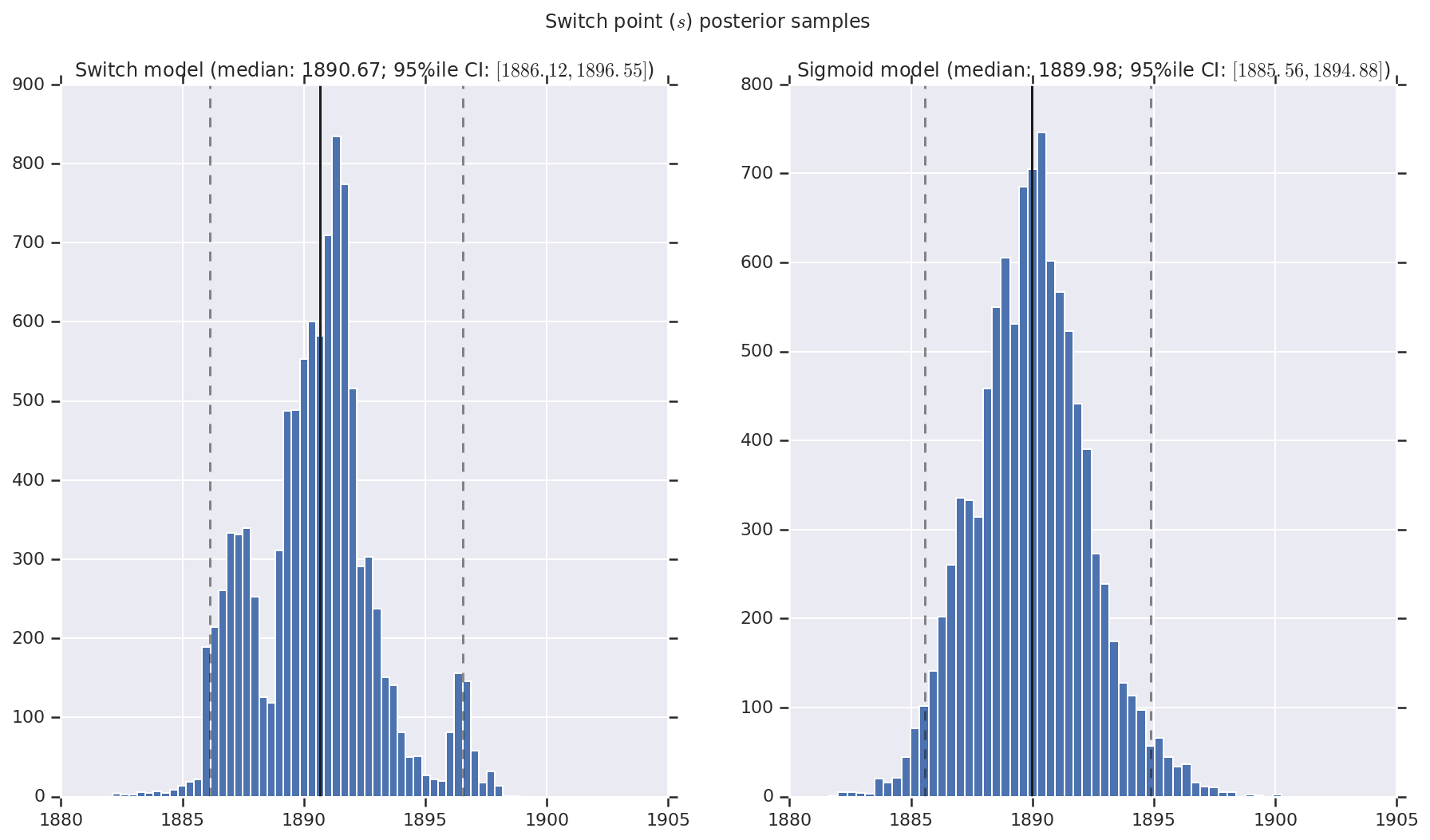
Visualizamos el resultado como histogramas de muestras de la distribución posterior para la tasa de desastre temprano y tardío, así como el punto de conmutación. Los histogramas se superponen con una línea sólida que representa la mediana de la muestra, así como los límites del intervalo creíble del 95% ile como líneas discontinuas.
def _desc(v):
return '(median: {}; 95%ile CI: $[{}, {}]$)'.format(
*np.round(np.percentile(v, [50, 2.5, 97.5]), 2))
for t, v in [
('Early disaster rate ($e$) posterior samples', early_disaster_rate),
('Late disaster rate ($l$) posterior samples', late_disaster_rate),
('Switch point ($s$) posterior samples', years[0] + switchpoint),
]:
fig, ax = plt.subplots(nrows=1, ncols=2, sharex=True)
for (m, i) in (('Switch', 0), ('Sigmoid', 1)):
a = ax[i]
a.hist(v[i], bins=50)
a.axvline(x=np.percentile(v[i], 50), color='k')
a.axvline(x=np.percentile(v[i], 2.5), color='k', ls='dashed', alpha=.5)
a.axvline(x=np.percentile(v[i], 97.5), color='k', ls='dashed', alpha=.5)
a.set_title(m + ' model ' + _desc(v[i]))
fig.suptitle(t)
plt.show()