TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
এই নোটবুক reimplements থেকে Bayesian "পরিবর্তন বিন্দু বিশ্লেষণ" উদাহরণ প্রসারিত pymc3 ডকুমেন্টেশন ।
পূর্বশর্ত
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (15,8)
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
ডেটাসেট
ডেটা সেটটি থেকে এখানে । নোট, সেখানে এই উদাহরণে আরেকটি সংস্করণ প্রায় ফ্লোটিং , কিন্তু এটা হয়েছে ডেটা "অনুপস্থিত" - যে ক্ষেত্রে আপনি অনুপস্থিত মানের আরোপ প্রয়োজন চাই। (অন্যথায় আপনার মডেল কখনই তার প্রাথমিক পরামিতিগুলি ছেড়ে যাবে না কারণ সম্ভাবনা ফাংশনটি অনির্ধারিত হবে।)
disaster_data = np.array([ 4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
2, 2, 3, 4, 2, 1, 3, 2, 2, 1, 1, 1, 1, 3, 0, 0,
1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
3, 3, 1, 1, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1])
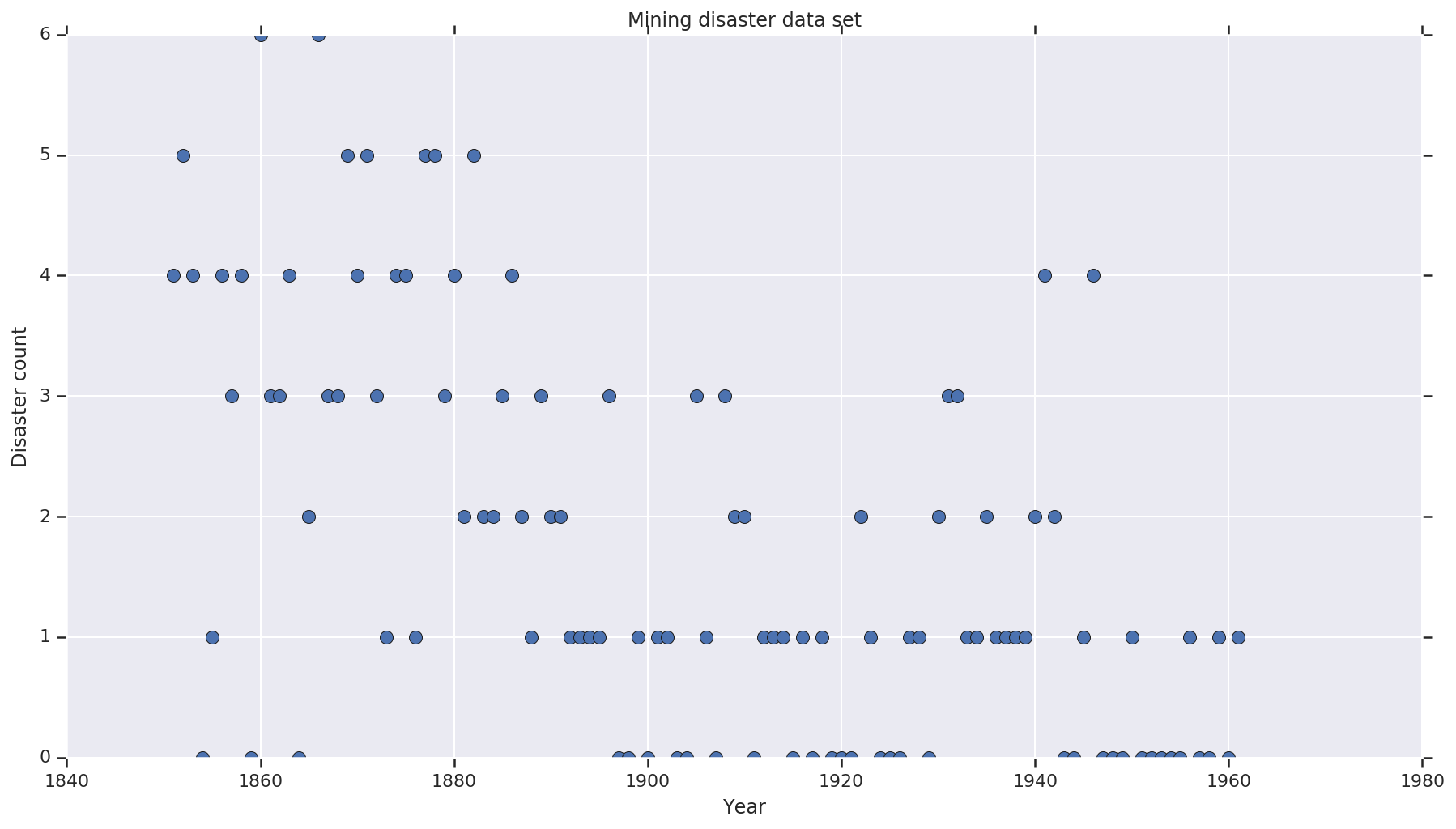
years = np.arange(1851, 1962)
plt.plot(years, disaster_data, 'o', markersize=8);
plt.ylabel('Disaster count')
plt.xlabel('Year')
plt.title('Mining disaster data set')
plt.show()
সম্ভাব্য মডেল
মডেলটি একটি "সুইচ পয়েন্ট" অনুমান করে (যেমন একটি বছর যে সময় নিরাপত্তা প্রবিধান পরিবর্তিত হয়েছে), এবং সেই সুইচ পয়েন্টের আগে এবং পরে ধ্রুবক (কিন্তু সম্ভাব্যভাবে ভিন্ন) হার সহ পয়সন-বিতরণ করা দুর্যোগের হার।
প্রকৃত দুর্যোগ গণনা স্থির (পর্যবেক্ষিত); এই মডেলের যেকোন নমুনাকে সুইচপয়েন্ট এবং দুর্যোগের "প্রাথমিক" এবং "দেরী" হার উভয়ই উল্লেখ করতে হবে।
মূল মডেল pymc3 ডকুমেন্টেশন উদাহরণ :
\[ \begin{align*} (D_t|s,e,l)&\sim \text{Poisson}(r_t), \\ & \,\quad\text{with}\; r_t = \begin{cases}e & \text{if}\; t < s\\l &\text{if}\; t \ge s\end{cases} \\ s&\sim\text{Discrete Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
যাইহোক, গড় দুর্যোগ হার \(r_t\) switchpoint এ বিচ্ছিন্নভাবে হয়েছে \(s\), যা তা না differentiable করে তোলে। সুতরাং এটা হ্যামিল্টনিয়ান মন্টে কার্লো (ক্ষেত্রে HMC) অ্যালগরিদম কোন গ্রেডিয়েন্ট সংকেত প্রদান করে - কিন্তু কারণ \(s\) পূর্বে একটানা, একটি র্যান্ডম হাঁটার ক্ষেত্রে HMC এর ফলব্যাক যথেষ্ট এই উদাহরণে উচ্চ সম্ভাবনা ভর এলাকায় খুঁজতে হয়।
একটি দ্বিতীয় মডেল হিসেবে, আমরা একটি ব্যবহার করে প্রকৃত মডেল পরিবর্তন সিগমা "সুইচ" e এবং ঠ মধ্যে রূপান্তরটি differentiable করতে, এবং switchpoint জন্য ক্রমাগত অভিন্ন বন্টন ব্যবহার করতে হবে \(s\)। (কেউ যুক্তি দিতে পারে যে এই মডেলটি বাস্তবে আরও সত্য, কারণ একটি "সুইচ" গড় হারে সম্ভবত একাধিক বছর ধরে প্রসারিত হবে।) নতুন মডেলটি এইভাবে:
\[ \begin{align*} (D_t|s,e,l)&\sim\text{Poisson}(r_t), \\ & \,\quad \text{with}\; r_t = e + \frac{1}{1+\exp(s-t)}(l-e) \\ s&\sim\text{Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
আরও তথ্যের অভাবে আমরা অনুমান \(r_e = r_l = 1\) গতকাল দেশের সর্বোচ্চ তাপমাত্রা জন্য পরামিতি হিসেবে। আমরা উভয় মডেল চালাব এবং তাদের অনুমান ফলাফল তুলনা করব।
def disaster_count_model(disaster_rate_fn):
disaster_count = tfd.JointDistributionNamed(dict(
e=tfd.Exponential(rate=1.),
l=tfd.Exponential(rate=1.),
s=tfd.Uniform(0., high=len(years)),
d_t=lambda s, l, e: tfd.Independent(
tfd.Poisson(rate=disaster_rate_fn(np.arange(len(years)), s, l, e)),
reinterpreted_batch_ndims=1)
))
return disaster_count
def disaster_rate_switch(ys, s, l, e):
return tf.where(ys < s, e, l)
def disaster_rate_sigmoid(ys, s, l, e):
return e + tf.sigmoid(ys - s) * (l - e)
model_switch = disaster_count_model(disaster_rate_switch)
model_sigmoid = disaster_count_model(disaster_rate_sigmoid)
উপরের কোডটি জয়েন্ট ডিস্ট্রিবিউশন সিকোয়েন্সিয়াল ডিস্ট্রিবিউশনের মাধ্যমে মডেলটিকে সংজ্ঞায়িত করে। disaster_rate ফাংশন একটি অ্যারের সাথে বলা হয় [0, ..., len(years)-1] একটি ভেক্টর উত্পাদন করতে len(years) র্যান্ডম ভেরিয়েবল - সামনে বছর switchpoint হয় early_disaster_rate পর বেশী late_disaster_rate (modulo সিগমায়েড রূপান্তর)।
টার্গেট লগ প্রোব ফাংশনটি বুদ্ধিমান কিনা তা এখানে একটি বিবেক-চেক করা হয়েছে:
def target_log_prob_fn(model, s, e, l):
return model.log_prob(s=s, e=e, l=l, d_t=disaster_data)
models = [model_switch, model_sigmoid]
print([target_log_prob_fn(m, 40., 3., .9).numpy() for m in models]) # Somewhat likely result
print([target_log_prob_fn(m, 60., 1., 5.).numpy() for m in models]) # Rather unlikely result
print([target_log_prob_fn(m, -10., 1., 1.).numpy() for m in models]) # Impossible result
[-176.94559, -176.28717] [-371.3125, -366.8816] [-inf, -inf]
HMC Bayesian অনুমান করতে
আমরা প্রয়োজনীয় ফলাফল এবং বার্ন-ইন পদক্ষেপের সংখ্যা নির্ধারণ করি; কোড বেশিরভাগই অনুকরণে করা হয় tfp.mcmc.HamiltonianMonteCarlo ডকুমেন্টেশন । এটি একটি অভিযোজিত পদক্ষেপের আকার ব্যবহার করে (অন্যথায় ফলাফলটি নির্বাচিত পদক্ষেপের আকারের মানটির প্রতি খুব সংবেদনশীল)। আমরা শৃঙ্খলের প্রাথমিক অবস্থা হিসাবে একের মান ব্যবহার করি।
যদিও এটি সম্পূর্ণ গল্প নয়। আপনি যদি উপরের মডেলের সংজ্ঞায় ফিরে যান, আপনি লক্ষ্য করবেন যে কিছু সম্ভাব্যতা বন্টন সম্পূর্ণ বাস্তব সংখ্যা লাইনে সু-সংজ্ঞায়িত নয়। অতএব আমরা স্থান যে ক্ষেত্রে HMC একটি সঙ্গে ক্ষেত্রে HMC কার্নেল মোড়কে পরীক্ষা হইবে সীমাবদ্ধ TransformedTransitionKernel যে নির্দিষ্ট করে এগিয়ে bijectors ডোমেন সম্ভাব্যতা বিতরণের উপর সংজ্ঞায়িত করা হয় (নীচের কোডে মন্তব্য দেখুন) সম্মুখের বাস্তব সংখ্যার রুপান্তর।
num_results = 10000
num_burnin_steps = 3000
@tf.function(autograph=False, jit_compile=True)
def make_chain(target_log_prob_fn):
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.05,
num_leapfrog_steps=3),
bijector=[
# The switchpoint is constrained between zero and len(years).
# Hence we supply a bijector that maps the real numbers (in a
# differentiable way) to the interval (0;len(yers))
tfb.Sigmoid(low=0., high=tf.cast(len(years), dtype=tf.float32)),
# Early and late disaster rate: The exponential distribution is
# defined on the positive real numbers
tfb.Softplus(),
tfb.Softplus(),
])
kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=int(0.8*num_burnin_steps))
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
# The three latent variables
tf.ones([], name='init_switchpoint'),
tf.ones([], name='init_early_disaster_rate'),
tf.ones([], name='init_late_disaster_rate'),
],
trace_fn=None,
kernel=kernel)
return states
switch_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_switch, *args))]
sigmoid_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_sigmoid, *args))]
switchpoint, early_disaster_rate, late_disaster_rate = zip(
switch_samples, sigmoid_samples)
উভয় মডেল সমান্তরালভাবে চালান:
ফলাফলটি কল্পনা করুন
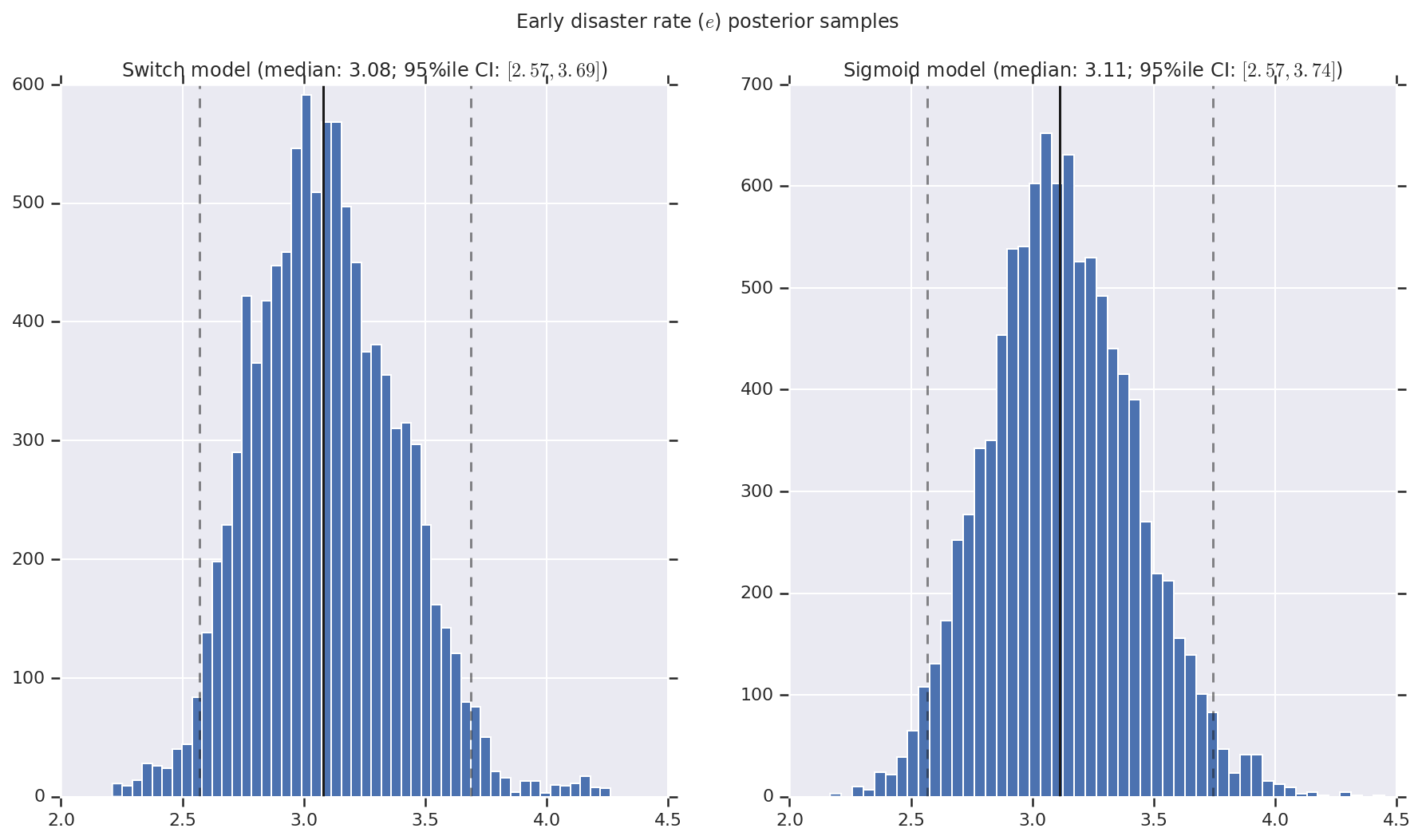
আমরা ফলাফলটিকে প্রারম্ভিক এবং দেরী বিপর্যয়ের হার, সেইসাথে স্যুইচপয়েন্টের জন্য পশ্চাদবর্তী বিতরণের নমুনার হিস্টোগ্রাম হিসাবে কল্পনা করি। হিস্টোগ্রামগুলি নমুনা মধ্যকার প্রতিনিধিত্বকারী একটি কঠিন রেখা দিয়ে ওভারলেড করা হয়, সেইসাথে ড্যাশড লাইন হিসাবে 95% ile বিশ্বাসযোগ্য ব্যবধানের সীমানা।
def _desc(v):
return '(median: {}; 95%ile CI: $[{}, {}]$)'.format(
*np.round(np.percentile(v, [50, 2.5, 97.5]), 2))
for t, v in [
('Early disaster rate ($e$) posterior samples', early_disaster_rate),
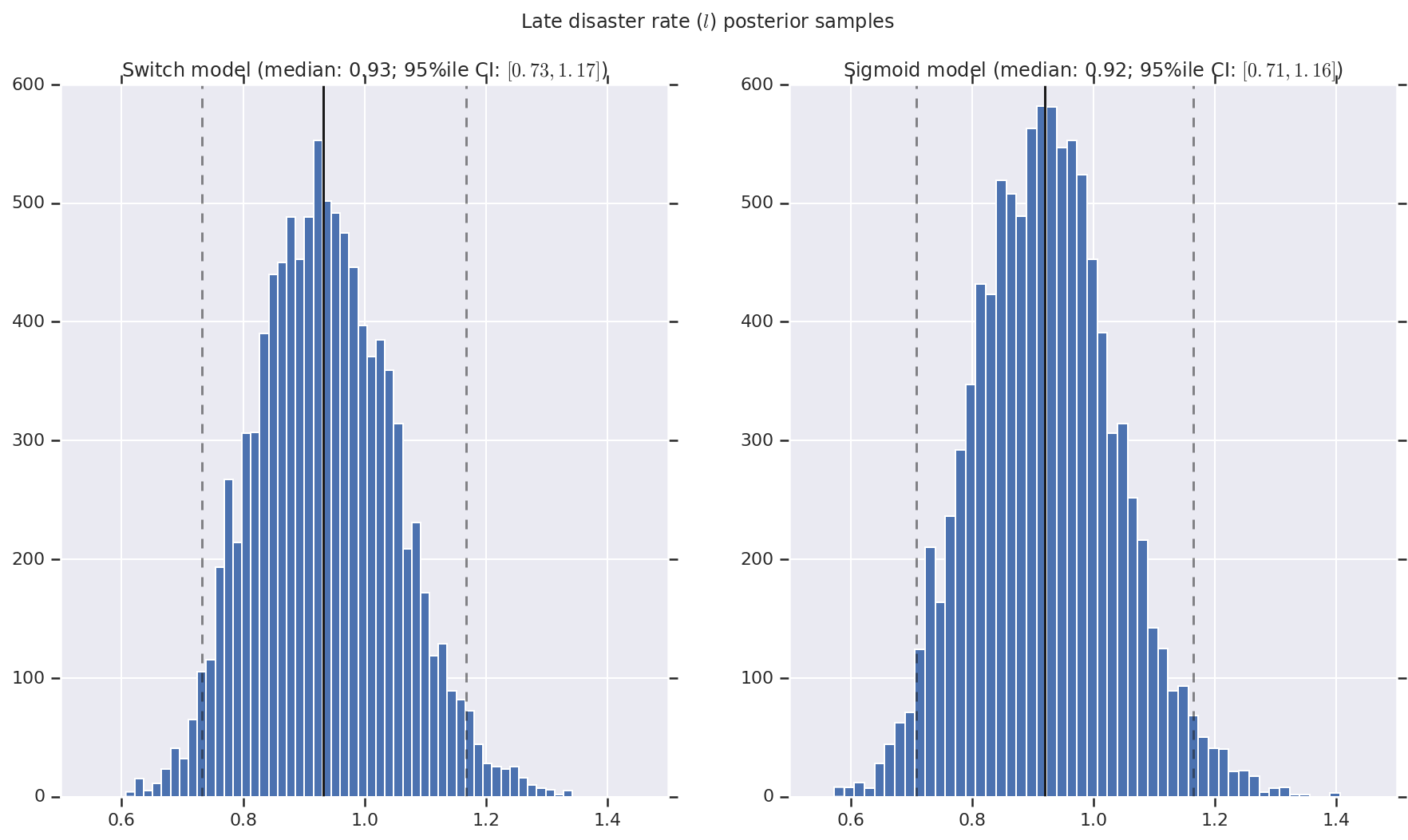
('Late disaster rate ($l$) posterior samples', late_disaster_rate),
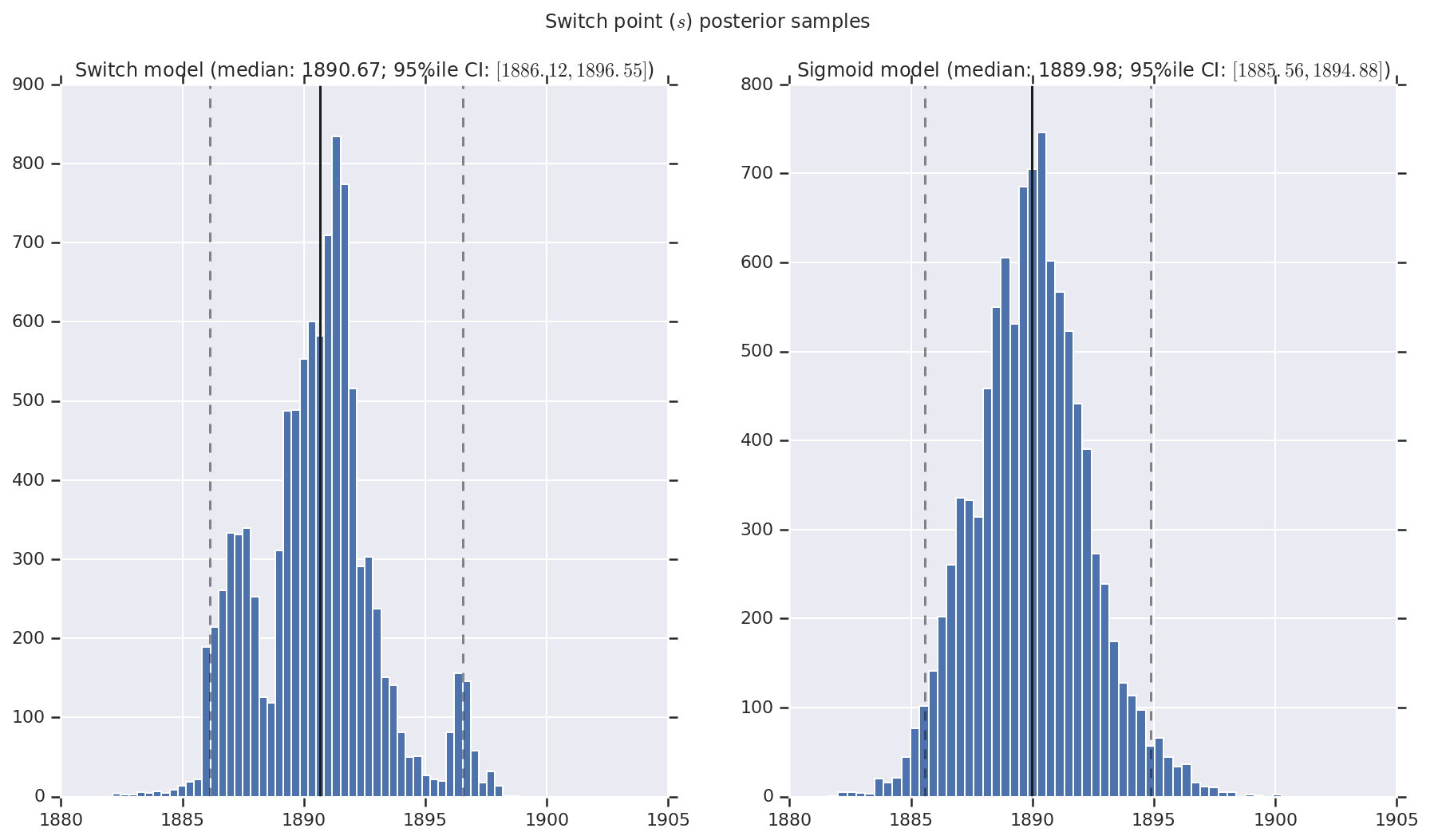
('Switch point ($s$) posterior samples', years[0] + switchpoint),
]:
fig, ax = plt.subplots(nrows=1, ncols=2, sharex=True)
for (m, i) in (('Switch', 0), ('Sigmoid', 1)):
a = ax[i]
a.hist(v[i], bins=50)
a.axvline(x=np.percentile(v[i], 50), color='k')
a.axvline(x=np.percentile(v[i], 2.5), color='k', ls='dashed', alpha=.5)
a.axvline(x=np.percentile(v[i], 97.5), color='k', ls='dashed', alpha=.5)
a.set_title(m + ' model ' + _desc(v[i]))
fig.suptitle(t)
plt.show()