 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Bu ortak çalışmada, yalnızca TensorFlow Olasılık temel öğelerini kullanarak bir Bayes Gauss Karışım Modeli'nin (BGMM) arkasından örneklemeyi keşfedeceğiz.
modeli
İçin \(k\in\{1,\ldots, K\}\) boyutu her karışım bileşenleri \(D\), model istiyorum \(i\in\{1,\ldots,N\}\) Aşağıdaki Bayes Gauss Karışım Modeli kullanılarak örnekleri Ild:
\[\begin{align*} \theta &\sim \text{Dirichlet}(\text{concentration}=\alpha_0)\\ \mu_k &\sim \text{Normal}(\text{loc}=\mu_{0k}, \text{scale}=I_D)\\ T_k &\sim \text{Wishart}(\text{df}=5, \text{scale}=I_D)\\ Z_i &\sim \text{Categorical}(\text{probs}=\theta)\\ Y_i &\sim \text{Normal}(\text{loc}=\mu_{z_i}, \text{scale}=T_{z_i}^{-1/2})\\ \end{align*}\]
Not scale argümanlar tümüne sahip cholesky anlambilim. Bu kuralı kullanıyoruz çünkü TF Distributions'ınki (bu kuralın kendisi de kısmen hesaplama açısından avantajlı olduğu için kullanıyor).
Amacımız posteriordan örnekler oluşturmaktır:
\[p\left(\theta, \{\mu_k, T_k\}_{k=1}^K \Big| \{y_i\}_{i=1}^N, \alpha_0, \{\mu_{ok}\}_{k=1}^K\right)\]
O Bildirimi \(\{Z_i\}_{i=1}^N\) mevcut değil - ile ölçekli değil sadece bu rastgele değişkenlerin ilgilenen döndük \(N\). (Ve neyse ki dışarı marjinalleştirmekten işleyen bir TF dağılımı var \(Z_i\).)
Hesaplamalı olarak zorlu bir normalizasyon terimi nedeniyle bu dağılımdan doğrudan örnek almak mümkün değildir.
Metropolis- Hastings algoritmaları dirençli-to-normale dağılımlardan örneği almak için bir tekniktir.
TensorFlow Probability, Metropolis-Hastings'e dayalı birkaçı da dahil olmak üzere bir dizi MCMC seçeneği sunar. Bu defterin, biz kullanacağız Hamilton Monte Carlo ( tfp.mcmc.HamiltonianMonteCarlo ). HMC genellikle iyi bir seçimdir çünkü hızla yakınsayabilir, durum uzayını ortaklaşa örnekleyebilir (koordinatlı olarak değil) ve TF'nin erdemlerinden birini kullanır: otomatik farklılaşma. Aslında daha iyi mesela diğer yaklaşımlar, tarafından yapılabilir olabilecek bir BGMM posterior örnekleme dedi Gibb en örnekleme .
%matplotlib inline
import functools
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import seaborn as sns; sns.set_context('notebook')
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
physical_devices = tf.config.experimental.list_physical_devices('GPU')
if len(physical_devices) > 0:
tf.config.experimental.set_memory_growth(physical_devices[0], True)
Modeli gerçekten oluşturmadan önce, yeni bir dağıtım türü tanımlamamız gerekecek. Yukarıdaki model spesifikasyonundan, MVN'yi bir ters kovaryans matrisiyle, yani [hassasiyet matrisi](https://en.wikipedia.org/wiki/Precision_(statistics%29) ile parametreleştirdiğimiz açıktır. TF, bizim dışarı rulo gerekir Bijector Bu. Bijector ileri dönüşümü kullanacağız:
-
Y = tf.linalg.triangular_solve((tf.linalg.matrix_transpose(chol_precision_tril), X, adjoint=True) + loc.
Ve log_prob hesaplama sadece ters, yani geçerli:
-
X = tf.linalg.matmul(chol_precision_tril, X - loc, adjoint_a=True).
HMC için hepimiz ihtiyacı olduğundan log_prob , bu araçlar biz çağıran hiç önlemek tf.linalg.triangular_solve (için geçerli olacağı gibi tfd.MultivariateNormalTriL ). Bu yana avantajlıdır tf.linalg.matmul genellikle daha hızlı daha iyi önbellek mevkiinde sayesindedir.
class MVNCholPrecisionTriL(tfd.TransformedDistribution):
"""MVN from loc and (Cholesky) precision matrix."""
def __init__(self, loc, chol_precision_tril, name=None):
super(MVNCholPrecisionTriL, self).__init__(
distribution=tfd.Independent(tfd.Normal(tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=chol_precision_tril,
adjoint=True)),
]),
name=name)
tfd.Independent dağıtım dönüşler bağımsız istatistiksel bağımsız koordinatlarla çok değişkenli dağılım içine, bir dağılımın çizer. İşlem açısından log_prob , olay boyut (lar) üzerinde basit bir toplamı olarak bu "meta dağılımı" tezahür.
Ayrıca aldığını fark adjoint ölçekli matris ( "devrik"). Bunun nedeni hassas ters kovaryans, yani eğer \(P=C^{-1}\) ve eğer \(C=AA^\top\)ardından \(P=BB^{\top}\) \(B=A^{-\top}\).
Bu dağılım tür zor ait olduğundan, en hızlı şekilde doğrulamak izin MVNCholPrecisionTriL biz gerektiğini düşünüyorum gibi çalışır.
def compute_sample_stats(d, seed=42, n=int(1e6)):
x = d.sample(n, seed=seed)
sample_mean = tf.reduce_mean(x, axis=0, keepdims=True)
s = x - sample_mean
sample_cov = tf.linalg.matmul(s, s, adjoint_a=True) / tf.cast(n, s.dtype)
sample_scale = tf.linalg.cholesky(sample_cov)
sample_mean = sample_mean[0]
return [
sample_mean,
sample_cov,
sample_scale,
]
dtype = np.float32
true_loc = np.array([1., -1.], dtype=dtype)
true_chol_precision = np.array([[1., 0.],
[2., 8.]],
dtype=dtype)
true_precision = np.matmul(true_chol_precision, true_chol_precision.T)
true_cov = np.linalg.inv(true_precision)
d = MVNCholPrecisionTriL(
loc=true_loc,
chol_precision_tril=true_chol_precision)
[sample_mean, sample_cov, sample_scale] = [
t.numpy() for t in compute_sample_stats(d)]
print('true mean:', true_loc)
print('sample mean:', sample_mean)
print('true cov:\n', true_cov)
print('sample cov:\n', sample_cov)
true mean: [ 1. -1.] sample mean: [ 1.0002806 -1.000105 ] true cov: [[ 1.0625 -0.03125 ] [-0.03125 0.015625]] sample cov: [[ 1.0641273 -0.03126175] [-0.03126175 0.01559312]]
Örnek ortalama ve kovaryans, gerçek ortalamaya ve kovaryansa yakın olduğundan, dağılımın doğru bir şekilde uygulandığı görülüyor. Şimdi, biz kullanacağız MVNCholPrecisionTriL tfp.distributions.JointDistributionNamed BGMM modelini belirlemek için. Gözlemsel modeli için, kullanacağız tfd.MixtureSameFamily otomatik entegre etmek \(\{Z_i\}_{i=1}^N\) çizer.
dtype = np.float64
dims = 2
components = 3
num_samples = 1000
bgmm = tfd.JointDistributionNamed(dict(
mix_probs=tfd.Dirichlet(
concentration=np.ones(components, dtype) / 10.),
loc=tfd.Independent(
tfd.Normal(
loc=np.stack([
-np.ones(dims, dtype),
np.zeros(dims, dtype),
np.ones(dims, dtype),
]),
scale=tf.ones([components, dims], dtype)),
reinterpreted_batch_ndims=2),
precision=tfd.Independent(
tfd.WishartTriL(
df=5,
scale_tril=np.stack([np.eye(dims, dtype=dtype)]*components),
input_output_cholesky=True),
reinterpreted_batch_ndims=1),
s=lambda mix_probs, loc, precision: tfd.Sample(tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(probs=mix_probs),
components_distribution=MVNCholPrecisionTriL(
loc=loc,
chol_precision_tril=precision)),
sample_shape=num_samples)
))
def joint_log_prob(observations, mix_probs, loc, chol_precision):
"""BGMM with priors: loc=Normal, precision=Inverse-Wishart, mix=Dirichlet.
Args:
observations: `[n, d]`-shaped `Tensor` representing Bayesian Gaussian
Mixture model draws. Each sample is a length-`d` vector.
mix_probs: `[K]`-shaped `Tensor` representing random draw from
`Dirichlet` prior.
loc: `[K, d]`-shaped `Tensor` representing the location parameter of the
`K` components.
chol_precision: `[K, d, d]`-shaped `Tensor` representing `K` lower
triangular `cholesky(Precision)` matrices, each being sampled from
a Wishart distribution.
Returns:
log_prob: `Tensor` representing joint log-density over all inputs.
"""
return bgmm.log_prob(
mix_probs=mix_probs, loc=loc, precision=chol_precision, s=observations)
"Eğitim" Verileri Oluşturun
Bu demo için bazı rastgele verileri örnekleyeceğiz.
true_loc = np.array([[-2., -2],
[0, 0],
[2, 2]], dtype)
random = np.random.RandomState(seed=43)
true_hidden_component = random.randint(0, components, num_samples)
observations = (true_loc[true_hidden_component] +
random.randn(num_samples, dims).astype(dtype))
HMC kullanarak Bayes Çıkarımı
Artık modelimizi belirtmek için TFD'yi kullandığımıza ve bazı gözlemlenen verileri elde ettiğimize göre, HMC'yi çalıştırmak için gerekli tüm parçalara sahibiz.
Bunu yapmak için, bir kullanacağız kısmi uygulama örneklemde istemiyoruz şeyler "aşağı pin" için. Bu durumda araçlar sadece aşağı pin gerek olduğunu observations . (Hiper parametreler zaten önceden dağılımları ve olmayan kısmına pişirilmektedir joint_log_prob fonksiyon imza.)
unnormalized_posterior_log_prob = functools.partial(joint_log_prob, observations)
initial_state = [
tf.fill([components],
value=np.array(1. / components, dtype),
name='mix_probs'),
tf.constant(np.array([[-2., -2],
[0, 0],
[2, 2]], dtype),
name='loc'),
tf.linalg.eye(dims, batch_shape=[components], dtype=dtype, name='chol_precision'),
]
Sınırsız Temsil
Hamiltonian Monte Carlo (HMC), hedef log-olasılık fonksiyonunun argümanlarına göre türevlenebilir olmasını gerektirir. Ayrıca, durum uzayı kısıtlanmamışsa, HMC önemli ölçüde daha yüksek istatistiksel verimlilik sergileyebilir.
Bu, BGMM posteriorundan örnekleme yaparken iki ana sorunu çözmemiz gerektiği anlamına gelir:
- \(\theta\) yani ayrı bir olasılık vektörünü temsil eder, gibi olmalıdır \(\sum_{k=1}^K \theta_k = 1\) ve \(\theta_k>0\).
- \(T_k\) temsil eden bir ters kovaryans matrisi, yani, o şekilde olması gerekir \(T_k \succ 0\)yani, bir pozitif tanımlı .
Bu gereksinimi gidermek için şunları yapmamız gerekir:
- kısıtlı değişkenleri kısıtsız bir alana dönüştürün
- MCMC'yi sınırsız alanda çalıştırın
- kısıtlanmamış değişkenleri kısıtlı alana geri dönüştürün.
Olduğu gibi MVNCholPrecisionTriL , biz kullanacağız Bijector ler kısıtsız boşluğa rastgele değişkenler dönüştürmek için.
Dirichletile serbest boşluğa dönüştürülmüştür SoftMax fonksiyonu .Hassas rastgele değişkenimiz, pozitif yarı tanımlı matrisler üzerindeki bir dağılımdır. Bu serbest bırak için kullanacağımız
FillTriangularveTransformDiagonalbijectors. Bunlar vektörleri alt üçgen matrislere dönüştürür ve köşegenin pozitif olmasını sağlar. Sadece örnekleme sağlayan, çünkü eski yararlıdır \(d(d+1)/2\) yerine yüzen \(d^2\).
unconstraining_bijectors = [
tfb.SoftmaxCentered(),
tfb.Identity(),
tfb.Chain([
tfb.TransformDiagonal(tfb.Softplus()),
tfb.FillTriangular(),
])]
@tf.function(autograph=False)
def sample():
return tfp.mcmc.sample_chain(
num_results=2000,
num_burnin_steps=500,
current_state=initial_state,
kernel=tfp.mcmc.SimpleStepSizeAdaptation(
tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior_log_prob,
step_size=0.065,
num_leapfrog_steps=5),
bijector=unconstraining_bijectors),
num_adaptation_steps=400),
trace_fn=lambda _, pkr: pkr.inner_results.inner_results.is_accepted)
[mix_probs, loc, chol_precision], is_accepted = sample()
Şimdi zinciri uygulayacağız ve arka araçları yazdıracağız.
acceptance_rate = tf.reduce_mean(tf.cast(is_accepted, dtype=tf.float32)).numpy()
mean_mix_probs = tf.reduce_mean(mix_probs, axis=0).numpy()
mean_loc = tf.reduce_mean(loc, axis=0).numpy()
mean_chol_precision = tf.reduce_mean(chol_precision, axis=0).numpy()
precision = tf.linalg.matmul(chol_precision, chol_precision, transpose_b=True)
print('acceptance_rate:', acceptance_rate)
print('avg mix probs:', mean_mix_probs)
print('avg loc:\n', mean_loc)
print('avg chol(precision):\n', mean_chol_precision)
acceptance_rate: 0.5305 avg mix probs: [0.25248723 0.60729516 0.1402176 ] avg loc: [[-1.96466753 -2.12047249] [ 0.27628865 0.22944732] [ 2.06461244 2.54216122]] avg chol(precision): [[[ 1.05105032 0. ] [ 0.12699955 1.06553113]] [[ 0.76058015 0. ] [-0.50332767 0.77947431]] [[ 1.22770457 0. ] [ 0.70670027 1.50914164]]]
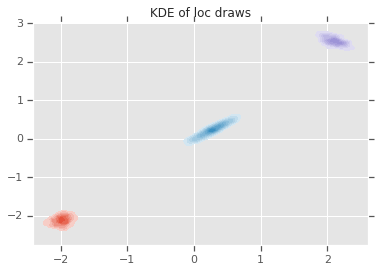
loc_ = loc.numpy()
ax = sns.kdeplot(loc_[:,0,0], loc_[:,0,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,1,0], loc_[:,1,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,2,0], loc_[:,2,1], shade=True, shade_lowest=False)
plt.title('KDE of loc draws');
Çözüm
Bu basit ortak çalışma, hiyerarşik Bayes karışım modelleri oluşturmak için TensorFlow Olasılık ilkellerinin nasıl kullanılabileceğini gösterdi.
