 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
W ramach tej współpracy przyjrzymy się próbkowaniu od tyłu Bayesian Gaussian Mixture Model (BGMM) przy użyciu tylko prymitywów TensorFlow Probability.
Model
Dla \(k\in\{1,\ldots, K\}\) składników mieszaniny każdego z wymiarów \(D\), chcielibyśmy modelu \(i\in\{1,\ldots,N\}\) IID próbki stosując następujące Bayesa Gaussa modelowej mieszaniny:
\[\begin{align*} \theta &\sim \text{Dirichlet}(\text{concentration}=\alpha_0)\\ \mu_k &\sim \text{Normal}(\text{loc}=\mu_{0k}, \text{scale}=I_D)\\ T_k &\sim \text{Wishart}(\text{df}=5, \text{scale}=I_D)\\ Z_i &\sim \text{Categorical}(\text{probs}=\theta)\\ Y_i &\sim \text{Normal}(\text{loc}=\mu_{z_i}, \text{scale}=T_{z_i}^{-1/2})\\ \end{align*}\]
Zauważ, że scale argumenty mają cholesky semantykę. Używamy tej konwencji, ponieważ jest to konwencja dystrybucji TF (która sama korzysta z tej konwencji po części, ponieważ jest ona korzystna obliczeniowo).
Naszym celem jest wygenerowanie próbek z tyłu:
\[p\left(\theta, \{\mu_k, T_k\}_{k=1}^K \Big| \{y_i\}_{i=1}^N, \alpha_0, \{\mu_{ok}\}_{k=1}^K\right)\]
Zauważ, że \(\{Z_i\}_{i=1}^N\) nie jest obecny - dokładamy zainteresowany tylko tych zmiennych losowych, które nie skalują się z \(N\). (I na szczęście istnieje dystrybucja TF który obsługuje marginalizacji się \(Z_i\)).
Nie jest możliwe bezpośrednie próbkowanie z tego rozkładu ze względu na niewykonalny obliczeniowo termin normalizacji.
Algorytmy Metropolisa Hastings to technika do pobierania próbek z rozkładu trudnych do być normą.
TensorFlow Probability oferuje szereg opcji MCMC, w tym kilka opartych na Metropolis-Hastings. W tym notebooku, użyjemy Hamiltona Monte Carlo ( tfp.mcmc.HamiltonianMonteCarlo ). HMC jest często dobrym wyborem, ponieważ może szybko się zbiegać, próbkować wspólnie przestrzeń stanów (w przeciwieństwie do współrzędności) i wykorzystuje jedną z zalet TF: automatyczne różnicowanie. Powiedział, że pobieranie próbek z tylnej BGMM faktycznie może być lepiej zrobione przez innych metod, np próbkowania Gibb za .
%matplotlib inline
import functools
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import seaborn as sns; sns.set_context('notebook')
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
physical_devices = tf.config.experimental.list_physical_devices('GPU')
if len(physical_devices) > 0:
tf.config.experimental.set_memory_growth(physical_devices[0], True)
Zanim zaczniemy budować model, musimy zdefiniować nowy typ dystrybucji. Z powyższej specyfikacji modelu jasno wynika, że parametryzujemy MVN za pomocą odwrotnej macierzy kowariancji, tj. [macierz precyzji](https://en.wikipedia.org/wiki/Precision_(statistics%29). Aby to osiągnąć w TF, musimy toczyć naszą Bijector to. Bijector użyje transformację do przodu:
-
Y = tf.linalg.triangular_solve((tf.linalg.matrix_transpose(chol_precision_tril), X, adjoint=True) + loc.
A log_prob kalkulacja jest tylko odwrotną, tj:
-
X = tf.linalg.matmul(chol_precision_tril, X - loc, adjoint_a=True).
Ponieważ wszystko, co potrzeba HMC jest log_prob oznacza to unikamy kiedykolwiek nazywając tf.linalg.triangular_solve (jak byłoby w przypadku tfd.MultivariateNormalTriL ). Jest to korzystne, ponieważ tf.linalg.matmul jest zwykle szybciej dzięki lepszej cache miejscowości.
class MVNCholPrecisionTriL(tfd.TransformedDistribution):
"""MVN from loc and (Cholesky) precision matrix."""
def __init__(self, loc, chol_precision_tril, name=None):
super(MVNCholPrecisionTriL, self).__init__(
distribution=tfd.Independent(tfd.Normal(tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=chol_precision_tril,
adjoint=True)),
]),
name=name)
tfd.Independent niezależne obroty dystrybucja czerpie z jednej dystrybucji, w wieloczynnikowej dystrybucji ze statystycznie niezależnych współrzędnych. W zakresie informatyki log_prob , to „meta-dystrybucją” manifestuje się jako prostą sumę ponad wymiaru zdarzenie (zdarzenia).
Zauważ też, że wzięliśmy adjoint ( „transpozycji”) z matrycą skalę. To dlatego, że jeśli dokładność jest odwrotnością kowariancji, czyli \(P=C^{-1}\) a jeśli \(C=AA^\top\), następnie \(P=BB^{\top}\) gdzie \(B=A^{-\top}\).
Ponieważ ta dystrybucja jest trochę trudne, niech szybko sprawdzić, czy nasz MVNCholPrecisionTriL działa jak uważamy, że powinno.
def compute_sample_stats(d, seed=42, n=int(1e6)):
x = d.sample(n, seed=seed)
sample_mean = tf.reduce_mean(x, axis=0, keepdims=True)
s = x - sample_mean
sample_cov = tf.linalg.matmul(s, s, adjoint_a=True) / tf.cast(n, s.dtype)
sample_scale = tf.linalg.cholesky(sample_cov)
sample_mean = sample_mean[0]
return [
sample_mean,
sample_cov,
sample_scale,
]
dtype = np.float32
true_loc = np.array([1., -1.], dtype=dtype)
true_chol_precision = np.array([[1., 0.],
[2., 8.]],
dtype=dtype)
true_precision = np.matmul(true_chol_precision, true_chol_precision.T)
true_cov = np.linalg.inv(true_precision)
d = MVNCholPrecisionTriL(
loc=true_loc,
chol_precision_tril=true_chol_precision)
[sample_mean, sample_cov, sample_scale] = [
t.numpy() for t in compute_sample_stats(d)]
print('true mean:', true_loc)
print('sample mean:', sample_mean)
print('true cov:\n', true_cov)
print('sample cov:\n', sample_cov)
true mean: [ 1. -1.] sample mean: [ 1.0002806 -1.000105 ] true cov: [[ 1.0625 -0.03125 ] [-0.03125 0.015625]] sample cov: [[ 1.0641273 -0.03126175] [-0.03126175 0.01559312]]
Ponieważ średnia próbki i kowariancja są zbliżone do prawdziwej średniej i kowariancji, wydaje się, że rozkład został prawidłowo zaimplementowany. Teraz użyjemy MVNCholPrecisionTriL tfp.distributions.JointDistributionNamed określić model BGMM. Do obserwacji modelu, użyjemy tfd.MixtureSameFamily automatycznie zintegrować się z \(\{Z_i\}_{i=1}^N\) rysuje.
dtype = np.float64
dims = 2
components = 3
num_samples = 1000
bgmm = tfd.JointDistributionNamed(dict(
mix_probs=tfd.Dirichlet(
concentration=np.ones(components, dtype) / 10.),
loc=tfd.Independent(
tfd.Normal(
loc=np.stack([
-np.ones(dims, dtype),
np.zeros(dims, dtype),
np.ones(dims, dtype),
]),
scale=tf.ones([components, dims], dtype)),
reinterpreted_batch_ndims=2),
precision=tfd.Independent(
tfd.WishartTriL(
df=5,
scale_tril=np.stack([np.eye(dims, dtype=dtype)]*components),
input_output_cholesky=True),
reinterpreted_batch_ndims=1),
s=lambda mix_probs, loc, precision: tfd.Sample(tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(probs=mix_probs),
components_distribution=MVNCholPrecisionTriL(
loc=loc,
chol_precision_tril=precision)),
sample_shape=num_samples)
))
def joint_log_prob(observations, mix_probs, loc, chol_precision):
"""BGMM with priors: loc=Normal, precision=Inverse-Wishart, mix=Dirichlet.
Args:
observations: `[n, d]`-shaped `Tensor` representing Bayesian Gaussian
Mixture model draws. Each sample is a length-`d` vector.
mix_probs: `[K]`-shaped `Tensor` representing random draw from
`Dirichlet` prior.
loc: `[K, d]`-shaped `Tensor` representing the location parameter of the
`K` components.
chol_precision: `[K, d, d]`-shaped `Tensor` representing `K` lower
triangular `cholesky(Precision)` matrices, each being sampled from
a Wishart distribution.
Returns:
log_prob: `Tensor` representing joint log-density over all inputs.
"""
return bgmm.log_prob(
mix_probs=mix_probs, loc=loc, precision=chol_precision, s=observations)
Wygeneruj dane „Treningu”
W tym demo spróbujemy losowych danych.
true_loc = np.array([[-2., -2],
[0, 0],
[2, 2]], dtype)
random = np.random.RandomState(seed=43)
true_hidden_component = random.randint(0, components, num_samples)
observations = (true_loc[true_hidden_component] +
random.randn(num_samples, dims).astype(dtype))
Wnioskowanie bayesowskie przy użyciu konsoli HMC
Teraz, gdy użyliśmy TFD do określenia naszego modelu i uzyskaliśmy pewne zaobserwowane dane, mamy wszystkie niezbędne elementy do uruchomienia HMC.
Aby to zrobić, użyjemy częściowe zastosowanie do „pin down” rzeczy, które nie chcą próbki. W tym przypadku oznacza, że potrzebujemy tylko przypiąć dół observations . (Hiper-parametry są już piecze się do stanu rozkładu, a nie część joint_log_prob podpisu funkcji).
unnormalized_posterior_log_prob = functools.partial(joint_log_prob, observations)
initial_state = [
tf.fill([components],
value=np.array(1. / components, dtype),
name='mix_probs'),
tf.constant(np.array([[-2., -2],
[0, 0],
[2, 2]], dtype),
name='loc'),
tf.linalg.eye(dims, batch_shape=[components], dtype=dtype, name='chol_precision'),
]
Nieograniczona reprezentacja
Hamiltonian Monte Carlo (HMC) wymaga, aby funkcja logarytmu docelowego była różniczkowalna ze względu na swoje argumenty. Co więcej, HMC może wykazywać znacznie wyższą wydajność statystyczną, jeśli przestrzeń stanów jest nieograniczona.
Oznacza to, że podczas pobierania próbek z tyłu BGMM będziemy musieli rozwiązać dwa główne problemy:
- \(\theta\) reprezentuje dyskretne prawdopodobieństwa wektor, czyli musi być taki, aby \(\sum_{k=1}^K \theta_k = 1\) i \(\theta_k>0\).
- \(T_k\) stanowi odwrotność macierzy kowariancji, to znaczy musi być tak \(T_k \succ 0\), to jest pozytyw określony .
Aby spełnić ten wymóg, musimy:
- przekształcić ograniczone zmienne w nieograniczoną przestrzeń
- uruchom MCMC w nieograniczonej przestrzeni
- przekształć nieograniczone zmienne z powrotem do ograniczonej przestrzeni.
Jak z MVNCholPrecisionTriL użyjemy Bijector s do transformacji zmiennych losowych do nieograniczonej przestrzeni.
Dirichletprzekształca się w swobodnej przestrzeni za pomocą funkcji Softmax .Nasza zmienna losowa precyzji jest rozkładem na dodatnich półokreślonych macierzach. Aby odblokuj nich użyjemy
FillTriangulariTransformDiagonalbijectors. Przekształcają one wektory w macierze dolnego trójkąta i zapewniają, że przekątna jest dodatnia. Były to przydatne, ponieważ umożliwia próbkowanie jedynie \(d(d+1)/2\) pływaków zamiast \(d^2\).
unconstraining_bijectors = [
tfb.SoftmaxCentered(),
tfb.Identity(),
tfb.Chain([
tfb.TransformDiagonal(tfb.Softplus()),
tfb.FillTriangular(),
])]
@tf.function(autograph=False)
def sample():
return tfp.mcmc.sample_chain(
num_results=2000,
num_burnin_steps=500,
current_state=initial_state,
kernel=tfp.mcmc.SimpleStepSizeAdaptation(
tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior_log_prob,
step_size=0.065,
num_leapfrog_steps=5),
bijector=unconstraining_bijectors),
num_adaptation_steps=400),
trace_fn=lambda _, pkr: pkr.inner_results.inner_results.is_accepted)
[mix_probs, loc, chol_precision], is_accepted = sample()
Teraz wykonamy łańcuch i wydrukujemy tylne środki.
acceptance_rate = tf.reduce_mean(tf.cast(is_accepted, dtype=tf.float32)).numpy()
mean_mix_probs = tf.reduce_mean(mix_probs, axis=0).numpy()
mean_loc = tf.reduce_mean(loc, axis=0).numpy()
mean_chol_precision = tf.reduce_mean(chol_precision, axis=0).numpy()
precision = tf.linalg.matmul(chol_precision, chol_precision, transpose_b=True)
print('acceptance_rate:', acceptance_rate)
print('avg mix probs:', mean_mix_probs)
print('avg loc:\n', mean_loc)
print('avg chol(precision):\n', mean_chol_precision)
acceptance_rate: 0.5305 avg mix probs: [0.25248723 0.60729516 0.1402176 ] avg loc: [[-1.96466753 -2.12047249] [ 0.27628865 0.22944732] [ 2.06461244 2.54216122]] avg chol(precision): [[[ 1.05105032 0. ] [ 0.12699955 1.06553113]] [[ 0.76058015 0. ] [-0.50332767 0.77947431]] [[ 1.22770457 0. ] [ 0.70670027 1.50914164]]]
loc_ = loc.numpy()
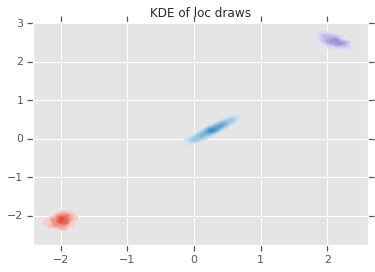
ax = sns.kdeplot(loc_[:,0,0], loc_[:,0,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,1,0], loc_[:,1,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,2,0], loc_[:,2,1], shade=True, shade_lowest=False)
plt.title('KDE of loc draws');
Wniosek
Ta prosta współpraca zademonstrowała, w jaki sposób prymitywy TensorFlow Probability można wykorzystać do budowania hierarchicznych modeli mieszanin bayesowskich.
