 TensorFlow.org पर देखें TensorFlow.org पर देखें |  Google Colab में चलाएं Google Colab में चलाएं |  GitHub पर स्रोत देखें GitHub पर स्रोत देखें |  नोटबुक डाउनलोड करें नोटबुक डाउनलोड करें |
इस कोलाब में हम केवल TensorFlow प्रायिकता प्रिमिटिव का उपयोग करके बायेसियन गॉसियन मिक्सचर मॉडल (BGMM) के पीछे से सैंपलिंग का पता लगाएंगे।
नमूना
के लिए \(k\in\{1,\ldots, K\}\) मिश्रण घटकों आयाम से प्रत्येक \(D\), हम मॉडल करना चाहते हैं \(i\in\{1,\ldots,N\}\) आईआईडी निम्नलिखित बायेसियन गाऊसी मिश्रण मॉडल का उपयोग कर नमूने:
\[\begin{align*} \theta &\sim \text{Dirichlet}(\text{concentration}=\alpha_0)\\ \mu_k &\sim \text{Normal}(\text{loc}=\mu_{0k}, \text{scale}=I_D)\\ T_k &\sim \text{Wishart}(\text{df}=5, \text{scale}=I_D)\\ Z_i &\sim \text{Categorical}(\text{probs}=\theta)\\ Y_i &\sim \text{Normal}(\text{loc}=\mu_{z_i}, \text{scale}=T_{z_i}^{-1/2})\\ \end{align*}\]
ध्यान दें, scale तर्क सभी cholesky अर्थ विज्ञान। हम इस कन्वेंशन का उपयोग करते हैं क्योंकि यह TF डिस्ट्रीब्यूशन का है (जो स्वयं इस कन्वेंशन का उपयोग आंशिक रूप से करता है क्योंकि यह कम्प्यूटेशनल रूप से लाभप्रद है)।
हमारा लक्ष्य पश्च से नमूने उत्पन्न करना है:
\[p\left(\theta, \{\mu_k, T_k\}_{k=1}^K \Big| \{y_i\}_{i=1}^N, \alpha_0, \{\mu_{ok}\}_{k=1}^K\right)\]
सूचना है कि \(\{Z_i\}_{i=1}^N\) मौजूद नहीं है - केवल उन यादृच्छिक परिवर्तनीय जिसके साथ पैमाने पर नहीं है में रुचि रखने वाले हम के \(N\)। (और सौभाग्य से वहाँ एक TF वितरण जो बाहर दरकिनार संभालती है \(Z_i\)।)
कम्प्यूटेशनल रूप से अट्रैक्टिव नॉर्मलाइज़ेशन टर्म के कारण इस वितरण से सीधे नमूना लेना संभव नहीं है।
महानगरों-हेस्टिंग्स एल्गोरिदम असभ्य करने वाली सामान्य वितरण से नमूने के लिए के लिए तकनीक है।
TensorFlow Probability कई MCMC विकल्प प्रदान करती है, जिनमें से कई मेट्रोपोलिस-हेस्टिंग्स पर आधारित हैं। इस नोटबुक में, हम इस्तेमाल करेंगे Hamiltonian मोंटे कार्लो ( tfp.mcmc.HamiltonianMonteCarlo )। एचएमसी अक्सर एक अच्छा विकल्प होता है क्योंकि यह तेजी से अभिसरण कर सकता है, संयुक्त रूप से राज्य स्थान का नमूना लेता है (समन्वय के विपरीत), और टीएफ के गुणों में से एक का लाभ उठाता है: स्वचालित भेदभाव। जिसके अनुसार, एक BGMM पीछे से नमूने वास्तव में बेहतर अन्य तरीकों, जैसे, के द्वारा किया जा सकता है गिब का नमूना ।
%matplotlib inline
import functools
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import seaborn as sns; sns.set_context('notebook')
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
physical_devices = tf.config.experimental.list_physical_devices('GPU')
if len(physical_devices) > 0:
tf.config.experimental.set_memory_growth(physical_devices[0], True)
वास्तव में मॉडल बनाने से पहले, हमें एक नए प्रकार के वितरण को परिभाषित करने की आवश्यकता होगी। ऊपर दिए गए मॉडल विनिर्देश से, यह स्पष्ट है कि हम एमवीएन को व्युत्क्रम सहप्रसरण मैट्रिक्स, यानी [सटीक मैट्रिक्स](https://en.wikipedia.org/wiki/Precision_(statistics%29) के साथ पैरामीटराइज़ कर रहे हैं। इसे इसमें पूरा करने के लिए TF, हम अपने शुरू करने की आवश्यकता होगी Bijector यह। Bijector आगे परिवर्तन का उपयोग करेगा:
-
Y = tf.linalg.triangular_solve((tf.linalg.matrix_transpose(chol_precision_tril), X, adjoint=True) + loc।
और log_prob गणना सिर्फ उलटा, यानी है:
-
X = tf.linalg.matmul(chol_precision_tril, X - loc, adjoint_a=True)।
के बाद से एच एम सी के लिए हम सभी की जरूरत है log_prob , इस का मतलब है कि हम कभी बुला से बचने tf.linalg.triangular_solve (के रूप में के लिए मामला होगा tfd.MultivariateNormalTriL )। यह लाभप्रद के बाद से है tf.linalg.matmul आमतौर पर तेजी से बेहतर कैश इलाके के कारण किया गया है।
class MVNCholPrecisionTriL(tfd.TransformedDistribution):
"""MVN from loc and (Cholesky) precision matrix."""
def __init__(self, loc, chol_precision_tril, name=None):
super(MVNCholPrecisionTriL, self).__init__(
distribution=tfd.Independent(tfd.Normal(tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=chol_precision_tril,
adjoint=True)),
]),
name=name)
tfd.Independent वितरण बदल जाता है स्वतंत्र एक वितरण का ड्रॉ, सांख्यिकीय स्वतंत्र निर्देशांक के साथ एक मल्टीवेरिएट वितरण में। कंप्यूटिंग के संदर्भ में log_prob , घटना आयाम (रों) के ऊपर एक सरल राशि के रूप में इस "मेटा-वितरण" प्रकट होता है।
यह भी ध्यान दें कि हम ले लिया adjoint पैमाने मैट्रिक्स के ( "पक्षांतरित")। इसका कारण यह है परिशुद्धता उलटा सहप्रसरण, यानी, अगर \(P=C^{-1}\) और अगर \(C=AA^\top\), तो \(P=BB^{\top}\) जहां \(B=A^{-\top}\)।
चूंकि यह वितरण मुश्किल की तरह है, जल्दी से सत्यापित करें कि हमारे जाने MVNCholPrecisionTriL काम करता है के रूप में हमें लगता है कि यह होना चाहिए।
def compute_sample_stats(d, seed=42, n=int(1e6)):
x = d.sample(n, seed=seed)
sample_mean = tf.reduce_mean(x, axis=0, keepdims=True)
s = x - sample_mean
sample_cov = tf.linalg.matmul(s, s, adjoint_a=True) / tf.cast(n, s.dtype)
sample_scale = tf.linalg.cholesky(sample_cov)
sample_mean = sample_mean[0]
return [
sample_mean,
sample_cov,
sample_scale,
]
dtype = np.float32
true_loc = np.array([1., -1.], dtype=dtype)
true_chol_precision = np.array([[1., 0.],
[2., 8.]],
dtype=dtype)
true_precision = np.matmul(true_chol_precision, true_chol_precision.T)
true_cov = np.linalg.inv(true_precision)
d = MVNCholPrecisionTriL(
loc=true_loc,
chol_precision_tril=true_chol_precision)
[sample_mean, sample_cov, sample_scale] = [
t.numpy() for t in compute_sample_stats(d)]
print('true mean:', true_loc)
print('sample mean:', sample_mean)
print('true cov:\n', true_cov)
print('sample cov:\n', sample_cov)
true mean: [ 1. -1.] sample mean: [ 1.0002806 -1.000105 ] true cov: [[ 1.0625 -0.03125 ] [-0.03125 0.015625]] sample cov: [[ 1.0641273 -0.03126175] [-0.03126175 0.01559312]]
चूंकि नमूना माध्य और सहप्रसरण वास्तविक माध्य और सहप्रसरण के करीब हैं, ऐसा लगता है कि वितरण सही ढंग से लागू किया गया है। अब, हम इस्तेमाल करेंगे MVNCholPrecisionTriL tfp.distributions.JointDistributionNamed BGMM मॉडल निर्दिष्ट करने के लिए। अवलोकन मॉडल के लिए, हम इस्तेमाल करेंगे tfd.MixtureSameFamily स्वचालित रूप से बाहर एकीकृत करने के लिए \(\{Z_i\}_{i=1}^N\) खींचता है।
dtype = np.float64
dims = 2
components = 3
num_samples = 1000
bgmm = tfd.JointDistributionNamed(dict(
mix_probs=tfd.Dirichlet(
concentration=np.ones(components, dtype) / 10.),
loc=tfd.Independent(
tfd.Normal(
loc=np.stack([
-np.ones(dims, dtype),
np.zeros(dims, dtype),
np.ones(dims, dtype),
]),
scale=tf.ones([components, dims], dtype)),
reinterpreted_batch_ndims=2),
precision=tfd.Independent(
tfd.WishartTriL(
df=5,
scale_tril=np.stack([np.eye(dims, dtype=dtype)]*components),
input_output_cholesky=True),
reinterpreted_batch_ndims=1),
s=lambda mix_probs, loc, precision: tfd.Sample(tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(probs=mix_probs),
components_distribution=MVNCholPrecisionTriL(
loc=loc,
chol_precision_tril=precision)),
sample_shape=num_samples)
))
def joint_log_prob(observations, mix_probs, loc, chol_precision):
"""BGMM with priors: loc=Normal, precision=Inverse-Wishart, mix=Dirichlet.
Args:
observations: `[n, d]`-shaped `Tensor` representing Bayesian Gaussian
Mixture model draws. Each sample is a length-`d` vector.
mix_probs: `[K]`-shaped `Tensor` representing random draw from
`Dirichlet` prior.
loc: `[K, d]`-shaped `Tensor` representing the location parameter of the
`K` components.
chol_precision: `[K, d, d]`-shaped `Tensor` representing `K` lower
triangular `cholesky(Precision)` matrices, each being sampled from
a Wishart distribution.
Returns:
log_prob: `Tensor` representing joint log-density over all inputs.
"""
return bgmm.log_prob(
mix_probs=mix_probs, loc=loc, precision=chol_precision, s=observations)
"प्रशिक्षण" डेटा उत्पन्न करें
इस डेमो के लिए, हम कुछ यादृच्छिक डेटा का नमूना लेंगे।
true_loc = np.array([[-2., -2],
[0, 0],
[2, 2]], dtype)
random = np.random.RandomState(seed=43)
true_hidden_component = random.randint(0, components, num_samples)
observations = (true_loc[true_hidden_component] +
random.randn(num_samples, dims).astype(dtype))
HMC . का उपयोग करते हुए बायेसियन अनुमान
अब जब हमने अपने मॉडल को निर्दिष्ट करने के लिए टीएफडी का उपयोग किया है और कुछ अवलोकन किए गए डेटा प्राप्त किए हैं, तो हमारे पास एचएमसी चलाने के लिए सभी आवश्यक टुकड़े हैं।
ऐसा करने के लिए, हम एक का उपयोग करेंगे आंशिक आवेदन "नीचे पिन" बातें हम नमूना नहीं करना चाहती है। इस मामले में साधन हम केवल नीचे पिन की जरूरत है कि observations । (हाइपर-पैरामीटर पहले से ही पिछले वितरण और का हिस्सा नहीं करने में पकाया जाता है joint_log_prob समारोह हस्ताक्षर।)
unnormalized_posterior_log_prob = functools.partial(joint_log_prob, observations)
initial_state = [
tf.fill([components],
value=np.array(1. / components, dtype),
name='mix_probs'),
tf.constant(np.array([[-2., -2],
[0, 0],
[2, 2]], dtype),
name='loc'),
tf.linalg.eye(dims, batch_shape=[components], dtype=dtype, name='chol_precision'),
]
अप्रतिबंधित प्रतिनिधित्व
हैमिल्टनियन मोंटे कार्लो (HMC) को लक्ष्य लॉग-प्रायिकता फ़ंक्शन को अपने तर्कों के संबंध में अलग-अलग करने की आवश्यकता है। इसके अलावा, एचएमसी नाटकीय रूप से उच्च सांख्यिकीय दक्षता प्रदर्शित कर सकता है यदि राज्य-स्थान अप्रतिबंधित है।
इसका मतलब है कि बीजीएमएम पोस्टीरियर से नमूना लेते समय हमें दो मुख्य मुद्दों पर काम करना होगा:
- \(\theta\) यानी, एक असतत संभावना वेक्टर का प्रतिनिधित्व करता है, इस तरह के होना चाहिए कि \(\sum_{k=1}^K \theta_k = 1\) और \(\theta_k>0\)।
- \(T_k\) का प्रतिनिधित्व करता है एक व्युत्क्रम सहप्रसरण मैट्रिक्स, यानी, ऐसी है कि होना चाहिए \(T_k \succ 0\), यानी, है सकारात्मक निश्चित ।
इस आवश्यकता को पूरा करने के लिए हमें यह करना होगा:
- विवश चर को एक अप्रतिबंधित स्थान में बदलना
- एमसीएमसी को अबाधित जगह पर चलाएं
- अप्रतिबंधित चर को वापस विवश स्थान में बदलना।
साथ के रूप में MVNCholPrecisionTriL , हम उपयोग करेंगे Bijector रों स्वेच्छापूर्ण अंतरिक्ष के लिए यादृच्छिक परिवर्तनीय को बदलने के लिए।
Dirichletके माध्यम से स्वेच्छापूर्ण अंतरिक्ष के लिए तब्दील हो जाता है softmax समारोह ।हमारा सटीक यादृच्छिक चर पोस्टिव सेमीडेफिनिट मैट्रिसेस पर एक वितरण है। इन को अबाधित करने के लिए हम इस्तेमाल करेंगे
FillTriangularऔरTransformDiagonalbijectors। ये वैक्टर को निचले-त्रिकोणीय मैट्रिक्स में परिवर्तित करते हैं और सुनिश्चित करते हैं कि विकर्ण सकारात्मक है। क्योंकि यह सक्षम केवल नमूने पूर्व उपयोगी है \(d(d+1)/2\) बजाय तैरता \(d^2\)।
unconstraining_bijectors = [
tfb.SoftmaxCentered(),
tfb.Identity(),
tfb.Chain([
tfb.TransformDiagonal(tfb.Softplus()),
tfb.FillTriangular(),
])]
@tf.function(autograph=False)
def sample():
return tfp.mcmc.sample_chain(
num_results=2000,
num_burnin_steps=500,
current_state=initial_state,
kernel=tfp.mcmc.SimpleStepSizeAdaptation(
tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior_log_prob,
step_size=0.065,
num_leapfrog_steps=5),
bijector=unconstraining_bijectors),
num_adaptation_steps=400),
trace_fn=lambda _, pkr: pkr.inner_results.inner_results.is_accepted)
[mix_probs, loc, chol_precision], is_accepted = sample()
अब हम श्रृंखला को क्रियान्वित करेंगे और पीछे के साधनों को प्रिंट करेंगे।
acceptance_rate = tf.reduce_mean(tf.cast(is_accepted, dtype=tf.float32)).numpy()
mean_mix_probs = tf.reduce_mean(mix_probs, axis=0).numpy()
mean_loc = tf.reduce_mean(loc, axis=0).numpy()
mean_chol_precision = tf.reduce_mean(chol_precision, axis=0).numpy()
precision = tf.linalg.matmul(chol_precision, chol_precision, transpose_b=True)
print('acceptance_rate:', acceptance_rate)
print('avg mix probs:', mean_mix_probs)
print('avg loc:\n', mean_loc)
print('avg chol(precision):\n', mean_chol_precision)
acceptance_rate: 0.5305 avg mix probs: [0.25248723 0.60729516 0.1402176 ] avg loc: [[-1.96466753 -2.12047249] [ 0.27628865 0.22944732] [ 2.06461244 2.54216122]] avg chol(precision): [[[ 1.05105032 0. ] [ 0.12699955 1.06553113]] [[ 0.76058015 0. ] [-0.50332767 0.77947431]] [[ 1.22770457 0. ] [ 0.70670027 1.50914164]]]
loc_ = loc.numpy()
ax = sns.kdeplot(loc_[:,0,0], loc_[:,0,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,1,0], loc_[:,1,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,2,0], loc_[:,2,1], shade=True, shade_lowest=False)
plt.title('KDE of loc draws');
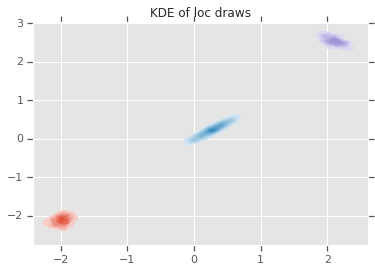
निष्कर्ष
इस सरल कोलाब ने प्रदर्शित किया कि कैसे TensorFlow प्रायिकता आदिम का उपयोग पदानुक्रमित बायेसियन मिश्रण मॉडल बनाने के लिए किया जा सकता है।
