 مشاهده در TensorFlow.org مشاهده در TensorFlow.org |  در Google Colab اجرا شود در Google Colab اجرا شود |  مشاهده منبع در GitHub مشاهده منبع در GitHub |  دانلود دفترچه یادداشت دانلود دفترچه یادداشت |
در این colab نمونه برداری از مدل مخلوط بیزی گاوسی (BGMM) را تنها با استفاده از احتمالات اولیه TensorFlow بررسی خواهیم کرد.
مدل
برای \(k\in\{1,\ldots, K\}\) اجزای مخلوط هر یک از ابعاد \(D\)، ما می خواهم به مدل دوست \(i\in\{1,\ldots,N\}\) IID نمونه با استفاده از زیر بیزی گاوسی مدل مخلوط:
\[\begin{align*} \theta &\sim \text{Dirichlet}(\text{concentration}=\alpha_0)\\ \mu_k &\sim \text{Normal}(\text{loc}=\mu_{0k}, \text{scale}=I_D)\\ T_k &\sim \text{Wishart}(\text{df}=5, \text{scale}=I_D)\\ Z_i &\sim \text{Categorical}(\text{probs}=\theta)\\ Y_i &\sim \text{Normal}(\text{loc}=\mu_{z_i}, \text{scale}=T_{z_i}^{-1/2})\\ \end{align*}\]
توجه داشته باشید، scale استدلال همه cholesky معناشناسی. ما از این قرارداد استفاده می کنیم زیرا این قرارداد مربوط به توزیع های TF است (که خود تا حدی از این قرارداد استفاده می کند زیرا از نظر محاسباتی سودمند است).
هدف ما این است که نمونههایی را از پسین تولید کنیم:
\[p\left(\theta, \{\mu_k, T_k\}_{k=1}^K \Big| \{y_i\}_{i=1}^N, \alpha_0, \{\mu_{ok}\}_{k=1}^K\right)\]
توجه داشته باشید که \(\{Z_i\}_{i=1}^N\) وجود ندارد - در تنها آن دسته از متغیرهای تصادفی که با مقیاس نیست علاقه مند ما در حال \(N\). (و خوشبختانه یک توزیع TF که دسته به حاشیه راندن در خارج وجود دارد \(Z_i\).)
به دلیل یک عبارت عادی سازی محاسباتی غیرقابل حل، امکان نمونه گیری مستقیم از این توزیع وجود ندارد.
الگوریتم های کلانشهر-هیستینگز هستند تکنیک برای نمونه برداری از توزیع های مقاوم به عادی.
TensorFlow Probability تعدادی گزینه MCMC را ارائه می دهد، از جمله چندین گزینه بر اساس Metropolis-Hastings. در این نوت بوک، ما استفاده از هامیلتونی مونت کارلو ( tfp.mcmc.HamiltonianMonteCarlo ). HMC اغلب انتخاب خوبی است زیرا می تواند به سرعت همگرا شود، فضای حالت را به طور مشترک نمونه برداری می کند (بر خلاف هماهنگی)، و از یکی از مزایای TF استفاده می کند: تمایز خودکار. که گفت، نمونه برداری از یک خلفی BGMM ممکن است در واقع است بهتر است با روش های دیگر، به عنوان مثال، انجام نمونه برداری گیب است .
%matplotlib inline
import functools
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import seaborn as sns; sns.set_context('notebook')
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
physical_devices = tf.config.experimental.list_physical_devices('GPU')
if len(physical_devices) > 0:
tf.config.experimental.set_memory_growth(physical_devices[0], True)
قبل از ساختن مدل، باید نوع جدیدی از توزیع را تعریف کنیم. از مشخصات مدل بالا، واضح است که ما MVN را با یک ماتریس کوواریانس معکوس، یعنی [ماتریس دقیق] (https://en.wikipedia.org/wiki/Precision_(statistics%29) پارامتر می کنیم. برای انجام این کار در TF، ما باید به رول از ما Bijector این. Bijector خواهد تحول رو به جلو استفاده کنید:
-
Y = tf.linalg.triangular_solve((tf.linalg.matrix_transpose(chol_precision_tril), X, adjoint=True) + loc.
و log_prob محاسبه فقط معکوس است، یعنی:
-
X = tf.linalg.matmul(chol_precision_tril, X - loc, adjoint_a=True).
از آنجا که همه نیاز ما برای شورای عالی رسانه ها است log_prob ، این بدان معنی اجتناب از ما تا به حال خواستار tf.linalg.triangular_solve (به عنوان می شود در مورد tfd.MultivariateNormalTriL ). این به نفع است زیرا tf.linalg.matmul است که معمولا سریع تر به محل کش بهتر به علت.
class MVNCholPrecisionTriL(tfd.TransformedDistribution):
"""MVN from loc and (Cholesky) precision matrix."""
def __init__(self, loc, chol_precision_tril, name=None):
super(MVNCholPrecisionTriL, self).__init__(
distribution=tfd.Independent(tfd.Normal(tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=chol_precision_tril,
adjoint=True)),
]),
name=name)
tfd.Independent مستقل نوبت توزیع تساوی یک توزیع، به یک توزیع چند متغیره با مختصات آماری مستقل. از لحاظ محاسباتی log_prob ، این "متا توزیع کنندگان" آشکار به عنوان یک جمع ساده بیش از ابعاد رویداد (ها).
همچنین توجه کنید که ما در زمان adjoint ( "ترانهاده") از ماتریس مقیاس. دلیل این است که اگر دقت کوواریانس معکوس، یعنی \(P=C^{-1}\) و اگر \(C=AA^\top\)، سپس \(P=BB^{\top}\) که در آن \(B=A^{-\top}\).
از آنجا که این توزیع است نوع حیله و تزویر، اجازه دهید به سرعت بررسی کنید که ما MVNCholPrecisionTriL کار می کند به عنوان ما فکر می کنیم که باید.
def compute_sample_stats(d, seed=42, n=int(1e6)):
x = d.sample(n, seed=seed)
sample_mean = tf.reduce_mean(x, axis=0, keepdims=True)
s = x - sample_mean
sample_cov = tf.linalg.matmul(s, s, adjoint_a=True) / tf.cast(n, s.dtype)
sample_scale = tf.linalg.cholesky(sample_cov)
sample_mean = sample_mean[0]
return [
sample_mean,
sample_cov,
sample_scale,
]
dtype = np.float32
true_loc = np.array([1., -1.], dtype=dtype)
true_chol_precision = np.array([[1., 0.],
[2., 8.]],
dtype=dtype)
true_precision = np.matmul(true_chol_precision, true_chol_precision.T)
true_cov = np.linalg.inv(true_precision)
d = MVNCholPrecisionTriL(
loc=true_loc,
chol_precision_tril=true_chol_precision)
[sample_mean, sample_cov, sample_scale] = [
t.numpy() for t in compute_sample_stats(d)]
print('true mean:', true_loc)
print('sample mean:', sample_mean)
print('true cov:\n', true_cov)
print('sample cov:\n', sample_cov)
true mean: [ 1. -1.] sample mean: [ 1.0002806 -1.000105 ] true cov: [[ 1.0625 -0.03125 ] [-0.03125 0.015625]] sample cov: [[ 1.0641273 -0.03126175] [-0.03126175 0.01559312]]
از آنجایی که میانگین و کوواریانس نمونه به میانگین و کوواریانس واقعی نزدیک است، به نظر می رسد توزیع به درستی اجرا شده است. حال حاضر، ما استفاده از MVNCholPrecisionTriL tfp.distributions.JointDistributionNamed برای مشخص کردن مدل BGMM. برای مدل های مشاهده، ما استفاده از tfd.MixtureSameFamily به طور خودکار ادغام کردن \(\{Z_i\}_{i=1}^N\) تساوی.
dtype = np.float64
dims = 2
components = 3
num_samples = 1000
bgmm = tfd.JointDistributionNamed(dict(
mix_probs=tfd.Dirichlet(
concentration=np.ones(components, dtype) / 10.),
loc=tfd.Independent(
tfd.Normal(
loc=np.stack([
-np.ones(dims, dtype),
np.zeros(dims, dtype),
np.ones(dims, dtype),
]),
scale=tf.ones([components, dims], dtype)),
reinterpreted_batch_ndims=2),
precision=tfd.Independent(
tfd.WishartTriL(
df=5,
scale_tril=np.stack([np.eye(dims, dtype=dtype)]*components),
input_output_cholesky=True),
reinterpreted_batch_ndims=1),
s=lambda mix_probs, loc, precision: tfd.Sample(tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(probs=mix_probs),
components_distribution=MVNCholPrecisionTriL(
loc=loc,
chol_precision_tril=precision)),
sample_shape=num_samples)
))
def joint_log_prob(observations, mix_probs, loc, chol_precision):
"""BGMM with priors: loc=Normal, precision=Inverse-Wishart, mix=Dirichlet.
Args:
observations: `[n, d]`-shaped `Tensor` representing Bayesian Gaussian
Mixture model draws. Each sample is a length-`d` vector.
mix_probs: `[K]`-shaped `Tensor` representing random draw from
`Dirichlet` prior.
loc: `[K, d]`-shaped `Tensor` representing the location parameter of the
`K` components.
chol_precision: `[K, d, d]`-shaped `Tensor` representing `K` lower
triangular `cholesky(Precision)` matrices, each being sampled from
a Wishart distribution.
Returns:
log_prob: `Tensor` representing joint log-density over all inputs.
"""
return bgmm.log_prob(
mix_probs=mix_probs, loc=loc, precision=chol_precision, s=observations)
داده های "آموزش" را تولید کنید
برای این نسخه ی نمایشی، برخی از داده های تصادفی را نمونه برداری می کنیم.
true_loc = np.array([[-2., -2],
[0, 0],
[2, 2]], dtype)
random = np.random.RandomState(seed=43)
true_hidden_component = random.randint(0, components, num_samples)
observations = (true_loc[true_hidden_component] +
random.randn(num_samples, dims).astype(dtype))
استنتاج بیزی با استفاده از HMC
اکنون که از TFD برای مشخص کردن مدل خود استفاده کرده ایم و برخی داده های مشاهده شده را به دست آورده ایم، تمام قطعات لازم برای اجرای HMC را داریم.
برای انجام این کار، ما یک با استفاده از نرم افزار جزئی به "پین کردن" چیزهایی که ما به نمونه را نمی خواهم. در این مورد بدان معناست که ما تنها نیاز به پین کردن observations . (بیش از حد پارامترهای در حال حاضر در به توزیع قبل و نه بخشی از پخته joint_log_prob تابع امضا.)
unnormalized_posterior_log_prob = functools.partial(joint_log_prob, observations)
initial_state = [
tf.fill([components],
value=np.array(1. / components, dtype),
name='mix_probs'),
tf.constant(np.array([[-2., -2],
[0, 0],
[2, 2]], dtype),
name='loc'),
tf.linalg.eye(dims, batch_shape=[components], dtype=dtype, name='chol_precision'),
]
بازنمایی بدون محدودیت
همیلتونی مونت کارلو (HMC) مستلزم آن است که تابع log-probability هدف با توجه به آرگومان هایش قابل تمایز باشد. علاوه بر این، HMC میتواند کارایی آماری بهطور چشمگیری بالاتری از خود نشان دهد اگر فضای حالت نامحدود باشد.
این بدان معناست که هنگام نمونه برداری از BGMM پسین، باید دو مسئله اصلی را حل کنیم:
- \(\theta\) نشان دهنده یک بردار احتمال گسسته، به عنوان مثال، باید به گونه ای باشد که \(\sum_{k=1}^K \theta_k = 1\) و \(\theta_k>0\).
- \(T_k\) نشان دهنده معکوس کوواریانس ماتریس، به عنوان مثال، باید به گونه ای که می شود \(T_k \succ 0\)، یعنی مثبت قطعی .
برای رفع این نیاز باید:
- متغیرهای محدود را به یک فضای نامحدود تبدیل کنید
- MCMC را در فضای نامحدود اجرا کنید
- متغیرهای نامحدود را به فضای محدود تبدیل می کند.
همانطور که با MVNCholPrecisionTriL ، ما استفاده از Bijector بازدید کنندگان برای تبدیل متغیرهای تصادفی به فضا نامحدود.
Dirichletبه فضای نامحدود از طریق تبدیل تابع softmax .متغیر تصادفی دقیق ما توزیعی بر روی ماتریس های نیمه معین مثبت است. برای unconstrain این خواهیم استفاده
FillTriangularوTransformDiagonalbijectors. این بردارها را به ماتریس های مثلثی پایین تبدیل می کند و از مثبت بودن قطر اطمینان می دهد. سابق مفید است زیرا قادر می سازد نمونه برداری تنها \(d(d+1)/2\) شناور به جای \(d^2\).
unconstraining_bijectors = [
tfb.SoftmaxCentered(),
tfb.Identity(),
tfb.Chain([
tfb.TransformDiagonal(tfb.Softplus()),
tfb.FillTriangular(),
])]
@tf.function(autograph=False)
def sample():
return tfp.mcmc.sample_chain(
num_results=2000,
num_burnin_steps=500,
current_state=initial_state,
kernel=tfp.mcmc.SimpleStepSizeAdaptation(
tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior_log_prob,
step_size=0.065,
num_leapfrog_steps=5),
bijector=unconstraining_bijectors),
num_adaptation_steps=400),
trace_fn=lambda _, pkr: pkr.inner_results.inner_results.is_accepted)
[mix_probs, loc, chol_precision], is_accepted = sample()
ما اکنون زنجیره را اجرا می کنیم و ابزار خلفی را چاپ می کنیم.
acceptance_rate = tf.reduce_mean(tf.cast(is_accepted, dtype=tf.float32)).numpy()
mean_mix_probs = tf.reduce_mean(mix_probs, axis=0).numpy()
mean_loc = tf.reduce_mean(loc, axis=0).numpy()
mean_chol_precision = tf.reduce_mean(chol_precision, axis=0).numpy()
precision = tf.linalg.matmul(chol_precision, chol_precision, transpose_b=True)
print('acceptance_rate:', acceptance_rate)
print('avg mix probs:', mean_mix_probs)
print('avg loc:\n', mean_loc)
print('avg chol(precision):\n', mean_chol_precision)
acceptance_rate: 0.5305 avg mix probs: [0.25248723 0.60729516 0.1402176 ] avg loc: [[-1.96466753 -2.12047249] [ 0.27628865 0.22944732] [ 2.06461244 2.54216122]] avg chol(precision): [[[ 1.05105032 0. ] [ 0.12699955 1.06553113]] [[ 0.76058015 0. ] [-0.50332767 0.77947431]] [[ 1.22770457 0. ] [ 0.70670027 1.50914164]]]
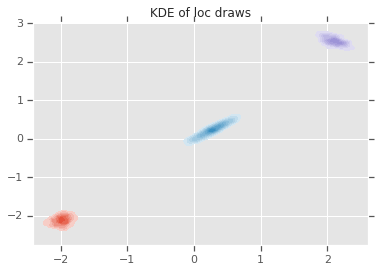
loc_ = loc.numpy()
ax = sns.kdeplot(loc_[:,0,0], loc_[:,0,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,1,0], loc_[:,1,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,2,0], loc_[:,2,1], shade=True, shade_lowest=False)
plt.title('KDE of loc draws');
نتیجه
این مجموعه ساده نشان داد که چگونه میتوان از روشهای بدوی احتمال TensorFlow برای ساخت مدلهای مخلوط بیزی سلسله مراتبی استفاده کرد.
