TensorFlow Kafesi (TFL)

TensorFlow Lattice, esnek, kontrollü ve yorumlanabilir kafes tabanlı modelleri uygulayan bir kütüphanedir. Kitaplık, sağduyuya dayalı veya politikaya dayalı şekil kısıtlamaları yoluyla alan bilgisini öğrenme sürecine eklemenizi sağlar. Bu, monotonluk, dışbükeylik ve ikili güven gibi kısıtlamaları karşılayabilen bir Keras katmanları koleksiyonu kullanılarak yapılır. Kütüphane aynı zamanda kurulumu kolay önceden hazırlanmış modeller de sağlar.

Kavramlar

Bu bölüm , Monotonik Kalibre Edilmiş Enterpolasyonlu Arama Tabloları , JMLR 2016'daki açıklamanın basitleştirilmiş bir versiyonudur.

Kafesler

Kafes, verilerinizdeki rastgele giriş-çıkış ilişkilerini yaklaşık olarak tahmin edebilen enterpolasyonlu bir arama tablosudur. Giriş alanınıza düzenli bir ızgarayı yerleştirir ve ızgaranın köşelerindeki çıktıya ilişkin değerleri öğrenir. Bir test noktası için \(x\), \(f(x)\) çevreleyen kafes değerlerinden doğrusal olarak enterpolasyon yapılır \(x\).

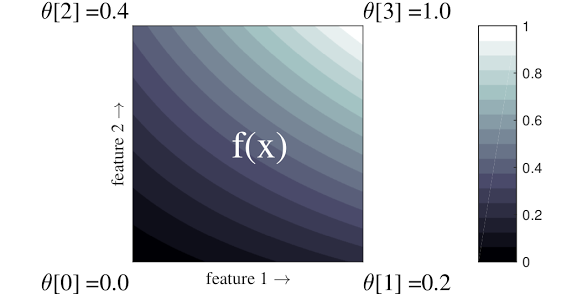
Yukarıdaki basit örnek, 2 giriş özelliğine ve 4 parametreye sahip bir fonksiyondur:\(\theta=[0, 0.2, 0.4, 1]\)bunlar giriş alanının köşelerindeki fonksiyonun değerleridir; fonksiyonun geri kalanı bu parametrelerden enterpolasyonla hesaplanır.

fonksiyon \(f(x)\) özellikler arasındaki doğrusal olmayan etkileşimleri yakalayabilir. Kafes parametrelerini, düzenli bir ızgara üzerinde zemine yerleştirilen direklerin yüksekliği olarak düşünebilirsiniz ve ortaya çıkan fonksiyon, dört direğe sıkıca çekilen kumaş gibidir.

İle \(D\) özellikler ve her boyut boyunca 2 köşe, düzenli bir kafese sahip olacaktır. \(2^D\) parametreler. Daha esnek bir işleve uyum sağlamak için, özellik alanı üzerinde her boyut boyunca daha fazla köşe içeren daha ince taneli bir kafes belirleyebilirsiniz. Kafes regresyon fonksiyonları süreklidir ve parçalı olarak sonsuz şekilde türevlenebilir.

Kalibrasyon

Diyelim ki önceki örnek kafes, aşağıdaki özellikler kullanılarak hesaplanan, önerilen bir yerel kafe ile öğrenilmiş bir kullanıcı mutluluğunu temsil ediyor:

  • kahve fiyatı, 0 ila 20 dolar aralığında
  • kullanıcıya uzaklık, 0 ila 30 kilometre aralığında

Modelimizin yerel bir kahvehane önerisiyle kullanıcı mutluluğunu öğrenmesini istiyoruz. TensorFlow Lattice modelleri, giriş özelliklerini kafes tarafından kabul edilen aralığa kalibre etmek ve normalleştirmek için parçalı doğrusal işlevleri ( tfl.layers.PWLCalibration ile) kullanabilir: yukarıdaki örnek kafeste 0,0 ila 1,0. Aşağıdaki örneklerde bu tür kalibrasyon fonksiyonlarının 10 anahtar noktayla gösterimi gösterilmektedir:

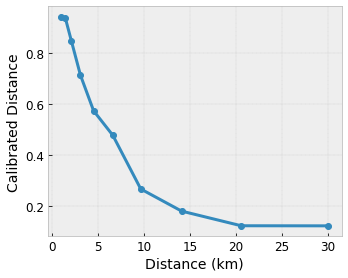
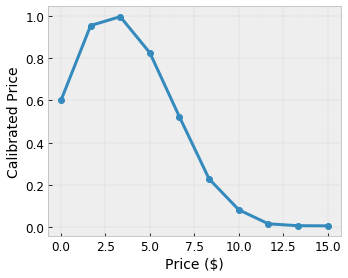
Özelliklerin yüzdelik dilimlerini giriş anahtar noktaları olarak kullanmak genellikle iyi bir fikirdir. TensorFlow Lattice'in önceden hazırlanmış modelleri, giriş anahtar noktalarını özellik miktarlarına otomatik olarak ayarlayabilir.

Kategorik özellikler için TensorFlow Lattice, bir kafesi beslemek üzere benzer çıktı sınırlamasıyla kategorik kalibrasyon ( tfl.layers.CategoricalCalibration ile) sağlar.

Topluluklar

Kafes katmanının parametre sayısı, giriş özelliklerinin sayısıyla birlikte üstel olarak artar, dolayısıyla çok yüksek boyutlara iyi ölçeklenemez. Bu sınırlamanın üstesinden gelmek için TensorFlow Lattice, birkaç küçük kafesi birleştiren (ortalama) kafes toplulukları sunar; bu, modelin özellik sayısında doğrusal olarak büyümesini sağlar.

Kütüphane bu toplulukların iki varyasyonunu sağlar:

  • Rastgele Küçük Kafesler (RTL): Her alt model, rastgele bir özellik alt kümesi kullanır (değiştirilmeli).

  • Kristaller : Kristaller algoritması ilk önce ikili özellik etkileşimlerini tahmin eden bir ön uydurma modelini eğitir. Daha sonra son topluluğu, daha fazla doğrusal olmayan etkileşime sahip özelliklerin aynı kafeslerde olacağı şekilde düzenler.

Neden TensorFlow Lattice?

Bu TF Blog yazısında TensorFlow Lattice'e kısa bir giriş bulabilirsiniz.

Yorumlanabilirlik

Her katmanın parametreleri o katmanın çıktısı olduğundan modelin her parçasını analiz etmek, anlamak ve hata ayıklamak kolaydır.

Doğru ve Esnek Modeller

İnce taneli kafesler kullanarak, tek bir kafes katmanıyla keyfi derecede karmaşık işlevler elde edebilirsiniz. Birden fazla kalibratör ve kafes katmanının kullanılması pratikte sıklıkla iyi çalışır ve benzer boyutlardaki DNN modelleriyle eşleşebilir veya onlardan daha iyi performans gösterebilir.

Sağduyu Şekil Kısıtlamaları

Gerçek dünyadaki eğitim verileri, çalışma zamanı verilerini yeterince temsil etmeyebilir. DNN'ler veya ormanlar gibi esnek makine öğrenimi çözümleri, giriş alanının eğitim verilerinin kapsamadığı kısımlarında genellikle beklenmedik ve hatta çılgınca hareket eder. Bu davranış özellikle politika veya adalet kısıtlamalarının ihlal edilebildiği durumlarda sorunludur.

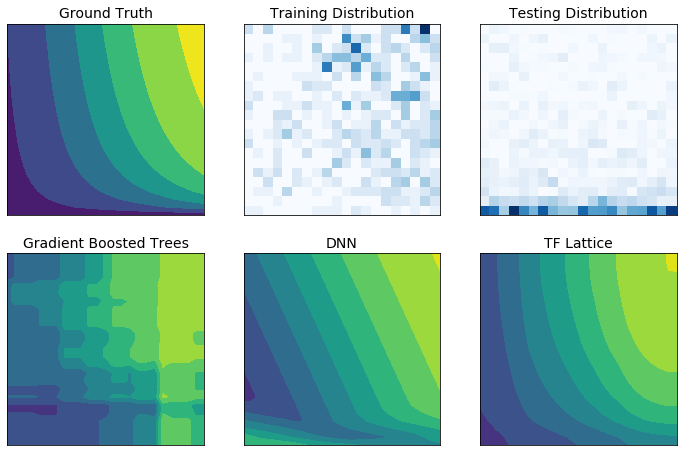
Yaygın düzenleme biçimleri daha mantıklı bir ekstrapolasyonla sonuçlanabilse de, standart düzenleyiciler, özellikle yüksek boyutlu girdilerle, tüm girdi alanı boyunca makul model davranışını garanti edemez. Daha kontrollü ve öngörülebilir davranışa sahip daha basit modellere geçiş, model doğruluğu açısından ciddi bir maliyet getirebilir.

TF Lattice, esnek modelleri kullanmaya devam etmeyi mümkün kılar, ancak anlamsal olarak anlamlı sağduyulu veya politika odaklı şekil kısıtlamaları aracılığıyla alan bilgisini öğrenme sürecine dahil etmek için çeşitli seçenekler sunar:

  • Monotonluk : Çıkışın yalnızca bir girişe göre artacağını/azalacağını belirtebilirsiniz. Örneğimizde, bir kafeye olan mesafenin artmasının yalnızca öngörülen kullanıcı tercihini azaltması gerektiğini belirtmek isteyebilirsiniz.

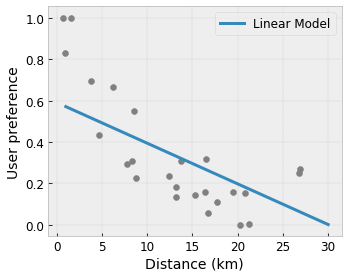
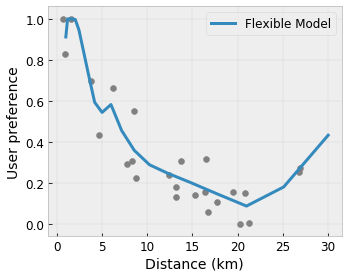
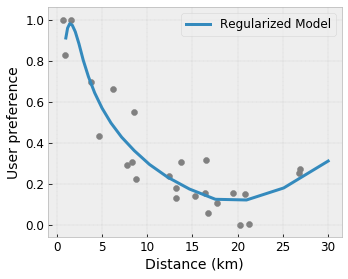
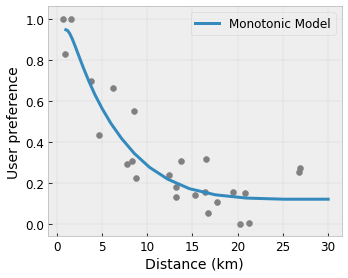
  • Dışbükey/İçbükey : Fonksiyon şeklinin dışbükey veya içbükey olabileceğini belirtebilirsiniz. Monotonlukla birleştiğinde bu durum, fonksiyonu belirli bir özelliğe göre azalan getirileri temsil etmeye zorlayabilir.

  • Tek modluluk : Fonksiyonun benzersiz bir zirveye veya benzersiz bir vadiye sahip olması gerektiğini belirtebilirsiniz. Bu, bir özelliğe göre tatlı bir noktaya sahip olan işlevleri temsil etmenizi sağlar.

  • Çift yönlü güven : Bu kısıtlama bir çift özellik üzerinde çalışır ve bir giriş özelliğinin anlamsal olarak başka bir özelliğe olan güveni yansıttığını öne sürer. Örneğin, daha fazla sayıda yorum almak, bir restoranın ortalama yıldız derecelendirmesine daha fazla güvenmenizi sağlar. İnceleme sayısı arttıkça model yıldız derecelendirmesine göre daha duyarlı olacaktır (yani derecelendirmeye göre daha büyük bir eğime sahip olacaktır).

Düzenleyicilerle Kontrollü Esneklik

Şekil kısıtlamalarına ek olarak TensorFlow kafesi, her katman için işlevin esnekliğini ve düzgünlüğünü kontrol etmek üzere bir dizi düzenleyici sağlar.

  • Laplace Düzenleyici : Kafes/kalibrasyon köşelerinin/anahtar noktalarının çıktıları, ilgili komşularının değerlerine göre düzenlenir. Bu daha düz bir işlevle sonuçlanır.

  • Hessian Düzenleyici : Bu, fonksiyonu daha doğrusal hale getirmek için PWL kalibrasyon katmanının ilk türevini cezalandırır.

  • Kırışıklık Düzenleyici : Bu, eğrilikteki ani değişiklikleri önlemek için PWL kalibrasyon katmanının ikinci türevini cezalandırır. Fonksiyonu daha pürüzsüz hale getirir.

  • Burulma Düzenleyici : Kafesin çıkışları, özellikler arasında burulmayı önleyecek şekilde düzenlenecektir. Başka bir deyişle model, özelliklerin katkıları arasında bağımsızlığa yönelik olarak düzenlenecektir.

Diğer Keras katmanlarıyla karıştırın ve eşleştirin

Kısmen kısıtlanmış veya düzenli modeller oluşturmak için TF Lattice katmanlarını diğer Keras katmanlarıyla birlikte kullanabilirsiniz. Örneğin, yerleştirmeleri veya diğer Keras katmanlarını içeren daha derin ağların son katmanında kafes veya PWL kalibrasyon katmanları kullanılabilir.

Makaleler

Öğreticiler ve API belgeleri

Yaygın model mimarileri için Keras'ın önceden hazırlanmış modellerini kullanabilirsiniz. Ayrıca TF Lattice Keras katmanlarını kullanarak özel modeller oluşturabilir veya diğer Keras katmanlarıyla karıştırıp eşleştirebilirsiniz. Ayrıntılar için API belgelerinin tamamına göz atın.