TensorFlow Lattice (TFL)

O TensorFlow Lattice é uma biblioteca que implementa modelos baseados em treliças flexíveis, controlados e interpretáveis. A biblioteca permite que você injete o conhecimento do domínio no processo de aprendizado por meio de restrições de forma baseadas no senso comum ou orientadas por políticas. Isso é feito usando uma coleção de camadas Keras que podem satisfazer restrições como monotonicidade, convexidade e confiança em pares. A biblioteca também fornece estimadores enlatados fáceis de configurar.

Conceitos

Esta seção é uma versão simplificada da descrição em Monotonic Calibrated Interpolated Look-Up Tables , JMLR 2016.

Treliças

Uma treliça é uma tabela de consulta interpolada que pode aproximar relações arbitrárias de entrada-saída em seus dados. Ele sobrepõe uma grade regular em seu espaço de entrada e aprende valores para a saída nos vértices da grade. Para um ponto de teste \(x\), \(f(x)\) é interpolado linearmente a partir dos valores de rede que cercam \(x\).

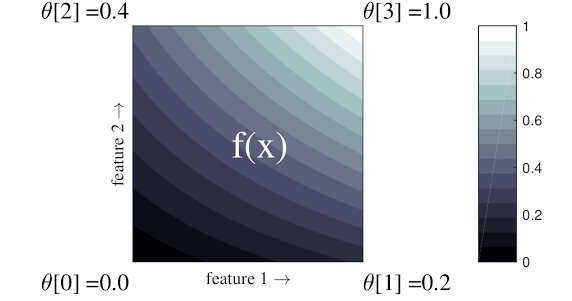
O exemplo simples acima é uma função com 2 recursos de entrada e 4 parâmetros:\(\theta=[0, 0.2, 0.4, 1]\), que são os valores da função nos cantos do espaço de entrada; o restante da função é interpolado a partir desses parâmetros.

A função \(f(x)\) pode capturar interações não lineares entre recursos. Você pode pensar nos parâmetros da treliça como a altura dos postes colocados no chão em uma grade regular, e a função resultante é como um pano apertado contra os quatro postes.

Com recursos \(D\) e 2 vértices ao longo de cada dimensão, uma rede regular terá parâmetros \(2^D\) . Para ajustar uma função mais flexível, você pode especificar uma rede mais fina sobre o espaço de recurso com mais vértices ao longo de cada dimensão. As funções de regressão de rede são contínuas e infinitamente diferenciáveis ​​por partes.

Calibração

Digamos que a estrutura de exemplo anterior represente a felicidade de um usuário aprendido com uma cafeteria local sugerida calculada usando recursos:

  • preço do café, na faixa de 0 a 20 dólares
  • distância até o usuário, na faixa de 0 a 30 quilômetros

Queremos que nosso modelo aprenda a felicidade do usuário com uma sugestão de cafeteria local. Os modelos do TensorFlow Lattice podem usar funções lineares por partes (com tfl.layers.PWLCalibration ) para calibrar e normalizar os recursos de entrada para o intervalo aceito pela treliça: 0,0 a 1,0 no exemplo de treliça acima. A seguir, exemplos de funções de calibração com 10 pontos-chave:

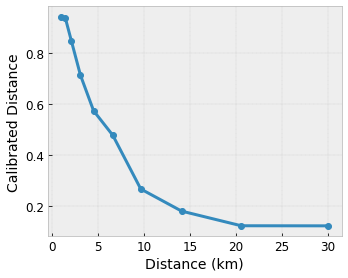
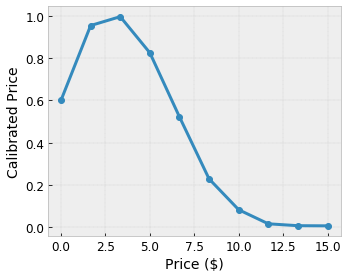
Muitas vezes, é uma boa ideia usar os quantis dos recursos como pontos-chave de entrada. Os estimadores enlatados do TensorFlow Lattice podem definir automaticamente os pontos-chave de entrada para os quantis de recursos.

Para recursos categóricos, o TensorFlow Lattice fornece calibração categórica (com tfl.layers.CategoricalCalibration ) com limites de saída semelhantes para alimentar uma treliça.

Conjuntos

O número de parâmetros de uma camada de treliça aumenta exponencialmente com o número de recursos de entrada, portanto, não escala bem para dimensões muito altas. Para superar essa limitação, o TensorFlow Lattice oferece conjuntos de treliças que combinam (em média) várias treliças minúsculas , o que permite que o modelo cresça linearmente no número de recursos.

A biblioteca fornece duas variações desses conjuntos:

  • Random Tiny Lattices (RTL): Cada submodelo usa um subconjunto aleatório de recursos (com substituição).

  • Crystals : O algoritmo Crystals primeiro treina um modelo de pré -ajuste que estima interações de recursos em pares. Em seguida, ele organiza o conjunto final de modo que os recursos com mais interações não lineares estejam nas mesmas redes.

Por que o TensorFlow Lattice?

Você pode encontrar uma breve introdução ao TensorFlow Lattice nesta postagem do TF Blog .

Interpretabilidade

Como os parâmetros de cada camada são a saída dessa camada, é fácil analisar, entender e depurar cada parte do modelo.

Modelos precisos e flexíveis

Usando treliças refinadas, você pode obter funções arbitrariamente complexas com uma única camada de treliça. O uso de várias camadas de calibradores e treliças geralmente funciona bem na prática e pode corresponder ou superar modelos DNN de tamanhos semelhantes.

Restrições de forma de senso comum

Os dados de treinamento do mundo real podem não representar suficientemente os dados de tempo de execução. Soluções flexíveis de ML, como DNNs ou florestas, geralmente agem de maneira inesperada e até descontrolada em partes do espaço de entrada não cobertas pelos dados de treinamento. Esse comportamento é especialmente problemático quando restrições de política ou justiça podem ser violadas.

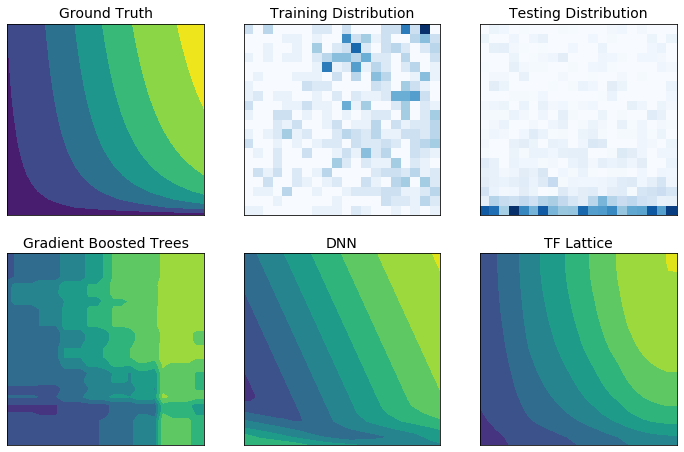
Embora as formas comuns de regularização possam resultar em extrapolação mais sensata, os regularizadores padrão não podem garantir um comportamento razoável do modelo em todo o espaço de entrada, especialmente com entradas de alta dimensão. Mudar para modelos mais simples com comportamento mais controlado e previsível pode ter um custo severo para a precisão do modelo.

O TF Lattice torna possível continuar usando modelos flexíveis, mas oferece várias opções para injetar conhecimento de domínio no processo de aprendizado por meio de restrições de forma semanticamente significativas ou orientadas por políticas:

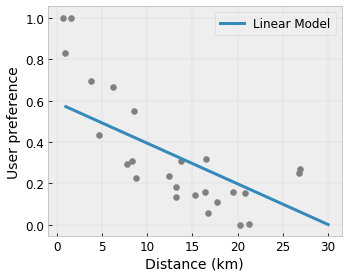
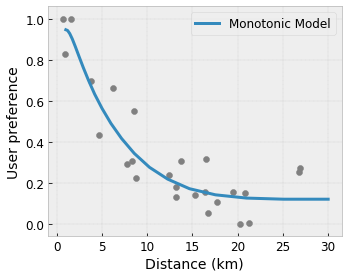
  • Monotonicidade : Você pode especificar que a saída só deve aumentar/diminuir em relação a uma entrada. Em nosso exemplo, você pode especificar que o aumento da distância até uma cafeteria deve apenas diminuir a preferência prevista do usuário.

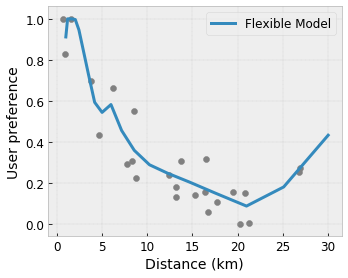
  • Convexity/Concavity : Você pode especificar que a forma da função pode ser convexa ou côncava. Misturado com monotonicidade, isso pode forçar a função a representar retornos decrescentes em relação a um determinado recurso.

  • Unimodalidade : Você pode especificar que a função deve ter um pico ou vale único. Isso permite representar funções que têm um ponto ideal em relação a um recurso.

  • Confiança em pares : essa restrição funciona em um par de recursos e sugere que um recurso de entrada reflita semanticamente a confiança em outro recurso. Por exemplo, um número maior de avaliações deixa você mais confiante na classificação média por estrelas de um restaurante. O modelo será mais sensível em relação à classificação por estrelas (ou seja, terá uma inclinação maior em relação à classificação) quando o número de avaliações for maior.

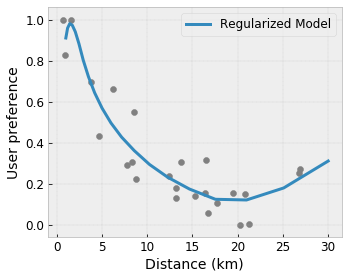
Flexibilidade Controlada com Regularizadores

Além das restrições de forma, a treliça do TensorFlow fornece vários regularizadores para controlar a flexibilidade e a suavidade da função para cada camada.

  • Regularizador Laplaciano : As saídas da rede/vértices/pontos-chave de calibração são regularizadas para os valores de seus respectivos vizinhos. Isso resulta em uma função mais plana .

  • Regularizador Hessiano : Isso penaliza a primeira derivada da camada de calibração PWL para tornar a função mais linear .

  • Wrinkle Regularizer : Isso penaliza a segunda derivada da camada de calibração PWL para evitar mudanças repentinas na curvatura. Isso torna a função mais suave.

  • Torsion Regularizer : As saídas da rede serão regularizadas para evitar torção entre as feições. Em outras palavras, o modelo será regularizado no sentido de independência entre as contribuições das características.

Misture e combine com outras camadas Keras

Você pode usar camadas TF Lattice em combinação com outras camadas Keras para construir modelos parcialmente restritos ou regularizados. Por exemplo, camadas de calibração de treliça ou PWL podem ser usadas na última camada de redes mais profundas que incluem embeddings ou outras camadas Keras.

Papéis

Tutoriais e documentos da API

Para arquiteturas de modelos comuns, você pode usar modelos pré- fabricados Keras ou estimadores pré-fabricados. Você também pode criar modelos personalizados usando camadas TF Lattice Keras ou misturar e combinar com outras camadas Keras. Confira os documentos completos da API para obter detalhes.