Krata TensorFlow (TFL)

TensorFlow Lattice to biblioteka implementująca elastyczne, kontrolowane i interpretowalne modele oparte na kratach. Biblioteka umożliwia wprowadzenie wiedzy dziedzinowej do procesu uczenia się poprzez ograniczenia kształtu oparte na zdrowym rozsądku lub zasadach. Odbywa się to za pomocą zbioru warstw Keras , które mogą spełniać ograniczenia, takie jak monotoniczność, wypukłość i zaufanie parami. Biblioteka udostępnia także łatwe w konfiguracji, gotowe modele .

Koncepcje

Ta sekcja stanowi uproszczoną wersję opisu w Monotonic Calibrated Interpolated Look-Up Tables , JMLR 2016.

Kraty

Krata to interpolowana tabela przeglądowa, która może przybliżać dowolne relacje wejście-wyjście w danych. Nakłada się na zwykłą siatkę na przestrzeń wejściową i uczy się wartości wyjściowych w wierzchołkach siatki. Dla punktu testowego \(x\), \(f(x)\) jest interpolowana liniowo z otaczających wartości sieci \(x\).

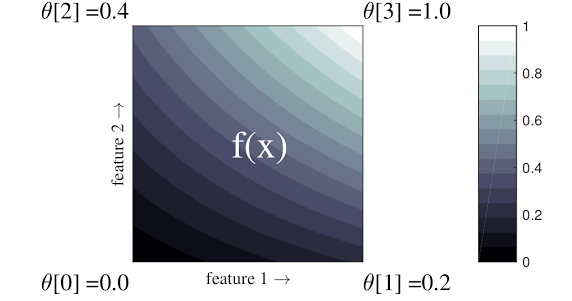
Powyższy prosty przykład to funkcja z 2 cechami wejściowymi i 4 parametrami:\(\theta=[0, 0.2, 0.4, 1]\), które są wartościami funkcji w rogach przestrzeni wejściowej; reszta funkcji jest interpolowana na podstawie tych parametrów.

Funkcja \(f(x)\) może uchwycić nieliniowe interakcje między obiektami. Parametry sieci można traktować jako wysokość słupów osadzonych w ziemi na regularnej siatce, a uzyskana funkcja przypomina tkaninę naciągniętą ciasno na cztery słupy.

Z \(D\) cechy i 2 wierzchołki wzdłuż każdego wymiaru, będzie miała regularna krata \(2^D\) parametry. Aby dopasować bardziej elastyczną funkcję, można określić drobnoziarnistą siatkę nad przestrzenią cech z większą liczbą wierzchołków wzdłuż każdego wymiaru. Funkcje regresji kratowej są ciągłe i odcinkowo nieskończenie różniczkowalne.

Kalibrowanie

Załóżmy, że powyższa przykładowa siatka reprezentuje wyuczone zadowolenie użytkownika z sugerowaną lokalną kawiarnią obliczoną przy użyciu funkcji:

  • cena kawy w przedziale od 0 do 20 dolarów
  • odległość od użytkownika, w zakresie od 0 do 30 kilometrów

Chcemy, aby nasz model uczył się szczęścia użytkownika dzięki sugestii lokalnej kawiarni. Modele TensorFlow Lattice mogą wykorzystywać odcinkowe funkcje liniowe (z tfl.layers.PWLCalibration ) do kalibracji i normalizacji cech wejściowych do zakresu akceptowanego przez sieć: od 0,0 do 1,0 w przykładowej sieci powyżej. Poniżej przedstawiono przykłady takich funkcji kalibracji z 10 punktami kluczowymi:

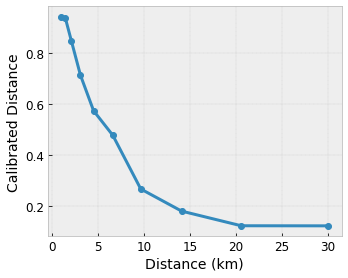
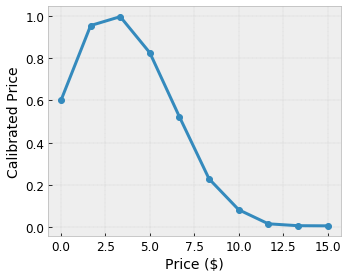
Często dobrym pomysłem jest użycie kwantyli cech jako wejściowych punktów kluczowych. Gotowe modele TensorFlow Lattice mogą automatycznie ustawiać wejściowe punkty kluczowe na kwantyle cech.

W przypadku cech jakościowych TensorFlow Lattice zapewnia kalibrację kategorialną (za pomocą tfl.layers.CategoricalCalibration ) z podobnymi ograniczeniami wyjściowymi w celu zasilania sieci.

Zespoły

Liczba parametrów warstwy siatki rośnie wykładniczo wraz z liczbą cech wejściowych, dlatego nie skaluje się dobrze do bardzo dużych wymiarów. Aby pokonać to ograniczenie, TensorFlow Lattice oferuje zespoły sieci, które łączą (średnio) kilka małych sieci, co umożliwia liniowy wzrost liczby cech modelu.

Biblioteka udostępnia dwie odmiany tych zespołów:

  • Losowe małe kraty (RTL): każdy podmodel wykorzystuje losowy podzbiór funkcji (z wymianą).

  • Kryształy : Algorytm Kryształy najpierw szkoli model wstępnego dopasowania , który szacuje interakcje cech parami. Następnie organizuje ostateczny zespół w taki sposób, że cechy z bardziej nieliniowymi interakcjami znajdują się w tych samych sieciach.

Dlaczego siatka TensorFlow?

Krótkie wprowadzenie do TensorFlow Lattice można znaleźć w tym poście na blogu TF .

Interpretowalność

Ponieważ parametry każdej warstwy są wynikami tej warstwy, łatwo jest analizować, rozumieć i debugować każdą część modelu.

Dokładne i elastyczne modele

Używając drobnoziarnistych siatek, można uzyskać dowolnie złożone funkcje za pomocą pojedynczej warstwy siatki. Stosowanie wielu warstw kalibratorów i siatek często sprawdza się w praktyce i może dorównywać lub przewyższać modele DNN o podobnych rozmiarach.

Zdroworozsądkowe ograniczenia kształtu

Dane szkoleniowe ze świata rzeczywistego mogą nie odzwierciedlać w wystarczającym stopniu danych wykonawczych. Elastyczne rozwiązania ML, takie jak DNN lub lasy, często działają nieoczekiwanie, a nawet dziko w częściach przestrzeni wejściowej nieobjętych danymi szkoleniowymi. Takie zachowanie jest szczególnie problematyczne, gdy mogą zostać naruszone zasady lub ograniczenia uczciwości.

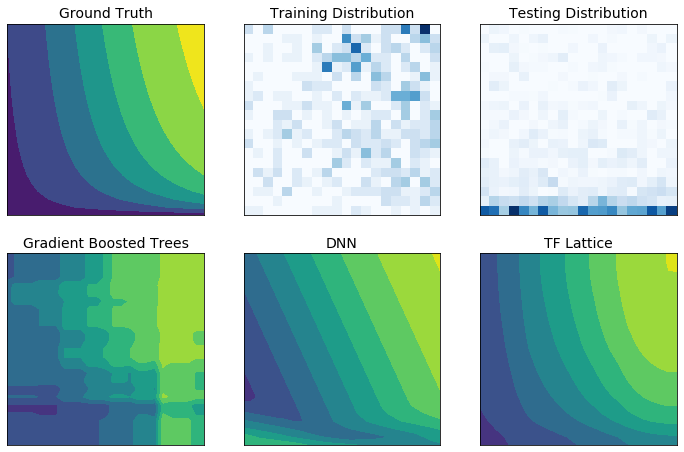
Chociaż typowe formy regularyzacji mogą skutkować bardziej rozsądną ekstrapolacją, standardowe regularyzatory nie mogą zagwarantować rozsądnego zachowania modelu w całej przestrzeni wejściowej, szczególnie w przypadku danych wejściowych o dużych wymiarach. Przejście na prostsze modele o bardziej kontrolowanym i przewidywalnym zachowaniu może wiązać się z poważnym kosztem dokładności modelu.

TF Lattice umożliwia dalsze korzystanie z elastycznych modeli, ale zapewnia kilka opcji wstrzyknięcia wiedzy dziedzinowej do procesu uczenia się poprzez ograniczenia kształtu mające znaczenie semantyczne, wynikające ze zdrowego rozsądku lub polityki:

  • Monotoniczność : Można określić, że sygnał wyjściowy powinien rosnąć/zmniejszać się tylko w stosunku do sygnału wejściowego. W naszym przykładzie możesz chcieć określić, że zwiększona odległość do kawiarni powinna jedynie zmniejszyć przewidywane preferencje użytkownika.

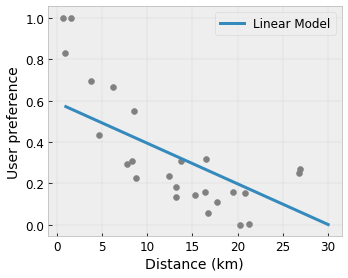
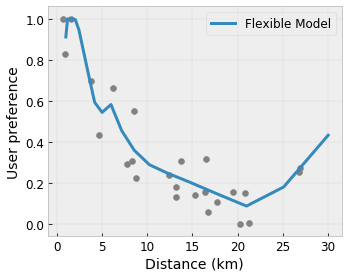
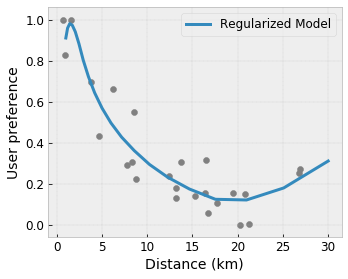
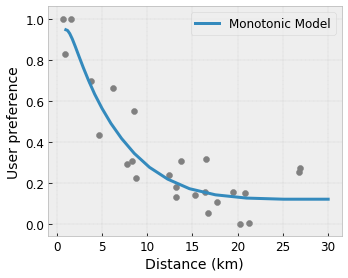
  • Wypukłość/wklęsłość : możesz określić, że kształt funkcji może być wypukły lub wklęsły. W połączeniu z monotonicznością może to zmusić funkcję do reprezentowania malejących zysków w odniesieniu do danej cechy.

  • Unimodalność : Można określić, że funkcja powinna mieć unikalny szczyt lub unikalną dolinę. Pozwala to reprezentować funkcje, które mają dobry punkt w odniesieniu do cechy.

  • Zaufanie parami : to ograniczenie działa na parę cech i sugeruje, że jedna cecha wejściowa semantycznie odzwierciedla zaufanie do innej cechy. Na przykład większa liczba recenzji zwiększa pewność średniej oceny restauracji w gwiazdkach. Model będzie bardziej czuły w odniesieniu do oceny w postaci gwiazdek (tzn. będzie miał większe nachylenie w stosunku do oceny), gdy liczba recenzji będzie większa.

Kontrolowana elastyczność dzięki regularizerom

Oprócz ograniczeń kształtu siatka TensorFlow zapewnia szereg regulatorów kontrolujących elastyczność i gładkość funkcji dla każdej warstwy.

  • Regularyzator Laplaciana : Wyniki sieci/wierzchołków kalibracyjnych/punktów kluczowych są regulowane w kierunku wartości ich odpowiednich sąsiadów. Powoduje to bardziej płaską funkcję.

  • Regularizator Hesja : Penalizuje pierwszą pochodną warstwy kalibracyjnej PWL, czyniąc funkcję bardziej liniową .

  • Urządzenie do korygowania zmarszczek : karze drugą pochodną warstwy kalibracyjnej PWL, aby uniknąć nagłych zmian krzywizny. Dzięki temu funkcja jest płynniejsza.

  • Stabilizator skrętu : Wyjścia siatki zostaną uregulowane w celu zapobiegania skręcaniu się elementów. Innymi słowy, model zostanie uregulowany w kierunku niezależności wkładów cech.

Mieszaj i łącz z innymi warstwami Keras

Warstwy TF Lattice można używać w połączeniu z innymi warstwami Keras, aby konstruować modele częściowo ograniczone lub uregulowane. Na przykład warstwy kalibracyjne kratowe lub PWL można zastosować w ostatniej warstwie głębszych sieci zawierających osady lub inne warstwy Keras.

Dokumenty tożsamości

Poradniki i dokumentacja API

W przypadku typowych architektur modeli można używać gotowych modeli Keras . Można także tworzyć niestandardowe modele przy użyciu warstw TF Lattice Keras lub mieszać i dopasowywać je do innych warstw Keras. Aby uzyskać szczegółowe informacje, zapoznaj się z pełną dokumentacją API .

,

TensorFlow Lattice to biblioteka implementująca elastyczne, kontrolowane i interpretowalne modele oparte na kratach. Biblioteka umożliwia wprowadzenie wiedzy dziedzinowej do procesu uczenia się poprzez ograniczenia kształtu oparte na zdrowym rozsądku lub zasadach. Odbywa się to za pomocą zbioru warstw Keras , które mogą spełniać ograniczenia, takie jak monotoniczność, wypukłość i zaufanie parami. Biblioteka udostępnia także łatwe w konfiguracji, gotowe modele .

Koncepcje

Ta sekcja stanowi uproszczoną wersję opisu w Monotonic Calibrated Interpolated Look-Up Tables , JMLR 2016.

Kraty

Krata to interpolowana tabela przeglądowa, która może przybliżać dowolne relacje wejście-wyjście w danych. Nakłada zwykłą siatkę na przestrzeń wejściową i uczy się wartości wyjściowych w wierzchołkach siatki. Dla punktu testowego \(x\), \(f(x)\) jest interpolowana liniowo z otaczających wartości sieci \(x\).

Powyższy prosty przykład to funkcja z 2 cechami wejściowymi i 4 parametrami:\(\theta=[0, 0.2, 0.4, 1]\), które są wartościami funkcji w rogach przestrzeni wejściowej; reszta funkcji jest interpolowana na podstawie tych parametrów.

Funkcja \(f(x)\) może uchwycić nieliniowe interakcje między obiektami. Parametry sieci można traktować jako wysokość słupów osadzonych w ziemi na regularnej siatce, a uzyskana funkcja przypomina tkaninę naciągniętą ciasno na cztery słupy.

Z \(D\) cechy i 2 wierzchołki wzdłuż każdego wymiaru, będzie miała regularna krata \(2^D\) parametry. Aby dopasować bardziej elastyczną funkcję, można określić drobnoziarnistą siatkę nad przestrzenią cech z większą liczbą wierzchołków wzdłuż każdego wymiaru. Funkcje regresji kratowej są ciągłe i odcinkowo nieskończenie różniczkowalne.

Kalibrowanie

Załóżmy, że powyższa przykładowa siatka reprezentuje wyuczone zadowolenie użytkownika z sugerowaną lokalną kawiarnią obliczoną przy użyciu funkcji:

  • cena kawy w przedziale od 0 do 20 dolarów
  • odległość od użytkownika, w zakresie od 0 do 30 kilometrów

Chcemy, aby nasz model uczył się szczęścia użytkownika dzięki sugestii lokalnej kawiarni. Modele TensorFlow Lattice mogą wykorzystywać odcinkowe funkcje liniowe (z tfl.layers.PWLCalibration ) do kalibracji i normalizacji cech wejściowych do zakresu akceptowanego przez sieć: od 0,0 do 1,0 w przykładowej sieci powyżej. Poniżej przedstawiono przykłady takich funkcji kalibracji z 10 punktami kluczowymi:

Często dobrym pomysłem jest użycie kwantyli cech jako wejściowych punktów kluczowych. Gotowe modele TensorFlow Lattice mogą automatycznie ustawiać wejściowe punkty kluczowe na kwantyle cech.

W przypadku cech jakościowych TensorFlow Lattice zapewnia kalibrację kategorialną (za pomocą tfl.layers.CategoricalCalibration ) z podobnymi ograniczeniami wyjściowymi w celu zasilania sieci.

Zespoły

Liczba parametrów warstwy siatki rośnie wykładniczo wraz z liczbą cech wejściowych, dlatego nie skaluje się dobrze do bardzo dużych wymiarów. Aby pokonać to ograniczenie, TensorFlow Lattice oferuje zespoły sieci, które łączą (średnio) kilka małych sieci, co umożliwia liniowy wzrost liczby cech modelu.

Biblioteka udostępnia dwie odmiany tych zespołów:

  • Losowe małe kraty (RTL): każdy podmodel wykorzystuje losowy podzbiór funkcji (z wymianą).

  • Kryształy : Algorytm Kryształy najpierw szkoli model wstępnego dopasowania , który szacuje interakcje cech parami. Następnie organizuje ostateczny zespół w taki sposób, że cechy z bardziej nieliniowymi interakcjami znajdują się w tych samych sieciach.

Dlaczego siatka TensorFlow?

Krótkie wprowadzenie do TensorFlow Lattice można znaleźć w tym poście na blogu TF .

Interpretowalność

Ponieważ parametry każdej warstwy są wynikami tej warstwy, łatwo jest analizować, rozumieć i debugować każdą część modelu.

Dokładne i elastyczne modele

Używając drobnoziarnistych siatek, można uzyskać dowolnie złożone funkcje za pomocą pojedynczej warstwy siatki. Stosowanie wielu warstw kalibratorów i siatek często sprawdza się w praktyce i może dorównywać lub przewyższać modele DNN o podobnych rozmiarach.

Zdroworozsądkowe ograniczenia kształtu

Dane szkoleniowe ze świata rzeczywistego mogą nie odzwierciedlać w wystarczającym stopniu danych wykonawczych. Elastyczne rozwiązania ML, takie jak DNN lub lasy, często działają nieoczekiwanie, a nawet dziko w częściach przestrzeni wejściowej nieobjętych danymi szkoleniowymi. Takie zachowanie jest szczególnie problematyczne, gdy mogą zostać naruszone zasady lub ograniczenia uczciwości.

Chociaż typowe formy regularyzacji mogą skutkować bardziej rozsądną ekstrapolacją, standardowe regularyzatory nie mogą zagwarantować rozsądnego zachowania modelu w całej przestrzeni wejściowej, szczególnie w przypadku danych wejściowych o dużych wymiarach. Przejście na prostsze modele o bardziej kontrolowanym i przewidywalnym zachowaniu może wiązać się z poważnym kosztem dokładności modelu.

TF Lattice umożliwia dalsze korzystanie z elastycznych modeli, ale zapewnia kilka opcji wstrzyknięcia wiedzy dziedzinowej do procesu uczenia się poprzez ograniczenia kształtu mające znaczenie semantyczne, wynikające ze zdrowego rozsądku lub polityki:

  • Monotoniczność : Można określić, że sygnał wyjściowy powinien się zwiększać/zmniejszać jedynie w stosunku do sygnału wejściowego. W naszym przykładzie możesz chcieć określić, że zwiększona odległość do kawiarni powinna jedynie zmniejszyć przewidywane preferencje użytkownika.

  • Wypukłość/wklęsłość : możesz określić, że kształt funkcji może być wypukły lub wklęsły. W połączeniu z monotonicznością może to zmusić funkcję do reprezentowania malejących zysków w odniesieniu do danej cechy.

  • Unimodalność : Można określić, że funkcja powinna mieć unikalny szczyt lub unikalną dolinę. Pozwala to reprezentować funkcje, które mają dobry punkt w odniesieniu do cechy.

  • Zaufanie parami : to ograniczenie działa na parę cech i sugeruje, że jedna cecha wejściowa semantycznie odzwierciedla zaufanie do innej cechy. Na przykład większa liczba recenzji zwiększa pewność średniej oceny restauracji w gwiazdkach. Model będzie bardziej czuły w odniesieniu do oceny w postaci gwiazdek (tj. będzie miał większe nachylenie w stosunku do oceny), gdy liczba recenzji będzie większa.

Kontrolowana elastyczność dzięki regularizerom

Oprócz ograniczeń kształtu siatka TensorFlow zapewnia szereg regulatorów kontrolujących elastyczność i gładkość funkcji dla każdej warstwy.

  • Regularyzator Laplaciana : Wyniki sieci/wierzchołków kalibracyjnych/punktów kluczowych są regulowane w kierunku wartości ich odpowiednich sąsiadów. Powoduje to bardziej płaską funkcję.

  • Regularizator Hesja : Penalizuje pierwszą pochodną warstwy kalibracyjnej PWL, czyniąc funkcję bardziej liniową .

  • Urządzenie do korygowania zmarszczek : karze drugą pochodną warstwy kalibracyjnej PWL, aby uniknąć nagłych zmian krzywizny. Dzięki temu funkcja jest płynniejsza.

  • Stabilizator skrętu : Wyjścia siatki zostaną uregulowane w celu zapobiegania skręcaniu się elementów. Innymi słowy, model zostanie uregulowany w kierunku niezależności wkładów cech.

Mieszaj i łącz z innymi warstwami Keras

Warstwy TF Lattice można używać w połączeniu z innymi warstwami Keras, aby konstruować modele częściowo ograniczone lub uregulowane. Na przykład warstwy kalibracyjne kratowe lub PWL można zastosować w ostatniej warstwie głębszych sieci zawierających osady lub inne warstwy Keras.

Dokumenty tożsamości

Poradniki i dokumentacja API

W przypadku typowych architektur modeli można używać gotowych modeli Keras . Można także tworzyć niestandardowe modele przy użyciu warstw TF Lattice Keras lub mieszać i dopasowywać je do innych warstw Keras. Aby uzyskać szczegółowe informacje, zapoznaj się z pełną dokumentacją API .