TensorFlow Lattice(TFL)

TensorFlow Lattice는 유연하고 제어되며 해석 가능한 격자 기반 모델을 구현하는 라이브러리입니다. 라이브러리를 사용하면 상식적이거나 정책 중심의 형상 제약 조건을 통해 학습 프로세스에 도메인 지식을 주입할 수 있습니다. 이는 단조, 볼록 및 쌍별 신뢰와 같은 제약 조건을 충족할 수 있는 Keras 레이어 모음을 사용하여 수행됩니다. 라이브러리는 또한 쉽게 설정할 수 있는 준비된 estimator를 제공합니다.

개념

이 섹션에서는 Monotonic Calibrated Interpolated Look-Up Tables , JMLR 2016의 설명을 단순화한 버전이 나옵니다.

격자

격자는 데이터의 임의의 입력-출력 관계를 근사화할 수 있는 보간된 조회 테이블입니다. 입력 공간에 일반 그리드를 겹치고 그리드의 꼭짓점에서 출력값을 학습합니다. 테스트 포인트 \(x\)의 경우 \(f(x)\)는 \(x\)를 둘러싼 격자 값에서 선형으로 보간됩니다.

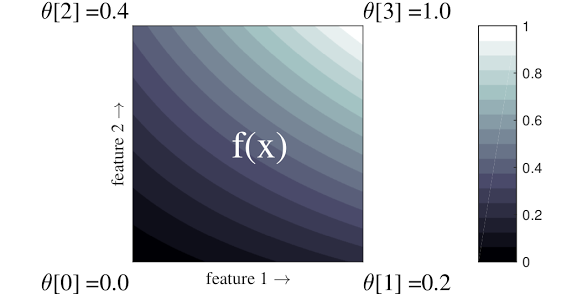
위의 간단한 예는 2개의 입력 특성과 4개의 매개변수가 있는 함수입니다. \(\theta=[0, 0.2, 0.4, 1]\), 즉, 입력 공간의 모서리에 있는 함수의 값입니다. 나머지 함수는 이러한 매개변수에서 보간됩니다.

\(f(x)\) 함수는 특성 간의 비선형 상호 작용을 캡처할 수 있습니다. 격자 매개변수는 일반 격자의 지면에 설정된 극의 높이로 생각할 수 있으며 결과 함수는 네 개의 극에 대해 천을 단단히 잡아당기는 것과 같습니다.

\(D\) 특성과 각 차원을 따라 2개의 꼭짓점이 있는 일반 격자에는 \(2^D\) 매개변수가 있습니다. 보다 유연한 함수에 맞추기 위해 각 차원을 따라 더 많은 꼭짓점이 있는 특성 공간에 더 미세한 격자를 지정할 수 있습니다. 격자 회귀 함수는 연속적이고 부분적으로 무한 미분할 수 있습니다.

보정

앞의 샘플 격자가 특성을 사용하여 계산된 추천 지역 커피숍을 통해 학습된 사용자의 행복을 나타낸다고 가정해 보겠습니다.

  • 커피 가격(0~20 달러)
  • 사용자까지의 거리(범위: 0~30km)

모델이 지역 커피숍 추천으로 사용자의 행복에 대해 학습합니다. TensorFlow Lattice 모델은 구간 선형 함수( tfl.layers.PWLCalibration)를 사용하여 위의 예제 격자에서 0.0에서 1.0까지 격자가 허용하는 범위로 입력 특성을 보정하고 정규화할 수 있습니다. 다음은 10개의 키포인트가 있는 보정 함수의 예를 보여줍니다.

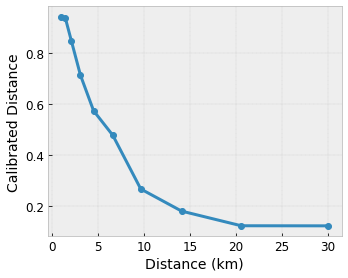
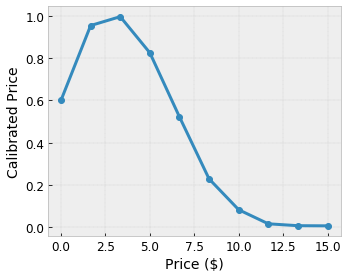
특성의 분위수를 입력 키포인트로 사용하는 것이 좋습니다. TensorFlow Lattice 준비된 estimator는 입력 키포인트를 특성 분위수로 자동 설정할 수 있습니다.

범주형 특성의 경우 TensorFlow Lattice는 격자에 공급할 유사한 출력 경계를 사용하여 범주형 보정(tfl.layers.CategoricalCalibration)을 제공합니다.

앙상블

격자 레이어의 매개변수 수는 입력 특성의 수에 따라 기하급수적으로 증가하기 때문에 매우 높은 차원으로 조정되지는 않습니다. 이러한 한계를 극복하기 위해 TensorFlow Lattice는 여러 개의 작은 격자를 결합(평균)하는 격자 앙상블을 제공하여 모델이 특성 수에서 선형으로 성장할 수 있도록 합니다.

라이브러리는 이러한 앙상블의 두 가지 변형을 제공합니다.

  • Random Tiny Lattices(RTL): 각 하위 모델은 특성의 무작위 하위 집합(대체 포함)을 사용합니다.

  • Crystasl: Crystal 알고리즘은 먼저 쌍별 특성 상호 작용을 예측하는 사전 적합 모델을 훈련합니다. 그런 다음 비선형 상호 작용이 더 많은 특성이 동일한 격자에 있도록 최종 앙상블을 정렬합니다.

왜 TensorFlow Lattice인가?

TF 블로그 게시물에서 TensorFlow Lattice에 대한 간략한 소개를 확인할 수 있습니다.

해석 가능성

각 레이어의 매개변수는 해당 레이어의 출력이므로 모델의 각 부분을 분석, 이해 및 디버그하기 쉽습니다.

정확하고 유연한 모델

세분화된 격자를 사용하면 단일 격자 레이어로 임의의 복잡한 함수를 얻을 수 있습니다. 여러 레이어의 calibrator와 격자를 사용하면 실제로 잘 동작하며 비슷한 크기의 DNN 모델과 일치하거나 성능을 능가할 수 있습니다.

상식적인 형상 제약 조건

실제 훈련 데이터는 런타임 데이터를 충분히 나타내지 못할 수 있습니다. DNN 또는 포리스트와 같은 유연한 ML 솔루션은 훈련 데이터가 다루지 않는 입력 공간의 일부에서 예기치 않게, 격렬하게 동작하는 경우가 많습니다. 이 동작은 정책 또는 공정성 제약 조건이 위반될 수 있는 경우 특히 문제가 됩니다.

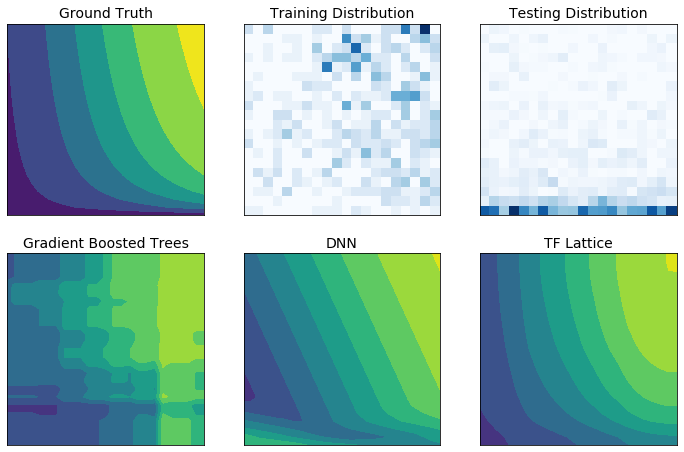
일반적인 형태의 정규화가 더 합리적인 외삽을 가져올 수 있지만, 표준 정규화는 특히 고차원 입력에서 전체 입력 공간에 걸쳐 합리적인 모델 동작을 보장할 수 없습니다. 보다 제어되고 예측 가능한 동작을 가진 더 단순한 모델로 전환하면 모델 정확성에 심각한 비용이 발생할 수 있습니다.

TF Lattice를 사용하면 유연한 모델을 계속 사용할 수 있지만, 의미상 의미 있는 상식 또는 정책 기반 형상 제약 조건을 통해 학습 프로세스에 도메인 지식을 주입할 수 있는 몇 가지 옵션을 제공합니다.

  • 단조: 입력에 대해 출력이 증가/감소하도록 지정할 수 있습니다. 이 예에서는 커피숍까지의 거리가 늘어날 경우 예상 사용자 선호도만 감소하도록 지정할 수 있습니다.

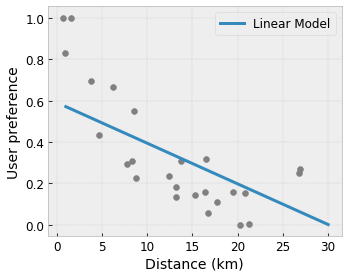
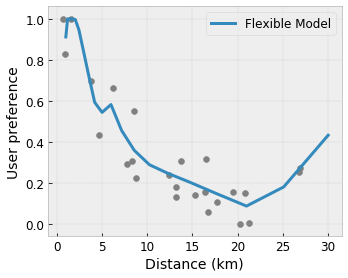
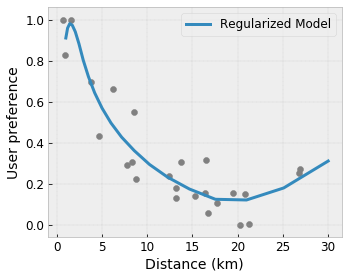
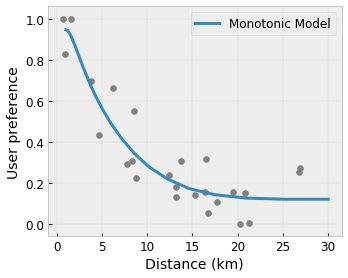
  • 볼록/오목: 함수 형상을 볼록하거나 오목하도록 지정할 수 있습니다. 단조와 혼합되면 함수가 주어진 특성에 대해 감소하는 수익을 나타내도록 강제할 수 있습니다.

  • 단봉: 함수가 고유한 피크 또는 고유한 밸리를 갖도록 지정할 수 있습니다. 이를 통해 특성과 관련하여 최적의 지점이 있는 함수를 나타낼 수 있습니다.

  • 쌍별 신뢰: 이 제약 조건은 한 쌍의 특성에서 동작하며 하나의 입력 특성이 다른 특성에 대한 신뢰를 의미상으로 반영한다는 점을 나타냅니다. 예를 들어 리뷰 수가 많을수록 레스토랑의 평균 별점에 대해 더 강하게 확신할 수 있습니다. 리뷰 수가 많을 때 모델은 별 등급에 대해 더 민감합니다(즉, 등급에 대해 더 큰 기울기를 가짐).

Regularizer로 유연성 제어

형상 제약 조건외에도 TensorFlow 격자는 각 레이어에 대한 특성의 유연성과 매끄러움을 제어하도록 여러 Regularizer를 제공합니다.

  • Laplacian Regularizer: 격자/보정 꼭지점/키포인트의 출력이 해당 인접 항목의 값으로 정규화됩니다. 이로 인해 더 평평한 함수가 생성됩니다.

  • Hessian Regularizer: 함수를 보다 선형적으로 만들기 위해 PWL 보정 레이어의 1차 도함수에 페널티를 줍니다.

  • Wrinkle Regularizer: 곡률의 갑작스러운 변화를 방지하기 위해 PWL 보정 레이어의 2차 도함수에 페널티를 줍니다. 이로써 특성을 더 매끄럽게 만듭니다.

  • Torsion Regularizer: 격자의 출력이 특성 간의 비틀림을 방지하기 위해 정규화됩니다. 즉, 모델은 특성의 기여도 사이의 독립성을 향해 정규화됩니다.

다른 Keras 레이어와 혼합하기 및 일치하기

TF Lattice 레이어를 다른 Keras 레이어와 함께 사용하여 부분적으로 제한되거나 정규화된 모델을 구성할 수 있습니다. 예를 들어, 격자 또는 PWL 보정 레이어는 임베딩 또는 기타 Keras 레이어를 포함하는 심층 네트워크의 마지막 레이어에서 사용할 수 있습니다.

논문

튜토리얼 및 API 설명서

일반적인 모델 아키텍처의 경우 Keras 사전 제작 모델 또는 준비된 Estimators를 사용할 수 있습니다. TF Lattice Keras 레이어를 사용하여 사용자 정의 모델을 생성하거나 다른 Keras 레이어와 혼합 및 일치시킬 수도 있습니다. 자세한 내용은 전체 API 설명서를 확인하세요.