TensorFlow Lattice は、柔軟性があり制御と解釈が可能な格子ベースのモデルを実装するライブラリです。このライブラリを使用すると、常識やポリシー重視の形状制約を通して、学習プロセスにドメインの知識を注入することができます。これは単調性、凸性、ペアワイズ信頼などの制約を満たすことができる Keras レイヤーのコレクションを使用して行います。また、このライブラリはセットアップが容易な Canned Estimator も提供しています。
コンセプト
本セクションは、単調性較正補間ルックアップテーブル、JMLR (2016) の説明を簡略化したものです。
格子
格子は、データ内の任意の入出力関係を近似することができる補間ルックアップテーブルです。構造格子を入力空間にオーバーラップさせ、グリッドの頂点で出力の値を学習します。テストポイントが \(x\) の場合、\(f(x)\) は \(x\) を囲む格子の値から線形補間されます。
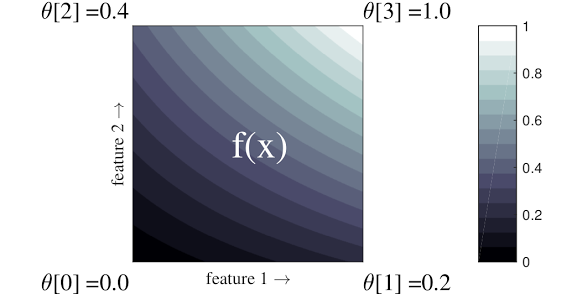
上記の簡単な例は 2 つの入力特徴量と 4 つのパラメータを持つ関数です。\(\theta=[0, 0.2, 0.4, 1]\) は入力空間の隅にある関数の値です。関数の残りの部分は、これらのパラメータから補間されます。
関数 \(f(x)\) は、特徴量間の非線形相互作用をキャプチャすることができます。格子パラメータは構造格子の底に設置した軸の高さと考えることができ、結果の関数は 4 つの軸に布をきつく張りつめたようなものです。
\(D\) の特徴量と各次元に沿った 2 つの頂点を持つ規則的格子には、\(2^D\) パラメータがあります。より柔軟に関数を適合させるためには、各次元に沿ってより多い頂点を持つ特徴量空間上で、細かい格子を指定します。格子回帰関数は連続的であり、区分的に無限微分が可能です。
較正
前述のサンプル格子が、特徴量を使用して計算し学習された、特定の地元のコーヒーショップ利用者の満足度を表しているとします。
- コーヒーの価格、0 ~ 20 ドルの範囲
- 利用者からの距離、0 ~ 30 km の範囲
地元のコーヒーショップの提案で、モデルが利用者の満足度を学習できるようにしたいと考えています。TensorFlow Lattice モデルは区分的線形関数を(tfl.layer.PWLCalibrationと共に)使用して、格子が受け入れられる範囲の入力特徴量に較正し、正規化することができます。上記の例の格子の範囲は 0.0 ~ 1.0 です。以下に 10 個のキーポイントを持つ較正関数の例を示します。


入力キーポイントとして特徴量の分位数の使用をお勧めします。TensorFlow Lattice Canned Estimator は、入力キーポイントを特徴量分位数に自動設定することができます。
分類別特徴量については、TensorFlow Lattice が分類較正を(tfl.layer.CategoricalCalibrationを使用して)提供し、同様の出力境界を格子にフィードします。
アンサンブル
格子レイヤーのパラメータ数は入力特徴量の数に応じて指数関数的に増加するため、非常に高い次元にはうまくスケーリングできません。この制限を克服するために、TensorFlow Lattice は複数の小さな格子を(平均的に)結合する、格子のアンサンブルを提供します。これにより、モデルが特徴量の数で線形に成長できるようになります。
ライブラリには、これらのアンサンブルの 2 つのバリエーションが用意されています。
Random Tiny Lattices (RTL) : 各サブモデルは、特徴量のランダムなサブセットを(置き換えで)使用します。
Crystals : Crystal アルゴリズムは、まず、ペアでのの特徴量の相互作用を推定する事前適合モデルをトレーニングします。次に、同じ格子内により多くの非線形相互作用を持つ特徴量が存在するように、最終的なアンサンブルを配置します。
TensorFlow Lattice を選ぶ理由
TensorFlow Lattice の簡単な紹介は、この TF ブログ記事に書かれています。
解釈可能性
各レイヤーのパラメータはそのレイヤーの出力なので、モデルの各部分の解析、理解、デバッグが容易にできます。
正確で柔軟性のあるモデル
細かい格子を使用すると、1 つの格子レイヤーで任意に複雑な関数を取得することができます。キャリブレータと格子のマルチレイヤーを使用すると、実践では多くの場合でうまく機能し、同程度の大きさの DNN モデルと一致したり、それよりも優れたパフォーマンスを発揮したりします。
常識的な形状制約
実世界のトレーニングデータは、実行時のデータを十分に表現できない場合があります。DNN やフォレストのような柔軟性のある ML ソリューションは、トレーニングデータでカバーされていない入力空間の部分で、予期しない振る舞いや異なる振る舞いをすることもよくあります。特にこのような振る舞いがポリシーや公正の制約に違反する場合は問題となります。

一般的な正則化の形式ではより妥当な外挿結果が得られますが、標準的な正則化器は、特に高次元の入力の場合、入力空間全体にわたってモデルが合理的にを動作するという保証ができません。より制御され予測可能な動作をする単純なモデルに切り替えると、モデルの精度が大幅に低下する可能性があります。
TensorFlow Lattice では柔軟性のあるモデルを使い続けることが可能になりましたが、セマンティック的に意味のある常識またはポリシー重視の形状制約でドメインの知識を学習プロセスに注入するいくつかのオプションを提供しています。
- 単調性制約: 出力が入力のみに対して増減するように指定できます。この例では、コーヒーショップまでの距離が長くなると、予想されるユーザーの嗜好性のみが減少するように指定することができす。




凹凸性制約: 関数の形状を凸状または凹状に指定できます。単調性と混合すると、特定の特徴量に関して関数に強制的に減少リターンを表現させることができます。
単峰性制約: 関数が固有の山または固有の谷を持つように指定できます。これにより、任意の特徴量に関してスイートスポットを持つ関数を表現することができます。
ペアワイズ信頼制約: これは一対の特徴量に効果がある制約で、1 つの入力特徴量がもう 1 つの特徴量に対する信頼を意味的に反映することを示唆しています。例えば、レビューの数が多いほど、レストランの平均的な星評価への自信が深まります。レビューの数が増えると、モデルは星評価に関してより敏感に(つまり評価に関して傾きが大きく)なります。
正則化器を使用した柔軟性の制御
形状制約に加えて、TensorFlow Lattice には各レイヤーの関数の柔軟性と滑らかさを制御する、多数の正則化器が用意されています。
ラプラシアン正則化器: 格子、較正頂点、キーポイントの出力を、それぞれの近傍値に向かって正則化します。これにより、フラッター関数が得られます。
ヘッセ正則化器: PWL 較正レイヤーの 1 次導関数にペナルティを課して、関数をさらに線形にします。
リンクル正則化器: PWL 較正レイヤーの 2 次導関数にペナルティを課して、曲率の急激な変化を防ぎます。これにより、関数がより滑らかになります。
ねじれ正則化器: 特徴量間のねじれを防ぐため格子の出力を正則化します。言い換えると、特徴量の寄与間の独立性に向かってモデルを正則化します。
他の Keras レイヤーと組み合わせる
TF Lattice レイヤーを他の Keras レイヤーと組み合わせて使用して、部分的制約モデルや正則化モデルを構築することができます。例えば格子レイヤーや PWL 較正レイヤーは、Embedding レイヤーや他の Keras レイヤーを含む、さらに深いネットワークの最後のレイヤーで使用が可能です。
論文
- 単調性形状制約による義務論的倫理学、Serena Wang、Maya Gupta、International Conference on Artificial Intelligence and Statistics (AISTATS)、2020
- 集合関数の形状制約、Andrew Cotter、Maya Gupta、H. Jiang、Erez Louidor、Jim Muller、Taman Narayan、Serena Wang、Tao Zhu、International Conference on Machine Learning (ICML)、2019
- 解釈可能性と正則化のための収穫逓減形状制約、Maya Gupta、Dara Bahri、Andrew Cotter、Kevin Canini、Advances in Neural Information Processing Systems (NeurIPS)、2018
- 深層格子ネットワークと部分単調関数、Seungil You、Kevin Canini、David Ding、Jan Pfeifer、Maya R. Gupta、Advances in Neural Information Processing Systems (NeurIPS)、2017
- 格子の集合体による高速かつ柔軟性のある単調関数、Mahdi Milani Fard、Kevin Canini、Andrew Cotter、Jan Pfeifer、Maya Gupta、Advances in Neural Information Processing Systems (NeurIPS)、2016
- 単調性較正補間ルックアップテーブル、Maya Gupta、Andrew Cotter、Jan Pfeifer、Konstantin Voevodski、Kevin Canini、Alexander Mangylov、Wojciech Moczydlowski、Alexander van Esbroeck、Journal of Machine Learning Research (JMLR)、2016
- 効率的な関数評価のための最適化回帰法、Eric Garcia、Raman Arora、Maya R. Gupta、IEEE Transactions on Image Processing、2012
- 格子回帰法、Eric Garcia、Maya Gupta、Advances in Neural Information Processing Systems (NeurIPS)、2009
チュートリアルと API ドキュメント
一般的なモデルアーキテクチャでは、既製のKeras モデルや Canned Estimator を使用することができます。また、TF Lattice Keras レイヤーを使ったカスタムモデルの作成や、他の Keras レイヤーと組み合わせた使用も可能です。詳細については完全な API ドキュメントをご覧ください。
