TensorFlow Lattice es una biblioteca que implementa modelos basados en celosías flexibles, controlados e interpretables. La biblioteca le permite inyectar conocimiento del dominio en el proceso de aprendizaje a través de restricciones de forma impulsadas por políticas o de sentido común. Esto se hace utilizando una colección de capas de Keras que pueden satisfacer restricciones como monotonicidad, convexidad y confianza por pares. La biblioteca también proporciona modelos prefabricados fáciles de configurar.
Conceptos
Esta sección es una versión simplificada de la descripción en Tablas de búsqueda interpoladas calibradas monotónicas , JMLR 2016.
Celosías
Una celosía es una tabla de búsqueda interpolada que puede aproximarse a relaciones arbitrarias de entrada-salida en sus datos. Superpone una cuadrícula regular en su espacio de entrada y aprende valores para la salida en los vértices de la cuadrícula. Para un punto de prueba \(x\), \(f(x)\) se interpola linealmente a partir de los valores de red que rodean \(x\).
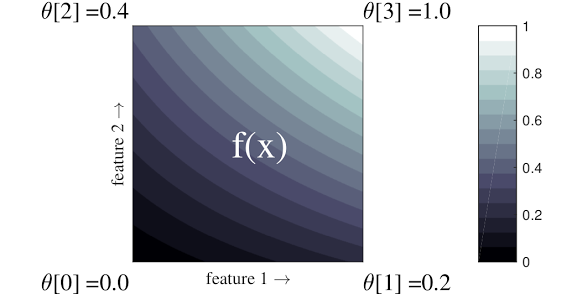
El ejemplo simple anterior es una función con 2 características de entrada y 4 parámetros:\(\theta=[0, 0.2, 0.4, 1]\), que son los valores de la función en las esquinas del espacio de entrada; el resto de la función se interpola a partir de estos parámetros.
la funcion \(f(x)\) Puede capturar interacciones no lineales entre características. Puede pensar en los parámetros de la red como la altura de los postes colocados en el suelo en una cuadrícula regular, y la función resultante es como una tela apretada contra los cuatro postes.
Con \(D\) características y 2 vértices a lo largo de cada dimensión, una red regular tendrá \(2^D\) parámetros. Para ajustar una función más flexible, puede especificar una red más fina sobre el espacio de características con más vértices a lo largo de cada dimensión. Las funciones de regresión reticular son continuas e infinitamente diferenciables por partes.
Calibración
Digamos que el ejemplo de celosía anterior representa la felicidad de un usuario aprendido con una cafetería local sugerida calculada usando características:
- Precio del café, en el rango de 0 a 20 dólares.
- distancia al usuario, en el rango de 0 a 30 kilómetros
Queremos que nuestro modelo aprenda sobre la felicidad del usuario con una sugerencia de cafetería local. Los modelos de TensorFlow Lattice pueden usar funciones lineales por partes (con tfl.layers.PWLCalibration ) para calibrar y normalizar las características de entrada al rango aceptado por la red: 0,0 a 1,0 en la red de ejemplo anterior. A continuación se muestran ejemplos de funciones de calibraciones con 10 puntos clave:
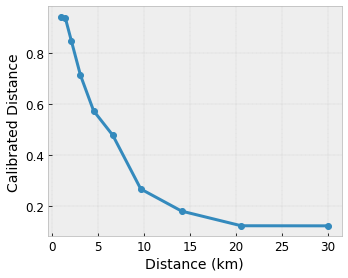
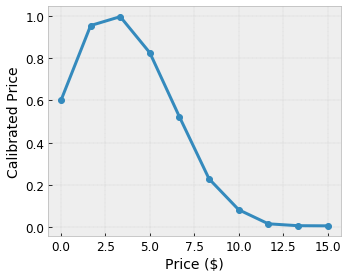
A menudo es una buena idea utilizar los cuantiles de las características como puntos clave de entrada. Los modelos prediseñados de TensorFlow Lattice pueden establecer automáticamente los puntos clave de entrada en los cuantiles de características.
Para funciones categóricas, TensorFlow Lattice proporciona calibración categórica (con tfl.layers.CategoricalCalibration ) con límites de salida similares para alimentar una red.
conjuntos
La cantidad de parámetros de una capa reticular aumenta exponencialmente con la cantidad de características de entrada, por lo que no se escala bien a dimensiones muy altas. Para superar esta limitación, TensorFlow Lattice ofrece conjuntos de celosías que combinan (en promedio) varias celosías pequeñas , lo que permite que el modelo crezca linealmente en el número de características.
La biblioteca ofrece dos variaciones de estos conjuntos:
Random Tiny Lattices (RTL): cada submodelo utiliza un subconjunto aleatorio de características (con reemplazo).
Crystals : el algoritmo Crystals primero entrena un modelo de preajuste que estima las interacciones de características por pares. Luego organiza el conjunto final de manera que las entidades con más interacciones no lineales estén en las mismas redes.
¿Por qué TensorFlow Lattice?
Puede encontrar una breve introducción a TensorFlow Lattice en esta publicación del blog de TF .
Interpretabilidad
Dado que los parámetros de cada capa son la salida de esa capa, es fácil analizar, comprender y depurar cada parte del modelo.
Modelos precisos y flexibles
Usando celosías de grano fino, puede obtener funciones arbitrariamente complejas con una sola capa de celosía. El uso de múltiples capas de calibradores y redes a menudo funciona bien en la práctica y puede igualar o superar a los modelos DNN de tamaños similares.
Restricciones de forma de sentido común
Es posible que los datos de entrenamiento del mundo real no representen suficientemente los datos del tiempo de ejecución. Las soluciones de aprendizaje automático flexibles, como las DNN o los bosques, a menudo actúan de forma inesperada e incluso desenfrenada en partes del espacio de entrada que no están cubiertas por los datos de entrenamiento. Este comportamiento es especialmente problemático cuando se pueden violar restricciones políticas o de equidad.
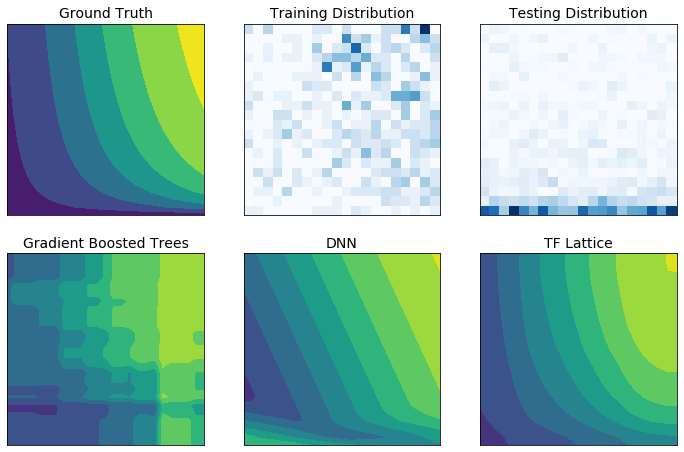
Aunque las formas comunes de regularización pueden dar como resultado una extrapolación más sensata, los regularizadores estándar no pueden garantizar un comportamiento razonable del modelo en todo el espacio de entrada, especialmente con entradas de alta dimensión. Cambiar a modelos más simples con un comportamiento más controlado y predecible puede tener un costo severo para la precisión del modelo.
TF Lattice permite seguir utilizando modelos flexibles, pero proporciona varias opciones para inyectar conocimiento del dominio en el proceso de aprendizaje a través de restricciones de forma semánticamente significativas, de sentido común o impulsadas por políticas:
- Monotonicidad : puede especificar que la salida solo debe aumentar/disminuir con respecto a una entrada. En nuestro ejemplo, es posible que desee especificar que una mayor distancia a una cafetería solo debería disminuir la preferencia prevista del usuario.
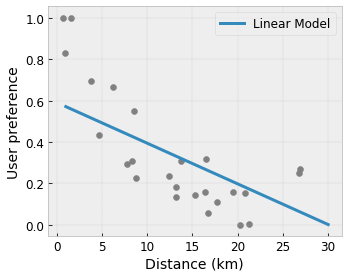
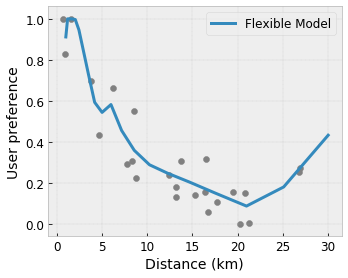
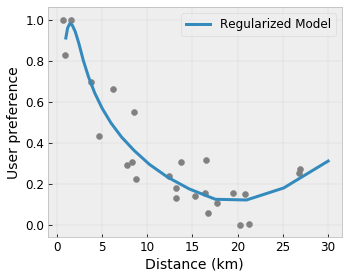
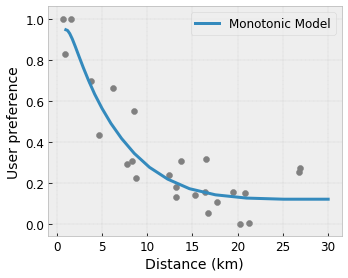
Convexidad/Concavidad : puede especificar que la forma de la función puede ser convexa o cóncava. Combinado con la monotonicidad, esto puede obligar a la función a representar rendimientos decrecientes con respecto a una característica determinada.
Unimodalidad : puede especificar que la función debe tener un pico único o un valle único. Esto le permite representar funciones que tienen un punto óptimo con respecto a una característica.
Confianza por pares : esta restricción funciona en un par de características y sugiere que una característica de entrada refleja semánticamente la confianza en otra característica. Por ejemplo, un mayor número de reseñas le da más confianza en la calificación promedio de estrellas de un restaurante. El modelo será más sensible con respecto a la calificación de estrellas (es decir, tendrá una mayor pendiente con respecto a la calificación) cuando el número de reseñas sea mayor.
Flexibilidad controlada con regularizadores
Además de las restricciones de forma, la red TensorFlow proporciona una serie de regularizadores para controlar la flexibilidad y suavidad de la función para cada capa.
Regularizador laplaciano : las salidas de la red/vértices de calibración/puntos clave se regularizan hacia los valores de sus respectivos vecinos. Esto da como resultado una función más plana .
Regularizador de Hesse : penaliza la primera derivada de la capa de calibración PWL para hacer la función más lineal .
Regularizador de arrugas : Penaliza la segunda derivada de la capa de calibración PWL para evitar cambios bruscos en la curvatura. Hace que la función sea más fluida.
Regularizador de torsión : las salidas de la red se regularizarán para evitar la torsión entre las funciones. En otras palabras, el modelo se regularizará hacia la independencia entre las contribuciones de las características.
Mezclar y combinar con otras capas de Keras.
Puede utilizar capas TF Lattice en combinación con otras capas de Keras para construir modelos parcialmente restringidos o regularizados. Por ejemplo, se pueden usar capas de calibración de celosía o PWL en la última capa de redes más profundas que incluyen incrustaciones u otras capas de Keras.
Papeles
- Ética deontológica por restricciones de forma de monotonicidad , Serena Wang, Maya Gupta, Conferencia Internacional sobre Inteligencia Artificial y Estadística (AISTATS), 2020
- Restricciones de forma para funciones de conjunto , Andrew Cotter, Maya Gupta, H. Jiang, Erez Louidor, Jim Muller, Taman Narayan, Serena Wang, Tao Zhu. Conferencia internacional sobre aprendizaje automático (ICML), 2019
- Los rendimientos decrecientes dan forma a las restricciones para la interpretabilidad y la regularización , Maya Gupta, Dara Bahri, Andrew Cotter, Kevin Canini, Avances en los sistemas de procesamiento de información neuronal (NeurIPS), 2018
- Redes de celosía profunda y funciones monotónicas parciales , Seungil You, Kevin Canini, David Ding, Jan Pfeifer, Maya R. Gupta, Avances en sistemas de procesamiento de información neuronal (NeurIPS), 2017
- Funciones monótonas rápidas y flexibles con conjuntos de celosías , Mahdi Milani Fard, Kevin Canini, Andrew Cotter, Jan Pfeifer, Maya Gupta, Avances en sistemas de procesamiento de información neuronal (NeurIPS), 2016
- Tablas de búsqueda interpoladas calibradas monótonas , Maya Gupta, Andrew Cotter, Jan Pfeifer, Konstantin Voevodski, Kevin Canini, Alexander Mangylov, Wojciech Moczydlowski, Alexander van Esbroeck, Journal of Machine Learning Research (JMLR), 2016
- Regresión optimizada para una evaluación de funciones eficiente , Eric García, Raman Arora, Maya R. Gupta, IEEE Transactions on Image Processing, 2012
- Regresión de celosía , Eric García, Maya Gupta, Avances en sistemas de procesamiento de información neuronal (NeurIPS), 2009
Tutoriales y documentos API
Para arquitecturas de modelos comunes, puede utilizar modelos prefabricados de Keras . También puede crear modelos personalizados utilizando capas de TF Lattice Keras o mezclarlos y combinarlos con otras capas de Keras. Consulte los documentos completos de la API para obtener más detalles.
,TensorFlow Lattice es una biblioteca que implementa modelos basados en celosías flexibles, controlados e interpretables. La biblioteca le permite inyectar conocimiento del dominio en el proceso de aprendizaje a través de restricciones de forma impulsadas por políticas o de sentido común. Esto se hace utilizando una colección de capas de Keras que pueden satisfacer restricciones como monotonicidad, convexidad y confianza por pares. La biblioteca también proporciona modelos prefabricados fáciles de configurar.
Conceptos
Esta sección es una versión simplificada de la descripción en Tablas de búsqueda interpoladas calibradas monotónicas , JMLR 2016.
Celosías
Una celosía es una tabla de búsqueda interpolada que puede aproximarse a relaciones arbitrarias de entrada-salida en sus datos. Superpone una cuadrícula regular en su espacio de entrada y aprende valores para la salida en los vértices de la cuadrícula. Para un punto de prueba \(x\), \(f(x)\) se interpola linealmente a partir de los valores de red que rodean \(x\).

El ejemplo simple anterior es una función con 2 características de entrada y 4 parámetros:\(\theta=[0, 0.2, 0.4, 1]\), que son los valores de la función en las esquinas del espacio de entrada; el resto de la función se interpola a partir de estos parámetros.
la funcion \(f(x)\) Puede capturar interacciones no lineales entre características. Puede pensar en los parámetros de la red como la altura de los postes colocados en el suelo en una cuadrícula regular, y la función resultante es como una tela apretada contra los cuatro postes.
Con \(D\) características y 2 vértices a lo largo de cada dimensión, una red regular tendrá \(2^D\) parámetros. Para ajustar una función más flexible, puede especificar una red más fina sobre el espacio de características con más vértices a lo largo de cada dimensión. Las funciones de regresión reticular son continuas e infinitamente diferenciables por partes.
Calibración
Digamos que el ejemplo de celosía anterior representa la felicidad de un usuario aprendido con una cafetería local sugerida calculada utilizando características:
- Precio del café, en el rango de 0 a 20 dólares.
- distancia al usuario, en el rango de 0 a 30 kilómetros
Queremos que nuestro modelo aprenda sobre la felicidad del usuario con una sugerencia de cafetería local. Los modelos de TensorFlow Lattice pueden usar funciones lineales por partes (con tfl.layers.PWLCalibration ) para calibrar y normalizar las características de entrada al rango aceptado por la red: 0,0 a 1,0 en la red de ejemplo anterior. A continuación se muestran ejemplos de funciones de calibraciones con 10 puntos clave:


A menudo es una buena idea utilizar los cuantiles de las características como puntos clave de entrada. Los modelos prediseñados de TensorFlow Lattice pueden establecer automáticamente los puntos clave de entrada en los cuantiles de características.
Para funciones categóricas, TensorFlow Lattice proporciona calibración categórica (con tfl.layers.CategoricalCalibration ) con límites de salida similares para alimentar una red.
conjuntos
La cantidad de parámetros de una capa reticular aumenta exponencialmente con la cantidad de características de entrada, por lo que no se escala bien a dimensiones muy altas. Para superar esta limitación, TensorFlow Lattice ofrece conjuntos de celosías que combinan (en promedio) varias celosías pequeñas , lo que permite que el modelo crezca linealmente en el número de características.
La biblioteca ofrece dos variaciones de estos conjuntos:
Random Tiny Lattices (RTL): cada submodelo utiliza un subconjunto aleatorio de características (con reemplazo).
Crystals : el algoritmo Crystals primero entrena un modelo de preajuste que estima las interacciones de características por pares. Luego organiza el conjunto final de manera que las entidades con más interacciones no lineales estén en las mismas redes.
¿Por qué TensorFlow Lattice?
Puede encontrar una breve introducción a TensorFlow Lattice en esta publicación del blog de TF .
Interpretabilidad
Dado que los parámetros de cada capa son la salida de esa capa, es fácil analizar, comprender y depurar cada parte del modelo.
Modelos precisos y flexibles
Usando celosías de grano fino, puede obtener funciones arbitrariamente complejas con una sola capa de celosía. El uso de múltiples capas de calibradores y redes a menudo funciona bien en la práctica y puede igualar o superar a los modelos DNN de tamaños similares.
Restricciones de forma de sentido común
Es posible que los datos de entrenamiento del mundo real no representen suficientemente los datos del tiempo de ejecución. Las soluciones de aprendizaje automático flexibles, como las DNN o los bosques, a menudo actúan de forma inesperada e incluso desenfrenada en partes del espacio de entrada que no están cubiertas por los datos de entrenamiento. Este comportamiento es especialmente problemático cuando se pueden violar restricciones políticas o de equidad.

Aunque las formas comunes de regularización pueden dar como resultado una extrapolación más sensata, los regularizadores estándar no pueden garantizar un comportamiento razonable del modelo en todo el espacio de entrada, especialmente con entradas de alta dimensión. Cambiar a modelos más simples con un comportamiento más controlado y predecible puede tener un costo severo para la precisión del modelo.
TF Lattice permite seguir utilizando modelos flexibles, pero proporciona varias opciones para inyectar conocimiento del dominio en el proceso de aprendizaje a través de restricciones de forma semánticamente significativas, de sentido común o impulsadas por políticas:
- Monotonicidad : puede especificar que la salida solo debe aumentar/disminuir con respecto a una entrada. En nuestro ejemplo, es posible que desee especificar que una mayor distancia a una cafetería solo debería disminuir la preferencia prevista del usuario.




Convexidad/Concavidad : puede especificar que la forma de la función puede ser convexa o cóncava. Combinado con la monotonicidad, esto puede obligar a la función a representar rendimientos decrecientes con respecto a una característica determinada.
Unimodalidad : puede especificar que la función debe tener un pico único o un valle único. Esto le permite representar funciones que tienen un punto óptimo con respecto a una característica.
Confianza por pares : esta restricción funciona en un par de características y sugiere que una característica de entrada refleja semánticamente la confianza en otra característica. Por ejemplo, un mayor número de reseñas le da más confianza en la calificación promedio de estrellas de un restaurante. El modelo será más sensible con respecto a la calificación de estrellas (es decir, tendrá una mayor pendiente con respecto a la calificación) cuando el número de reseñas sea mayor.
Flexibilidad controlada con regularizadores
Además de las restricciones de forma, la red TensorFlow proporciona una serie de regularizadores para controlar la flexibilidad y suavidad de la función para cada capa.
Regularizador laplaciano : las salidas de la red/vértices de calibración/puntos clave se regularizan hacia los valores de sus respectivos vecinos. Esto da como resultado una función más plana .
Regularizador de Hesse : penaliza la primera derivada de la capa de calibración PWL para hacer la función más lineal .
Regularizador de arrugas : Penaliza la segunda derivada de la capa de calibración PWL para evitar cambios bruscos en la curvatura. Hace que la función sea más fluida.
Regularizador de torsión : las salidas de la red se regularizarán para evitar la torsión entre las funciones. En otras palabras, el modelo se regularizará hacia la independencia entre las contribuciones de las características.
Mezclar y combinar con otras capas de Keras.
Puede utilizar capas TF Lattice en combinación con otras capas de Keras para construir modelos parcialmente restringidos o regularizados. Por ejemplo, se pueden usar capas de calibración de celosía o PWL en la última capa de redes más profundas que incluyen incrustaciones u otras capas de Keras.
Papeles
- Ética deontológica por restricciones de forma de monotonicidad , Serena Wang, Maya Gupta, Conferencia Internacional sobre Inteligencia Artificial y Estadística (AISTATS), 2020
- Restricciones de forma para funciones de conjunto , Andrew Cotter, Maya Gupta, H. Jiang, Erez Louidor, Jim Muller, Taman Narayan, Serena Wang, Tao Zhu. Conferencia internacional sobre aprendizaje automático (ICML), 2019
- Los rendimientos decrecientes dan forma a las restricciones para la interpretabilidad y la regularización , Maya Gupta, Dara Bahri, Andrew Cotter, Kevin Canini, Avances en los sistemas de procesamiento de información neuronal (NeurIPS), 2018
- Redes de celosía profunda y funciones monotónicas parciales , Seungil You, Kevin Canini, David Ding, Jan Pfeifer, Maya R. Gupta, Avances en sistemas de procesamiento de información neuronal (NeurIPS), 2017
- Funciones monótonas rápidas y flexibles con conjuntos de celosías , Mahdi Milani Fard, Kevin Canini, Andrew Cotter, Jan Pfeifer, Maya Gupta, Avances en sistemas de procesamiento de información neuronal (NeurIPS), 2016
- Tablas de búsqueda interpoladas calibradas monótonas , Maya Gupta, Andrew Cotter, Jan Pfeifer, Konstantin Voevodski, Kevin Canini, Alexander Mangylov, Wojciech Moczydlowski, Alexander van Esbroeck, Journal of Machine Learning Research (JMLR), 2016
- Regresión optimizada para una evaluación de funciones eficiente , Eric García, Raman Arora, Maya R. Gupta, IEEE Transactions on Image Processing, 2012
- Regresión de celosía , Eric García, Maya Gupta, Avances en sistemas de procesamiento de información neuronal (NeurIPS), 2009
Tutoriales y documentos API
Para arquitecturas de modelos comunes, puede utilizar modelos prefabricados de Keras . También puede crear modelos personalizados utilizando capas de TF Lattice Keras o mezclarlos y combinarlos con otras capas de Keras. Consulte los documentos completos de la API para obtener más detalles.

