 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Zobacz na GitHub Zobacz na GitHub |  Pobierz notatnik Pobierz notatnik |  Zobacz model piasty TF Zobacz model piasty TF |
Ten Colab demonstruje użycie modułu TF Hub opartego na generatywnej sieci kontradyktoryjnej (GAN). Moduł odwzorowuje wektory N-wymiarowe, zwane przestrzenią utajoną, na obrazy RGB.
Podano dwa przykłady:
- Mapowanie z utajonego miejsca do zdjęć, a
- Biorąc pod uwagę obraz docelowy, używając gradientu zejście do znalezienia ukrytego wektor, który generuje obraz podobny do obrazu docelowego.
Opcjonalne warunki wstępne
- Znajomość niskopoziomowych Tensorflow pojęć .
- Generatywna kontradyktoryjności Network na Wikipedia.
- Papier na Progressive Gans: Progressive Uprawa Gans dla poprawy jakości, stabilności i zmienności .
Więcej modeli
Tutaj można znaleźć wszystkie modele aktualnie przechowywane na tfhub.dev które mogą generować obrazy.
Ustawiać
# Install imageio for creating animations.pip -q install imageiopip -q install scikit-imagepip install git+https://github.com/tensorflow/docs
Importy i definicje funkcji
from absl import logging
import imageio
import PIL.Image
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
tf.random.set_seed(0)
import tensorflow_hub as hub
from tensorflow_docs.vis import embed
import time
try:
from google.colab import files
except ImportError:
pass
from IPython import display
from skimage import transform
# We could retrieve this value from module.get_input_shapes() if we didn't know
# beforehand which module we will be using.
latent_dim = 512
# Interpolates between two vectors that are non-zero and don't both lie on a
# line going through origin. First normalizes v2 to have the same norm as v1.
# Then interpolates between the two vectors on the hypersphere.
def interpolate_hypersphere(v1, v2, num_steps):
v1_norm = tf.norm(v1)
v2_norm = tf.norm(v2)
v2_normalized = v2 * (v1_norm / v2_norm)
vectors = []
for step in range(num_steps):
interpolated = v1 + (v2_normalized - v1) * step / (num_steps - 1)
interpolated_norm = tf.norm(interpolated)
interpolated_normalized = interpolated * (v1_norm / interpolated_norm)
vectors.append(interpolated_normalized)
return tf.stack(vectors)
# Simple way to display an image.
def display_image(image):
image = tf.constant(image)
image = tf.image.convert_image_dtype(image, tf.uint8)
return PIL.Image.fromarray(image.numpy())
# Given a set of images, show an animation.
def animate(images):
images = np.array(images)
converted_images = np.clip(images * 255, 0, 255).astype(np.uint8)
imageio.mimsave('./animation.gif', converted_images)
return embed.embed_file('./animation.gif')
logging.set_verbosity(logging.ERROR)
Interpolacja przestrzeni utajonej
Wektory losowe
Interpolacja przestrzeni utajonej między dwoma losowo zainicjowanymi wektorami. Będziemy korzystać z modułu TF Hub progan-128 , który zawiera wstępnie przeszkolony Progressive Gan.
progan = hub.load("https://tfhub.dev/google/progan-128/1").signatures['default']
def interpolate_between_vectors():
v1 = tf.random.normal([latent_dim])
v2 = tf.random.normal([latent_dim])
# Creates a tensor with 25 steps of interpolation between v1 and v2.
vectors = interpolate_hypersphere(v1, v2, 50)
# Uses module to generate images from the latent space.
interpolated_images = progan(vectors)['default']
return interpolated_images
interpolated_images = interpolate_between_vectors()
animate(interpolated_images)

Znajdowanie najbliższego wektora w przestrzeni utajonej
Napraw obraz docelowy. Jako przykład użyj obrazu wygenerowanego z modułu lub wgraj własny.
image_from_module_space = True # @param { isTemplate:true, type:"boolean" }
def get_module_space_image():
vector = tf.random.normal([1, latent_dim])
images = progan(vector)['default'][0]
return images
def upload_image():
uploaded = files.upload()
image = imageio.imread(uploaded[list(uploaded.keys())[0]])
return transform.resize(image, [128, 128])
if image_from_module_space:
target_image = get_module_space_image()
else:
target_image = upload_image()
display_image(target_image)

Po zdefiniowaniu funkcji straty między obrazem docelowym a obrazem wygenerowanym przez zmienną przestrzeni latentnej, możemy użyć gradientu zejścia, aby znaleźć wartości zmiennych, które minimalizują stratę.
tf.random.set_seed(42)
initial_vector = tf.random.normal([1, latent_dim])
display_image(progan(initial_vector)['default'][0])

def find_closest_latent_vector(initial_vector, num_optimization_steps,
steps_per_image):
images = []
losses = []
vector = tf.Variable(initial_vector)
optimizer = tf.optimizers.Adam(learning_rate=0.01)
loss_fn = tf.losses.MeanAbsoluteError(reduction="sum")
for step in range(num_optimization_steps):
if (step % 100)==0:
print()
print('.', end='')
with tf.GradientTape() as tape:
image = progan(vector.read_value())['default'][0]
if (step % steps_per_image) == 0:
images.append(image.numpy())
target_image_difference = loss_fn(image, target_image[:,:,:3])
# The latent vectors were sampled from a normal distribution. We can get
# more realistic images if we regularize the length of the latent vector to
# the average length of vector from this distribution.
regularizer = tf.abs(tf.norm(vector) - np.sqrt(latent_dim))
loss = target_image_difference + regularizer
losses.append(loss.numpy())
grads = tape.gradient(loss, [vector])
optimizer.apply_gradients(zip(grads, [vector]))
return images, losses
num_optimization_steps=200
steps_per_image=5
images, loss = find_closest_latent_vector(initial_vector, num_optimization_steps, steps_per_image)
.................................................................................................... ....................................................................................................
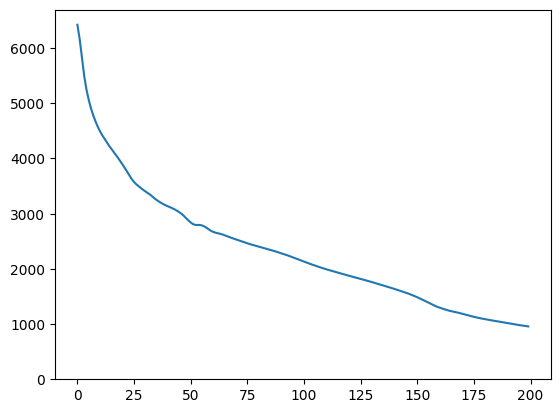
plt.plot(loss)
plt.ylim([0,max(plt.ylim())])
(0.0, 6696.301751708985)
animate(np.stack(images))

Porównaj wynik z celem:
display_image(np.concatenate([images[-1], target_image], axis=1))

Zabawa z powyższym przykładem
Jeśli obraz pochodzi z przestrzeni modułu, zejście jest szybkie i zbiega się do rozsądnej próbki. Wypróbuj malejącym do obrazu, który nie jest z przestrzeni modułu. Zejście zbiegnie się tylko wtedy, gdy obraz będzie dość blisko przestrzeni obrazów treningowych.
Jak sprawić, by schodziła szybciej i do bardziej realistycznego obrazu? Można spróbować:
- stosując różne straty na różnicy obrazu, np. kwadratowe,
- używanie innego regularizera na wektorze utajonym,
- inicjowanie z losowego wektora w wielu przebiegach,
- itp.
