Explorando o TF-Hub CORD-19 Swivel Embeddings

Ver no TensorFlow.org Executar no Google Colab Ver no GitHub Baixar caderno Veja o modelo TF Hub

O texto CORD-19 Swivel incorporando módulo de TF-Hub ( https://tfhub.dev/tensorflow/cord-19/swivel-128d/3 ) foi construído para pesquisadores de apoio analisando texto línguas naturais relacionadas com COVID-19. Estas incorporações foram treinados sobre os títulos, autores, resumos, textos do corpo, e os títulos de referência de artigos no conjunto de dados CORD-19 .

Nesta colab iremos:

  • Analise palavras semanticamente semelhantes no espaço de incorporação
  • Treine um classificador no conjunto de dados SciCite usando os embeddings CORD-19

Configurar

import functools
import itertools
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd

import tensorflow as tf

import tensorflow_datasets as tfds
import tensorflow_hub as hub

from tqdm import trange

Analise os embeddings

Vamos começar analisando a incorporação, calculando e plotando uma matriz de correlação entre os diferentes termos. Se o embedding aprender a capturar com sucesso o significado de palavras diferentes, os vetores de embedding de palavras semanticamente semelhantes devem estar próximos. Vamos dar uma olhada em alguns termos relacionados ao COVID-19.

# Use the inner product between two embedding vectors as the similarity measure
def plot_correlation(labels, features):
  corr = np.inner(features, features)
  corr /= np.max(corr)
  sns.heatmap(corr, xticklabels=labels, yticklabels=labels)

# Generate embeddings for some terms
queries = [
  # Related viruses
  'coronavirus', 'SARS', 'MERS',
  # Regions
  'Italy', 'Spain', 'Europe',
  # Symptoms
  'cough', 'fever', 'throat'
]

module = hub.load('https://tfhub.dev/tensorflow/cord-19/swivel-128d/3')
embeddings = module(queries)

plot_correlation(queries, embeddings)

png

Podemos ver que a incorporação capturou com sucesso o significado dos diferentes termos. Cada palavra é semelhante às outras palavras do seu cluster (ou seja, "coronavirus" altamente correlacionado com "SARS" e "MERS"), embora sejam diferentes dos termos de outros clusters (ou seja, a semelhança entre "SARS" e "Espanha" é próximo a 0).

Agora vamos ver como podemos usar esses embeddings para resolver uma tarefa específica.

SciCite: Classificação da intenção de citação

Esta seção mostra como se pode usar a incorporação para tarefas posteriores, como classificação de texto. Nós vamos usar o dataset SciCite de TensorFlow conjuntos de dados a intenções de citação classifico em trabalhos acadêmicos. Dada uma frase com uma citação de um artigo acadêmico, classifique se o objetivo principal da citação é como informação de base, uso de métodos ou comparação de resultados.

builder = tfds.builder(name='scicite')
builder.download_and_prepare()
train_data, validation_data, test_data = builder.as_dataset(
    split=('train', 'validation', 'test'),
    as_supervised=True)

Vamos dar uma olhada em alguns exemplos rotulados do conjunto de treinamento

Treinando um classificador de intenção de citaton

Vamos treinar um classificador no conjunto de dados SciCite usando Keras. Vamos construir um modelo que use os embeddings CORD-19 com uma camada de classificação no topo.

Hiperparâmetros

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 keras_layer (KerasLayer)    (None, 128)               17301632  
                                                                 
 dense (Dense)               (None, 3)                 387       
                                                                 
=================================================================
Total params: 17,302,019
Trainable params: 387
Non-trainable params: 17,301,632
_________________________________________________________________

Treine e avalie o modelo

Vamos treinar e avaliar o modelo para ver o desempenho na tarefa SciCite

EPOCHS = 35
BATCH_SIZE = 32

history = model.fit(train_data.shuffle(10000).batch(BATCH_SIZE),
                    epochs=EPOCHS,
                    validation_data=validation_data.batch(BATCH_SIZE),
                    verbose=1)

Epoch 1/35
257/257 [==============================] - 3s 7ms/step - loss: 0.9244 - accuracy: 0.5924 - val_loss: 0.7915 - val_accuracy: 0.6627
Epoch 2/35
257/257 [==============================] - 2s 5ms/step - loss: 0.7097 - accuracy: 0.7152 - val_loss: 0.6799 - val_accuracy: 0.7358
Epoch 3/35
257/257 [==============================] - 2s 7ms/step - loss: 0.6317 - accuracy: 0.7551 - val_loss: 0.6285 - val_accuracy: 0.7544
Epoch 4/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5938 - accuracy: 0.7687 - val_loss: 0.6032 - val_accuracy: 0.7566
Epoch 5/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5724 - accuracy: 0.7750 - val_loss: 0.5871 - val_accuracy: 0.7653
Epoch 6/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5580 - accuracy: 0.7825 - val_loss: 0.5800 - val_accuracy: 0.7653
Epoch 7/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5484 - accuracy: 0.7870 - val_loss: 0.5711 - val_accuracy: 0.7718
Epoch 8/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5417 - accuracy: 0.7896 - val_loss: 0.5648 - val_accuracy: 0.7806
Epoch 9/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5356 - accuracy: 0.7902 - val_loss: 0.5628 - val_accuracy: 0.7740
Epoch 10/35
257/257 [==============================] - 2s 7ms/step - loss: 0.5313 - accuracy: 0.7903 - val_loss: 0.5581 - val_accuracy: 0.7849
Epoch 11/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5277 - accuracy: 0.7928 - val_loss: 0.5555 - val_accuracy: 0.7838
Epoch 12/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5242 - accuracy: 0.7940 - val_loss: 0.5528 - val_accuracy: 0.7849
Epoch 13/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5215 - accuracy: 0.7947 - val_loss: 0.5522 - val_accuracy: 0.7828
Epoch 14/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5190 - accuracy: 0.7961 - val_loss: 0.5527 - val_accuracy: 0.7751
Epoch 15/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5176 - accuracy: 0.7940 - val_loss: 0.5492 - val_accuracy: 0.7806
Epoch 16/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5154 - accuracy: 0.7978 - val_loss: 0.5500 - val_accuracy: 0.7817
Epoch 17/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5136 - accuracy: 0.7968 - val_loss: 0.5488 - val_accuracy: 0.7795
Epoch 18/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5127 - accuracy: 0.7967 - val_loss: 0.5504 - val_accuracy: 0.7838
Epoch 19/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5111 - accuracy: 0.7970 - val_loss: 0.5470 - val_accuracy: 0.7860
Epoch 20/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5101 - accuracy: 0.7972 - val_loss: 0.5471 - val_accuracy: 0.7871
Epoch 21/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5082 - accuracy: 0.7997 - val_loss: 0.5483 - val_accuracy: 0.7784
Epoch 22/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5077 - accuracy: 0.7995 - val_loss: 0.5471 - val_accuracy: 0.7860
Epoch 23/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5064 - accuracy: 0.8012 - val_loss: 0.5439 - val_accuracy: 0.7871
Epoch 24/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5057 - accuracy: 0.7990 - val_loss: 0.5476 - val_accuracy: 0.7882
Epoch 25/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5050 - accuracy: 0.7996 - val_loss: 0.5442 - val_accuracy: 0.7937
Epoch 26/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5045 - accuracy: 0.7999 - val_loss: 0.5455 - val_accuracy: 0.7860
Epoch 27/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5032 - accuracy: 0.7991 - val_loss: 0.5435 - val_accuracy: 0.7893
Epoch 28/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5034 - accuracy: 0.8022 - val_loss: 0.5431 - val_accuracy: 0.7882
Epoch 29/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5025 - accuracy: 0.8017 - val_loss: 0.5441 - val_accuracy: 0.7937
Epoch 30/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5017 - accuracy: 0.8013 - val_loss: 0.5463 - val_accuracy: 0.7838
Epoch 31/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5015 - accuracy: 0.8017 - val_loss: 0.5453 - val_accuracy: 0.7871
Epoch 32/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5011 - accuracy: 0.8014 - val_loss: 0.5448 - val_accuracy: 0.7915
Epoch 33/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5006 - accuracy: 0.8025 - val_loss: 0.5432 - val_accuracy: 0.7893
Epoch 34/35
257/257 [==============================] - 2s 5ms/step - loss: 0.5005 - accuracy: 0.8008 - val_loss: 0.5448 - val_accuracy: 0.7904
Epoch 35/35
257/257 [==============================] - 2s 5ms/step - loss: 0.4996 - accuracy: 0.8016 - val_loss: 0.5448 - val_accuracy: 0.7915

from matplotlib import pyplot as plt
def display_training_curves(training, validation, title, subplot):
  if subplot%10==1: # set up the subplots on the first call
    plt.subplots(figsize=(10,10), facecolor='#F0F0F0')
    plt.tight_layout()
  ax = plt.subplot(subplot)
  ax.set_facecolor('#F8F8F8')
  ax.plot(training)
  ax.plot(validation)
  ax.set_title('model '+ title)
  ax.set_ylabel(title)
  ax.set_xlabel('epoch')
  ax.legend(['train', 'valid.'])

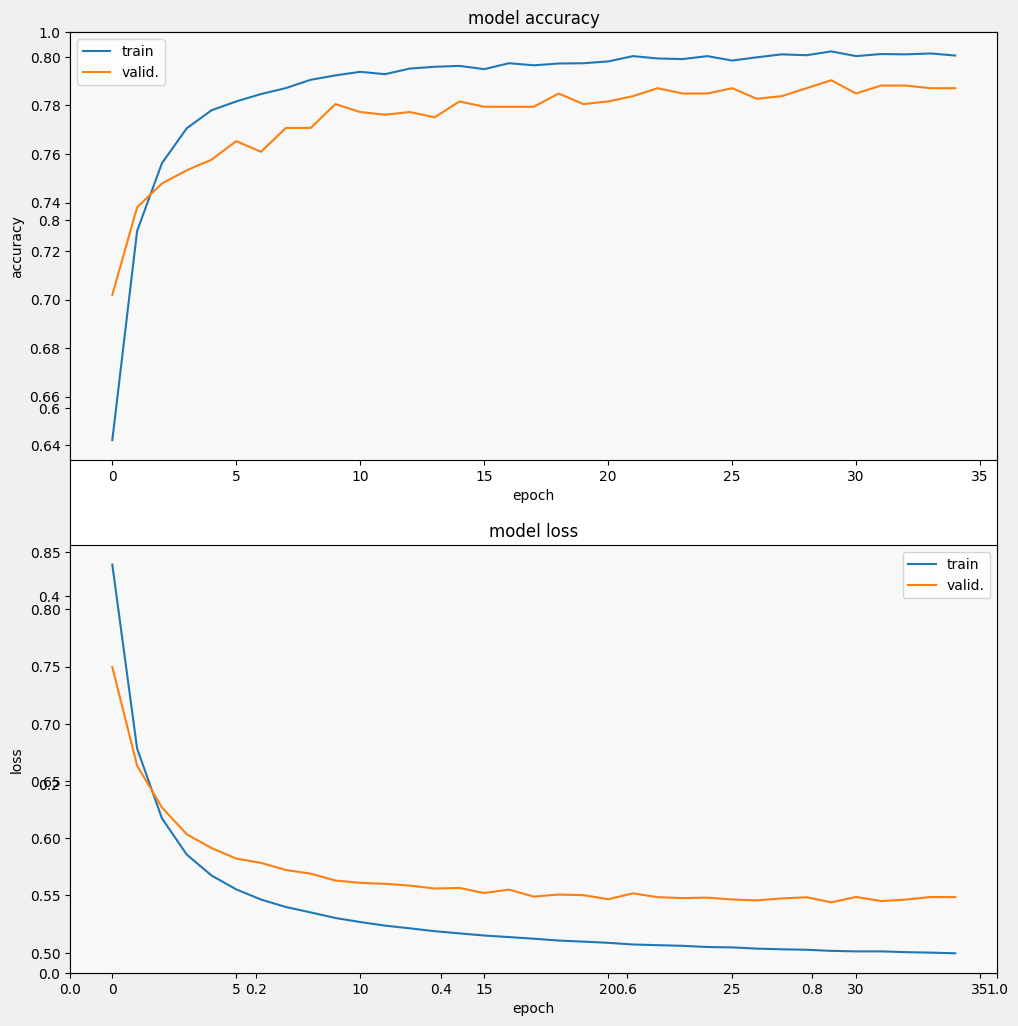
display_training_curves(history.history['accuracy'], history.history['val_accuracy'], 'accuracy', 211)
display_training_curves(history.history['loss'], history.history['val_loss'], 'loss', 212)

png

Avalie o modelo

E vamos ver como o modelo funciona. Dois valores serão retornados. Perda (um número que representa nosso erro, valores mais baixos são melhores) e precisão.

results = model.evaluate(test_data.batch(512), verbose=2)

for name, value in zip(model.metrics_names, results):
  print('%s: %.3f' % (name, value))

4/4 - 0s - loss: 0.5357 - accuracy: 0.7891 - 441ms/epoch - 110ms/step
loss: 0.536
accuracy: 0.789

Podemos ver que a perda diminui rapidamente enquanto, especialmente, a precisão aumenta rapidamente. Vamos plotar alguns exemplos para verificar como a previsão se relaciona com os rótulos verdadeiros:

prediction_dataset = next(iter(test_data.batch(20)))

prediction_texts = [ex.numpy().decode('utf8') for ex in prediction_dataset[0]]
prediction_labels = [label2str(x) for x in prediction_dataset[1]]

predictions = [
    label2str(x) for x in np.argmax(model.predict(prediction_texts), axis=-1)]


pd.DataFrame({
    TEXT_FEATURE_NAME: prediction_texts,
    LABEL_NAME: prediction_labels,
    'prediction': predictions
})

Podemos ver que, para essa amostra aleatória, o modelo prevê o rótulo correto na maioria das vezes, indicando que ele pode incorporar frases científicas muito bem.

Qual é o próximo?

Agora que você aprendeu um pouco mais sobre os embeddings CORD-19 Swivel do TF-Hub, incentivamos você a participar da competição CORD-19 Kaggle para contribuir com a obtenção de conhecimentos científicos de textos acadêmicos relacionados ao COVID-19.