 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看 |
 在 Google Colab 中运行 在 Google Colab 中运行 |
 在 GitHub 上查看源代码 在 GitHub 上查看源代码 |
 下载笔记本 下载笔记本 |
在前面的教程里,您已经了解了tensors, variables, gradient tape, 和modules。在这篇教程,您将把它们放在一起训练模型。
此外,TensorFlow 还包括 tf.Keras API,这是一种高级神经网络 API,可提供有用的抽象来减少样板。但是,在本指南中,您将使用基本类。
创建
import tensorflow as tf
import matplotlib.pyplot as plt
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
2022-12-14 20:11:29.211963: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer.so.7'; dlerror: libnvinfer.so.7: cannot open shared object file: No such file or directory 2022-12-14 20:11:29.212049: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer_plugin.so.7'; dlerror: libnvinfer_plugin.so.7: cannot open shared object file: No such file or directory 2022-12-14 20:11:29.212057: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Cannot dlopen some TensorRT libraries. If you would like to use Nvidia GPU with TensorRT, please make sure the missing libraries mentioned above are installed properly.
解决机器学习问题
解决一个机器学习问题通常包含以下步骤:
- 获得训练数据。
- 定义模型。
- 定义损失函数。
- 遍历训练数据,从目标值计算损失。
- 计算该损失的梯度,并使用optimizer调整变量以适合数据。
- 计算结果。
为了便于说明,在本指南中,您将开发一个简单的线性模型, \(f(x) = x * W + b\), 其中包含两个变量: \(W\) (权重) 和 \(b\) (偏差)。
这是最基本的机器学习问题:给定 \(x\) 和 \(y\),尝试通过简单的线性回归来找到直线的斜率和偏移量。
数据
监督学习使用输入(通常表示为 x)和输出(表示为 y,通常称为标签)。目标是从成对的输入和输出中学习,以便您可以根据输入预测输出的值。
TensorFlow中几乎每个输入数据都是由张量表示,并且通常是向量。监督学习中,输出(即想到预测值)同样是个张量。
下面是通过将高斯(正态)噪声添加到直线上的点而合成的一些数据。
# The actual line
TRUE_W = 3.0
TRUE_B = 2.0
NUM_EXAMPLES = 201
# A vector of random x values
x = tf.linspace(-2,2, NUM_EXAMPLES)
x = tf.cast(x, tf.float32)
def f(x):
return x * TRUE_W + TRUE_B
# Generate some noise
noise = tf.random.normal(shape=[NUM_EXAMPLES])
# Calculate y
y = f(x) + noise
# Plot all the data
plt.plot(x, y, '.')
plt.show()
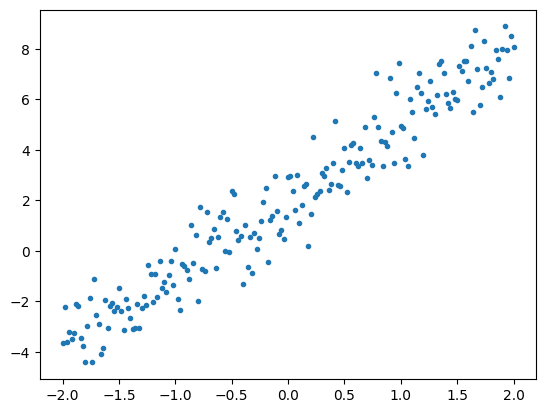
张量通常以 batches 的形式聚集在一起,或者是成组的输入和输出堆叠在一起。批处理能够对训练过程带来一些好处,并且可以与加速器和矢量化计算很好地配合使用。给定此数据集的大小,您可以将整个数据集视为一个批次。
定义模型
使用 tf.Variable 代表模型中的所有权重。tf.Variable 能够存储值,并根据需要以张量形式提供它。详情请见 variable guide。
使用 tf.Module 封装变量和计算。您可以使用任何Python对象,但是通过这种方式可以轻松保存它。
这里,您可以定义 w 和 b 为变量。
class MyModel(tf.Module):
def __init__(self, **kwargs):
super().__init__(**kwargs)
# Initialize the weights to `5.0` and the bias to `0.0`
# In practice, these should be randomly initialized
self.w = tf.Variable(5.0)
self.b = tf.Variable(0.0)
def __call__(self, x):
return self.w * x + self.b
model = MyModel()
# List the variables tf.modules's built-in variable aggregation.
print("Variables:", model.variables)
# Verify the model works
assert model(3.0).numpy() == 15.0
Variables: (<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'Variable:0' shape=() dtype=float32, numpy=5.0>)
初始变量在此处以固定方式设置,但 Keras 提供了您可以与或不与 Keras 其他部分一起使用的许多初始值设定项。
定义损失函数
损失函数衡量给定输入的模型输出与目标输出的匹配程度。目的是在训练过程中尽量减少这种差异。定义标准的L2损失,也称为“均方误差”:
# This computes a single loss value for an entire batch
def loss(target_y, predicted_y):
return tf.reduce_mean(tf.square(target_y - predicted_y))
在训练模型之前,您可以可视化损失值。使用红色绘制模型的预测值,使用蓝色绘制训练数据。
plt.plot(x, y, '.', label="Data")
plt.plot(x, f(x), label="Ground truth")
plt.plot(x, model(x), label="Predictions")
plt.legend()
plt.show()
print("Current loss: %1.6f" % loss(y, model(x)).numpy())
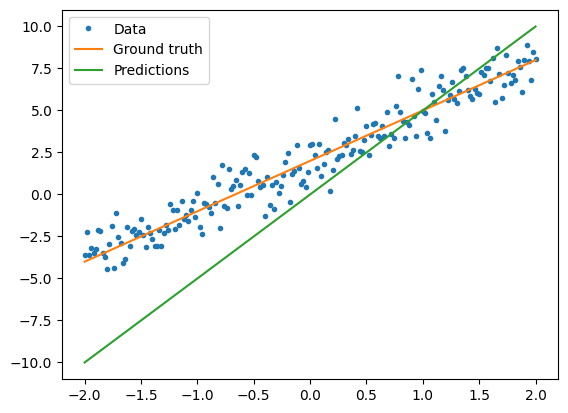
Current loss: 10.730574
定义训练循环
训练循环按顺序重复执行以下任务:
- 发送一批输入值,通过模型生成输出值
- 通过比较输出值与输出(标签),来计算损失值
- 使用梯度带(GradientTape)找到梯度值
- 使用这些梯度优化变量
这个例子中,您可以使用 gradient descent训练数据。
tf.keras.optimizers中有许多梯度下降的变量。但是本着搭建的第一原则,您将在这里 借助tf.GradientTape的自动微分和tf.assign_sub的递减值(结合了tf.assign和tf.sub)自己实现基本数学:
# Given a callable model, inputs, outputs, and a learning rate...
def train(model, x, y, learning_rate):
with tf.GradientTape() as t:
# Trainable variables are automatically tracked by GradientTape
current_loss = loss(y, model(x))
# Use GradientTape to calculate the gradients with respect to W and b
dw, db = t.gradient(current_loss, [model.w, model.b])
# Subtract the gradient scaled by the learning rate
model.w.assign_sub(learning_rate * dw)
model.b.assign_sub(learning_rate * db)
要查看训练,您可以通过训练循环发送同一批次的 x 和 y,并观察 W 和 b 如何变化。
model = MyModel()
# Collect the history of W-values and b-values to plot later
weights = []
biases = []
epochs = range(10)
# Define a training loop
def report(model, loss):
return f"W = {model.w.numpy():1.2f}, b = {model.b.numpy():1.2f}, loss={loss:2.5f}"
def training_loop(model, x, y):
for epoch in epochs:
# Update the model with the single giant batch
train(model, x, y, learning_rate=0.1)
# Track this before I update
weights.append(model.w.numpy())
biases.append(model.b.numpy())
current_loss = loss(y, model(x))
print(f"Epoch {epoch:2d}:")
print(" ", report(model, current_loss))
进行训练
current_loss = loss(y, model(x))
print(f"Starting:")
print(" ", report(model, current_loss))
training_loop(model, x, y)
Starting:
W = 5.00, b = 0.00, loss=10.73057
Epoch 0:
W = 4.45, b = 0.41, loss=6.58578
Epoch 1:
W = 4.05, b = 0.74, loss=4.21202
Epoch 2:
W = 3.75, b = 1.00, loss=2.84173
Epoch 3:
W = 3.54, b = 1.21, loss=2.04423
Epoch 4:
W = 3.38, b = 1.38, loss=1.57628
Epoch 5:
W = 3.27, b = 1.51, loss=1.29945
Epoch 6:
W = 3.18, b = 1.62, loss=1.13437
Epoch 7:
W = 3.12, b = 1.71, loss=1.03518
Epoch 8:
W = 3.08, b = 1.78, loss=0.97515
Epoch 9:
W = 3.04, b = 1.83, loss=0.93857
下面是权重随时间的演变:
plt.plot(epochs, weights, label='Weights', color=colors[0])
plt.plot(epochs, [TRUE_W] * len(epochs), '--',
label = "True weight", color=colors[0])
plt.plot(epochs, biases, label='bias', color=colors[1])
plt.plot(epochs, [TRUE_B] * len(epochs), "--",
label="True bias", color=colors[1])
plt.legend()
plt.show()
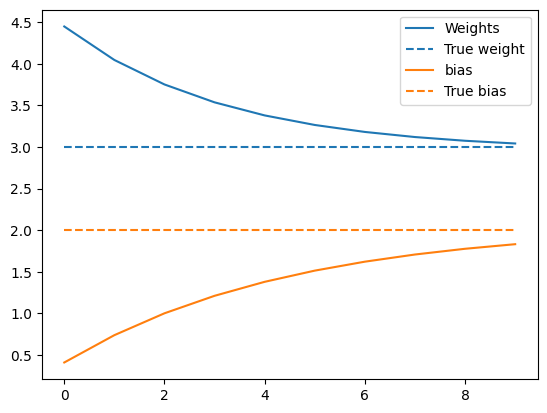
呈现训练的模型的性能
plt.plot(x, y, '.', label="Data")
plt.plot(x, f(x), label="Ground truth")
plt.plot(x, model(x), label="Predictions")
plt.legend()
plt.show()
print("Current loss: %1.6f" % loss(model(x), y).numpy())
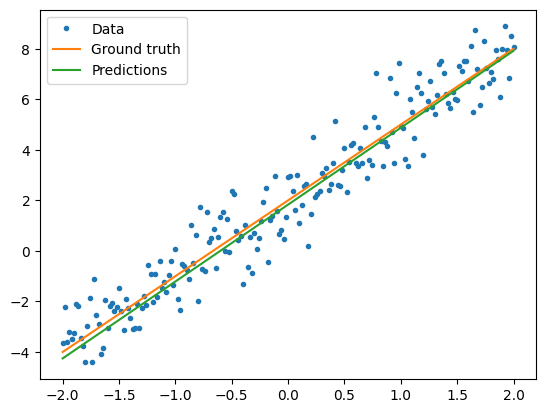
Current loss: 0.938567
使用Keras完成相同的解决方案
将上面的代码与Keras中的等效代码进行对比很有用。
如果您将tf.keras.Model子类化,则定义模型与其看起来完全相同。请记住,Keras模型最终从模块继承。
class MyModelKeras(tf.keras.Model):
def __init__(self, **kwargs):
super().__init__(**kwargs)
# Initialize the weights to `5.0` and the bias to `0.0`
# In practice, these should be randomly initialized
self.w = tf.Variable(5.0)
self.b = tf.Variable(0.0)
def call(self, x):
return self.w * x + self.b
keras_model = MyModelKeras()
# Reuse the training loop with a Keras model
training_loop(keras_model, x, y)
# You can also save a checkpoint using Keras's built-in support
keras_model.save_weights("my_checkpoint")
Epoch 0:
W = 4.45, b = 0.41, loss=6.58578
Epoch 1:
W = 4.05, b = 0.74, loss=4.21202
Epoch 2:
W = 3.75, b = 1.00, loss=2.84173
Epoch 3:
W = 3.54, b = 1.21, loss=2.04423
Epoch 4:
W = 3.38, b = 1.38, loss=1.57628
Epoch 5:
W = 3.27, b = 1.51, loss=1.29945
Epoch 6:
W = 3.18, b = 1.62, loss=1.13437
Epoch 7:
W = 3.12, b = 1.71, loss=1.03518
Epoch 8:
W = 3.08, b = 1.78, loss=0.97515
Epoch 9:
W = 3.04, b = 1.83, loss=0.93857
您可以使用Keras的内置功能作为捷径,而不必在每次创建模型时都编写新的训练循环。当您不想编写或调试Python训练循环时,这很有用。
如果您使用Keras,您将会需要使用 model.compile() 去设置参数, 使用model.fit() 进行训练。借助Keras实现L2损失和梯度下降需要的代码量更少,就像一个捷径。Keras损失和优化器也可以在这些便利功能之外使用,而前面的示例也可以使用它们。
keras_model = MyModelKeras()
# compile sets the training parameters
keras_model.compile(
# By default, fit() uses tf.function(). You can
# turn that off for debugging, but it is on now.
run_eagerly=False,
# Using a built-in optimizer, configuring as an object
optimizer=tf.keras.optimizers.SGD(learning_rate=0.1),
# Keras comes with built-in MSE error
# However, you could use the loss function
# defined above
loss=tf.keras.losses.mean_squared_error,
)
Kerasfit期望批处理数据或完整的数据集作为NumPy数组。 NumPy数组分为多个批次,默认批次大小为32。
这一案例中,为了匹配手写训练循环,您应该以大小为1000的单批次传递x。
print(x.shape[0])
keras_model.fit(x, y, epochs=10, batch_size=1000)
201 Epoch 1/10 1/1 [==============================] - 0s 469ms/step - loss: 10.7306 Epoch 2/10 1/1 [==============================] - 0s 5ms/step - loss: 6.5858 Epoch 3/10 1/1 [==============================] - 0s 4ms/step - loss: 4.2120 Epoch 4/10 1/1 [==============================] - 0s 4ms/step - loss: 2.8417 Epoch 5/10 1/1 [==============================] - 0s 4ms/step - loss: 2.0442 Epoch 6/10 1/1 [==============================] - 0s 4ms/step - loss: 1.5763 Epoch 7/10 1/1 [==============================] - 0s 4ms/step - loss: 1.2994 Epoch 8/10 1/1 [==============================] - 0s 4ms/step - loss: 1.1344 Epoch 9/10 1/1 [==============================] - 0s 4ms/step - loss: 1.0352 Epoch 10/10 1/1 [==============================] - 0s 4ms/step - loss: 0.9751 <keras.callbacks.History at 0x7efc7de5ad90>
请注意,Keras会在训练后而不是之前打印出损失,因此第一次损失会显得较低。否则,这表明本质上相同的训练效果。
下一步
在这篇引导中,您已经看到怎样使用tensors, variables, modules, 和gradient tape去构建并训练模型,也进一步了解到这些是如何与Keras对应的。
但是,这是一个极其简单的问题。有关更实用的介绍,请参阅自定义训练演示。
有关使用内置 Keras 训练循环的更多信息,请参阅本指南。有关训练循环和 Keras 的更多信息,请参阅本指南。有关编写自定义分布式训练循环的信息,请参阅本指南。
