 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Différenciation automatique et dégradés
La différenciation automatique est utile pour implémenter des algorithmes d'apprentissage automatique tels que la rétropropagation pour la formation de réseaux de neurones.
Dans ce guide, vous explorerez les différentes manières de calculer les gradients avec TensorFlow, en particulier lors d' une exécution rapide .
Installer
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
Calcul des gradients
Pour différencier automatiquement, TensorFlow doit se rappeler quelles opérations se produisent dans quel ordre pendant le passage vers l' avant . Ensuite, lors de la passe arrière , TensorFlow parcourt cette liste d'opérations dans l'ordre inverse pour calculer les gradients.
Bandes dégradées
TensorFlow fournit l'API tf.GradientTape pour la différenciation automatique ; c'est-à-dire calculer le gradient d'un calcul par rapport à certaines entrées, généralement tf.Variable s. TensorFlow "enregistre" les opérations pertinentes exécutées dans le contexte d'un tf.GradientTape sur une "bande". TensorFlow utilise ensuite cette bande pour calculer les gradients d'un calcul "enregistré" en utilisant la différenciation en mode inverse .
Voici un exemple simple :
x = tf.Variable(3.0)
with tf.GradientTape() as tape:
y = x**2
Une fois que vous avez enregistré certaines opérations, utilisez GradientTape.gradient(target, sources) pour calculer le gradient d'une cible (souvent une perte) par rapport à une source (souvent les variables du modèle) :
# dy = 2x * dx
dy_dx = tape.gradient(y, x)
dy_dx.numpy()
6.0
L'exemple ci-dessus utilise des scalaires, mais tf.GradientTape fonctionne aussi facilement sur n'importe quel tenseur :
w = tf.Variable(tf.random.normal((3, 2)), name='w')
b = tf.Variable(tf.zeros(2, dtype=tf.float32), name='b')
x = [[1., 2., 3.]]
with tf.GradientTape(persistent=True) as tape:
y = x @ w + b
loss = tf.reduce_mean(y**2)
Pour obtenir le gradient de loss par rapport aux deux variables, vous pouvez passer les deux comme sources à la méthode du gradient . La bande est flexible sur la façon dont les sources sont transmises et acceptera toute combinaison imbriquée de listes ou de dictionnaires et renverra le dégradé structuré de la même manière (voir tf.nest ).
[dl_dw, dl_db] = tape.gradient(loss, [w, b])
Le gradient par rapport à chaque source a la forme de la source :
print(w.shape)
print(dl_dw.shape)
(3, 2) (3, 2)
Voici à nouveau le calcul du gradient, cette fois en passant un dictionnaire de variables :
my_vars = {
'w': w,
'b': b
}
grad = tape.gradient(loss, my_vars)
grad['b']
<tf.Tensor: shape=(2,), dtype=float32, numpy=array([-1.6920902, -3.2363236], dtype=float32)>
Gradients par rapport à un modèle
Il est courant de collecter tf.Variables dans un tf.Module ou l'une de ses sous-classes ( layers.Layer , keras.Model ) pour le contrôle et l'exportation .
Dans la plupart des cas, vous souhaiterez calculer des gradients par rapport aux variables entraînables d'un modèle. Étant donné que toutes les sous-classes de tf.Module agrègent leurs variables dans la propriété Module.trainable_variables , vous pouvez calculer ces gradients en quelques lignes de code :
layer = tf.keras.layers.Dense(2, activation='relu')
x = tf.constant([[1., 2., 3.]])
with tf.GradientTape() as tape:
# Forward pass
y = layer(x)
loss = tf.reduce_mean(y**2)
# Calculate gradients with respect to every trainable variable
grad = tape.gradient(loss, layer.trainable_variables)
for var, g in zip(layer.trainable_variables, grad):
print(f'{var.name}, shape: {g.shape}')
dense/kernel:0, shape: (3, 2) dense/bias:0, shape: (2,)
Contrôler ce que la bande regarde
Le comportement par défaut consiste à enregistrer toutes les opérations après avoir accédé à un tf.Variable . Les raisons en sont :
- La bande doit savoir quelles opérations enregistrer dans le passage avant pour calculer les gradients dans le passage arrière.
- La bande contient des références aux sorties intermédiaires, vous ne voulez donc pas enregistrer d'opérations inutiles.
- Le cas d'utilisation le plus courant consiste à calculer le gradient d'une perte par rapport à toutes les variables entraînables d'un modèle.
Par exemple, ce qui suit ne parvient pas à calculer un gradient car le tf.Tensor n'est pas "surveillé" par défaut et le tf.Variable ne peut pas être formé :
# A trainable variable
x0 = tf.Variable(3.0, name='x0')
# Not trainable
x1 = tf.Variable(3.0, name='x1', trainable=False)
# Not a Variable: A variable + tensor returns a tensor.
x2 = tf.Variable(2.0, name='x2') + 1.0
# Not a variable
x3 = tf.constant(3.0, name='x3')
with tf.GradientTape() as tape:
y = (x0**2) + (x1**2) + (x2**2)
grad = tape.gradient(y, [x0, x1, x2, x3])
for g in grad:
print(g)
tf.Tensor(6.0, shape=(), dtype=float32) None None None
Vous pouvez répertorier les variables surveillées par la bande à l'aide de la méthode GradientTape.watched_variables :
[var.name for var in tape.watched_variables()]
['x0:0']
tf.GradientTape fournit des hooks qui permettent à l'utilisateur de contrôler ce qui est ou non surveillé.
Pour enregistrer des gradients par rapport à un tf.Tensor , vous devez appeler GradientTape.watch(x) :
x = tf.constant(3.0)
with tf.GradientTape() as tape:
tape.watch(x)
y = x**2
# dy = 2x * dx
dy_dx = tape.gradient(y, x)
print(dy_dx.numpy())
6.0
Inversement, pour désactiver le comportement par défaut de surveillance de tous les tf.Variables , définissez watch_accessed_variables=False lors de la création de la bande de dégradé. Ce calcul utilise deux variables, mais ne connecte le gradient que pour l'une des variables :
x0 = tf.Variable(0.0)
x1 = tf.Variable(10.0)
with tf.GradientTape(watch_accessed_variables=False) as tape:
tape.watch(x1)
y0 = tf.math.sin(x0)
y1 = tf.nn.softplus(x1)
y = y0 + y1
ys = tf.reduce_sum(y)
Étant donné que GradientTape.watch n'a pas été appelé sur x0 , aucun gradient n'est calculé par rapport à celui-ci :
# dys/dx1 = exp(x1) / (1 + exp(x1)) = sigmoid(x1)
grad = tape.gradient(ys, {'x0': x0, 'x1': x1})
print('dy/dx0:', grad['x0'])
print('dy/dx1:', grad['x1'].numpy())
dy/dx0: None dy/dx1: 0.9999546
Résultats intermédiaires
Vous pouvez également demander des gradients de la sortie par rapport aux valeurs intermédiaires calculées dans le contexte tf.GradientTape .
x = tf.constant(3.0)
with tf.GradientTape() as tape:
tape.watch(x)
y = x * x
z = y * y
# Use the tape to compute the gradient of z with respect to the
# intermediate value y.
# dz_dy = 2 * y and y = x ** 2 = 9
print(tape.gradient(z, y).numpy())
18.0
Par défaut, les ressources détenues par un GradientTape sont libérées dès que la méthode GradientTape.gradient est appelée. Pour calculer plusieurs dégradés sur le même calcul, créez un ruban de dégradé avec persistent=True . Cela permet plusieurs appels à la méthode de gradient lorsque les ressources sont libérées lorsque l'objet bande est récupéré. Par example:
x = tf.constant([1, 3.0])
with tf.GradientTape(persistent=True) as tape:
tape.watch(x)
y = x * x
z = y * y
print(tape.gradient(z, x).numpy()) # [4.0, 108.0] (4 * x**3 at x = [1.0, 3.0])
print(tape.gradient(y, x).numpy()) # [2.0, 6.0] (2 * x at x = [1.0, 3.0])
[ 4. 108.] [2. 6.]
del tape # Drop the reference to the tape
Remarques sur les performances
Il y a une petite surcharge associée à l'exécution d'opérations dans un contexte de bande dégradée. Pour une exécution plus rapide, cela ne représentera pas un coût notable, mais vous devez toujours utiliser le contexte de bande dans les zones uniquement où cela est nécessaire.
Les bandes de gradient utilisent la mémoire pour stocker les résultats intermédiaires, y compris les entrées et les sorties, à utiliser lors du passage en arrière.
Pour plus d'efficacité, certaines ops (comme
ReLU) n'ont pas besoin de conserver leurs résultats intermédiaires et elles sont élaguées lors de la passe avant. Cependant, si vous utilisezpersistent=Truesur votre bande, rien n'est ignoré et votre utilisation maximale de la mémoire sera plus élevée.
Gradients des cibles non scalaires
Un gradient est fondamentalement une opération sur un scalaire.
x = tf.Variable(2.0)
with tf.GradientTape(persistent=True) as tape:
y0 = x**2
y1 = 1 / x
print(tape.gradient(y0, x).numpy())
print(tape.gradient(y1, x).numpy())
4.0 -0.25
Ainsi, si vous demandez le gradient de plusieurs cibles, le résultat pour chaque source est :
- Le gradient de la somme des cibles, ou de manière équivalente
- La somme des gradients de chaque cible.
x = tf.Variable(2.0)
with tf.GradientTape() as tape:
y0 = x**2
y1 = 1 / x
print(tape.gradient({'y0': y0, 'y1': y1}, x).numpy())
3.75
De même, si la ou les cibles ne sont pas scalaires, le gradient de la somme est calculé :
x = tf.Variable(2.)
with tf.GradientTape() as tape:
y = x * [3., 4.]
print(tape.gradient(y, x).numpy())
7.0
Cela permet de prendre simplement le gradient de la somme d'une collection de pertes, ou le gradient de la somme d'un calcul de perte élément par élément.
Si vous avez besoin d'un dégradé distinct pour chaque élément, reportez-vous aux Jacobiens .
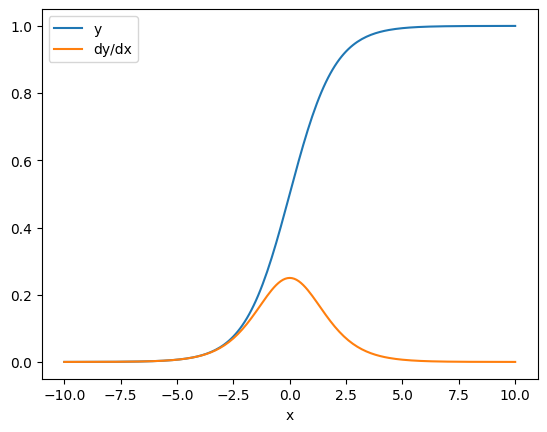
Dans certains cas, vous pouvez ignorer le jacobien. Pour un calcul élément par élément, le gradient de la somme donne la dérivée de chaque élément par rapport à son élément d'entrée, puisque chaque élément est indépendant :
x = tf.linspace(-10.0, 10.0, 200+1)
with tf.GradientTape() as tape:
tape.watch(x)
y = tf.nn.sigmoid(x)
dy_dx = tape.gradient(y, x)
plt.plot(x, y, label='y')
plt.plot(x, dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')
Flux de contrôle
Étant donné qu'une bande dégradée enregistre les opérations au fur et à mesure de leur exécution, le flux de contrôle Python est naturellement géré (par exemple, les instructions if et while ).
Ici, une variable différente est utilisée sur chaque branche d'un if . Le dégradé se connecte uniquement à la variable qui a été utilisée :
x = tf.constant(1.0)
v0 = tf.Variable(2.0)
v1 = tf.Variable(2.0)
with tf.GradientTape(persistent=True) as tape:
tape.watch(x)
if x > 0.0:
result = v0
else:
result = v1**2
dv0, dv1 = tape.gradient(result, [v0, v1])
print(dv0)
print(dv1)
tf.Tensor(1.0, shape=(), dtype=float32) None
N'oubliez pas que les instructions de contrôle elles-mêmes ne sont pas différentiables, elles sont donc invisibles pour les optimiseurs basés sur le gradient.
En fonction de la valeur de x dans l'exemple ci-dessus, la bande enregistre soit result = v0 soit result = v1**2 . Le gradient par rapport à x est toujours None .
dx = tape.gradient(result, x)
print(dx)
None
Obtenir un dégradé de None
Lorsqu'une cible n'est pas connectée à une source, vous obtenez un dégradé de None .
x = tf.Variable(2.)
y = tf.Variable(3.)
with tf.GradientTape() as tape:
z = y * y
print(tape.gradient(z, x))
None
Ici, z n'est évidemment pas connecté à x , mais il existe plusieurs façons moins évidentes de déconnecter un gradient.
1. Remplacement d'une variable par un tenseur
Dans la section "contrôler ce que la bande regarde" , vous avez vu que la bande regardera automatiquement un tf.Variable mais pas un tf.Tensor .
Une erreur courante consiste à remplacer par inadvertance un tf.Variable par un tf.Tensor , au lieu d'utiliser Variable.assign pour mettre à jour le tf.Variable . Voici un exemple:
x = tf.Variable(2.0)
for epoch in range(2):
with tf.GradientTape() as tape:
y = x+1
print(type(x).__name__, ":", tape.gradient(y, x))
x = x + 1 # This should be `x.assign_add(1)`
ResourceVariable : tf.Tensor(1.0, shape=(), dtype=float32) EagerTensor : None
2. A fait des calculs en dehors de TensorFlow
La bande ne peut pas enregistrer le chemin du dégradé si le calcul quitte TensorFlow. Par example:
x = tf.Variable([[1.0, 2.0],
[3.0, 4.0]], dtype=tf.float32)
with tf.GradientTape() as tape:
x2 = x**2
# This step is calculated with NumPy
y = np.mean(x2, axis=0)
# Like most ops, reduce_mean will cast the NumPy array to a constant tensor
# using `tf.convert_to_tensor`.
y = tf.reduce_mean(y, axis=0)
print(tape.gradient(y, x))
None
3. A pris des dégradés à travers un entier ou une chaîne
Les entiers et les chaînes ne sont pas différentiables. Si un chemin de calcul utilise ces types de données, il n'y aura pas de gradient.
Personne ne s'attend à ce que les chaînes soient différentiables, mais il est facile de créer accidentellement une constante ou une variable int si vous ne spécifiez pas le dtype .
x = tf.constant(10)
with tf.GradientTape() as g:
g.watch(x)
y = x * x
print(g.gradient(y, x))
WARNING:tensorflow:The dtype of the watched tensor must be floating (e.g. tf.float32), got tf.int32 WARNING:tensorflow:The dtype of the target tensor must be floating (e.g. tf.float32) when calling GradientTape.gradient, got tf.int32 WARNING:tensorflow:The dtype of the source tensor must be floating (e.g. tf.float32) when calling GradientTape.gradient, got tf.int32 None
TensorFlow n'effectue pas automatiquement de cast entre les types, donc, dans la pratique, vous obtiendrez souvent une erreur de type au lieu d'un dégradé manquant.
4. A pris des dégradés à travers un objet avec état
L'état arrête les gradients. Lorsque vous lisez à partir d'un objet avec état, la bande ne peut observer que l'état actuel, pas l'historique qui y conduit.
Un tf.Tensor est immuable. Vous ne pouvez pas modifier un tenseur une fois qu'il est créé. Il a une valeur , mais pas d' état . Toutes les opérations décrites jusqu'ici sont également sans état : la sortie d'un tf.matmul ne dépend que de ses entrées.
Un tf.Variable a un état interne — sa valeur. Lorsque vous utilisez la variable, l'état est lu. Il est normal de calculer un gradient par rapport à une variable, mais l'état de la variable empêche les calculs de gradient de remonter plus loin. Par example:
x0 = tf.Variable(3.0)
x1 = tf.Variable(0.0)
with tf.GradientTape() as tape:
# Update x1 = x1 + x0.
x1.assign_add(x0)
# The tape starts recording from x1.
y = x1**2 # y = (x1 + x0)**2
# This doesn't work.
print(tape.gradient(y, x0)) #dy/dx0 = 2*(x1 + x0)
None
De même, les itérateurs tf.data.Dataset et les tf.queue sont avec état et arrêteront tous les gradients sur les tenseurs qui les traversent.
Aucun dégradé enregistré
Certains tf.Operation s sont enregistrés comme étant non différentiables et renverront None . D'autres n'ont pas de gradient enregistré .
La page tf.raw_ops montre quelles opérations de bas niveau ont des gradients enregistrés.
Si vous essayez de faire passer un dégradé à travers une opération flottante qui n'a pas de dégradé enregistré, la bande générera une erreur au lieu de renvoyer silencieusement None . De cette façon, vous savez que quelque chose ne va pas.
Par exemple, la fonction tf.image.adjust_contrast enveloppe raw_ops.AdjustContrastv2 , qui pourrait avoir un dégradé mais le dégradé n'est pas implémenté :
image = tf.Variable([[[0.5, 0.0, 0.0]]])
delta = tf.Variable(0.1)
with tf.GradientTape() as tape:
new_image = tf.image.adjust_contrast(image, delta)
try:
print(tape.gradient(new_image, [image, delta]))
assert False # This should not happen.
except LookupError as e:
print(f'{type(e).__name__}: {e}')
LookupError: gradient registry has no entry for: AdjustContrastv2
Si vous avez besoin de vous différencier via cette opération, vous devrez soit implémenter le gradient et l'enregistrer (en utilisant tf.RegisterGradient ), soit réimplémenter la fonction en utilisant d'autres opérations.
Des zéros au lieu de Aucun
Dans certains cas, il serait pratique d'obtenir 0 au lieu de None pour les dégradés non connectés. Vous pouvez décider quoi renvoyer lorsque vous avez des dégradés non connectés à l'aide de l'argument unconnected_gradients :
x = tf.Variable([2., 2.])
y = tf.Variable(3.)
with tf.GradientTape() as tape:
z = y**2
print(tape.gradient(z, x, unconnected_gradients=tf.UnconnectedGradients.ZERO))
tf.Tensor([0. 0.], shape=(2,), dtype=float32)
