 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Przewodnik Wprowadzenie do gradientów i automatycznego różnicowania zawiera wszystko, co jest wymagane do obliczania gradientów w TensorFlow. Ten przewodnik koncentruje się na głębszych, mniej typowych funkcjach interfejsu API tf.GradientTape .
Ustawiać
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['figure.figsize'] = (8, 6)
Kontrolowanie nagrywania gradientu
W podręczniku automatycznego różnicowania zobaczyłeś, jak kontrolować, które zmienne i tensory są obserwowane przez taśmę podczas budowania obliczeń gradientu.
Taśma posiada również metody manipulacji nagraniem.
Zatrzymaj nagrywanie
Jeśli chcesz zatrzymać nagrywanie gradientów, możesz użyć tf.GradientTape.stop_recording , aby tymczasowo zawiesić nagrywanie.
Może to być przydatne w celu zmniejszenia narzutu, jeśli nie chcesz rozróżniać skomplikowanej operacji w środku modelu. Może to obejmować obliczenie metryki lub wyniku pośredniego:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
x_sq = x * x
with t.stop_recording():
y_sq = y * y
z = x_sq + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Zresetuj/rozpocznij nagrywanie od zera
Jeśli chcesz zacząć od nowa, użyj tf.GradientTape.reset . Proste wyjście z bloku taśmy gradientowej i ponowne uruchomienie jest zwykle łatwiejsze do odczytania, ale można użyć metody reset , gdy wyjście z bloku taśmy jest trudne lub niemożliwe.
x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True
with tf.GradientTape() as t:
y_sq = y * y
if reset:
# Throw out all the tape recorded so far.
t.reset()
z = x * x + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Zatrzymaj przepływ gradientu z precyzją
W przeciwieństwie do powyższych globalnych kontrolek taśm, funkcja tf.stop_gradient jest znacznie bardziej precyzyjna. Może być używany do zatrzymania gradientów płynących po określonej ścieżce, bez konieczności dostępu do samej taśmy:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
y_sq = y**2
z = x**2 + tf.stop_gradient(y_sq)
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Gradienty niestandardowe
W niektórych przypadkach możesz chcieć dokładnie kontrolować sposób obliczania gradientów, zamiast używać wartości domyślnych. Sytuacje te obejmują:
- Nie ma zdefiniowanego gradientu dla nowej operacji, którą piszesz.
- Obliczenia domyślne są numerycznie niestabilne.
- Chcesz buforować kosztowne obliczenia z przejścia w przód.
- Chcesz zmodyfikować wartość (na przykład używając
tf.clip_by_valuelubtf.math.round) bez modyfikowania gradientu.
W pierwszym przypadku, aby napisać nową operację, możesz użyć tf.RegisterGradient , aby skonfigurować własną (szczegóły znajdziesz w dokumentacji API). (Pamiętaj, że rejestr gradientów jest globalny, więc zmieniaj go ostrożnie).
W ostatnich trzech przypadkach możesz użyć tf.custom_gradient .
Oto przykład, który stosuje tf.clip_by_norm do gradientu pośredniego:
# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
def backward(dy):
return tf.clip_by_norm(dy, 0.5)
return y, backward
v = tf.Variable(2.0)
with tf.GradientTape() as t:
output = clip_gradients(v * v)
print(t.gradient(output, v)) # calls "backward", which clips 4 to 2
tf.Tensor(2.0, shape=(), dtype=float32)
Więcej informacji można znaleźć w dokumentacji interfejsu API dekoratora tf.custom_gradient .
Gradienty niestandardowe w SavedModel
Niestandardowe gradienty można zapisać w SavedModel za pomocą opcji tf.saved_model.SaveOptions(experimental_custom_gradients=True) .
Aby została zapisana w SavedModel, funkcja gradientu musi być identyfikowalna (aby dowiedzieć się więcej, zapoznaj się z przewodnikiem Lepsza wydajność z tf.function ).
class MyModule(tf.Module):
@tf.function(input_signature=[tf.TensorSpec(None)])
def call_custom_grad(self, x):
return clip_gradients(x)
model = MyModule()
tf.saved_model.save(
model,
'saved_model',
options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))
# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))
INFO:tensorflow:Assets written to: saved_model/assets tf.Tensor(2.0, shape=(), dtype=float32)
Uwaga na temat powyższego przykładu: jeśli spróbujesz zastąpić powyższy kod kodem tf.saved_model.SaveOptions(experimental_custom_gradients=False) , gradient będzie nadal dawał ten sam wynik podczas ładowania. Powodem jest to, że rejestr gradientów nadal zawiera niestandardowy gradient używany w funkcji call_custom_op . Jeśli jednak środowisko wykonawcze zostanie ponownie uruchomione po zapisaniu bez gradientów niestandardowych, uruchomienie załadowanego modelu pod tf.GradientTape spowoduje wyświetlenie błędu: LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN) .
Wiele taśm
Wiele taśm współpracuje bezproblemowo.
Na przykład tutaj każda taśma ogląda inny zestaw tensorów:
x0 = tf.constant(0.0)
x1 = tf.constant(0.0)
with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
tape0.watch(x0)
tape1.watch(x1)
y0 = tf.math.sin(x0)
y1 = tf.nn.sigmoid(x1)
y = y0 + y1
ys = tf.reduce_sum(y)
tape0.gradient(ys, x0).numpy() # cos(x) => 1.0
1.0
tape1.gradient(ys, x1).numpy() # sigmoid(x1)*(1-sigmoid(x1)) => 0.25
0.25
Gradienty wyższego rzędu
Operacje wewnątrz menedżera kontekstu tf.GradientTape są rejestrowane w celu automatycznego rozróżniania. Jeśli gradienty są obliczane w tym kontekście, obliczanie gradientu jest również rejestrowane. W rezultacie dokładnie to samo API działa również dla gradientów wyższego rzędu.
Na przykład:
x = tf.Variable(1.0) # Create a Tensorflow variable initialized to 1.0
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = x * x * x
# Compute the gradient inside the outer `t2` context manager
# which means the gradient computation is differentiable as well.
dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)
print('dy_dx:', dy_dx.numpy()) # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy()) # 6 * x => 6.0
dy_dx: 3.0 d2y_dx2: 6.0
Chociaż daje to drugą pochodną funkcji skalarnej , ten wzorzec nie uogólnia, aby utworzyć macierz Hessian, ponieważ tf.GradientTape.gradient oblicza tylko gradient skalarny. Aby skonstruować macierz heską , przejdź do przykładu heskiego w sekcji jakobian .
„Zagnieżdżone wywołania tf.GradientTape.gradient ” to dobry wzorzec, gdy obliczasz skalar z gradientu, a wynikowy skalar działa jako źródło dla drugiego obliczenia gradientu, jak w poniższym przykładzie.
Przykład: regularyzacja gradientu wejściowego
Wiele modeli jest podatnych na „przykłady kontradyktoryjne”. Ten zbiór technik modyfikuje dane wejściowe modelu, aby pomylić dane wyjściowe modelu. Najprostsza implementacja — taka jak przykład Adversarial wykorzystujący atak Fast Gradient Signed Method — wykonuje pojedynczy krok wzdłuż gradientu danych wyjściowych w odniesieniu do danych wejściowych; „gradient wejściowy”.
Jedną z technik zwiększania odporności na przeciwstawne przykłady jest regularyzacja gradientu wejściowego (Finlay i Oberman, 2019), która próbuje zminimalizować wielkość gradientu wejściowego. Jeśli gradient wejściowy jest mały, to zmiana wyjścia również powinna być niewielka.
Poniżej znajduje się naiwna implementacja regularyzacji gradientu wejściowego. Realizacja to:
- Oblicz gradient wyjścia w stosunku do wejścia za pomocą wewnętrznej taśmy.
- Oblicz wielkość tego gradientu wejściowego.
- Oblicz gradient tej wielkości w odniesieniu do modelu.
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape() as t2:
# The inner tape only takes the gradient with respect to the input,
# not the variables.
with tf.GradientTape(watch_accessed_variables=False) as t1:
t1.watch(x)
y = layer(x)
out = tf.reduce_sum(layer(x)**2)
# 1. Calculate the input gradient.
g1 = t1.gradient(out, x)
# 2. Calculate the magnitude of the input gradient.
g1_mag = tf.norm(g1)
# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)
[var.shape for var in dg1_mag]
[TensorShape([5, 10]), TensorShape([10])]
Jakobian
We wszystkich poprzednich przykładach wzięto gradienty celu skalarnego w odniesieniu do niektórych tensorów źródłowych.
Macierz Jakobian reprezentuje gradienty funkcji o wartościach wektorowych. Każdy wiersz zawiera gradient jednego z elementów wektora.
Metoda tf.GradientTape.jacobian pozwala na wydajne obliczenie macierzy jakobianu.
Zwróć uwagę, że:
- Jak
gradient: argumentsourcesmoże być tensorem lub kontenerem tensorów. - W przeciwieństwie do
gradient: Tensortargetmusi być pojedynczym tensorem.
Źródło skalarne
Jako pierwszy przykład, oto jakobian celu wektorowego w odniesieniu do źródła skalarnego.
x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)
with tf.GradientTape() as tape:
y = tf.nn.sigmoid(x+delta)
dy_dx = tape.jacobian(y, delta)
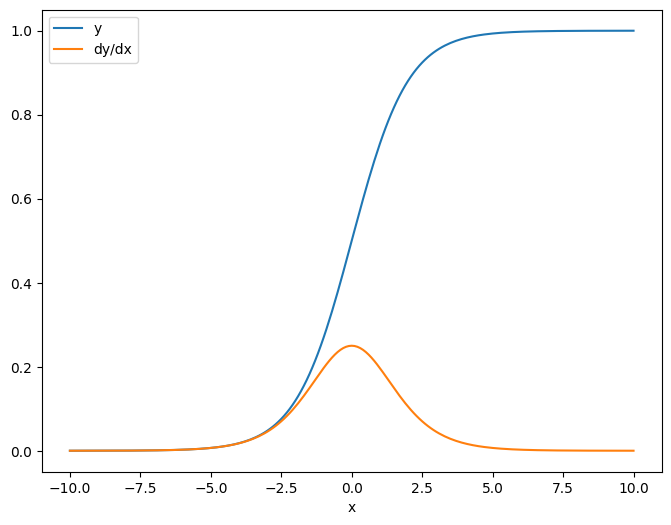
Kiedy weźmiesz jakobian w odniesieniu do skalara, wynik ma kształt celu i daje gradient każdego elementu w odniesieniu do źródła:
print(y.shape)
print(dy_dx.shape)
(201,) (201,)
plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')
Źródło tensora
Niezależnie od tego, czy dane wejściowe są skalarne, czy tensorowe, tf.GradientTape.jacobian skutecznie oblicza gradient każdego elementu źródła w odniesieniu do każdego elementu celu(ów).
Na przykład wyjście tej warstwy ma kształt (10, 7) :
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape(persistent=True) as tape:
y = layer(x)
y.shape
TensorShape([7, 10])
A kształt jądra warstwy to (5, 10) :
layer.kernel.shape
TensorShape([5, 10])
Kształt jakobianu wyjścia w odniesieniu do jądra to te dwa połączone ze sobą kształty:
j = tape.jacobian(y, layer.kernel)
j.shape
TensorShape([7, 10, 5, 10])
Jeśli sumujesz wymiary celu, pozostajesz z gradientem sumy, która zostałaby obliczona przez tf.GradientTape.gradient :
g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)
j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)
g.shape: (5, 10) delta: 2.3841858e-07
Przykład: Heski
Chociaż tf.GradientTape nie podaje wyraźnej metody konstruowania macierzy heskiej , możliwe jest jej zbudowanie przy użyciu metody tf.GradientTape.jacobian .
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
x = layer1(x)
x = layer2(x)
loss = tf.reduce_mean(x**2)
g = t1.gradient(loss, layer1.kernel)
h = t2.jacobian(g, layer1.kernel)
print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')
layer.kernel.shape: (5, 8) h.shape: (5, 8, 5, 8)
Aby użyć tego hesjanu w kroku metody Newtona , najpierw spłaszczysz jego osie w macierz, a gradient w wektor:
n_params = tf.reduce_prod(layer1.kernel.shape)
g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])
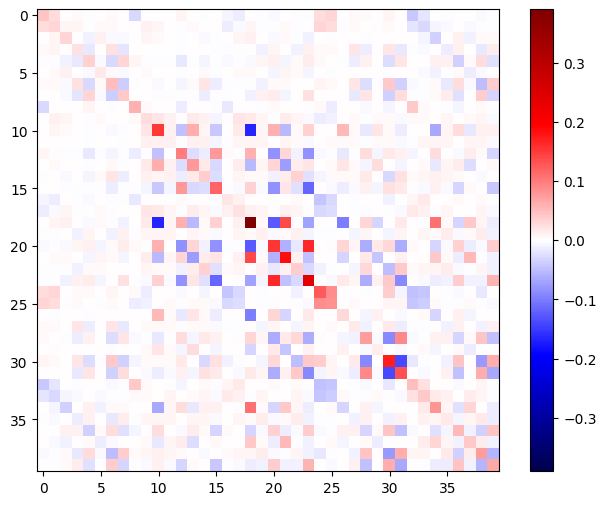
Macierz Hesja powinna być symetryczna:
def imshow_zero_center(image, **kwargs):
lim = tf.reduce_max(abs(image))
plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
plt.colorbar()
imshow_zero_center(h_mat)
Krok aktualizacji metody Newtona pokazano poniżej:
eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps
# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)
# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))
Chociaż jest to stosunkowo proste dla pojedynczej tf.Variable , zastosowanie tego do nietrywialnego modelu wymagałoby starannego łączenia i krojenia w celu uzyskania pełnego hesjanu dla wielu zmiennych.
Partia Jakobian
W niektórych przypadkach chcesz wziąć jakobian każdego ze stosu celów w odniesieniu do stosu źródeł, gdzie jakobiany dla każdej pary cel-źródło są niezależne.
Na przykład tutaj ma kształt wejściowy x (batch, ins) i kształt wyjściowy y (batch, outs) :
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = layer2(y)
y.shape
TensorShape([7, 6])
Pełny jakobian y względem x ma kształt (batch, ins, batch, outs) , nawet jeśli chcesz tylko (batch, ins, outs) :
j = tape.jacobian(y, x)
j.shape
TensorShape([7, 6, 7, 5])
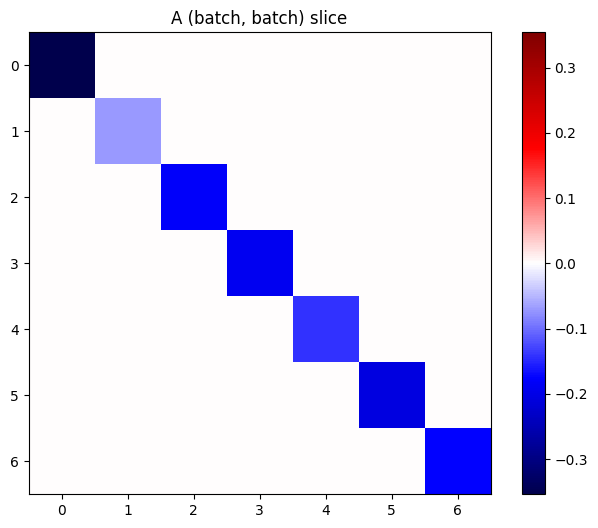
Jeżeli gradienty każdego elementu w stosie są niezależne, to każdy wycinek (batch, batch) tego tensora jest macierzą diagonalną:
imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')
def plot_as_patches(j):
# Reorder axes so the diagonals will each form a contiguous patch.
j = tf.transpose(j, [1, 0, 3, 2])
# Pad in between each patch.
lim = tf.reduce_max(abs(j))
j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
constant_values=-lim)
# Reshape to form a single image.
s = j.shape
j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])
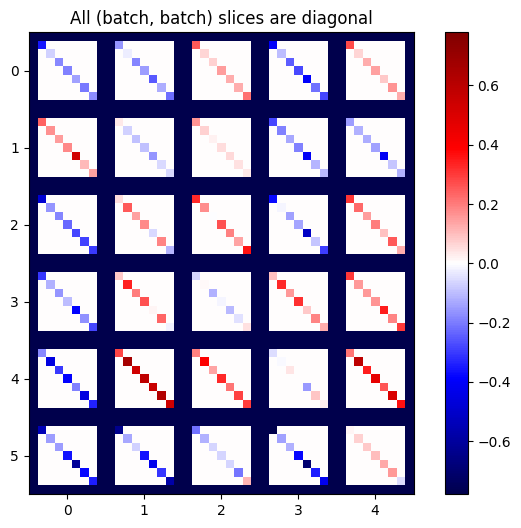
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')
Aby uzyskać pożądany wynik, możesz zsumować zduplikowany wymiar batch lub wybrać przekątne za pomocą tf.einsum :
j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)
(7, 6, 5) (7, 6, 5)
O wiele bardziej efektywne byłoby wykonanie obliczeń bez dodatkowego wymiaru. Metoda tf.GradientTape.batch_jacobian robi dokładnie to:
jb = tape.batch_jacobian(y, x)
jb.shape
WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f7d601250e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. TensorShape([7, 6, 5])
error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())
0.0
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = bn(y, training=True)
y = layer2(y)
j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')
WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f7cf062fa70> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. j.shape: (7, 6, 7, 5)
plot_as_patches(j)
_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")
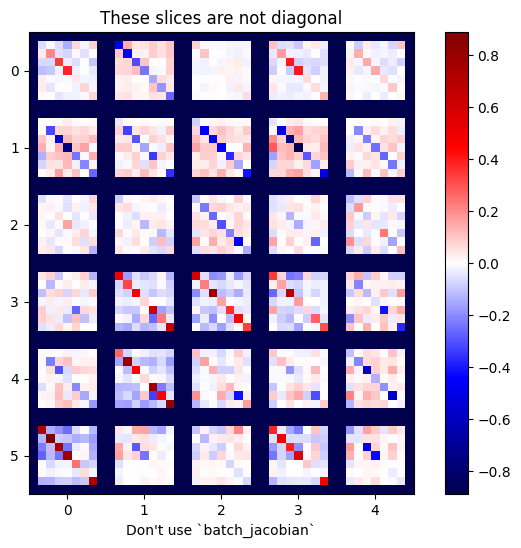
W tym przypadku batch_jacobian nadal działa i zwraca coś o oczekiwanym kształcie, ale jego zawartość ma niejasne znaczenie:
jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')
jb.shape: (7, 6, 5)
